基于分布式ICA-PCA模型的工业过程故障监测

衷路生，何东，龚锦红，张永贤

（华东交通大学电气学院，江西 南昌 330013）

基于分布式ICA-PCA模型的工业过程故障监测

衷路生，何东，龚锦红，张永贤

（华东交通大学电气学院，江西 南昌 330013）

提出基于分布式ICA-PCA( independent component analysis-principal component analysis)模型的工业过程故障监测方法，适合于复杂工业过程难以自动划分子块及过程数据存在非高斯信息的情况。首先，对过程数据进行PCA分解，并在PCA主成分不同的方向上构建不同的子块，把原始特征空间自动划分为不同子空间。然后，对各个子块采用ICA-PCA两步信息提取的策略，提取出高斯信息和非高斯信息，并构建新的统计量和统计限。最后，通过Tennessee Eastman(TE)过程的仿真实验，验证所提出故障监测模型的有效性和可行性。

复杂工业过程；自动划分子块；非高斯；ICA-PCA；故障监测

独立主元分析（ICA）由于能有效处理非高斯信息而广泛应用在过程监测领域。Lee等[10]提出使用ICA进行统计过程监测，同时，国内学者陈国金等[11]也对此做了很多工作；而后，Lee等[12]提出动态ICA的过程监测方法；Yoo等[13]指出可使用多路ICA进行在线过程监测；最近，Ge等[14]结合集成学习算法和贝叶斯推理策略提高了ICA的监测能力；Kano等[15]首次将ICA和PCA结合在一起，将数据分为高斯部分和非高斯部分；此后，Ge等[16]提出基于ICA-PCA两步信息提取的故障监测方法。

针对工业系统的复杂性，研究人员提出分层和分区统计的思想。MacGregor等[17]提出建立各个子块监测诊断图和全体监测图，提高监测性能；Westerhuis等[18]从算法和理论角度分析了多嵌段和多层次PCA、PLS算法，指出对同一个工业过程，其结果可以用普通PCA和PLS算法计算；Cherry 等[19]在讨论多嵌段PLS算法时，给出了子块和变量对T2及SPE贡献的新定义；Ge等[20]提出两步多嵌段监测方法。显然，这些方法都是利用过程知识来划分子块，而复杂工业过程的知识通常难以获得。因此，它们虽然提高了每个子块的监测能力，却无法满足自动划分子块的要求[21-22]。

基于以上分析，本文结合ICA理论提出分布式ICA-PCA模型，适合于复杂工业过程难以自动划分子块及过程数据存在非高斯信息的情况。首先，对过程数据进行PCA分解，获得各自含有不重叠信息的主元，在各个主元子空间和残差子空间上构建子块；其次，利用过程变量对各个子块的贡献值选择变量，构建互不相关的子块空间；最后，利用ICA算法提取各个子块的非高斯信息，对其残差进行PCA分解，构建统计量和统计限实现工业过程监测。

1　独立成分分析（ICA）

1.1ICA基本原理

ICA是伴随着盲分离问题而发展起来的一种统计信号处理方法，处理对象是相互统计独立的源信号经线性组合而产生的一组混合信号，目的是确定一个线性变换矩阵，使得混合信号变换后的输出分量尽可能地统计独立。假设有l个测量变量，在样本点k处，可以表示为r个未知独立成分[s1, s2,…,sr]T的线性组合，其中r≤l ；它们的关系如下所示[10]

ICA算法的基本原理就是在X已知的情况下，估计源信号矩阵S和混合矩阵A，其主要目的就是寻找一个分离矩阵W，可从观测信号中分离出源信号，即

1.2独立成分的排序和数目选取

对过程数据独立成分分析时，若独立成分数目选取过多，则会放大过程数据的噪声，反之，则难以有效提取数据的非高斯信息。为了选取合适的独立成分，本文首先根据分离矩阵 W每一行iw的欧几里得范数对信号的贡献大小来实现独立成分的排序，然后借鉴 PCA方差贡献图的原理，绘制iw的欧几里得范数对W的贡献图，采用试凑法来选取独立成分数目[10]。

2　基于分布式 ICA-PCA模型的过程监测

本节首先利用离线正常数据建立分布式ICA-PCA的故障监测模型；其次，对于新的测试样本，进行在线监测；最后，实现故障诊断。

2.1过程数据的子块划分和模型建立

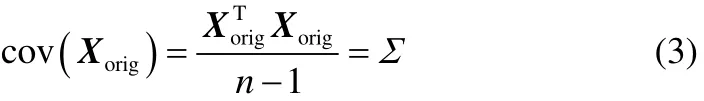
其中，origX已作归一化处理，即均值为0，标准差为1。如果选择k个主成分构建PCA模型，那么原始数据矩阵origX可以表示为it、ip和残差 E的和

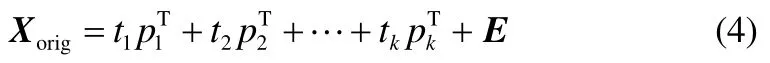
其中，it是得分向量，ip是载荷向量。式（4）可等价表示为

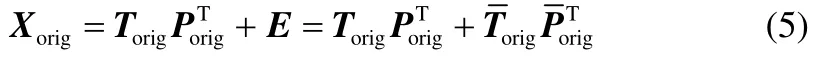
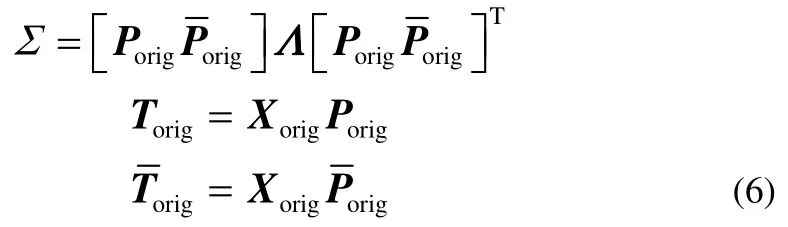
由于 PCA是在最小均方意义下寻找最能代表原始数据的投影方向，那么选择的k个主成分彼此是不相关的。通过在每一个不相关的主成分上构建子块，可以满足子块划分的多样性要求；在每一个不相关的子块上选择最相关的变量，可以满足每一个子块模型的精度要求。PCA模型的残差部分与每一个主成分都不相关，因此可在残差子空间构建一个子块。即在过程数据中，共构建k+1个子块。根据每个变量对各个主成分即各个子块的贡献值大小来选择各子块相应的变量[22]，具体地，所有变量对前k个子块的贡献值为

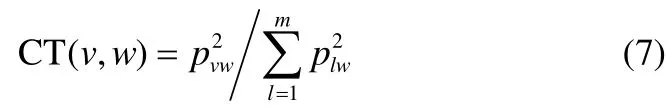
其中，v=1,2,…,m ，m为过程变量的数目；w=1,2,…,k，k为主成分数目；p为主元载荷矩阵，pvw表示该载荷矩阵在第v行、第w列的元素。

每个变量在残差载荷矩阵所有主元上的平均值为

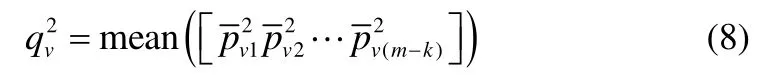
由式（8）可得所有变量对第k+1个子块的贡献值为

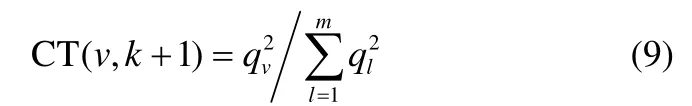
其中，v=1,2,…,m ，m为过程变量的数目；k为主成分数目，mean表示求均值。

根据式（7）、式（9），对各个子块贡献大的变量分别选作该子块的变量。

根据以上构建的子块，对每个单独子块构建分布式ICA-PCA模型。

首先，对每个单独子块Xi进行独立成分分析，设共提取出 ri个独立成分，则

源信号矩阵iS的估计值为

然后，对每个子块的残差矩阵Ei进行PCA分解

其中，i=1,2,…,k+1，Ti为每个子块的得分矩阵， Pi为每个子块的载荷矩阵， Fi为每个子块的残差矩阵。

本文通过检测各子块负熵值选择独立成分的数目：如果当前子块的负熵值为零或接近为零，说明子块过程数据的非高斯信息提取完全；主成分的数目可以由累计方差百分比规则（CPV）确定。

2.2基于分布式ICA-PCA模型的在线过程监测

对于一个新的数据样本 Z，计算每个子块的独立成分矩阵、得分矩阵如下

其中，i=1,2,…,k+1。

构建新的统计量I2、T2和SPE[10,16]。

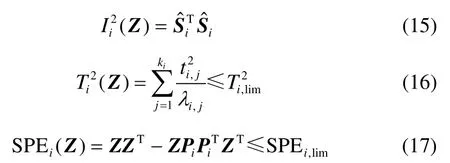
其中，i=1,2,…,k+1，ki为每个子块选取的主成分数目，λi, j为每个子块的特征值。

利用一维核密度估计（KDE）的方法求子块 I2的统计限[10-11]，定义如下

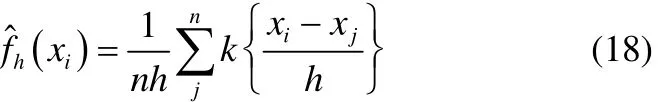
其中，i=1,2,…,k+1， xi为子块过程数据，h为窗宽或光滑参数，n为各子块样本数目，k为核函数。根据概率理论，核函数满足以下条件

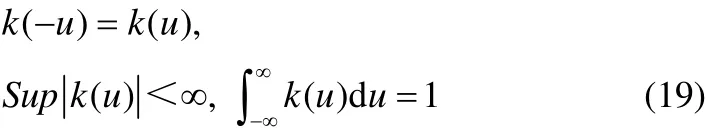
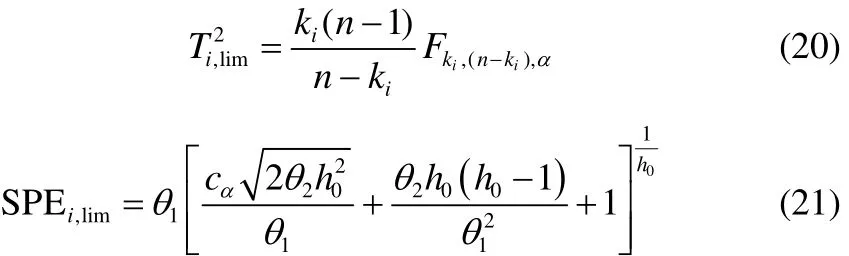
如果各个子块监测图的统计量超出了统计限，那么说明该子块发生了故障。

2.3故障诊断

为了确定引起故障的变量，借鉴文献[22]的思想，采用以下的故障诊断方法。

首先，把所有子块划分为两部分：可监测到故障的子块集合（FY）和无法监测到故障的子块集合（FN）。具体定义如下

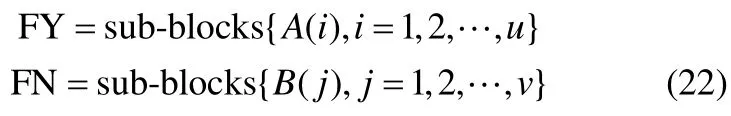
其中，u代表可监测到故障的子块数目，v代表无法监测到故障的子块数目，且u+v=k+1，A和B表示相应子块集合中所包含变量的向量。

其次，求出可监测到故障的子块所含变量的交集IVS（included variable set）和无法监测到故障的子块所含变量的交集EVS（excluded variable set），具体定义为

其中，J表示求所有子块变量的交集。

最后，通过整合IVS和EVS两个变量集合，可求得该故障的责任变量集合（responsible variable set，RVS），即

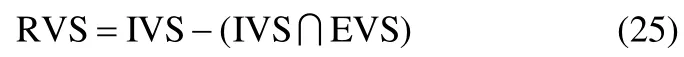
2.4监测模型效率分析

由于采集原始数据和故障测试数据的复杂性相同，因此本文从定性角度分析分布式 ICA-PCA故障监测模型的效率问题。在分布式PCA模型中，首先通过 PCA分解划分子块并求出可监测到故障的子块，然后在该子块构建传统PCA监测模型。而分布式ICA-PCA模型是在分布式PCA模型的基础上，增加了ICA的计算，即式（10）和式（11），因此分布式 ICA-PCA模型的效率稍慢。相比于ICA-PCA故障监测模型，由于分布式ICA-PCA模型已确定引起故障的子块，即建模矩阵和测试矩阵的维数大大降低，所以分布式 ICA-PCA模型的效率快于ICA-PCA模型。

2.5基于分布式ICA-PCA模型的故障诊断算法

综合2.1节、2.2节、2.3节的分析，得到分布式ICA-PCA模型的故障诊断算法，其中，步骤（1）～（3）为离线建模阶段，步骤（4）～（8）为在线监测阶段，具体为：

（1）获取正常数据，并进行归一化处理，构成建模数据库；

（2）对正常数据进行原始PCA分解，运用CPV准则提取 k个主成分，把过程数据划分为k+1个子块；

（3）对每个子块首先进行独立成分分析，获取分离矩阵Wi，并对其残差矩阵Ei进行PCA分解，获取载荷矩阵Pi；

（4）对于新的样本数据，同样进行归一化处理；

（5）计算每个子块新的独立成分矩阵 Sˆi和得分矩阵 ti；

（6）根据式（15）～式（21）计算每个子块的I2、T2和SPE统计量及其对应的统计限；

（7）根据故障监测的结果，把子块划分为两类：可监测到故障和无法监测到故障；

（8）利用式（25）求出引起该故障的变量，实现故障诊断。

3　TE过程仿真研究

为了说明所提出方法的性能，本节通过TE过程进行分布式 ICA-PCA、传统 PCA、文献[16]的ICA-PCA和文献[22]的分布式 PCA的对比仿真实验。

Tennessee Eastman（TE）仿真平台是美国Eastman化学公司根据实际化工反应过程开发的，该平台是一个开放的、具有挑战性的化工模型仿真平台[21,23]。整个过程包括以下5个主要单元：冷凝器、反应器、分离器、压缩机和汽提塔。TE过程的流程如图1所示。

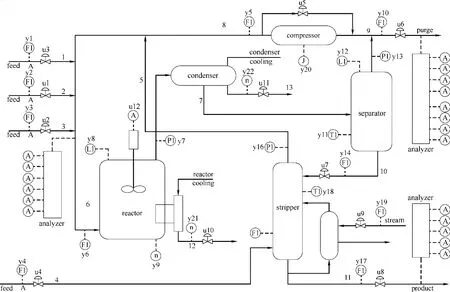
图1　TE平台流程Fig.1　TE benchmark process

TE过程包括12个操作变量和41个测量[21,23]，借鉴文献[10,16]的分析，本文选择了 33个变量，其中包括 11个操作变量，22个测量变量。采集过程平稳运行时的 960个数据作为训练样本，模拟故障工况时，采集 21种故障运行时的 960个样本，故障均在样本点161时引入。本文选用包含 960个样本的正常和故障数据集，来源于网站http://depts.washington.edu/control/LARRY/TE/down load.html。

根据CPV准则，对原始数据选择14个主成分进行传统 PCA分解，建立 15个子块的分布式ICA-PCA监测模型，通过检测各个子块的负熵值是否为零或接近零来选择独立成分数目，利用CPV准则确定子块的主成分数目，所有统计限的置信度均为95%。15个子块选择的主成分数目和独立成分数目如表1所示。

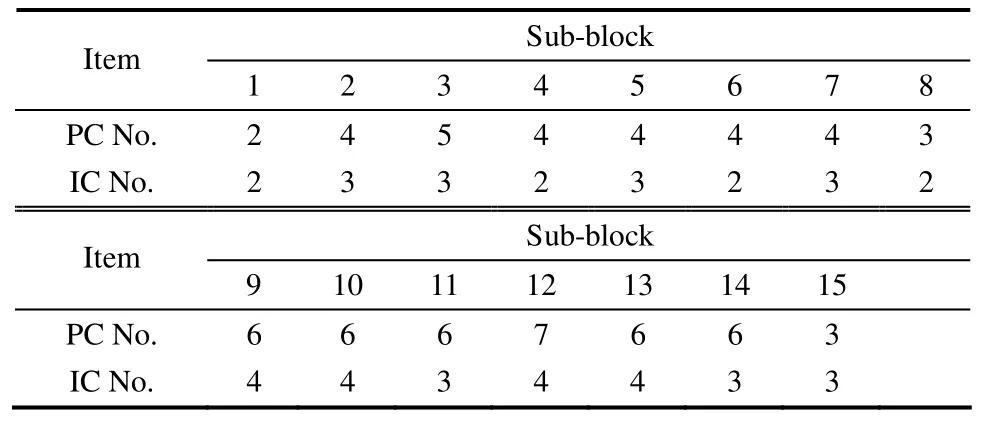
表1　子块主成分和独立成分数目Table 1　Selected PC and IC number in each sub-block

分别采用本文方法、传统PCA方法、ICA-PCA方法、分布式PCA方法进行对比仿真实验，其中，传统PCA和ICA-PCA方法的数据来自于文献[16]，分布式PCA方法的结果来源于文献[22]。4种方法对于21种故障的漏报率如表2所示，黑体表示同一故障漏报率的最小值。由表2可知，本文的分布式ICA-PCA方法对 TE过程监测的改进效果是明显的，即监测精度明显提高，特别对于故障1～4，8～11，15～21，漏报率明显低于另外3种方法。

引起故障5的原因是冷凝器冷却水入口温度阶跃变化，在此模式下，从冷凝器到分离器的出口流量也会增加，导致分离器温度和分离器冷却水出口温度升高。由于控制回路温度补偿的作用，约10 h后会再次达到稳态。文献[16]中PCA模型的监测结果如图2所示，从图2可知： T2、SPE统计量能够监测到第161～350样本点的故障，但对于350样本点之后的故障漏报率高，容易引起操作人员的误判。实际上，在故障5模式下，350样本点之后的压缩机冷却水的进口温度依然高于其设定值[16]。

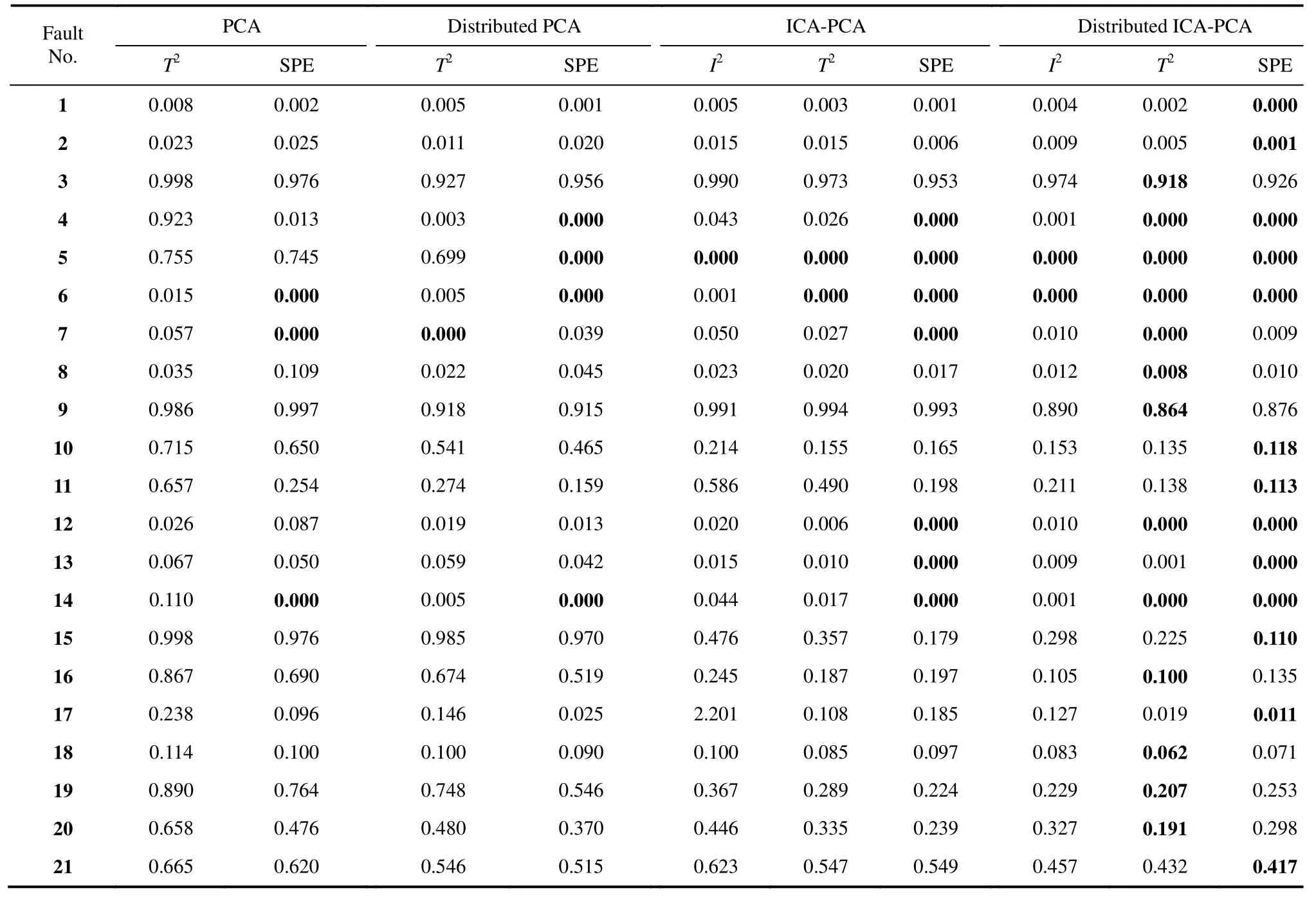
表2　TE过程中故障数据集的漏报率Table 2　Miss alarm rate of fault database in TE process

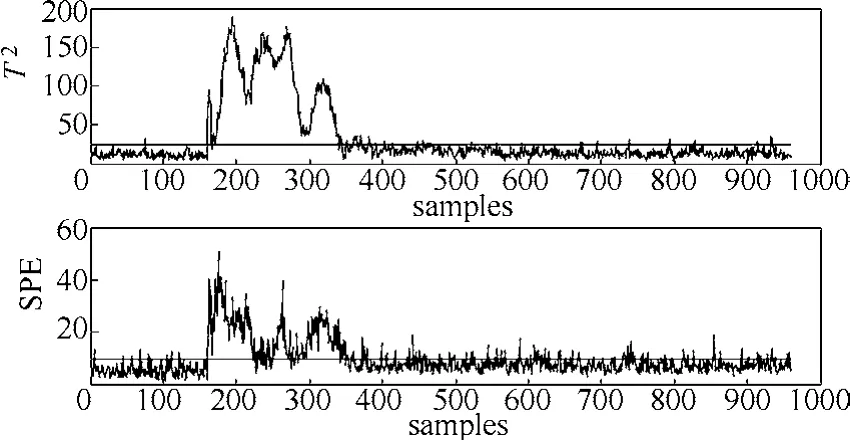
图2　故障5的PCA监测结果Fig.2　Monitoring results of fault 5 by PCA

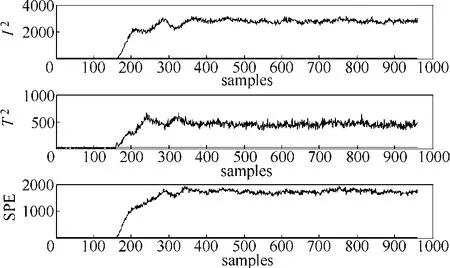
图3　故障5的ICA-PCA监测结果Fig.3　Monitoring results of fault 5 by ICA-PCA

文献[16]中ICA-PCA监测模型的结果如图3所示，可以看出，其达到很好的监测效果，且从表 2可知， I2、T2和SPE统计量的漏报率均为零，但由于其建模的全局性，ICA-PCA模型对大型复杂工艺流程监测效果不理想，且不能实时诊断出引起故障的因素。在文献[22]的分布式PCA监测模型中，对比各个子块监测图发现，只有子块4和子块6监测到故障。由图4可知，子块4和子块6均包括变量15（解析塔液位）、变量17（汽提塔底部流量）、变量30（汽提塔液体产品流量）和变量33（冷凝器冷却水流量），且其他子块不包括这些变量。因此，变量15、变量17、变量30和变量33为引起故障5的主要原因。以子块4和子块6为研究对象，其分布式PCA监测结果如图5所示，由图5可知：分布式PCA监测模型子块4、子块6的SPE统计量在故障发生后一直处于报警状态，但其 T2统计量在第350样本点后不能监测到故障。图6是本文的分布式ICA-PCA模型监测结果，从图6可得：分布式ICA-PCA模型子块4和子块6的I2、T2和SPE 3个统计量在故障发生后均处于报警状态，3个统计量的幅值大，结合表2可知，3个统计量平均漏报率均为零。

表3列出了4种方法对故障5和故障10的监测时间，结合表2故障5的漏报率说明：对于故障5，分布式ICA-PCA监测模型与ICA-PCA监测模型相比，其在精确监测到故障的同时，并没有牺牲系统的监测效率；与分布式PCA模型和PCA模型相比，虽然监测效率稍慢，但漏报率明显降低。

图4　两个子块的变量贡献图Fig.4　Variable contributions in two sub-blocks

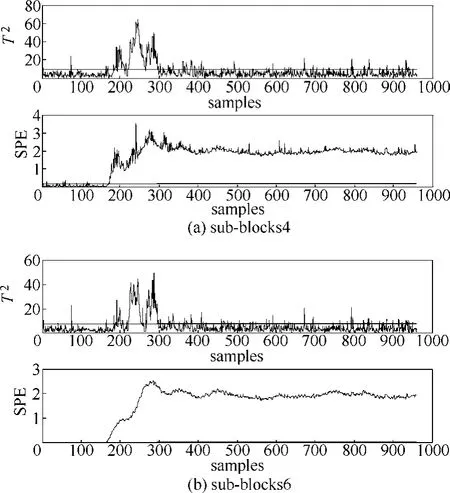
图5　故障5的分布式PCA监测结果Fig.5　Monitoring results of fault 5 by distributed PCA

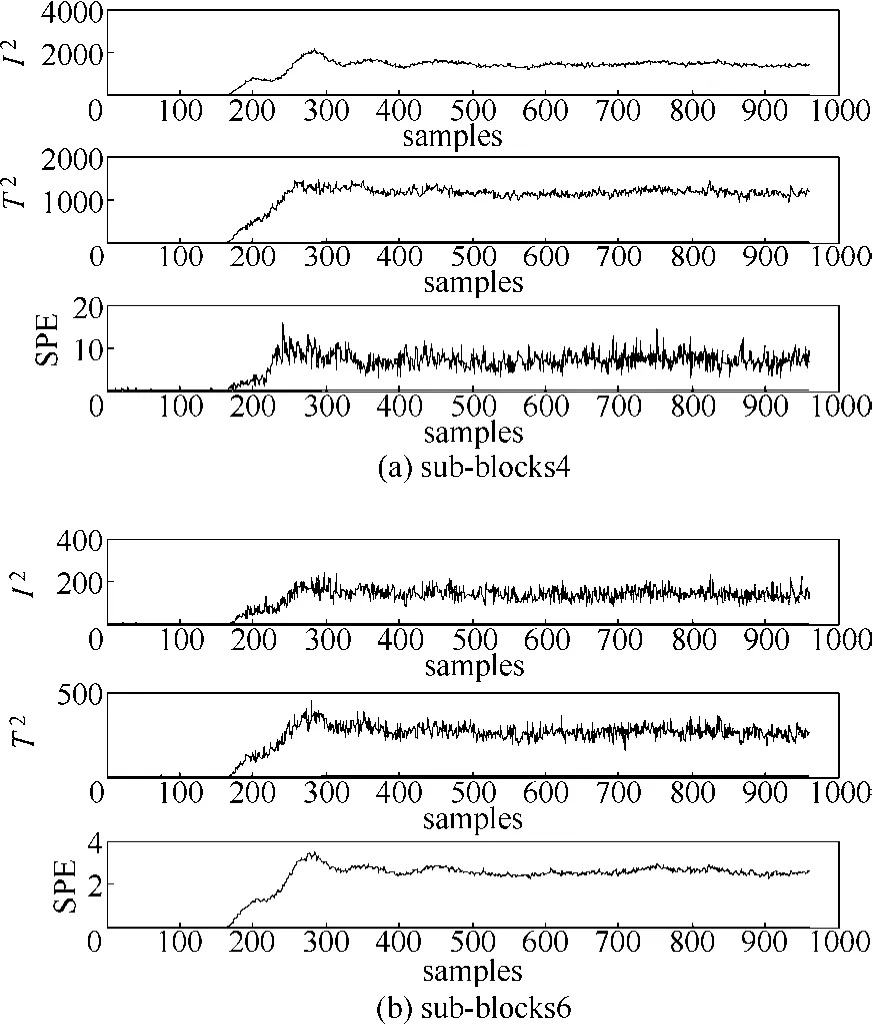
图6　故障5的分布式ICA-PCA监测结果Fig.6　Monitoring results of fault 5 by distributed ICA-PCA

表3　故障5的监测时间Table 3　Monitoring time of fault 5/s

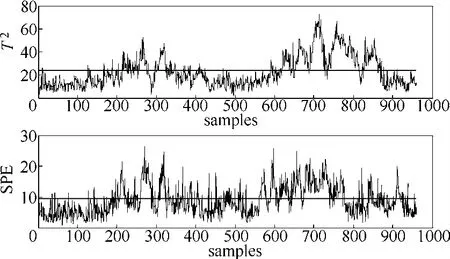
图7　故障10的PCA监测结果Fig.7　Monitoring results of fault 10 by PCA

引起故障10的原因是物料C的温度发生随机变化，文献[22]中PCA模型的监测结果如图7所示，根据表2，PCA模型对于故障10的故障漏报率高。图8为文献[16]的ICA-PCA模型监测结果，相比于图7，ICA-PCA模型提高了监测性能。由表2可知，ICA-PCA方法与PCA相比漏报率更低，但由于其建模的局限性，仍存在一定的漏报。在文献[22]分布式PCA监测模型中，对比15个子块的监测效果发现，仅子块1、子块2和子块15能够很好地监测故障。分析图9子块1、子块2和子块15的变量贡献图，3个子块均包括变量18（汽提塔温度）、变量19（汽提塔上部蒸汽流量）和变量27（压缩机再循环阀），且其他子块不包含这3个变量，因此，变量18、19和27是引起故障10的主要原因。图10是子块1、子块2和子块15的分布式PCA监测图。分布式ICA-PCA模型对于故障10的监测结果如图11所示，与图10、图8和图7相比，图11提高了监测性能。根据表2中4种方法对于故障10的漏报率可知，分布式ICA-PCA模型3个统计量的漏报率的均值小（最小值为0.118），说明相较于其他3种方法，本文方法对于故障10的监测精确性更高。

图8　故障10的ICA-PCA监测结果Fig.8　Monitoring results of fault 10 by ICA-PCA

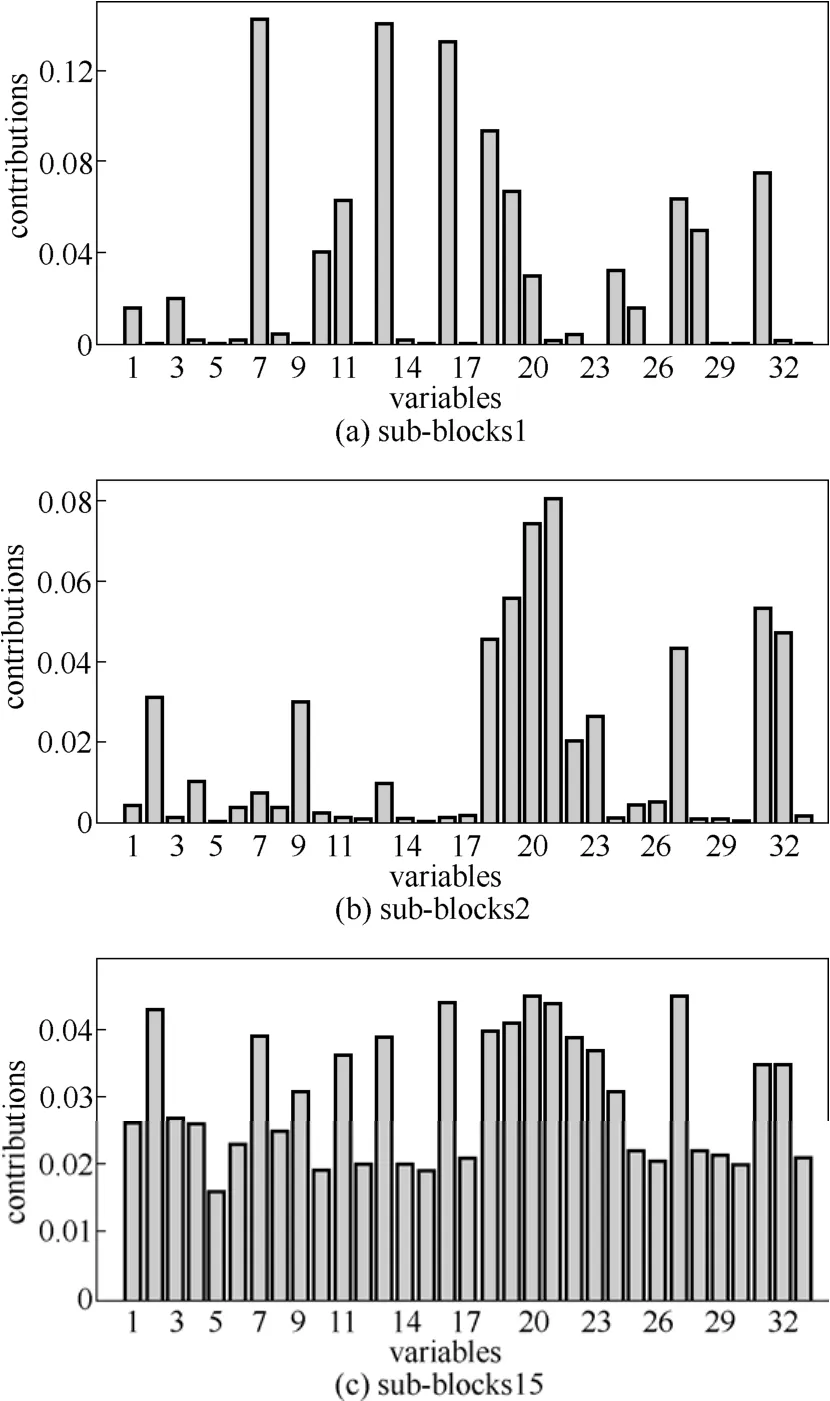
图9　3个子块的变量贡献图Fig.9　Variable contributions in three sub-blocks

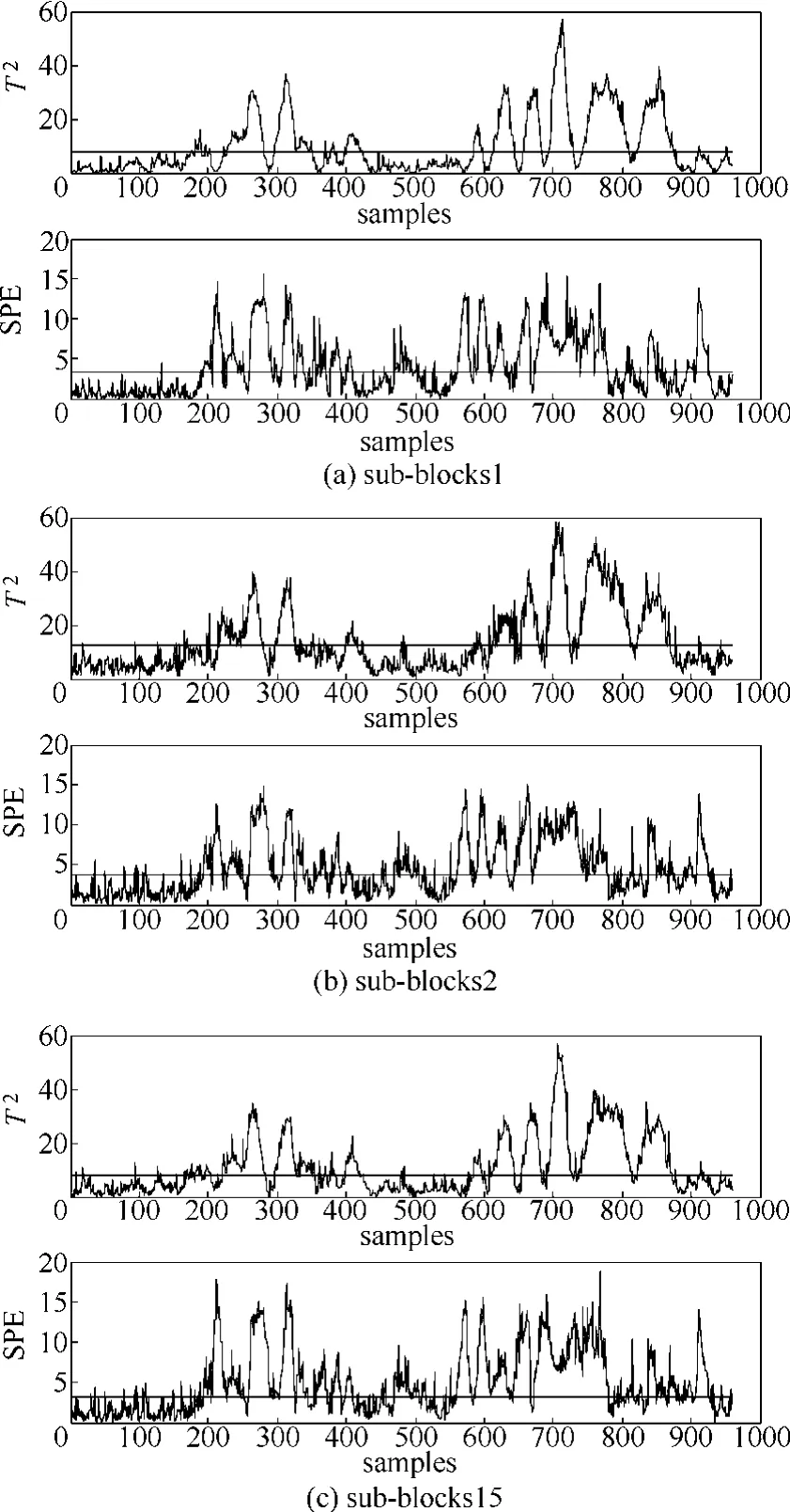
图10　故障10的分布式PCA监测结果Fig.10　Monitoring results of fault 10 by distributed PCA

表4　故障10的监测时间Table 4　Monitoring time of fault 10/s

表4给出了故障10的监测时间，根据表2 中4种监测模型对故障10的漏报率可以得出：分布式ICA-PCA监测模型与ICA-PCA监测模型相比，不仅提高了监测精度，而且提高了监测效率；与分布式PCA模型和PCA模型相比，虽然降低了漏报率，但监测效率也稍低。

考虑每种方法分别对 21种故障监测效率的相似性，结合对表3和表4的分析可知：本文所提方法与PCA方法和分布式PCA方法相比，监测效率稍低；与ICA-PCA模型相比，提高了监测效率。

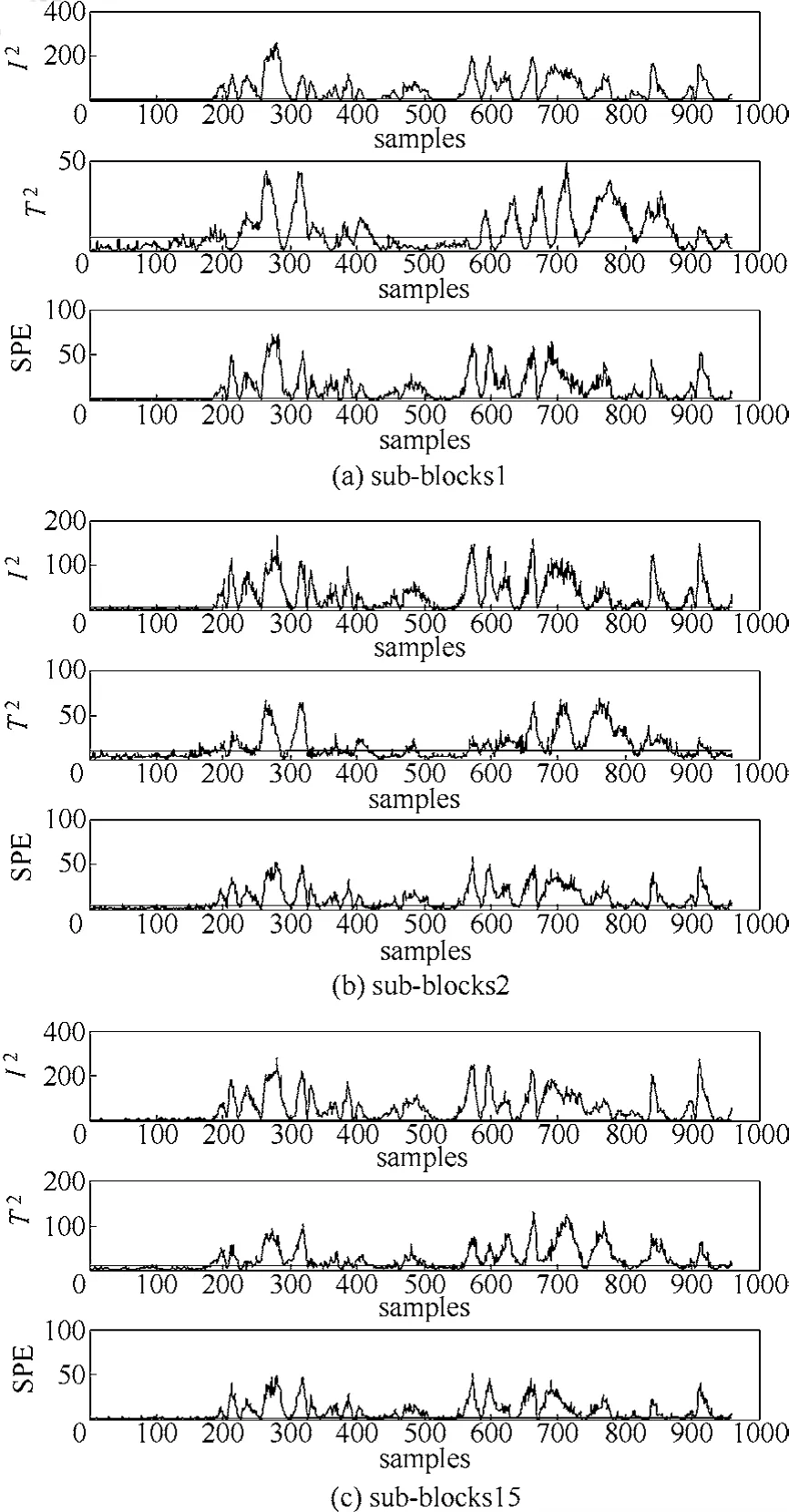
图11　故障10的分布式ICA-PCA监测结果Fig.11　Monitoring results of fault 10 by distributed ICA-PCA

4　结　论

本文提出了一种基于分布式 ICA-PCA模型的工业过程故障监测方法，针对复杂工业过程难以自动划分子块和过程数据的非高斯性，该方法首先通过原始 PCA分解把工业过程自动划分为互不相关的子块，其次对各个子块采用 ICA-PCA的两步信息提取策略，分别提取出子块数据中的高斯信息和非高斯信息，最后构建各子块的 I2、T2和SPE 3个统计量及对应的统计限，并通过变量贡献图确定故障变量，实现故障监测和诊断。TE平台的仿真结果表明所提出方法的性能：该方法适用于复杂工业过程自动划分子块和过程数据存在非高斯信息的情况。

References

[1]Nomikos P, MacGregor J F. Monitoring batch processes using multiway principal component analysis [J]. AIChE J., 1994, 40: 1361-1375.

[2]Nomikos P, MacGregor J F. Multi-way partial least square in monitoring batch processes [J]. Chem. Intell. Lab. Syst., 1995, 30: 97-108.

[3]Ku W, Storer R H, Georgakis C. Disturbance detection and isolation by dynamic principal component analysis [J]. Chem. Intell. Lab. Syst., 1995, 30: 179-196.

[4]Bakshi B R. Multiscale PCA with applications to multivariate statistical process monitoring [J]. AIChE J., 1998, 44: 1596-1610.

[5]Cheng C, Chiu M S. Nonlinear process monitoring using JITL-PCA [J]. Chem. Intell. Lab. Syst., 2005, 76:1-13.

[6]Kim D, Lee I B. Process monitoring based on probabilistic PCA [J]. Chemom. Intell. Lab. Syst., 2003, 67: 109-123.

[7]Zhao Zhonggai (赵忠盖), Liu Fei (刘飞). Factor analysis and its application to process monitoring [J]. Journal of Chemical Industry and Engineering (China) (化工学报), 2007, 58 (4): 970-974.

[8]Zhang Y, Ma C. Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS [J]. Chem. Eng. Sci., 2011, 66: 64-72.

[9]Song Bing (宋冰), Ma Yuxin (马玉鑫), Fang Yongfeng (方永锋), Shi Hongbo (侍洪波). Fault detection for chemical process based on LSNPE method [J]. CIESC Journal (化工学报), 2014, 65 (2): 620-627.

[10]Lee J M, Yoo C K, Lee I B. Statistical process monitoring with independent component analysis [J]. J. Process Control., 2004, 14: 467-485.

[11]Chen Guojin (陈国金), Liang Jun (梁军), Qian Jixin (钱积新). ICA and its application to chemical process monitoring and fault diagnosis [J]. Journal of Chemical Industry and Engineering (China) (化工学报), 2003, 54 (10): 1474-1477.

[12]Lee J M, Yoo C K, Lee I B. Statistical monitoring of dynamic processes based on dynamic independent component analysis [J]. Chem. Eng. Sci., 2004, 59: 2995-3006.

[13]Yoo Chang Kyoo, Lee Dae Sung. Application of multiway ICA for on-line process monitoring of a sequencing batch reactor [J]. Water Research, 2004, 4: 1715-1732.

[14]Ge Z Q, Song Z H. Performance-driven ensemble learning ICA model for improved non-Gaussian process monitoring [J]. Chemometrics and Intelligent Laboratory Systems, 2013, 123: 1-8.

[15]Kano M, Hasebe S, Hashimoto I, Ohno H. Evolution of multivariate statistical process control: application of independent component analysis and external analysis [J]. Comput. Chem. Eng., 2004, 28: 1157-1166.

[16]Ge Z Q, Song Z H. Process monitoring based on independent component analysis-principal component analysis (ICA-PCA) and similarity factors [J]. Ind. Eng. Chem. Res., 2007, 46: 2054-2063.

[17]MacGregor J F, Jaeckle C, Kiparissides C, Kourtoudi M. Process monitoring and diagnosis by multiblock PLS methods [J]. AIChE J., 1994, 40: 826-838.

[18]Westerhuis J A, Kourti T, MacGregor J F. Analysis of multiblock and hierarchical PCA and PLS models [J]. J. Chemom., 1998, 12: 301-321.

[19]Cherry G A, Qin S J. Multiblock principal component analysis based on a combined index for semiconductor fault detection and diagnosis [J]. IEEE Trans. Semiconductor Manufacturing, 2006, 19: 159-172.

[20]Ge Z Q, Song Z H. Two-level multiblock statistical monitoring for plant-wide processes [J]. Korean J. Chem. Eng., 2009, 26, 1467-1475.

[21]Ge Z Q, Song Z H. Nonlinear soft sensor development based on relevance vector machine [J]. Ind. Eng. Chem. Res., 2010, 49: 8685-8693.

[22]Ge Z Q, Song Z H. Distributed PCA model for plant-wide process monitoring [J]. Ind. Eng. Chem. Res., 2013, 52: 1947-1957.

[23]Downs J, Vogel E F. A plant-wide industrial process control problem [J]. Computers &Chemical Engineering, 1993, 17: 245-253.

Fault monitoring of industrial process based on distributed ICA-PCA model

ZHONG Lusheng, HE Dong, GONG Jinhong, ZHANG Yongxian
(College of Electrical Engineering, East China Jiaotong University, Nanchang 330013, Jiangxi, China)

A fault monitoring method based on distributed independent component analysis-principal component analysis (ICA-PCA) model is proposed, which is suitable for complex industrial process that cannot be divided into several sub-blocks through an automatic way and has non-Gaussian information. Firstly, an initial PCA decomposition is carried out upon the variables of the whole process. By constructing sub-blocks through different directions of PCA principal components, the original feature space can be automatically divided into several sub-feature spaces. In addition, a two step extractions of the ICA-PCA information are carried on upon all sub-blocks in order to extract both Gaussian and non-Gaussian information, establishing the new statistics and their statistic limits. Finally, the simulation of TE process shows that the proposed fault detection model is efficient and feasible.

complex industrial process; automatic partitioning sub-blocks; non-Gaussian; ICA-PCA; fault monitoring

引　言

随着工业过程生产规模的不断扩大，对其过程的故障监测已成为过程控制领域的研究热点。其中，主成分分析（PCA）和偏最小二乘法（PLS）在过程监测和故障诊断领域得到了成功的应用。之后研究人员又提出PCA、PLS的拓展方法，并成功应用在故障监测中：Nomikos等[1-2]提出使用多向 PCA 和PLS监测批处理过程；Ku等[3]使用动态PCA实现了故障的监测和分离；Bakshi[4]提出使用基于小波分析的多尺度PCA监测不同频率范围的故障。最近，国内外学者又提出一些新的方法用于工业过程故障监测。Cheng等[5]提出使用实时学习（JITL）和 PCA结合的方法监测非线性静态或动态系统；Kim等[6]指出：针对过程数据存在噪声情况，使用概率主成分分析（PPCA）构建 PPCA故障监测模型；赵忠盖等[7]针对PCA需要噪声各向同性的限制，提出基于因子分析的故障监测模型；Zhang等[8]将核函数的思想引入到多尺度主元分析中，不仅改善了常规PCA在时频域的局部分析能力，而且使其能够处理非线性过程。这些方法通常要求过程数据服从高斯分布[9]，这一条件在复杂的工业过程中却很难满足。

date: 2015-05-04.

ZHONG Lusheng, lszhongzju@163.com

supported by the National Natural Science Foundation of China (61263010, 60904049), the Natural Science Foundation of Jiangxi Province (20114BAB211014) and the Project of Education Department of Jiangxi Province (GJJ14399).

10.11949/j.issn.0438-1157.20150546

TP 277

A

0438—1157（2015）11—4546—09

2015-05-04收到初稿，2015-08-06收到修改稿。

联系人及第一作者：衷路生（1979—），男，博士，副教授。

国家自然科学基金项目（61263010，60904049）；江西省自然科学基金项目（20114BAB211014）；江西省教育厅项目（GJJ14399）。