交互式一体机在小学数学思维活动课设计中的应用

交互式一体机作为一种功能齐全且强大的教学工具，在小学数学教学中展现出卓越的互动教学效果。尤其是在小学阶段，这种工具能够极大地促进师生之间的互动，使课堂氛围更加活跃，体现了以学生为中心的教学理念，有助于激发学生的学习思维，提升他们的数学学习能力。“圆柱与圆锥”是小学数学六年级下册第二单元的内容，属于“图形与几何”的学习范畴，涵盖了圆柱和圆锥的多个方面，包括形状、特性、表面积和体积等。通过这一课的学习，学生能够识别圆柱和圆锥，理解它们各自的特性，掌握计算这两种几何体表面积和体积的公式，并学会将这些知识应用到现实生活中。本文以“圆柱与圆锥”为例，探讨了如何将交互式一体机应用于小学数学思维活动的教学设计中。

一、交互式一体机的“圆柱与圆锥”设计流程

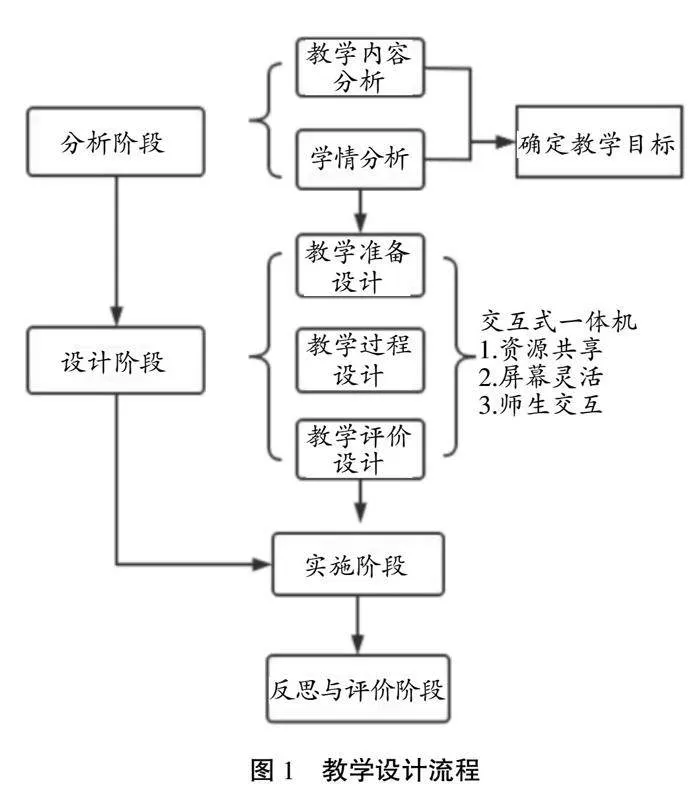
在本课教学中，教师需要按照教学的基本过程分为不同的阶段进行教学设计。图1为基于交互式一体机的“圆柱与圆锥”的教学设计流程，主要包括分析阶段、设计阶段、实施阶段、反思与评价阶段。

二、教学目标、重难点及学情分析

（一）教学目标

1.引导学生对圆柱与圆锥的概念及特征进行深入理解，学会正确运用相关公式来计算它们的表面积和侧面积。同时，培养学生仔细分析问题的能力，并能够针对相关问题运用灵活的解题思路和方法。

2.灵活掌握立体几何的学习、计算和应用方法，提高学生的创新和创造能力。

3.认识数学和立体几何知识在生活中的作用和价值，让学生对数学产生浓厚的学习兴趣。

（二）教学重难点

1.教学重点

理解和掌握圆柱、圆锥的基本特征及其结构。

（1）认识圆柱的底面、侧面和高，认识其展开图。

（2）认识圆锥的底面、侧面和高，理解圆锥的顶点和母线。

2.教学难点

理解体积公式的推导过程。

（1）理解用底面积乘以高为什么能够计算出圆柱体积。

（2）理解圆柱和圆锥的底和高相同，但圆锥体积却是圆柱体积三分之一的原理。

（三）学情分析

1.数学思维能力

六年级学生正处于数学思维能力迅速发展的阶段，已经掌握了基本的数学概念和运算技能，能够进行初步的逻辑推理和问题解决。在“圆柱与圆锥”的教学活动中，教师可以利用学生的这一能力，设计富有挑战性的问题和活动，引导学生深入探索数学概念。例如，通过比较不同圆柱和圆锥的体积和表面积，学生不仅能够加深对几何形状属性的理解，还能够锻炼比较、分类和推理能力。

2.学习风格差异

学生之间的学习风格差异显著。视觉型学生偏好图表和图像，听觉型学生更倾向于通过听讲来吸收信息，而动手操作型学生则通过实践和制作来加深理解。在设计“圆柱与圆锥”的数学思维活动时，教师需综合运用多媒体教学工具，如动画演示、模型操作、互动讨论等，以适应不同学习风格的学生。

三、基于交互式一体机的小学数学思维活动设计——以“圆柱与圆锥”为例

（一）基础知识梳理

在小学数学“圆柱与圆锥”教学中，教师通过交互式一体机来梳理基础知识，能有效地提高教学质量，增强学生对数学概念的理解。教师可以借助交互式一体机把圆柱和圆锥的基本特征展示出来。直观的三维展示与清楚的文字标记在屏幕上帮助学生更好地辨识圆柱及圆锥的各种构造。教师在讲解“圆柱和圆锥”相关知识的过程中，应详细阐述其底部、侧面和高的含义以及彼此之间的联系。学生有机会通过触摸显示屏对模型进行操作分类，并从各种不同的视角来查看其形态。

（二）复习旧知

师：同学们，我们之前也学过一些立体图形，大家回想一下，都有哪些立体图形？

生：老师，我记得我们之前学过正方体和长方体。

师：很好！你还记得我们是从哪些方面学习这些立体图形的吗？

生：学习了正方体和长方体的面、边和顶点，还有这些立体图形的展开图。

师：回答正确。还有其他立体图形吗？

生：老师，我们之前还学习了球体。

师：对，球体也是我们学习过的。那你记得我们是怎么描述球体的吗？

生：球体没有面和边，只有一个曲面。

师：说得非常好！还有其他回答吗？

生：老师，棱柱和棱锥也是我们之前学过的。

师：没错！还记得它们的特点是什么吗？

生：棱柱的两个底面是平行的，而且底面相等，侧面是矩形或三角形；棱锥有一个底面，侧面是三角形连接到一个顶点。

师：非常棒！大家对之前学过的知识还都有记忆。今天我们来学习新的立体图形：圆柱和圆锥。

（三）探究新知

1.教师可以把交互式一体机课件中的圆柱与圆锥物品展示给学生。

师：大家仔细观察一下大屏幕中的图形，这些圆柱与圆锥物品在日常生活中很容易见到，相信大家一定不陌生。这些物品由不同的颜色和材料构成，使图形的外部特征更加明显。现在，老师要把图形的外部特征消除掉，观察并分析这两种图形在几何结构上有哪些地方相似。

教师通过触摸屏幕把图形上的颜色和材料去掉。

师：我已经把这些图形的外部特征去掉了，图形看起来更加抽象了，呈现出圆柱和圆锥两类图形，圆柱形物体和圆锥形物体分别就是圆柱形和圆锥形。大家通过观察思考一下老师刚才提出的问题。

生：老师，我通过观察发现，圆柱和圆锥的底面都是圆形的，而且都有一个侧面。

师：很好！那么它们有什么不同点吗？

生：圆柱有两个圆形底面，圆锥只有一个圆形底面。

师：非常正确！同学们再仔细观察一下，圆柱和圆锥的侧面有共同点吗？

生：这两种图形的侧面都是曲面。

师：非常好！看来大家都认真观察了。接下来，老师利用一体机向你们展示更多的图形，大家按照圆柱形和圆锥形进行归类。

教师可以让学生亲自触摸一体机屏幕把两种图形区分开来，调动学生的学习热情。

此外，教师可以设计一些具体的任务，让学生计算不同半径和高度的圆柱和圆锥的表面积。通过交互式一体机，学生能够拖动滑块或输入数值来改变几何体的参数，并实时看到体积的变化。这种直观的操作不仅能够帮助学生理解公式的实际应用，还能够使学生感受到不同参数对面积的影响，以动态形式掌握数学概念。教师可以利用互动式一体机列出计算圆柱和圆锥表面的题目。

★与圆柱形相关的题目：（1）一个圆柱的底面半径是5厘米，高是10厘米，求这个圆柱的表面积。（2）一个圆柱的底面直径是12厘米，高是底面直径的一半，求这个圆柱的表面积。（3）一个圆柱的表面积是250平方厘米，底面半径是5厘米，求这个圆柱的高。

★与圆锥形相关的题目：（1）一个圆锥的底面半径是4厘米，高是6厘米，求这个圆锥的表面积。（2）一个圆锥的底面直径是10厘米，母线长13厘米，求这个圆锥的表面积。（3）一个圆锥的侧面积是150平方厘米，底面半径是5厘米。求这个圆锥的母线长。

2.总结圆柱与圆锥的基本特征

师：同学们看一下老师手里的这个模型，这是一个圆柱形的物体，大家仔细观察，分析圆柱形的组成结构。

生：老师，圆柱有一个上面、一个下面，并由一个侧面进行连接。

师：回答正确。这位同学刚刚回答的上面和下面实际上就是圆柱的底面。所以说，圆柱的组成结构就是两个底面和一个侧面。

教师在一体机屏幕上进行轻触操作，切换到下一页的教学内容。

师：除了圆柱形模型，老师今天还准备了圆锥形模型，大家继续观察，分析圆锥图形的组成结构。哪位同学能回答一下？

生：圆锥有一个尖尖的顶部。

师：很好！这个尖尖的顶部就是圆锥的顶点。

生：老师，圆锥下面还有一个圆形的部分。

师：这位同学观察得非常仔细，圆形部分就是圆锥的底面。除了顶点和底面，再仔细观察，还有什么发现吗？

生：圆柱底面的连接点是侧面，那圆锥的顶点和底面的连接点也是侧面吗？

师：对！连接顶点和底面的曲面部分就是圆锥的侧面。圆锥由三个部分组成，分别是顶点、底面和侧面。

3.认识圆柱与圆锥的侧面展开图

师：通过刚才的学习，关于圆柱和圆锥的基本构成，大家都明白了吗？

生：明白了！

师：好！圆柱形和圆锥形的区别在于前者有两个底面，后者只有一个底面。那么新问题又来了，如果将这两个图形的侧面分别展开会得到什么结果呢？

教师拿出提前准备好的塑料杯、斗笠等物品，并组织学生进行小组合作学习，引导学生讨论。

生：老师，我觉得塑料杯的侧面展开后有可能是一个矩形。

师：你是怎么分析的呢？

生：因为塑料杯是圆柱形，它的侧面是直的，上下的宽度相同，展开后应该是一个矩形。

师：很有道理，斗笠属于圆锥形，将其侧面展开后会出现什么形状呢？

学生进行激烈的讨论。

生：老师，我们小组一致认为斗笠的侧面展开后应该是一个扇形。

师：为什么会这样认为呢？

生：因为斗笠的侧面是弧形的，侧面展开位置从顶点开始，所以，展开后很有可能是一个扇形。

师：大家通过合作学习与探讨，了解了圆柱和圆锥侧面展开后的形状，也是需要大家记住的知识点。

教师可以将塑料瓶和斗笠的一面剪开，通过演示验证讨论的结果，让学生得到一个确切的答案。这样不仅激发了学生的学习兴趣，还极大地提高学生的观察力和团队合作能力。同时，教师可以轻触一体机屏幕，将提前制作好的动态课件展示出来，带给学生更加直观的学习体验，有利于学生加深对知识的理解。

4.学会计算圆柱与圆锥的表面积

通过以上学习环节，学生对圆柱和圆锥的形状、组成部分以及侧面展开形状有了一定的了解。在此基础上，教师在大屏幕中展示圆柱和圆锥表面积计算公式：

圆柱的表面积公式：S=2πr（r+h）

圆锥的表面积公式：S=πr2+πrl

师：接下来，我们要学习如何计算圆柱与圆锥的表面积，大屏幕中为两种图形的表面积计算公式。π是圆周率，r代表底面圆的半径，h代表圆柱的高。圆锥的表面积公式中，π是圆周率，r是底面圆的半径，l是圆锥的母线长。哪位同学能回答一下，圆柱的表面积需要怎么计算出来呢？

生：老师，圆柱的表面积是不是底面积加侧面积再加一个底面积？因为圆柱有两个底面。

师：很好，圆柱的表面积=侧面积+两个底面积，得出公式S=2πr（r+h）。那么，如何计算圆锥的表面积呢？

生：老师，我知道圆锥的底面积就是圆的面积，所以是侧面积+底面圆面积的和。

师：这位同学总结得非常正确，圆锥的表面积就是S=πr2+πrl，希望大家记住圆柱和圆锥表面积计算公式，并将学到的知识运用到实际中。

（四）教学评价

1.项目式评价

组织学生分组，完成一个复杂立体图形的体积计算项目，如设计一个由多个圆柱和圆锥组成的建筑模型，并计算其总体积。学生可以利用交互式一体机进行协同操作和讨论，最后展示学习成果。教师根据学生的合作情况、解决问题的策略以及最终结果进行综合评价。

2.思维发展评估

（1）思维导图

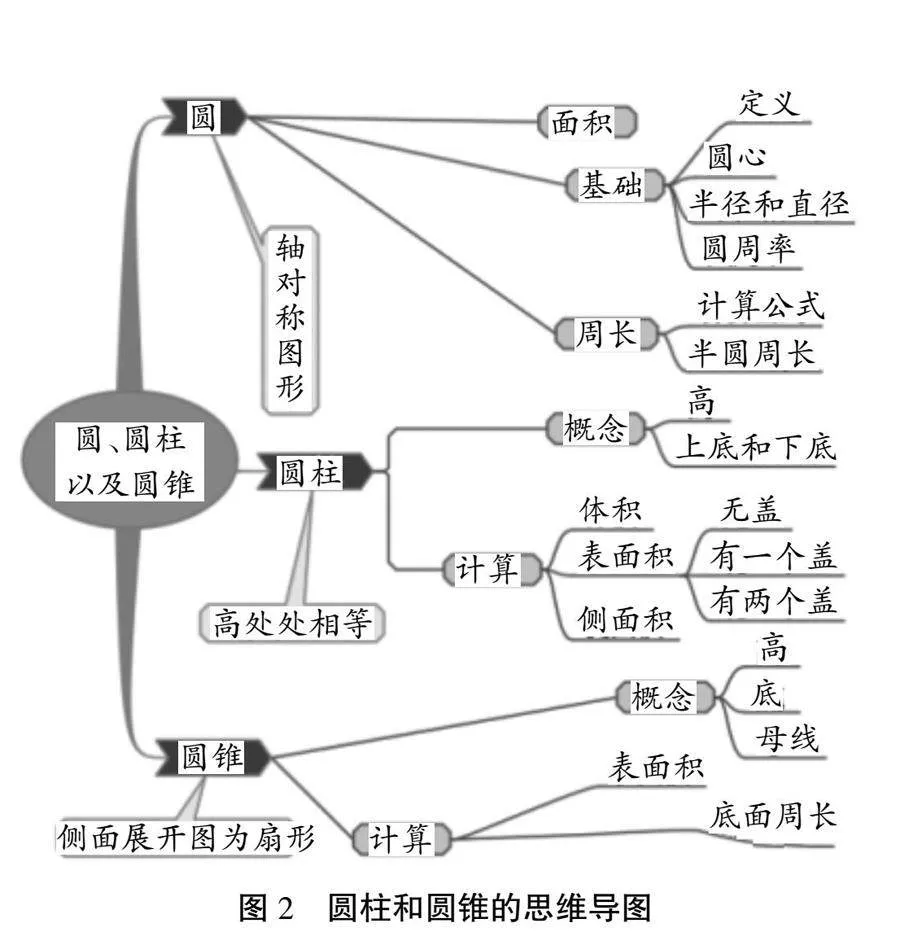
教师要求学生利用交互式一体机绘制思维导图（见图2），展示学生对圆柱和圆锥体积概念的理解过程。这可以包括公式的推导、实际应用例子以及解决问题的步骤等。通过思维导图，教师可以评估学生的逻辑思维能力和知识结构。

（2）自我反思与互评

学生可以在学习结束后，通过填写电子问卷或录制视频，反思自己在学习过程中的收获与不足。同时，学生之间可以相互评价作业或项目，分享学习心得，促进彼此进步。

四、教学思考

在使用交互式一体机之前，教师需要明确教学目标，从而设计出针对性和有效性的活动。对于“圆柱与圆锥”的教学，交互式一体机可以提供多种功能，如模拟计算、互动练习等。在设计活动时，教师需要合理运用这些功能，使学生能够充分利用一体机的优势，增加学习的互动性和趣味性。教师应掌握交互式一体机的使用方法和功能，成为学生学习的指导者和引导者，鼓励学生积极探索和思考，改善教学质量，提高学生的学习能力和解决问题的能力。

（作者单位：贵州省大方县黄泥塘镇鸡场小学）

编辑：温雪莲