一类弱监督数据中多视角扰动的特征选择方法

摘 要： 弱标签消歧技术可以用来消除数据中的噪声标签.然而，经由弱标签消歧后的数据中依然可能存在冗余或不相关特征，因此带来了弱监督数据中的特征选择这一实际问题.在弱标签消歧后得到的数据的基础上，提出了一种基于多视角扰动的特征选择框架，其能够分别从样本和特征多个视角出发，构造不同的扰动数据，以便求解出多个不同的特征选择结果，从而为后续的学习任务提供基础性集成工具.此外，所提的多视角扰动特征选择框架适用于不同类型、不同约束下的搜索进程.在12组高维数据上，通过注入5种不同比例的标签噪声和使用3种不同类型的特征度量准则，实验结果表明，所提方法求得的特征选择结果能够从准确率和稳定性的层面极大地提升分类性能.

关键词： 特征选择；多视角；粗糙集；超集学习；弱监督

中图分类号：TP181"" 文献标志码：A"""" 文章编号：1673-4807（2024）02-101-08

Feature selection via multi-view perturbation in a typeof weakly supervised data

Abstract：Technique of disambiguation of weak labels can be used to remove noisy labels for samples from data. However，redundant or irrelevant features may also be observed after disambiguation of weak labels， so the problem of feature selection should be paid much attention to in weakly supervised data. On the basis of the data with disambiguation of weak labels， a general feature selection framework via multi-view perturbation is developed， which can construct different perturbed data from both the levels of sample and feature. Consequently， multiple results of feature selection can be obtained， which provide a basic integration tool for the subsequent learning. The proposed framework can be applied to various forms and constraints of searching. On more than 12 sets of" high-dimensional data， by injecting 5 ratios of label noise and using 3 criteria of feature evaluation， the experimental results demonstrate that the feature selection results obtained by our proposed method can significantly improve the classification performance from both the aspects of classification accuracy and classification stability.

Key words：feature selection， multiple-view， rough set， superset learning， weak supervision

在机器学习框架中，有监督学习[1-3]在建模时采用强监督假设，即对象的类别信息是单一、明确的.而众多的实际工程应用需求表明，数据的标注成本很高、获取大量类别标注精确的样本难度巨大，因此近年来弱监督学习[4-7]已然受到了重点关注.与有监督不同是，弱监督学习一般是采用有限、含有噪声或者类别标注不准确的数据来进行模型的训练，因此，研究弱监督场景下数据的有效利用和模型性能的提升具有现实的应用价值.

超集学习是一种典型的弱监督学习框架[6-9]，出现在诸多现实场景中，如人脸识别、生物信息学、自然语言处理等，近年来得到了广泛的重视.在该框架中，每个样本的标签不再具有单一性和明确性，而是对应着一个“候选标签集合”，样本的唯一真实标注隐藏在该候选标签集合中.在利用此类具有歧义性的样本进行学习建模时，一个直观的策略是对候选标签集合进行“消歧”，这一过程可被称为弱标签消歧.弱标签消歧可以有效地消除数据中的噪声标签，从而提升后续模型的学习性能.目前比较典型的超集学习算法有PL-kNN[8]，PL-SVM[9]等，其中，PL-kNN和PL-SVM都是基于弱标签消歧的超集学习算法.此外，某些标签重构方法也可以被应用在弱标签消歧问题中，例如P-LLE[10]算法已经被证实其重构的标签能够为学习器带来较好的泛化能力.

特征选择，作为一种数据预处理技术，可以在建立分类模型之前识别和删除不相关或冗余的特征，从而提高数据在维度上的质量，降低后续学习器在数据集上的训练代价.需指出的是，在弱监督学习问题中，虽然弱标签消歧是一种提升学习模型性能的有效方法，但是经弱标签消歧后的数据中依然可能存在冗余或不相关特征.因此近年来已有学者对于弱监督数据中的特征选择问题进行了探究，文献[11]基于弱标签消歧的结果，利用信息熵研究了消歧后数据中的特征选择问题.但由于弱标签消歧本身并不能保证所有样本的真实标签都能够被完美重构，因此所选择出的特征的性能依然值得商榷.

近年来，在特征选择相关任务中，引入集成的基本理念，已被证实可以显著提升所选特征在测试样本上的表现力.此外，基于集成的特征选择方法还具有显而易见的灵活性，主要体现在集成策略的多样性上.鉴于此，在弱监督数据中研究基于集成的特征选择方法，有望为复杂数据中的特征选择问题带来框架性的有效方案.为了达到这一目的，笔者将在本研究中给出一种基于多视角扰动的集成特征选择框架，在这一框架中，在弱标签消歧的基础上，分别从样本和特征的视角实现数据扰动，从而构造出多个具有显著差异性的扰动数据；进一步地，针对每一个数据进行特征选择；最后利用所得到的多个特征选择结果在测试样本上进行投票分类.

1 相关工作

1. 1 邻域粗糙集

1. 2 弱标签消歧

超集学习是一种典型的弱监督学习模式.在超集学习框架中，对于某个xi ∈ U， xi的候选标签可能不止一个，而是一组，即d（xi）∈P（Vd）而非d（xi）∈Vd， 此处P（Vd）表示集合Vd的幂集.因此在超集学习框架中，若xi∈U， 有|d（xi）|=1（|X|表示集合X的基数）， 则称DS为一个实例决策系统，否则称DS为一个超集决策系统.需注意的是，在超集决策系统中，虽然xi∈U使得|d（xi）|gt;1， 但弱标签合集d（xi）中仅仅只有一个标签是与样本xi关联的真实标签.

给定一个超集决策系统DS， 显然可以通过组合的方法构造出多个不同的实例决策系统形如DS′=U，AT，d′. 其中Symbolb@@xi∈U， 有d ′（xi）∈d（xi）. 因此，若超集决策系统DS中有t个不同的标签，m个样本，则在最坏情况下，可以构造出t m个不同的实例决策系统.

然而，在弱监督环境中，如何从样本的候选标签集中甄别出可能的真实标签，或者说弱标签消歧是一个核心问题.换言之，从标签的视角来看，弱标签消歧的目的是在训练数据中，找寻“合理”的实例决策系统，即将一个超集决策系统转换成为一个“合理”的实例决策系统.如提出了P-LLE算法[12]，该算法可以在多项式时间内重构实例决策系统.借鉴其基本思想，从邻域的基本结构出发，基于邻域的P-LLE算法的基本流程：

1. 3 基于约简的特征选择

约简是粒计算研究领域中一类有效的特征选择方法，其能够在给定的约束条件下，找到满足该约束的最小特征子集.虽然算法1可以在超集决策系统中通过采用弱标签消歧的方式来提升后续学习器的性能，但从特征维度的视角来看，决策系统中依然可能存在冗余或不相关特征.鉴于此，文献[13]在弱标签消歧的基础上，研究了相应的特征约简问题，其一般定义如下所示.

（1） A满足DS′里对应的约束条件；

（2）A， B不满足DS′里对应的约束条件.

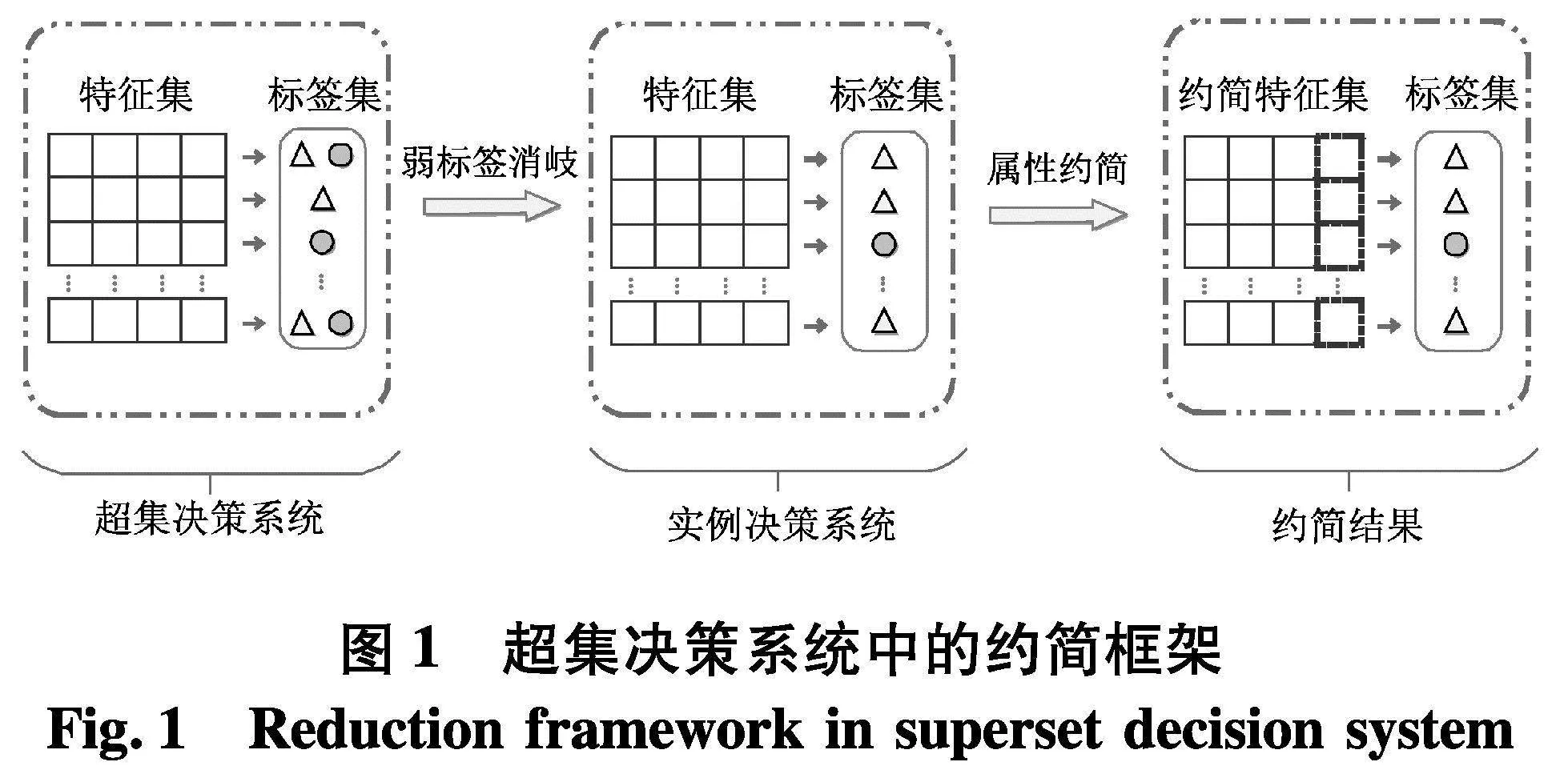
综上，给定一个超集决策系统，经由弱标签消歧后求解约简的一般框架结构如图1.

2 研究方法

2. 1 几种度量

在超集决策系统中，经由弱标签消歧，得到了一个实例决策系统[11].进一步地，在该实例决策系统中引入条件熵，并利用这一度量设计了约简的约束条件.然而，在粒计算及粗糙集相关领域的研究中，度量的形式是非常丰富的，利用邻域粗糙集，不仅可以求得实例决策系统中的条件熵，还可以求得诸如近似质量、鉴别指数等度量指标以刻画实例决策系统中的不确定性.

式中：δA（xi）为样本xi在实例决策系统DS′中的邻域；U / IND（d′ ） ={X1， X2， …， Xt}， d ′表示在实例决策系统DS′中所有与样本xi具有相同消歧后的标签所构成的集合.

2. 2 约简的前向贪心求解

在文献[13]中，期望求得一个约简A，使得A能够在实例决策系统中带来最小的条件熵.又因为本研究中采用的是邻域方法对样本空间进行信息粒化，因此条件熵在实例决策系统DS′中具有单调变化的趋势，即随着特征数量的减少，条件熵会保持不变或者逐渐增大.从这一视角来看，利用条件熵这一度量指标，进行约简求解就是期望能够找到一个最小的特征子集，其能够保持条件熵不会增高.目前，已有大量的算法能够用于求解给定约束条件的约简，但兼顾时间效率和约简的有效性，前向贪心搜索是一种非常流行的方法，其一般流程为：

6.输出A.

2.3 约简的多视角扰动求解

虽然算法2可以快速地在实例决策系统中求解出一个约简，但约简的性能往往是研究者们更加关注的问题.近年来，为了进一步提升约简的有效性，已有众多学者在约简求解问题中引入了集成策略，大致可以分为两类：① 在约简求解过程中引入集成机制，帮助搜索过程更好地对候选特征进行评估，进而挑选出更为稳健特征以利于后续的学习[15]；② 重复利用某一搜索或者利用不同的搜索进程，找出多个不同的约简，为后续的学习提供基础性集成工具和单元[16].

一般来说，在上述两种方法中，后者相较于前者来说，框架的搭建和使用更为灵活，且后者能够较大幅度地提升下游学习任务的性能.鉴于这一考虑，文中将从数据的多视角扰动层面出发，利用算法2在不同的数据中求解多个约简，最终实现对测试样本的集成分类.

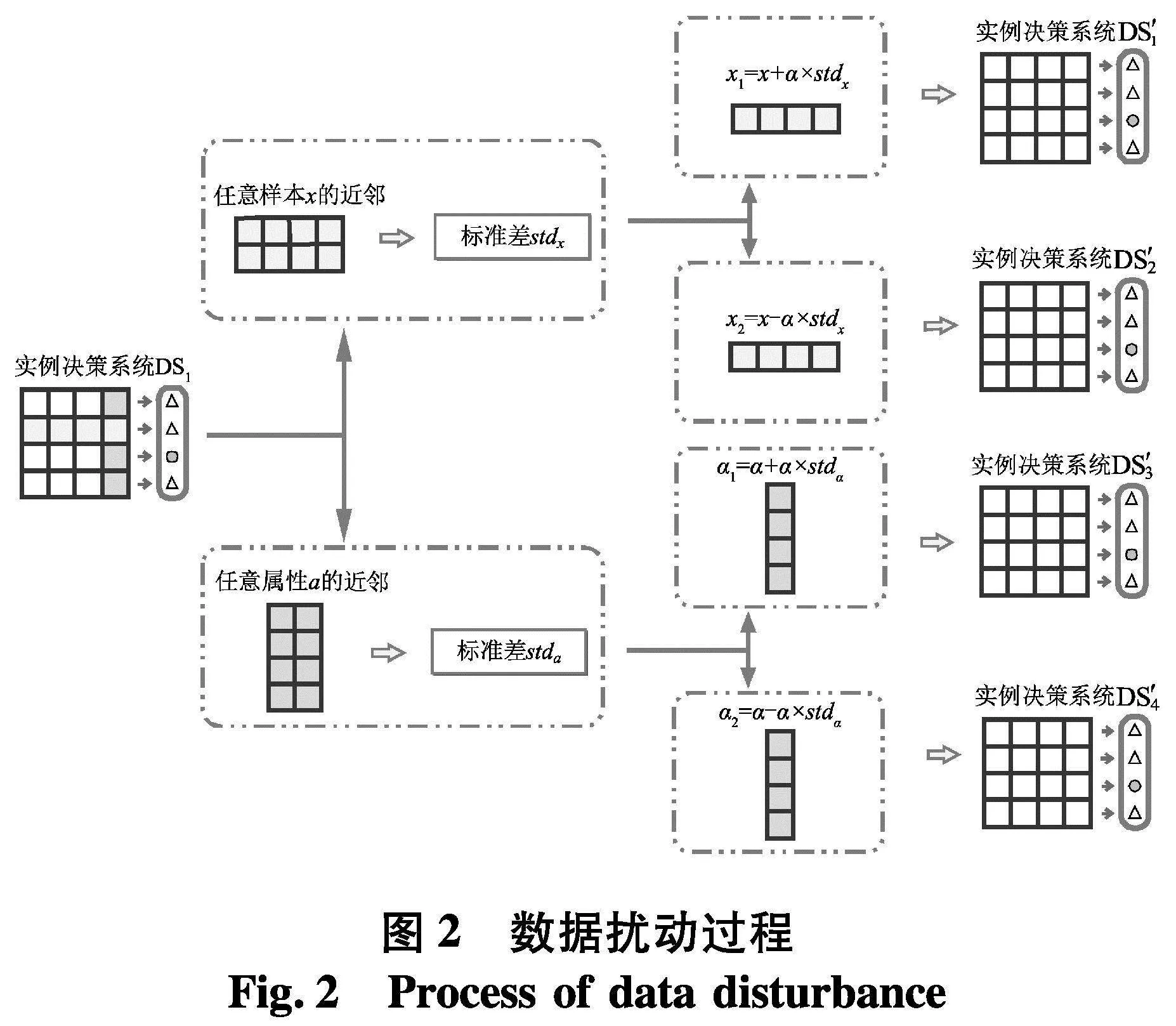
首先，分别从样本和特征两个视角出发，找出U中每个样本x的近邻和AT中每个特征a的近邻；其次，利用近邻求得的标准差将实例决策系统扩充为4个扰动后的实例决策系统；其次，分别在原始实例决策系统和扰动后的实例决策系统中进行约简求解；最终，利用得到的5个约简结果对测试样本进行集成分类.数据扰动过程的基本框架结构如图2.

3 实验分析

为了验证所提算法的有效性，本节进行了相关的实验及对比分析.所有实验均采用Matlab R2017b实现，操作系统为Windows 10， CPU为Intel Core（TM） i5-4210U， 内存为8.00 GB.

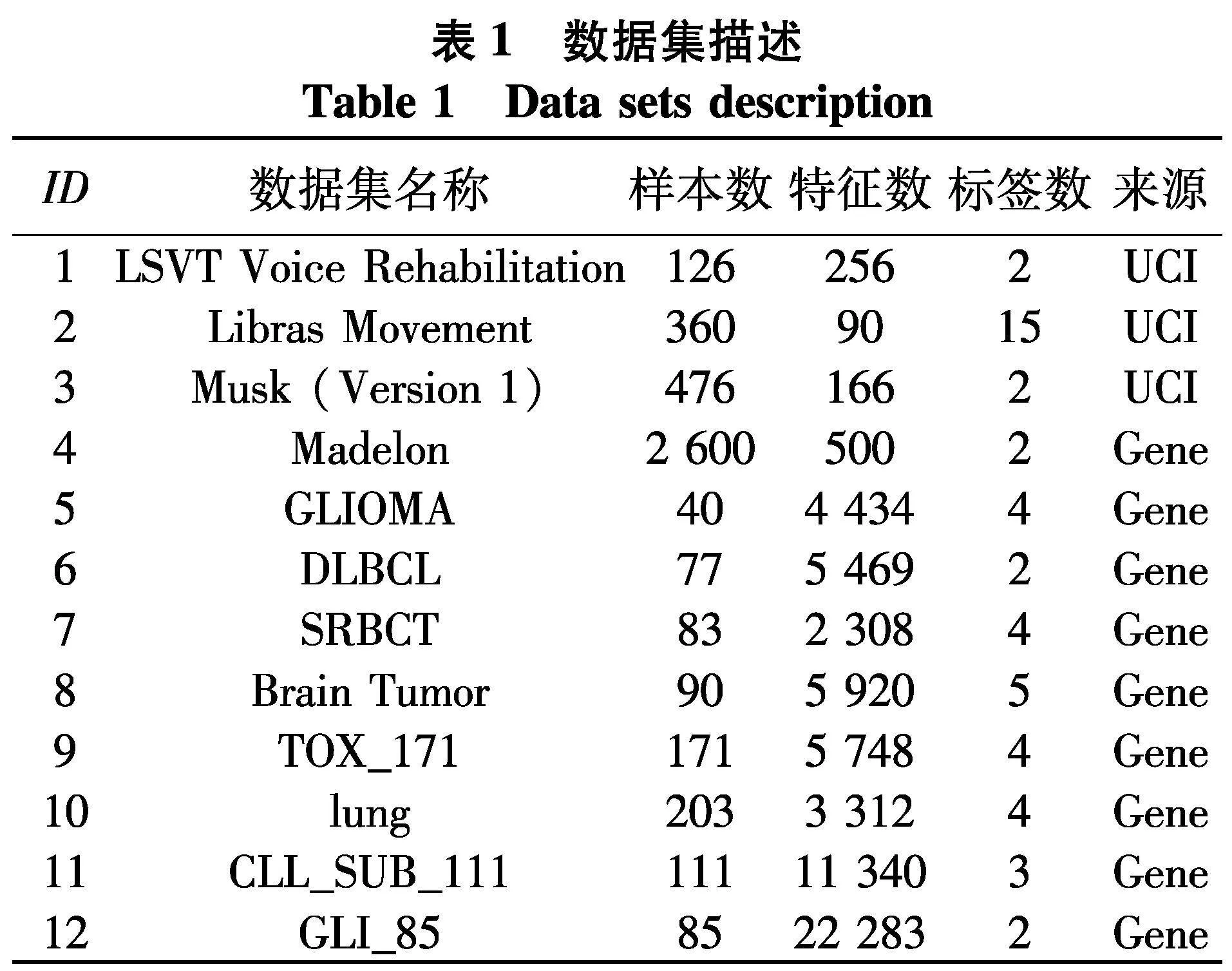
实验从UCI和基因库数据集中共选取了12组数据，大多数数据都是高维数据，基本信息如表1.[KH*2D]

依据图2的数据扰动过程，实验取α=3，近邻个数为15.实验采取了10折交叉验证[17]的方法测试算法的性能，即将数据按照样本数量分为10等份，每次取其中的9份进行约简求解，1份作为测试集，以测试所求得约简的分类性能.

在实验中，使用了PL-kNN[8]分类器对测试数据集进行分类，该分类器中的参数设置为k=3. 对于每一个数据集，[JP3]通过设置百分比β为样本注入弱标签，β的取值分别为5%， 15%， 25%， 35%和45%. 例如，当β为15%时，随机选取15%的样本，为这些样本随机地分配除自身真实标签以外的一些标签.

3.1 第一组实验

因为文中研究是建立在邻域粗糙集基础上的，因此选取了0.04， 0.08， …， 0.40等10个不同的半径以构建不同尺度的邻域关系.第一组实验共进行了6种约简方法后的分类性能的比对，分别是前向贪心-γ、数据扰动-γ、前向贪心-CE、数据扰动-CE、前向贪心-NDI、数据扰动-NDI. 例如，前向贪心-γ表示利用前向贪心搜索在求解以近似质量γ为度量的约简后所对应的性能，数据扰动-γ表示利用图2所示的数据扰动方法在求解以近似质量γ为度量的约简后所对应的性能.

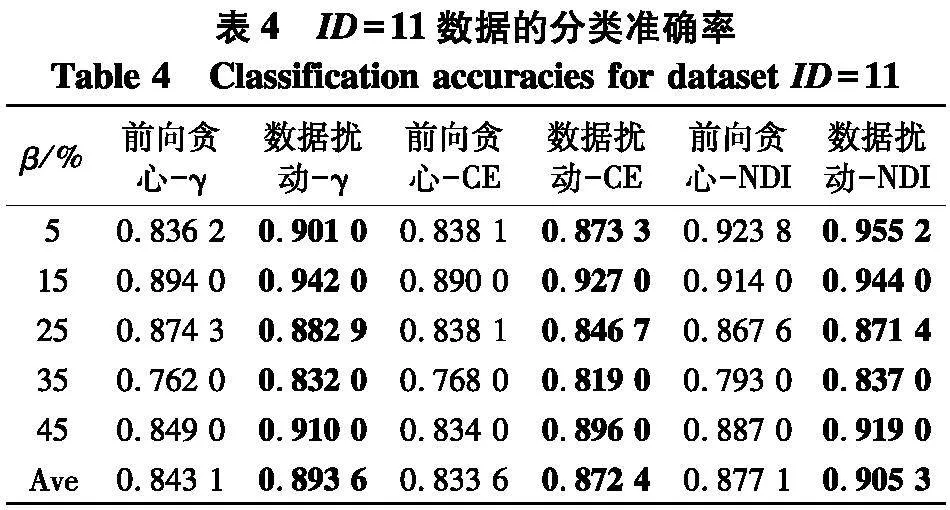
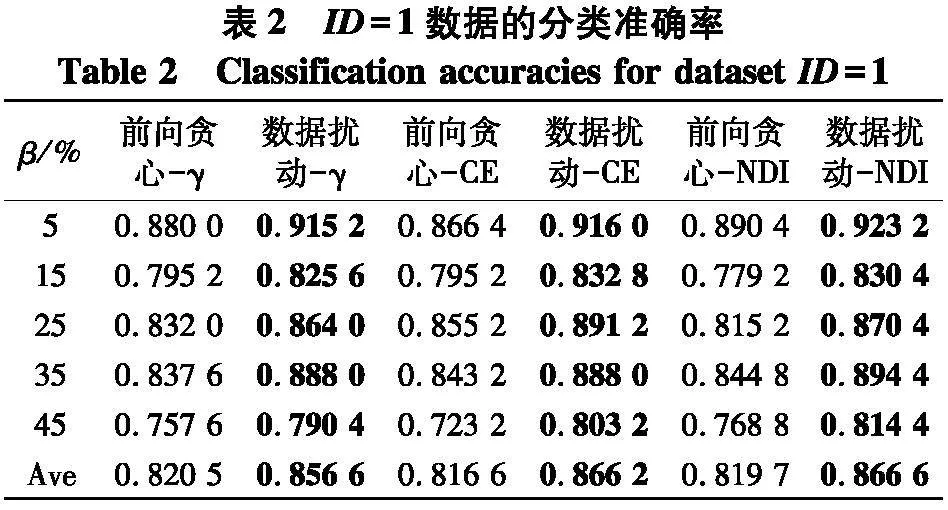
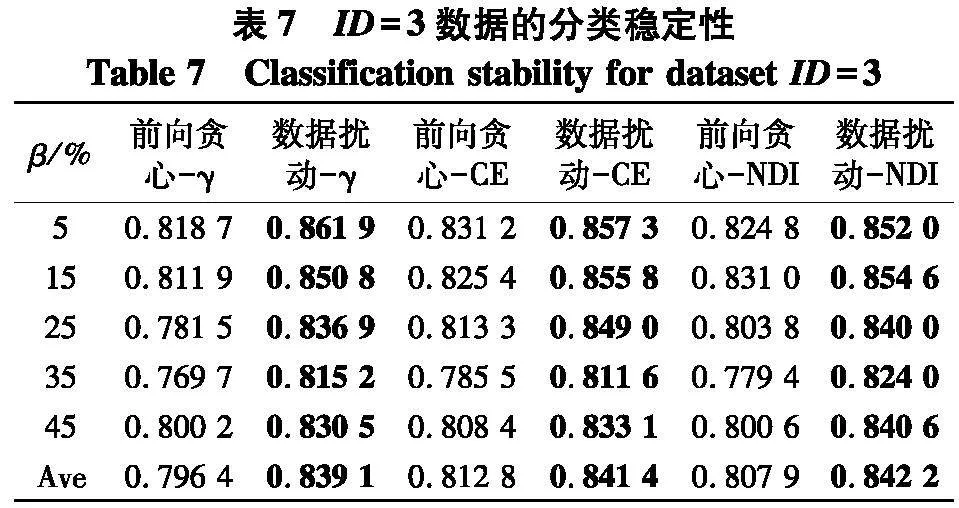
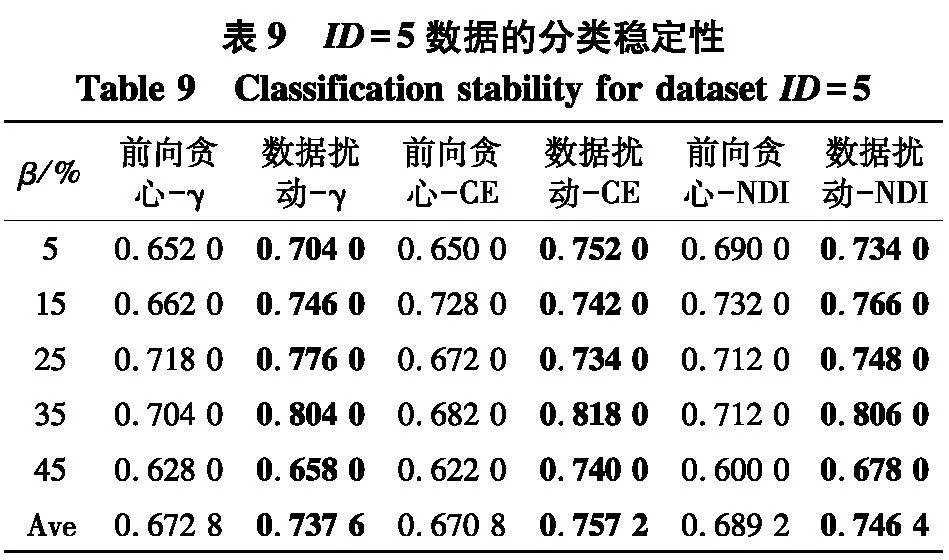
实验使用2个指标来对比不同方法的性能：① PL-kNN分类器所得到的平均分类准确率；② PL-kNN分类器所得到的平均分类稳定性.具体实验结果如表2～9.

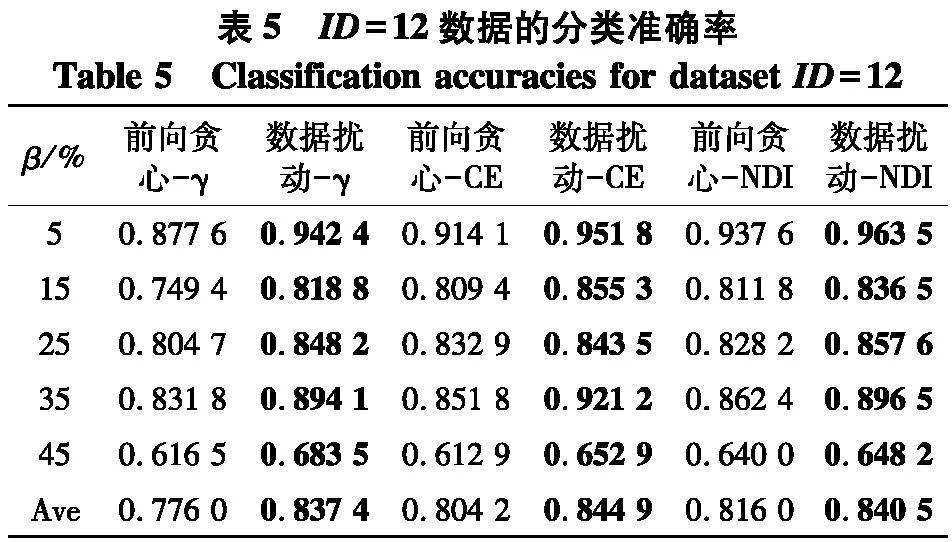
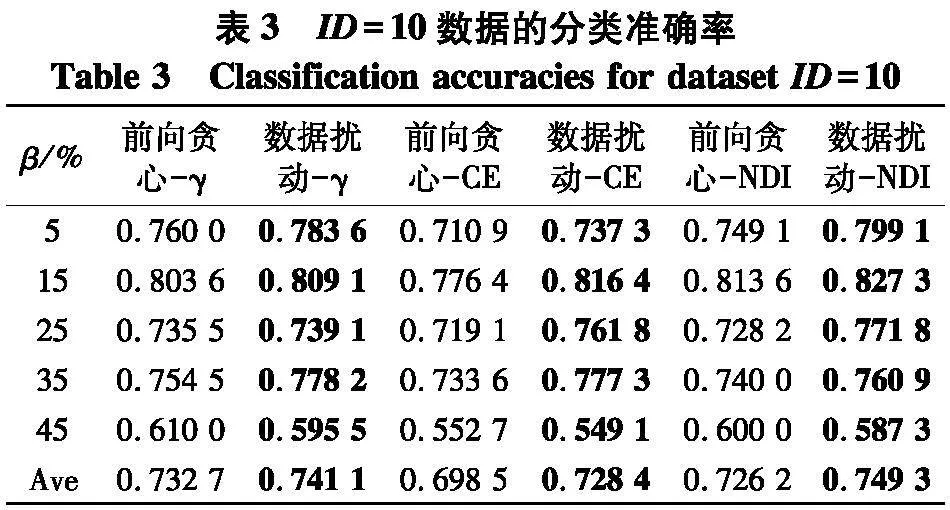
根据表2～5的结果，不难得出以下结论：

（1）随着百分比β的增大，在6种约简方法所对应分类准确率上，性能都有下降趋势，但这并不是严格单调的，这说明在数据中随着弱标签样本比例的不断增大，无论采用哪种约简策略，约简后分类器的性能也会有所下降；

（2）无论使用哪种度量，采用数据扰动生成多个约简的策略，相较于前向贪心搜索来说，都能够取得更高的分类准确率，这说明利用数据扰动的方法，能够产生具有显著差异的约简，进而能够帮助提升投票分类的性能.

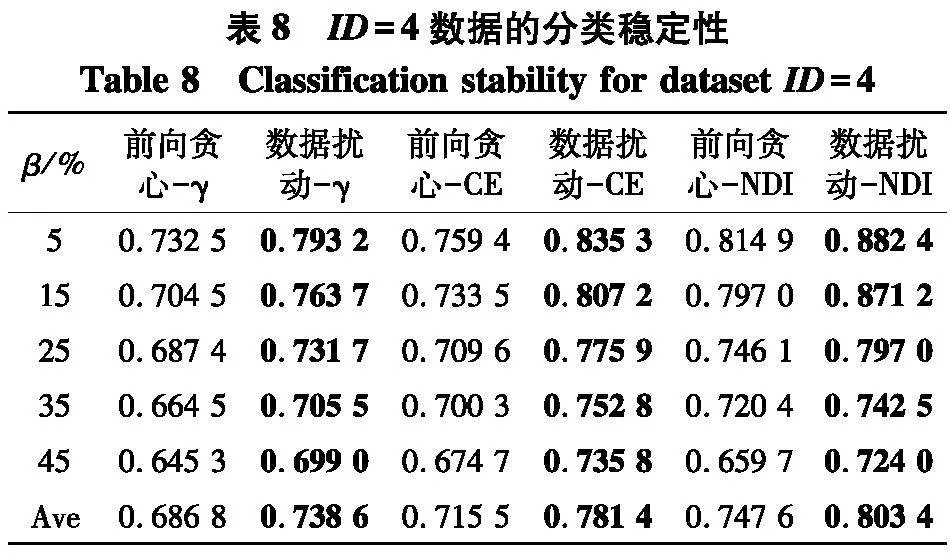
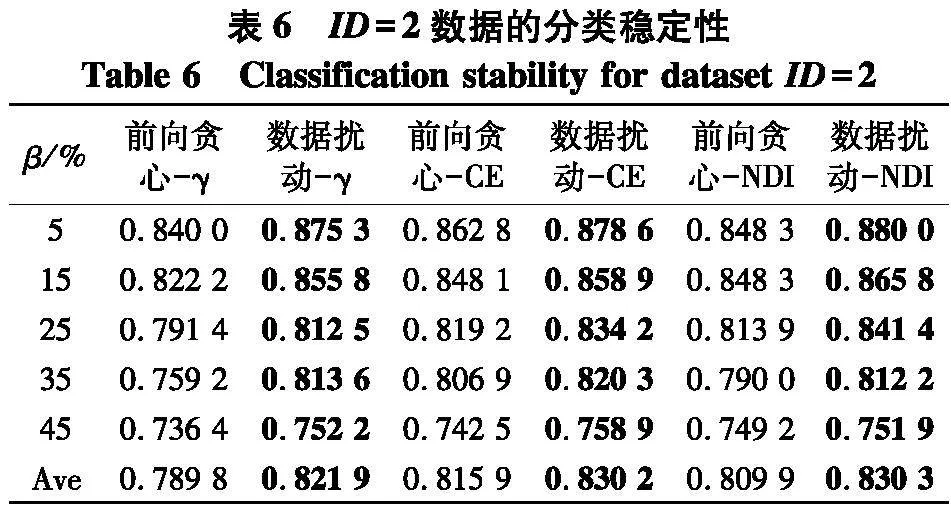
根据表6～9的结果，不难得出以下结论：

（1） 随着百分比β的增大，在6种约简方法所对应分类稳定性上，性能都有下降趋势，但与分类准确率的情形类似，稳定性的下降并不是严格单调的，这说明弱标签样本在数据中的比例对于约简求解后对应的分类稳定性也存在着影响；

（2） 与分类准确率情形类似，无论使用哪种度量，采用数据扰动生成多个约简的策略，相较于前向贪心搜索来说，都能够取得更高的分类稳定性.

3.2 第二组实验

本组实验选取了0.08， 0.16， …， 0.40等5个不同的半径以构建不同尺度的邻域关系.第二组实验共进行了7种算法的分类性能的比对，分别是数据扰动-γ、数据扰动-CE、数据扰动-NDI、BCS[16]、ESAR[15]、MIFS[18]、PGVNS[19]. 其中，ESAR和BCS是两种集成方法，MIFS和PGVNS是两种适合高维样本的特征选择方法，因为原始MIFS和PGVNS方法是非集成方法，所以从实验数据的公平性起见，对于MIFS和PGVNS的使用，也引入了集成策略，即利用笔者所提出的数据扰动框架进行求解，这也从另外一个侧面展现出所提方法具备即插即用的优势.

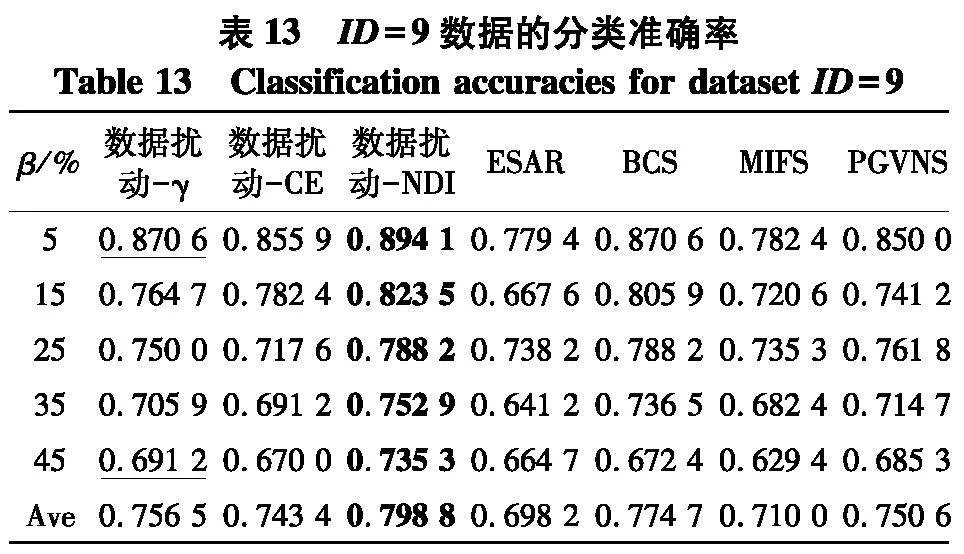
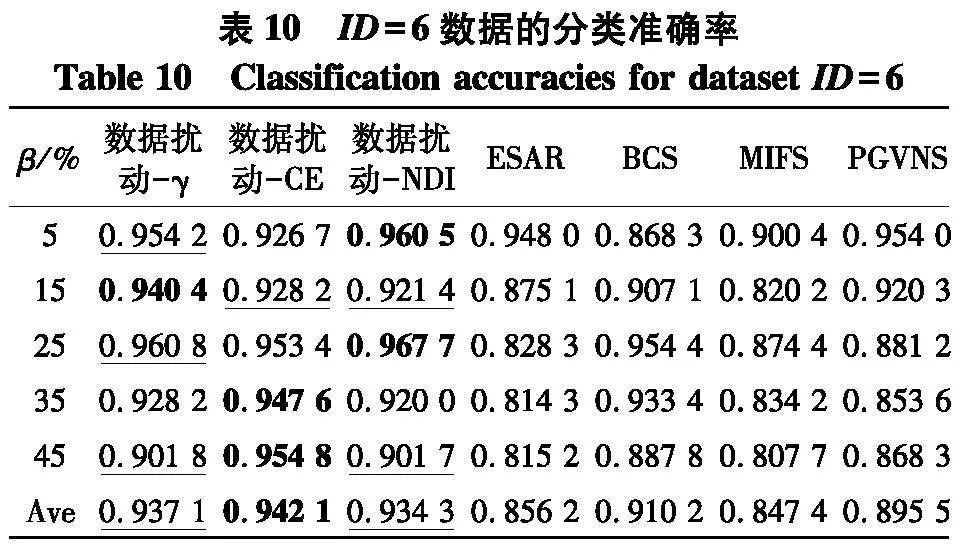
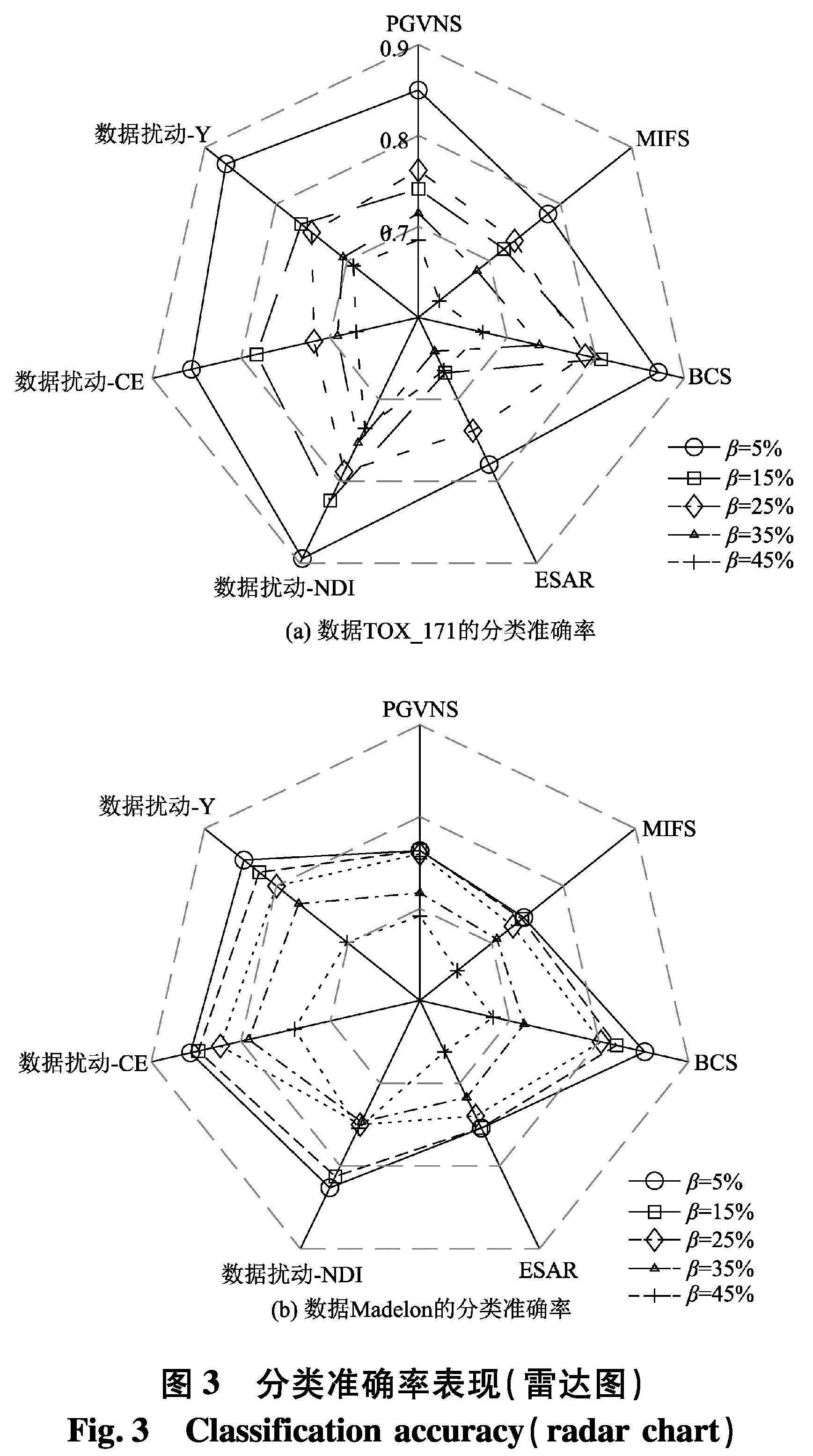
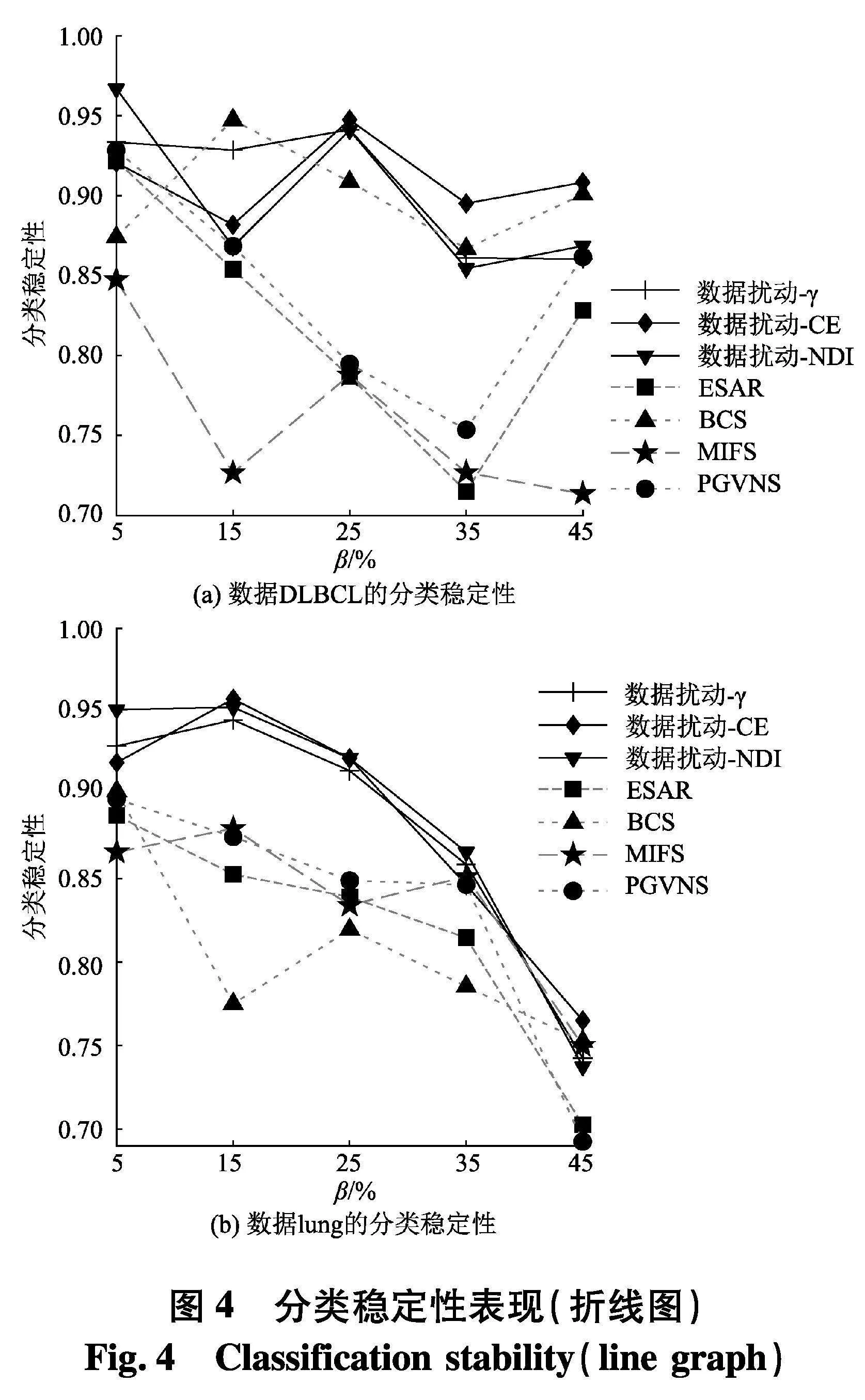
实验使用2个指标来对比不同方法的性能：① PL-kNN分类器所得到的平均分类准确率；② PL-kNN分类器所得到的平均分类稳定性.具体实验结果如表10～13和图3～4.以可视化的形式展现了2个高维数据集上分类准确率表现，图4是2个高维数据集上分类稳定性直观展示.[KH*2D]

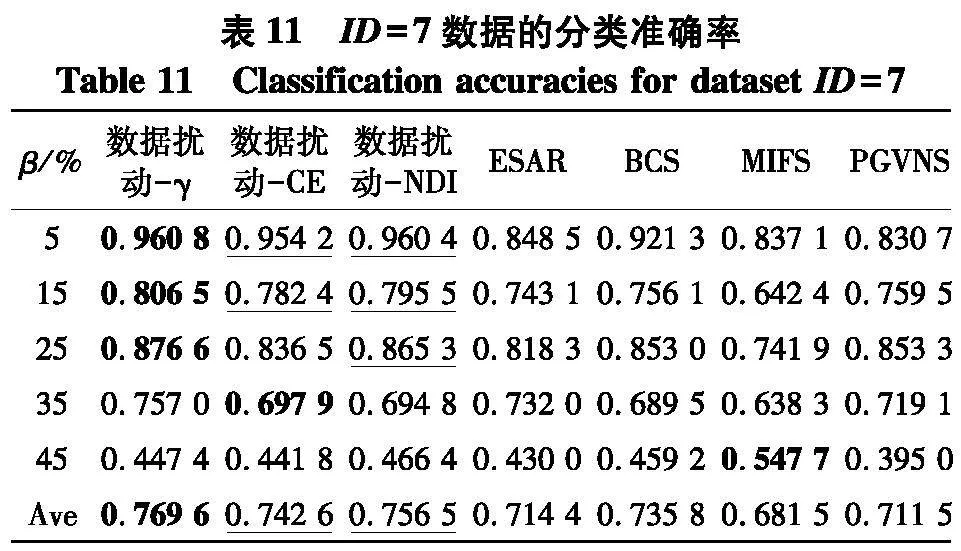
根据表10～13和图3所展示的结果，不难得出以下结论：

（1） 随着百分比β的增大，在分类准确率上这一指标上，7种算法所对应的性能都有下降趋势，这一点从雷达图（图3）中可以清晰地看出，但这种下降并非是严格单调的，例如在表10中，数据扰动-γ方法在噪声比为15%时，所对应的分类准确率为0.940 4，而当噪声比为25%时，分类准确率却达到了0.960 8，在所比对的ESAR、BCS、MIFS和PGVNS算法上都有类似的情形出现，这说明弱标签样本在数据中的比例对于所测试的7种算法对应的分类准确率确实都存在着一定的影响；

（2） 以平均值的视角来看，无论使用哪种度量，采用数据扰动生成多个约简的策略，相较于其它对比算法来说，都能够取得更高的分类准确率，例如在表13中，采用γ、CE和NDI 3种度量的数据扰动策略，分类准确率分别达到了0.756 5、0.745 4和0.798 8，显著优于所对比的另外4种特征选择算法；

（3） 在所比对的4种算法ESAR、BCS、MIFS和PGVNS中，BCS和PGVNS所对应的分类准确率要高于ESAR和MIFS所对应的分类准确率.

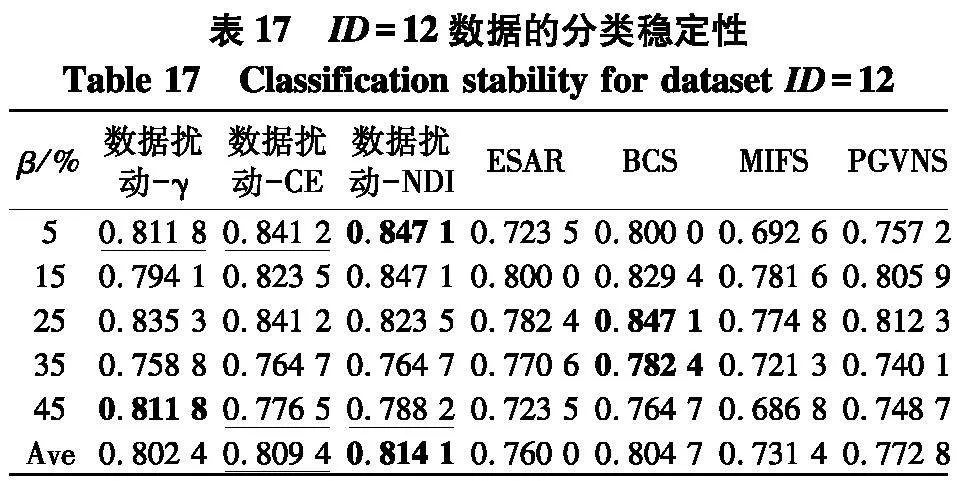
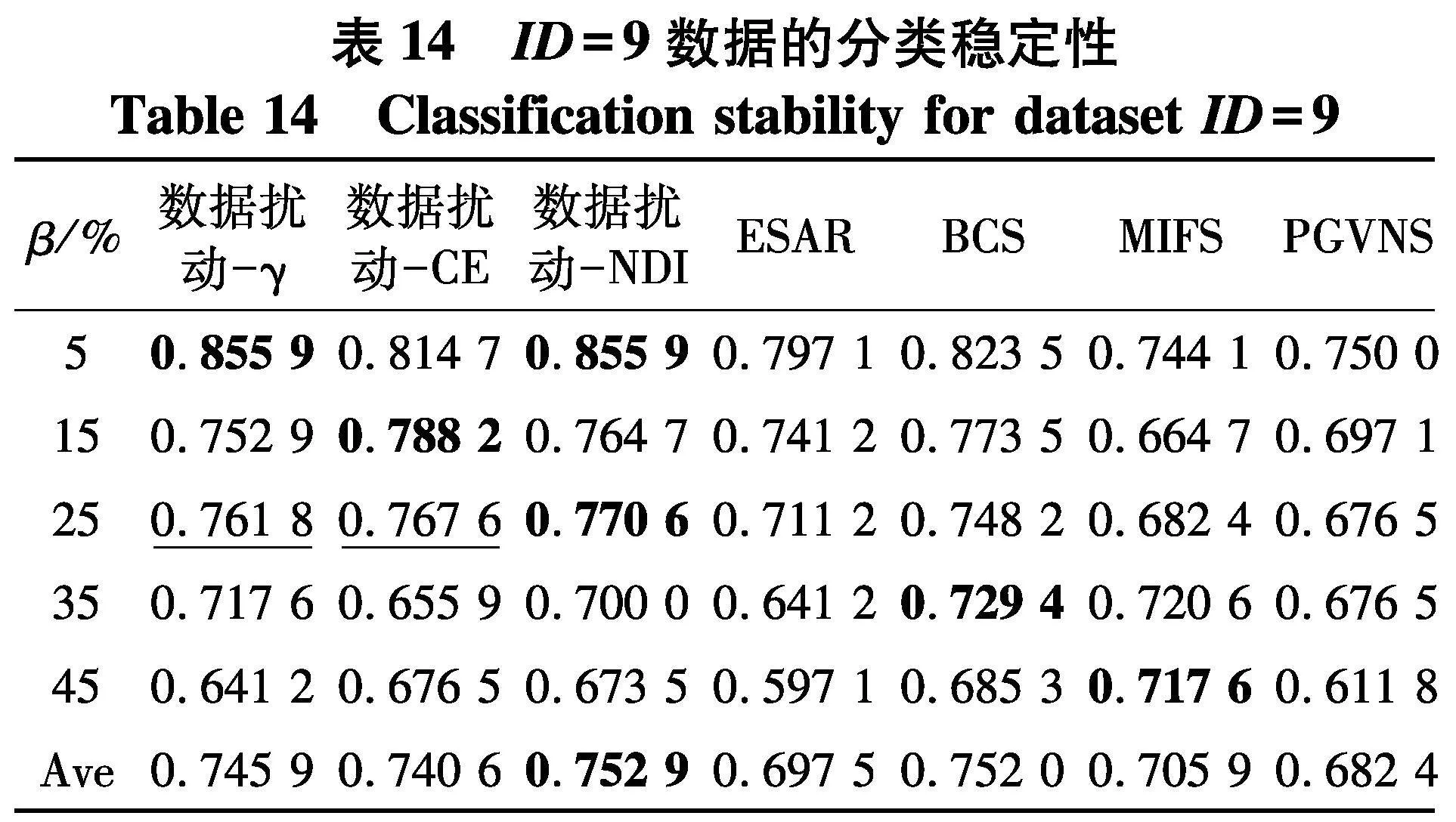
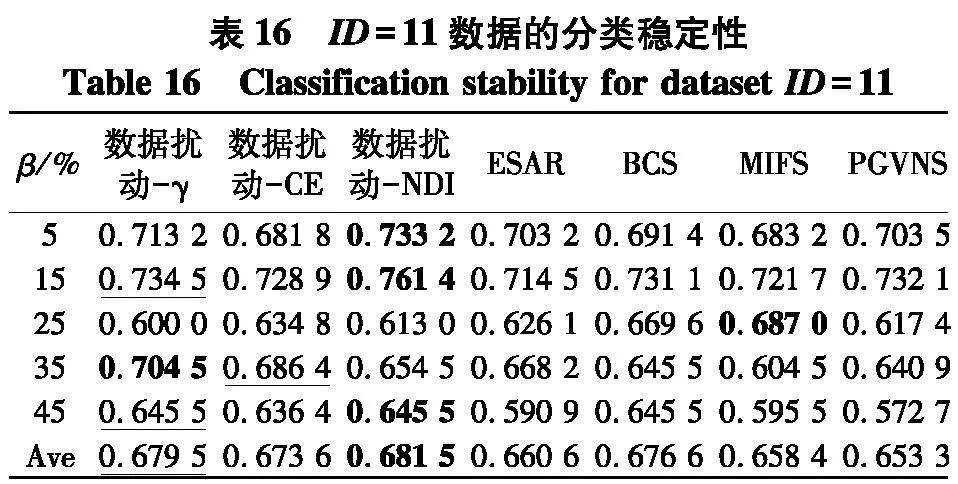
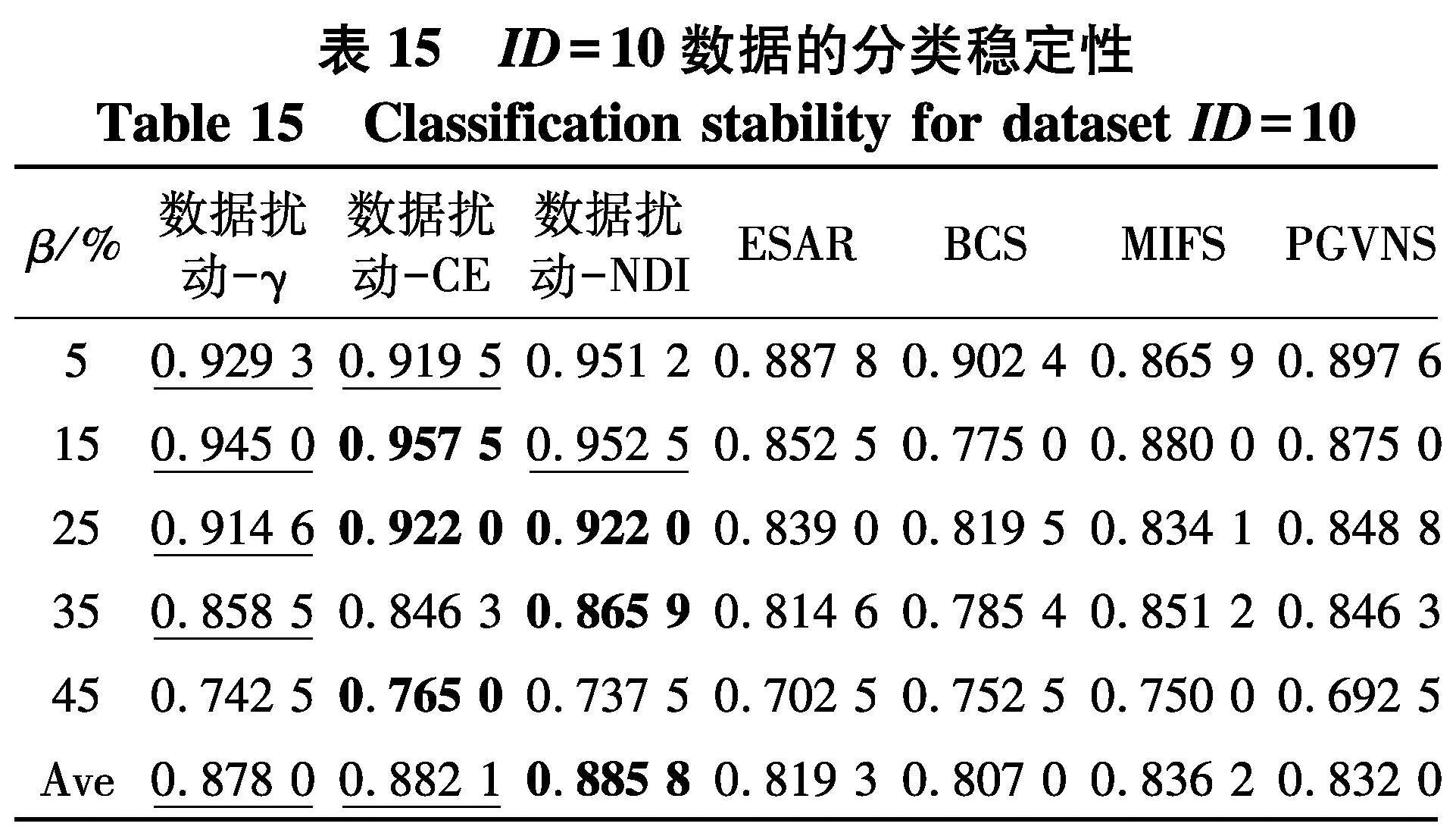
根据表14～17和图4结果，不难得出以下结论：

（1） 随着百分比β的增大，在7种算法所对应分类稳定性上，性能都有下降趋势，但与分类准确率的情形类似，分类稳定性的下降并不是严格单调的，这一点从图4（a）中也可以显著看出，这说明弱标签样本在数据中的比例对于算法进行特征选择求解后对应的分类稳定性也确实存在着一定的影响.

（2） 与分类准确率情形类似，无论使用哪种度量，采用数据扰动生成多个约简的策略，相较于对比方法来说，都能够取得更高的分类稳定性.

4 结论

（1） 首先在邻域粗糙集中，基于弱标签消歧的基础上，引入条件熵、近似质量和鉴别指数度量指标以刻画求得的实例决策系统中的不确定性.

（2） 利用数据扰动，使用扰动数据集和原始数据集求解出的多个不同的特征选择结果，为后续的学习过程提供基础性集成工具.

（3） 提出一种多视角扰动特征选择框架.在UCI和基因库数据集的实验结果验证了文中所提框架的有效性.

（4） 在此基础上，今后将就从扰动的策略上，进一步扩展多视角扰动框架，使扰动框架在多样化的扰动策略中有更强的普适性.把多视角扰动框架推广到更多学习任务中，从而验证多视角扰动框架的普适性.

参考文献（References）

［1］ 巴婧， 陈妍， 杨习贝. 快速求解粒球粗糙集约简的属性划分方法[J]. 南京理工大学学报（自然科学版）， 2021， 45（4）： 394-400.

［2］ 熊菊霞， 吴尽昭， 王秋红. 邻域互信息熵的混合型数据决策代价属性约简[J]. 小型微型计算机系统， 2021， 42（8）：1584-1590.

［3］ CHEN Z， LIU K Y， YANG X B， et al. Random sampling accelerator for attribute reduction[J]. International Journal of Approximate Reasoning， 2022， 140： 75-91.

［4］ LIU K Y， YANG X B， YU H L， et al. Rough set based semi-supervised feature selection via ensemble selector[J]. Knowledge-Based Systems， 2019， 165： 282-296.

［5］ 皋军，黄欣辰，邵星.基于成对约束的半监督选择性聚类集成[J].江苏科技大学学报（自然科学版），2020，34（4）：57-63.

［6］ GONG C， LIU T L， TANG Y Y， et al. A regularization approach for instance-based superset label learning[J]. IEEE Transactions on Cybernetics， 2018， 48（3）： 967-978.

［7］ CHEN C H， PATEL V M， CHELLAPPA R. Learning from ambiguously labeled face images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2018， 40（7）： 1653-1667.

［8］ HLLERMEIER E， BERINGER J. Learning from ambiguously labeled examples[J]. Intelligent Data Analysis， 2006， 10（5）： 419-439.

［9］ NGUYEN N， CARUANA R. Classification with partial labels[C] ∥Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas， Nevada， USA： ACM， 2008： 551-559.

［10］ WANG C Z， HU Q H， WANG X Z， et al. Feature selection based on neighborhood discrimination index[J]. IEEE Transactions on Neural Networks and Learning Systems， 2018， 29： 2986-2999.

［11］ YANG X B， YAO Y Y. Ensembleselector for attribute reduction[J]. Applied Soft Computing，2018，70：1-11.

［12］ CAMPAGNER A， CIUCCI D.Orthopartitions and soft clustering： Soft mutual information measures for clustering validation[J]. Knowledge-Based Systems， 2019， 180： 51-61.

［13］ CAMPAGNER A， CIUCCI D， HLLERMEIER E. Rough set-based feature selection for weakly labeled data[J]. International Journal of Approximate Reasoning， 2021， 136： 150-167.

［14］ ZHANG X， MEI C L， CHEND G， et al. Feature selection in mixed data： A method using a novel fuzzy rough set-based information entropy[J]. Pattern Recognition， 2016， 56： 1-15.

［15］ LIN G P， LIANG J Y， QIAN Y H. Uncertainty measures for multigranulation approximation space[J]. International Journal of Uncertainty， Fuzziness and Knowledge-Based Systems， 2015， 23（3）： 443-458.

［16］ SUN D， ZHANG D Q. Bagging constraint score for feature selection with pairwise constraints[J]. Pattern Recognition， 2010， 43（6）： 2106-2118.

［17］ HU Q H， YU D R， LIU J F， et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information Sciences， 2008， 178（18）： 3577-3594.

［18］ 许行， 张凯， 王文剑. 一种小样本数据的特征选择方法[J]. 计算机研究与发展， 2018， 55（10）： 2321-2330.

［19］ GARCA T M， GMEZ F， MELIN B B， et al. High-dimensional feature selection via feature grouping： A variable neighborhood search approach[J]. Information Sciences， 2016， 326： 102-118.