多粒化粗糙集性质的几个充分条件

张夏苇

(厦门理工学院应用数学学院，福建 厦门 361024)



多粒化粗糙集性质的几个充分条件

张夏苇

(厦门理工学院应用数学学院，福建 厦门 361024)

多粒化粗糙集是Pawlak粗糙集非常重要的一种推广，主要给出当X是C(C′)中任意有限个元素的并集时,乐观多粒化粗糙集(悲观多粒化粗糙集)上下近似对于交并运算的封闭性;得到若X是C′中任意有限个元素的并集，乐观多粒化粗糙集和悲观多粒化粗糙集下近似相等；若～X是C′中任意有限个元素的并集,乐观多粒化粗糙集和悲观多粒化粗糙集上近似相等.

多粒化;粗糙集;等价关系;充分条件

粗糙集是1982年由波兰数学家Pawlak提出的[1]，粗糙集理论是一种新的处理不确定性问题的又一有效的工具.目前，该理论已在诸多领域得到了广泛的应用，如：模式识别，医疗卫生，数据挖掘，模糊分析[2-6].但是，在粗糙集的理论发展过程中，有许多问题是经典的Pawlak粗糙集无法解决的.因此，为了扩展粗糙集理论的应用范围，诸多学者不断地对Pawlak粗糙集进行推广.钱宇华等[7-8]提出了多粒化的粗糙集，从“粒”的角度对Pawlak粗糙集进行了推广.至此，人们对多粒化粗糙集进行了广泛和深入的研究.例如：徐伟华等[9-10]将模糊等理论融入到多粒化粗糙集理论中，提出了多粒化的模糊粗糙集模型，杨习贝等[11]在不完全信息的情形下讨论多粒化粗糙集的性质，并得到诸多有意义的结果.但是悲观多粒化粗糙集和乐观多粒化粗糙集的上下近似的相关性质，它们对于交、并运算是否封闭，如果不封闭，那么在什么条件下会封闭，这些问题都还没有被研究，本文在前人对多粒化粗糙集研究的基础上，对该模型做了进一步的研究，得出了一些结论，丰富和完善了粗糙集的相关理论.

1　预备知识

定义1[1]设(U，R)，R⊆R为U上一个等价关系，对∀X⊆U,则

分别称为子集X关于等价关系R的Pawlak下近似和上近似.

定义2[7-8]设(U，R)为近似空间，R1，R2，…，Rs⊆R为等价关系，对∀X⊆U,则

分别称为子集X关于等价关系R1，R2，…，Rs的乐观多粒化下近似和乐观多粒化上近似.

分别称为子集X关于等价关系R1，R2，…，Rs的悲观多粒化下近似和悲观多粒化上近似.

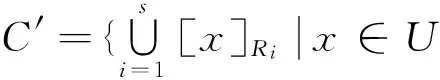
2　乐观多粒化粗糙集的几个充分条件

在文献[7]中给出多粒化粗糙集的如下性质.

定理1[7]设(U，R)为近似空间，R1，R2，…，Rs⊆R为等价关系，对∀x∈U和∀X,Y⊆U，有下列性质：

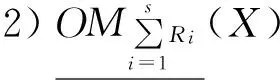
定理2设(U，R)为近似空间，R1，R2，…，Rs为等价关系，对∀X⊆U，有下列性质成立：

证明由定义2及C的构造显然可得.

下面举例对定理2作进一步的说明.

例1设

U={x1,x2,…,x6},U/R1={{x1,x2},{x3},{x4,x6},{x5}}，U/R2={{x1,x3},{x2,x5},{x4},{x6}}，对X1={x3}∪{x2,x5}={x2,x3,x5}，有

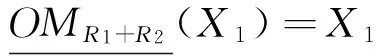
对～X2={x3}∪{x2,x5}={x2,x3,x5}，即X2={x1,x4,x6}，有

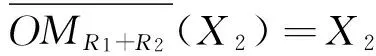
定理3设(U，R)为近似空间，R1，R2，…，Rs为等价关系，∀X,Y⊆U，有下列性质成立：

1)若X∩Y是C中任意有限个元素的并集，则

2)若～(X∪Y)是C中任意有限个元素的并集，则

证明1)“⟹”由定理1显然可得.

2)由定理1和1)可得.

下面举例对定理3进行说明.

例2在例1中令X1={x1,x2,x3,x4},Y1={x3,x4,x5}，则

所以有

令X2={x4},Y2={x5,x6}，则

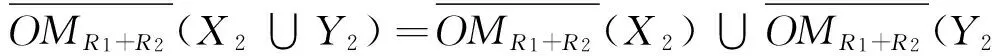
另外还有如下结论.

定理4设(U，R)为近似空间，R1，R2，…，Rs为等价关系，对∀X⊆U，下列性质成立：

1)若X是C中任意有限个元素的并集，则

2)若～X是C中任意有限个元素的并集，则

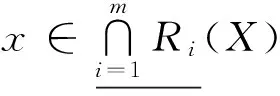
2)类似可证.

下面举例对定理4进行说明.

例3令

U={x1,x2,…,x6},U/R1={{x1,x2,x3},{x4,x5},{x6}},U/R2={{x1,x3,x4,x5},{x2,x6}},

取X1={{x1,x2,x3},{x2,x6}}={x1,x2,x3,x6},则有

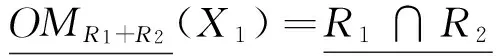
3　悲观多粒化粗糙集的几个充分条件

在文献[8]中给出了悲观多粒化粗糙集的如下性质.

定理5[8]设(U，R)为近似空间，R1，R2，…，Rs⊆R为等价关系，对∀x∈U和∀X、Y⊆U，下列性质成立：

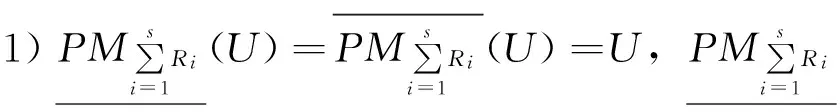
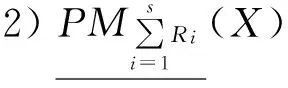
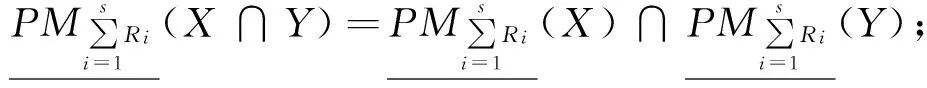
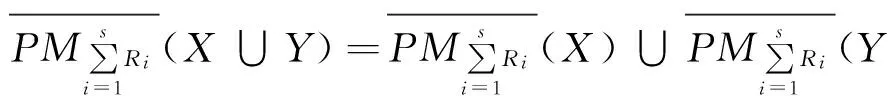
定理6设(U，R)为近似空间，R1，R2，…，Rs⊆R为等价关系，对∀X⊆U，下列性质成立：

1)若X是C′中任意有限个元素的并集，则

2)若～X是C′中任意有限个元素的并集，则

证明1)“⟹”由定理1显然可得.

2)类似可证.

例4由例4，可得C′={{x1,x2,x3},{x1,x2,x5},{x1,x3},{x4,x6},{x2,x5}}，对

X1={{x1,x2,x3}∪{x4,x6}}={x1,x2,x3，x4,x6}，由定义2可得

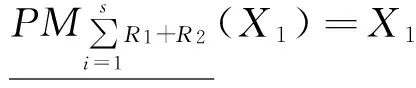
对～X2={x1,x2,x3}∪{x2,x5}={x1,x2,x3,x5}，即X2={x4,x6}，由定义2可得

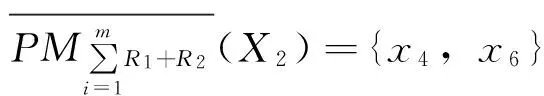
4　乐观多粒化粗糙集与悲观多粒化粗糙集之间的关系

由定义2显然可得：对∀X⊆U，

定理7对∀X⊆U，若X是C′中任意有限个元素的并集，则有

证明由定理2，定理3和定义2显然可得.

定理8对∀X⊆U，若～X是C′中任意有限个元素的并集，则有

证明由定理2，定理3和定义2显然可得.

5　结语

多粒化粗糙集模型是Pawlak粗糙集一种非常重要的推广形式，目前仍是粗糙集领域的一个研究热点.Pawlak粗糙集有着良好的性质，但是多粒化粗糙集有很多性质却并不满足，例如多粒化粗糙集并不满足粒度性，悲观多粒化粗糙集不满足幂等性，乐观多粒化粗糙集也不满足蕴含性等等.本文则结合相应的例子分别给出了使上述条件成立的充分条件，那就是X或～X需要满足是C(C′)中任意有限个元素的并集，这些结论的取得丰富了粗糙集的有关理论，扩大了多粒化粗糙集的应用范畴.

[1]PAWLAK Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.

[2]ANANTHANARAYANAV S,NARASIMHA M M,SUBRAMANIAN D K.Tree structure for efficient data mining using rough sets[J].Pattern Recognition Letter,2003,24(6):851-862.

[3]GRZY MALA-BUSSEI,SIDDHAYE S.Rough sets approach to rule induction from incomplete data[C]//Proceedings of 10th International Conference on Information Proceeding and Management of Uncertainty in Knowledge-Based Systems,2004，2:923-930.

[4]JEON G,KIM D,JEONG J.Rough sets attributes reduction based expert system in interlaced video sequences[J].IEEE Transactions on Consumer Electronics,2006，52(4):1 348-1 355.

[5]LI J H,MEI C L,LV Y J.Knowledge reduction in real decision formal contexts[J].Information Sciences,2012，189:191-207.

[6]SWINIARSKI R W,SKOWRON A.Rough set method in feature selection and recognition[J].Pattern Recognition Letter,2003，24(6):833-849.

[7]QIAN Y H,LIANG J Y,YAO Y Y,et al.MGRS:a multi-granulation rough set[J].Information Sciences，2010，180(6):949-970.

[8]QIAN Y H,LIANG J Y,WEI W.Pessimistic rough decision[C]//Second International Workshop on Rough Sets Theory.Zhoushan:[s.n.],2004，12：440-449.

[9]XU W H,WANG Q R,LUO S Q.Multi-granulation fuzzy rough sets[J].Journal of Intelligent and Fuzzy Systems，2014，26:1 323-1 340.

[10]XU W H,WANG Q R,ZHANG X T.Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space[J].International Journal of Fuzzy Systems，2011，13(4):246-259.

[11]YANG X B,SONG X N,DOU H L,et al.Multi-granulation rough set:from crisp to fuzzy case[J].Ann Fuzzy Math Information,2011,1(1):55-70.

(责任编辑李宁)

Several Sufficient Conditions on Multi-granulation Rough Sets

ZHANG Xiawei

(School of Applied Mathematics,Xiamen University of Technology,Xiamen 361024,China)

Multi-granulation Rough Set is an important extension of Pawlak rough set,and we mainly give properties on union and intersection of upper and lower approximation of optimistic(pessimistic)multi-granulation rough sets when X is the union of finite elements of C(C′).Finally,we show that when X is the union of finite elements ofC′,the lower approximation of optimistic multi-granulation rough sets and pessimistic multi-granulation rough are equivalent;Same result to the upper approximation of optimistic multi-granulation rough sets and pessimistic multi-granulation rough when～X is the union of finite elements of C′.

multi-granulation;rough set;equivalent relation;sufficient condition

2016-01-08

2016-04-22

国家自然科学基金项目(11426192)

张夏苇(1981-)，女，讲师，硕士，研究方向为人工智能、粗糙集的研究.E-mail:xwzhang@xmut.edu.cn

O23；TP18

A

1673-4432(2016)03-0106-06