基于网格搜索与支持向量回归的粉煤灰混凝土抗压强度预测研究

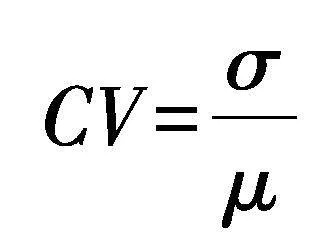
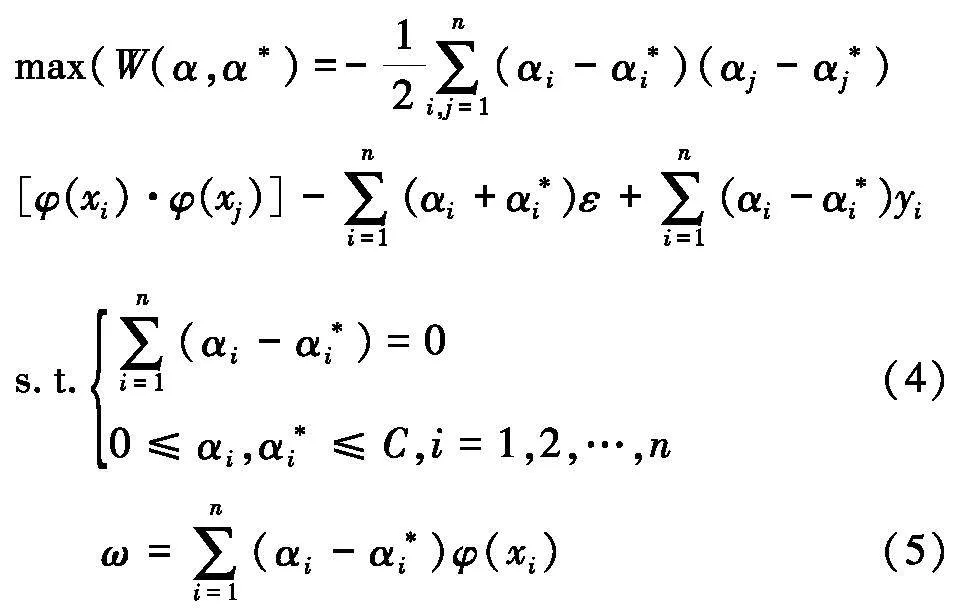
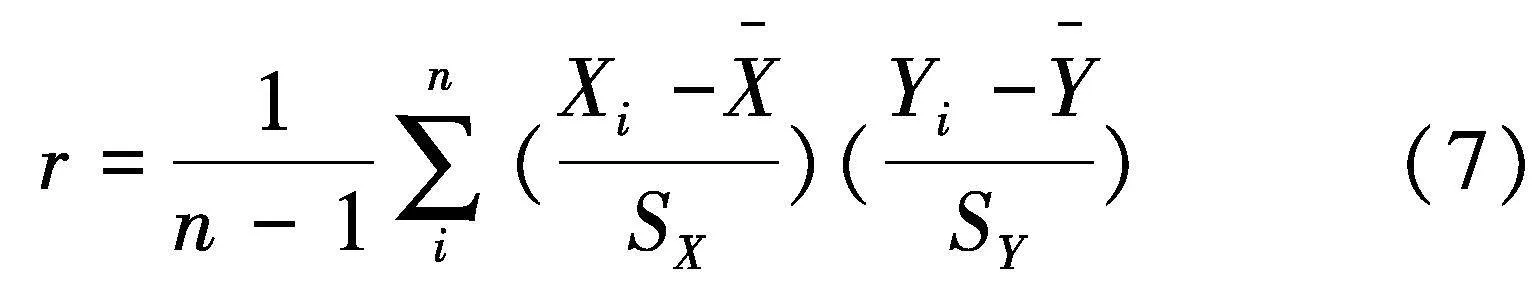
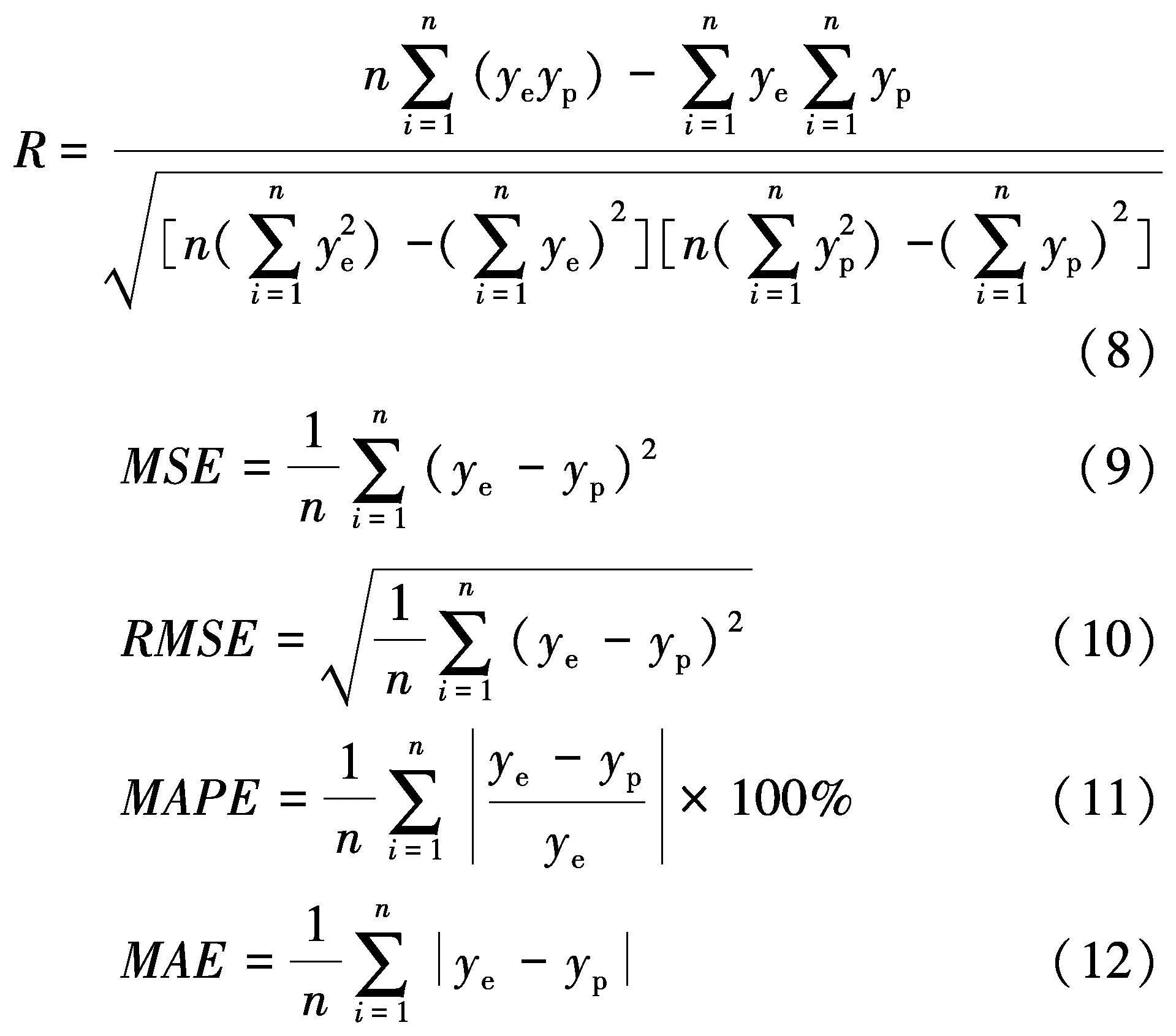
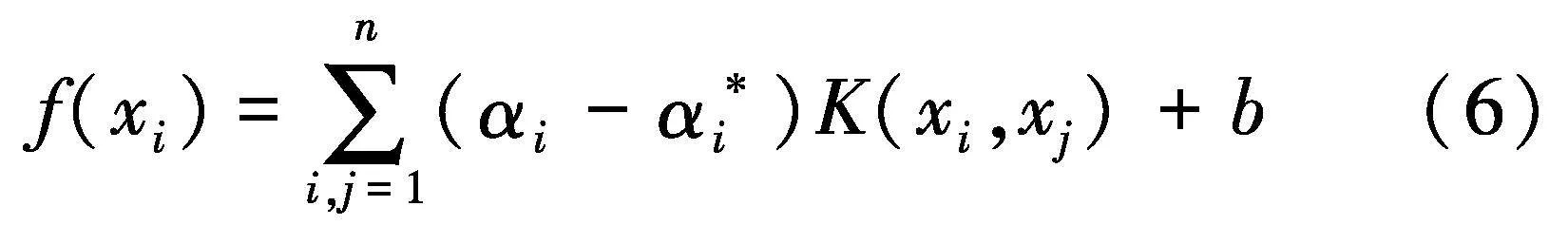
摘 要： 支持向量回归（support vector regression， SVR）已被应用于混凝土力学性能的预测，但其超参数的选择一直是影响预测精度的关键因素.本研究提出一种结合网格搜索方法（grid search， GS）和支持向量回归模型的混合机器学习，即GS-SVR模型，用于混凝土抗压强度预测和敏感性分析.该混合模型在从文献中检索到的98个数据集上进行了训练和测试，并在相同的数据集下将模型与原始SVR模型进行性能比较.所获得R为0.981，MSE为3.44，RMSE为1.85，MAE为1.17，MAPE为0.05.研究结果表明：所提出的GS-SVR模型可以作为后续相关研究中抗压强度预测的一个候选方法.此外，还开发了一个图形用户界面（GUI），以便在进行大量的实验室或现场工作之前，能够提供一些初步的估计结果.最后，分析了随机环境下各变量对抗压强度的影响.

关键词： 粉煤灰混凝土；抗压强度；支持向量回归；机器学习；敏感性分析

中图分类号：TU528"" 文献标志码：A"""" 文章编号：1673-4807（2024）02-073-07

Prediction of the compressive strength of fly ash concrete based onhybridizing grid search and support vector regression

Abstract：Support vector regression （SVR） has been applied to the prediction of mechanical properties of concrete， but the selection of its hyper-parameters has been a key factor affecting the prediction accuracy. A hybrid machine learning combines the SVR model and grid search （GS）， namely the GS-SVR model， is proposed to predict the compressive strength of concrete and to analyze its sensitivity in this work. The hybrid model is trained and tested on a total of 98 data sets retrieved from literature， and the model performance is compared with that of the original SVR model on the same data sets. The results obtained for R， MSE， RMSE， MAE and MAPE are 0.981， 3.44， 1.85， 1.17 and 0.05， respectively， demonstrating that the GS-SVR model proposed can be a candidate method for compressive strength prediction in subsequent related studies. Additionally， a graphical user interface （GUI） is developed to conveniently provide some initial estimates of the outcomes before performing extensive laboratory or fieldwork. Finally， the effect of each variable on the compressive strength in a random environment is analyzed.

Key words：fly ash concrete， compressive strength， support vector regression， machine learning， sensitivity analysis[ZK）]

由于混凝土是一种非均质且复杂的混合物，保证其抗压强度的预测精度较为困难，传统的混凝土强度预测方法主要是基于线性或非线性回归方程的统计分析，由于组成混凝土的成分复杂，在预测其抗压强度时，很难将每种成分与抗压强度间建立一个准确的方程.为了准确预估混凝土的力学性能，人工神经网络（ANN）、支持向量机（SVM）、多元线性回归（MLR）和随机森林（RF）和深度学习（DL）等机器学习技术逐渐应用于混凝土抗压强度的预测[1-8].

文献[9]针对试验收集的56份数据样本中建立一种经过特征筛选的抗压强度随机森林预测模型，利用优化后的输入指标进行强度预测，得出随机森林模型的预测精度较高（R2=0.969 09），误差较小（RMSE=0.014 922）.文献[10]通过建立遗传算法优化的BP神经网络预测模型（GA-BP）预测多孔混凝土的抗压强度值，并与线性回归方程抗压强度计算值进行比较，发现GA-BP神经网络模型计算精度与离散性更优.文献[11]通过建立BP神经网络模型预测混凝土7、28 d抗压强度，得出BP神经网络具有很强的非线性映射能力，模型预测计算的7、28 d强度值和实际值的相关系数达到了0.980 31、0.955 64，预测精度高.文献[12]提出了一种基于相关向量机的再生保温混凝土抗压强度预测模型，通过对少量样本的学习，建立各影响因素与抗压强度的非线性映射关系对仅知道影响因素的预测样本进行抗压强度值精准预测.文献[13]将粉煤灰骨料分次替代30%粗集料作为内固化剂，研制了M30级自养护混凝土，采用3种不同算法预测和验证混凝土特征强度参数，发现决策树回归法预测混凝土强度特性拟合回归曲线误差最小.文献[14]从文献中收集了515个带有回收骨料的自密实混凝土混合设计样本，使用机器学习技术创建模型用于训练、验证和测试其抗压强度，通过敏感性分析和误差评估来选择最佳的机器学习方法.文献[15]利用多元多元回归（MMR）、支持向量机（SVM）、高斯过程回归（GPR）和回归树（RT）等机器学习模型对468个立方体混凝土样本的混凝土抗压强度进行预测，发现GPR/SVM和RT在MMR模型上使用回弹锤记录获得了最准确的抗压强度模型预测指标.

通过查阅相关文献可知，机器学习模型能够通过提取输入和输出变量之间的未知关系，实现对多维非线性关系的捕捉和映射，其拟合精度高于传统的经验公式[16]，然而这些模型常常需要不断调整参数才能获得更好的指标性能，正如支持向量回归（SVR）模型，其超参数的选择是影响预测结果的重要因素之一.由于单一的SVR模型的拟合精度比较有限，故提出基于网格搜索方法（GS）和支持向量回归（SVR）的组合机器学习模型，基于该模型，研究了各个变量的随机变化对抗压强度的影响，作为混凝土混合设计和强度预测的参考和指导.

1 试验方法

1.1 支持向量回归

支持向量回归（SVR）的目标是在n维空间中找到一个对所有样本点进行明确分类的回归超平面，并拟合出使所有样本点与这个回归超平面的总方差最小的线性回归方程.针对一个样本训练集 E={（xi，yi）i=1，2，…，n}，xi∈Rn，yi∈R.在Rn上探测到一个函数f（xi），使得yi=f（xi），对于任何输入x，总有一个相应的y值，这样的函数f（xi）被称为回归函数，f（xi）可以被描述如式（1），其中ω∈Rn是权重向量，φ（xi）是一个非线性算子，是将原始数据映射到更高维的空间，b是一个n维列向量，是函数f（xi）的偏置.

利用式（3）的Lagrange乘子，引入拉格朗日函数以获得其对偶形式.

此时，优化的核心是首先确定特征空间，并在该空间中找到满足条件的最平函数，然后用该函数解决非线性问题.为此，核心函数K（xi，xj）=φ（xi）·φ（xj）被引入.这时的回归拟合函数为：

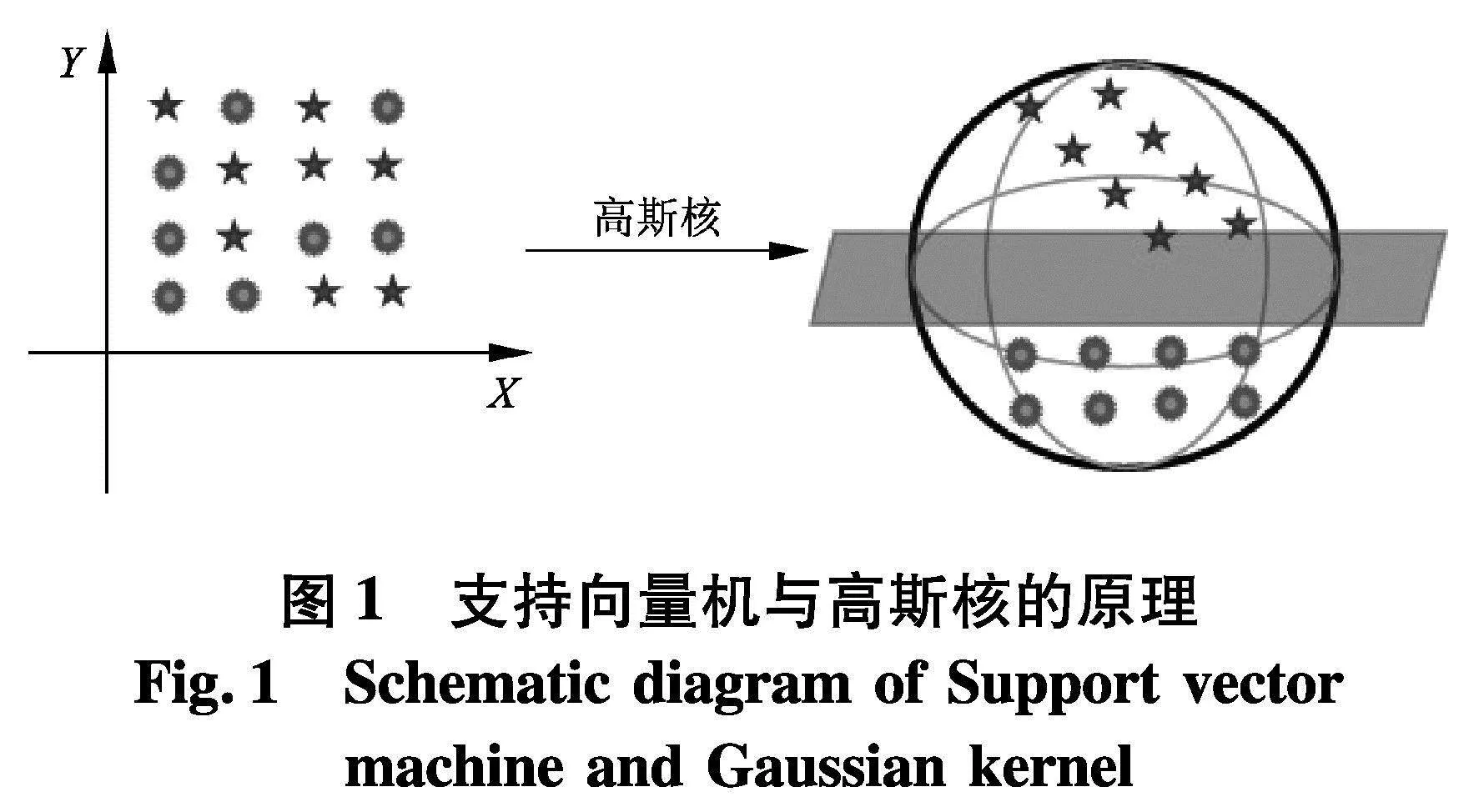
核函数有很多选择，文中选择常用的RBF函数，如图1.

1.2 网格搜索法

众所周知，对于同一问题，不同机器学习算法的性能存在不同程度的差异，而超参数优化对SVR算法的性能也起着至关重要的作用，在实践中通常需要不断调整超参数的值，最终选择最佳的超参数组合[17].

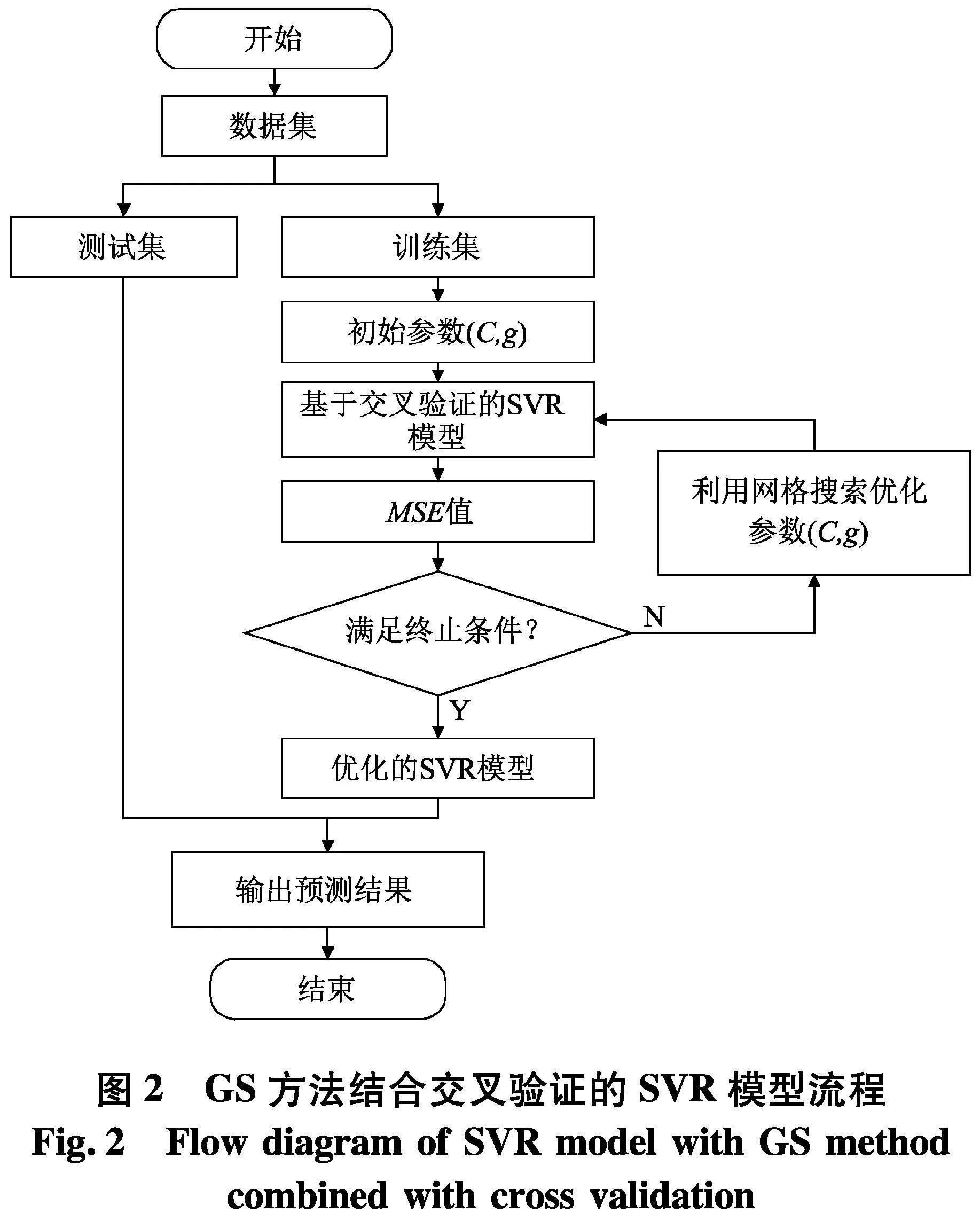
网格搜索法（GS）是指定参数值的一种穷举搜索方法，通过将估计函数的参数通过交叉验证的方法进行优化来得到最优的学习算法.针对所有的候选参数，GS方法可以通过循环迭代的方法计算评估每个参数组合对模型性能的影响，从而解决最佳超参数组合问题.超参数选择流程如图2.

2 数据样本描述

2.1 输入与输出变量

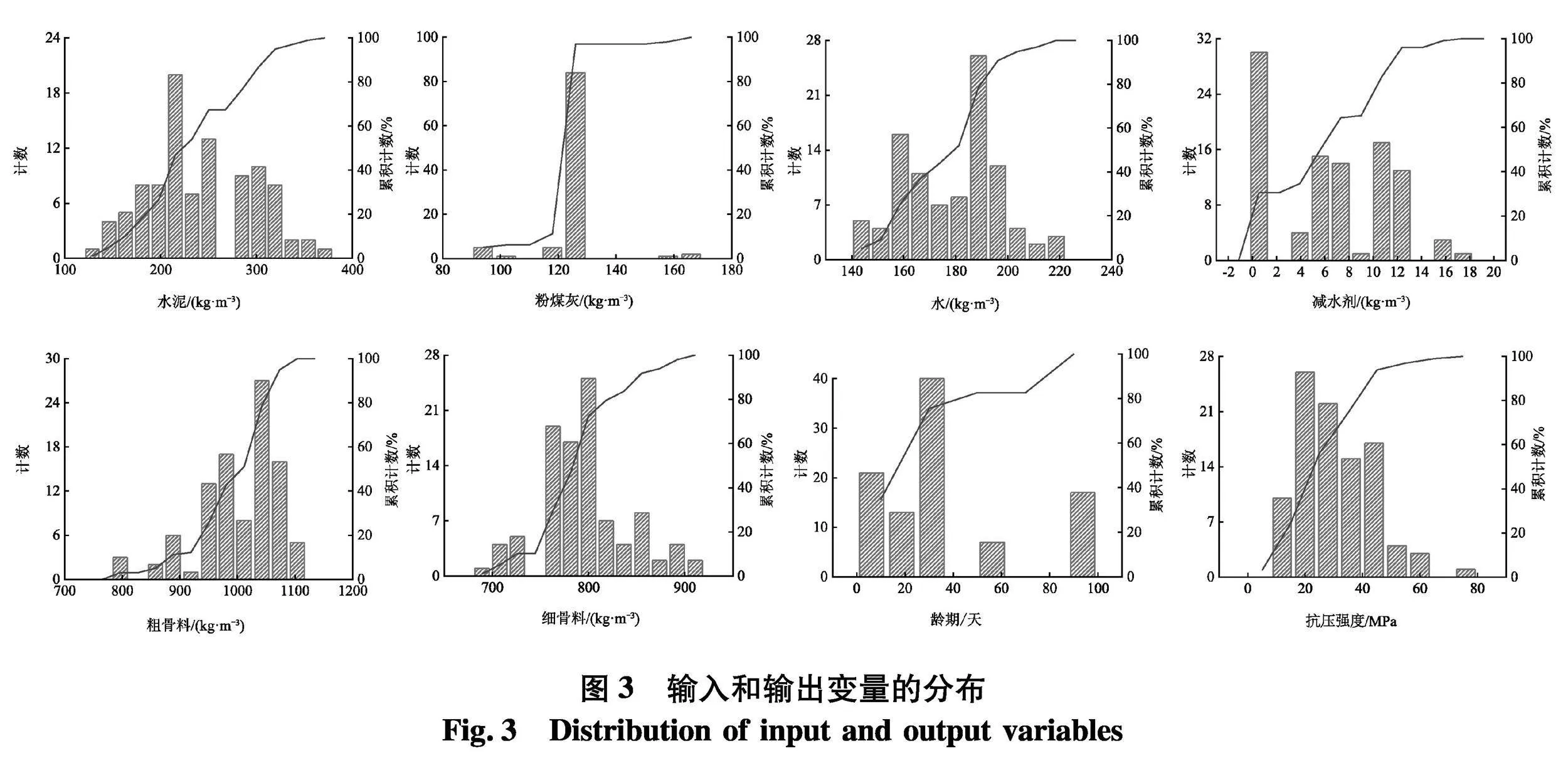
在这项研究中，从文献[18]中检索了98组数

据，每组数据的输入变量为粉煤灰混凝土的6种成分：水泥、粉煤灰、水、减水剂、粗骨料、细骨料以及龄期，输出变量为其抗压强度.输入变量和输出变量的统计特征如表1，其分布情况如图3，根据相关统计特征可知，无论是训练集或是测试集，当输入变量采用不同的组合方式时，其输出变量抗压强度变化幅度也较大，如训练集抗压强度在9.49～72.11 MPa区间变化，这就涉及各个输入变量之间的相关性对输出变量影响问题.

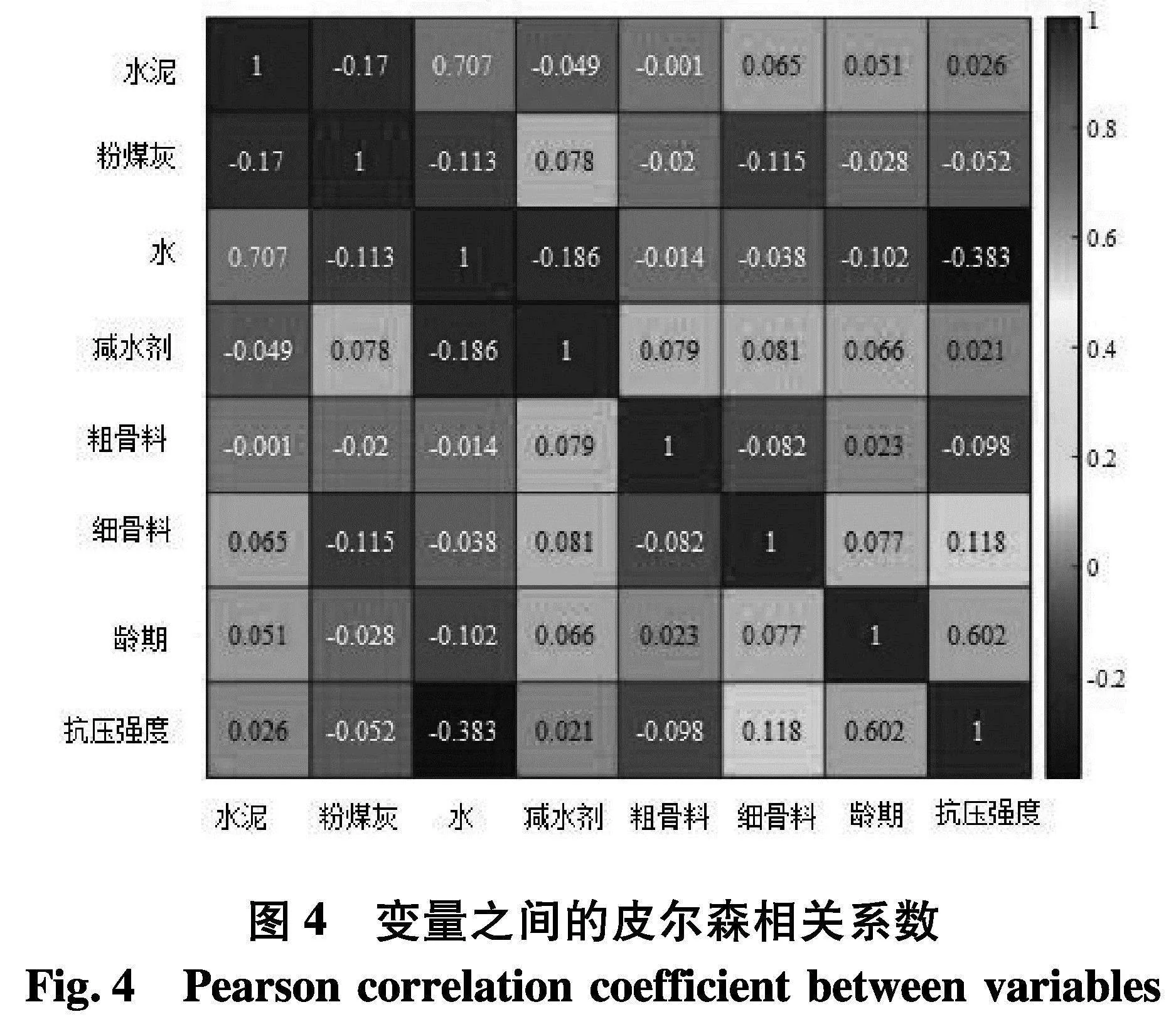
两变量间的相关性可用许多统计值来衡量，最常用的是皮尔森相关系数，皮尔森相关系数r能够反映两个变量的线性相关程度，见式（7），其中n为样本量，r的绝对值越大表明变量之间相关性越强，SX，SY为标准差.输入参数水泥、粉煤灰、水、减水剂、粗集料、细集料、龄期与输出参数抗压强度相互之间的皮尔森相关系数如图4，在使用的98组样本集中，7个输入变量和抗压强度之间的皮尔森相关系数均较小，这表明混凝土抗压强度和这些输入参数之间的线性相关都很弱，存在不明确的非线性关系.

2.2 评价指标

现引入5个评价参数用以比较SVR模型和GS-SVR模型的预测性能，即线性相关系数（R）、均方误差（MSE）、平均根误差（RMSE）、平均绝对百分比误差（MAPE）和平均绝对误差（MAE） [19].参数计算方法如下：

式中：n是样本的数量，ye是粉煤灰混凝土抗压强度实验值，yp是预测值.当线性相关系数R越接近1，则变量间线性相关程度越高，其他4个误差参数越接近0时，模型的预测精度就越高.

3 模型预测结果

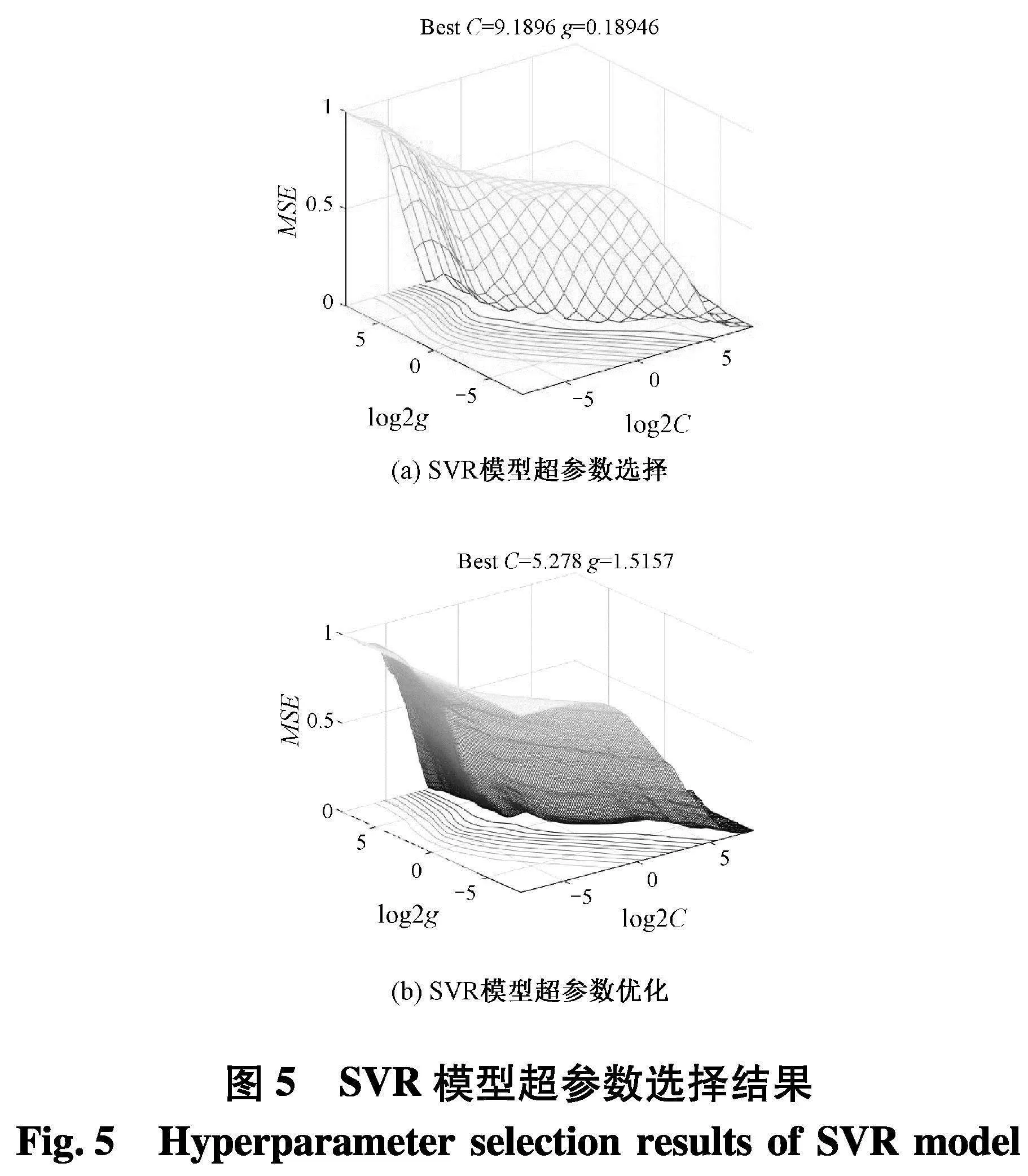
最初，GS法被用于选择SVR中的超参数.对于GS-SVR模型，C和g是在[2-8，28]的指数网格中搜索的，步长为20.1.参数的演变情况如图5.该模型采用10倍交叉验证法进行训练.

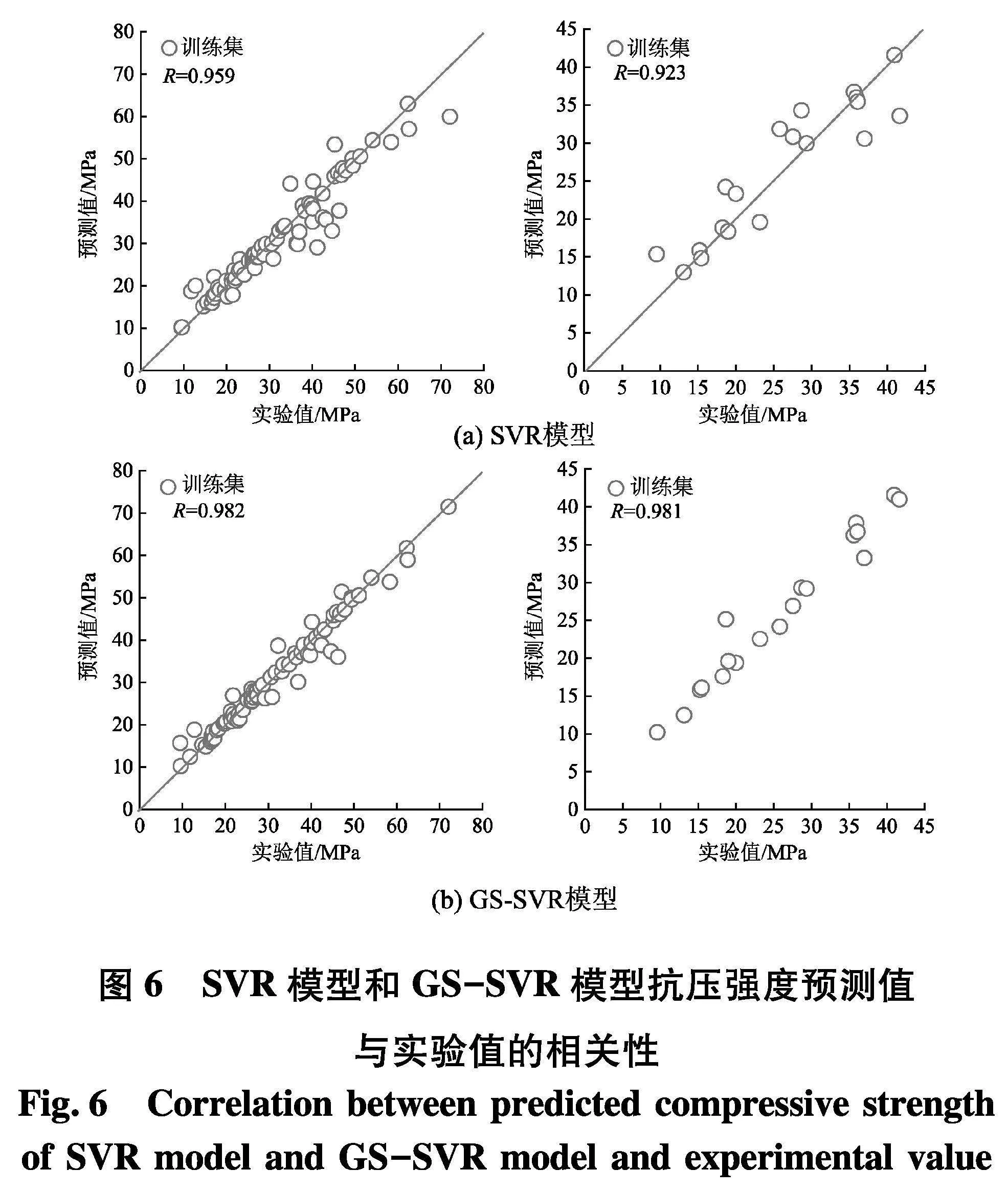
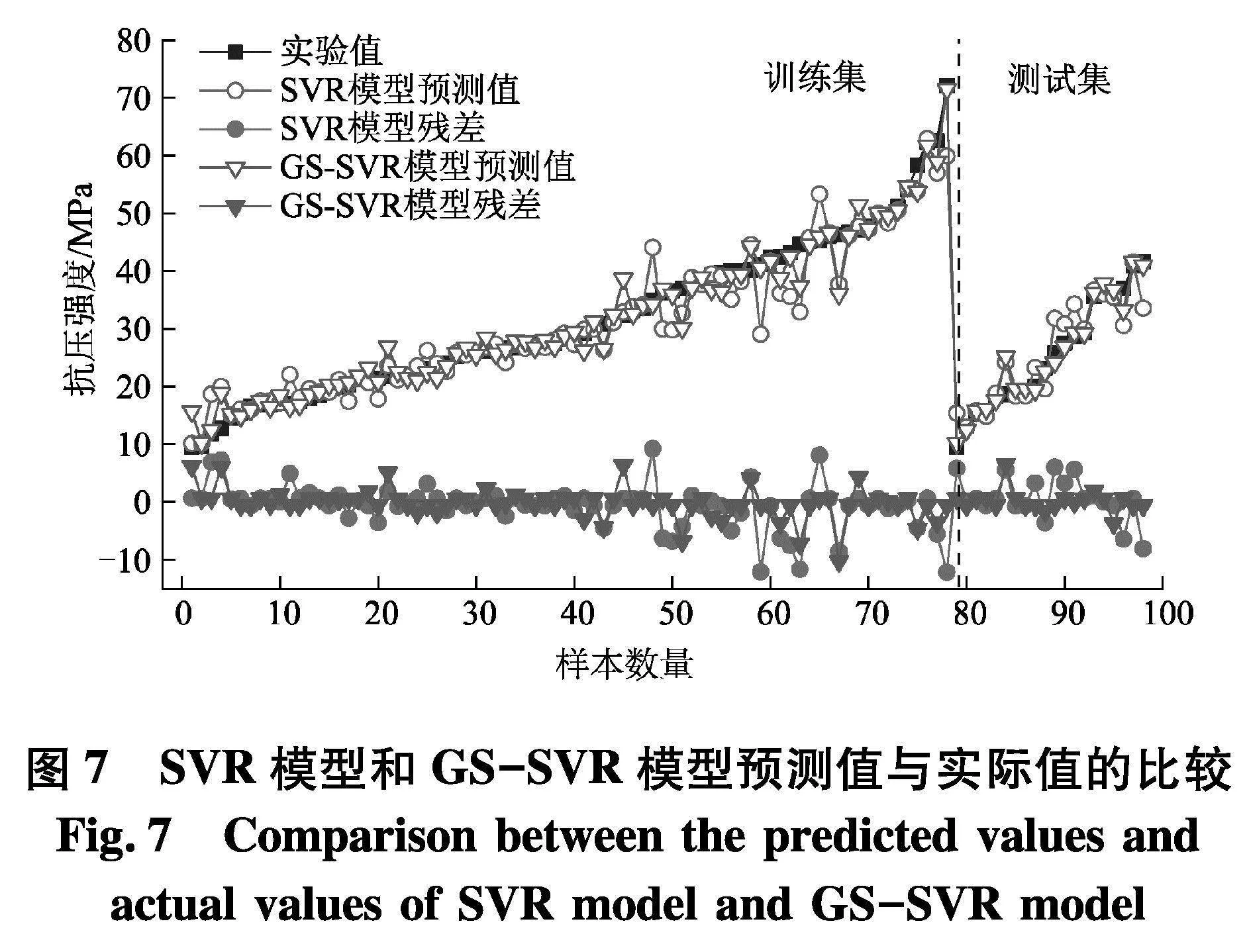
为了比较原始SVR模型和GS-SVR模型的预测性能，采用同一训练集和测试集对两种模型进行测试，计算得到SVR模型训练集和测试集中预测值和实验值相关性系数分别为0.959和0.923，GS-SVR模型相应相关性系数分别为0.982和0.981，均比SVR模型高，且训练集和测试集的相关系数R都超过0.98；SVR模型和GS-SVR模型预测值和实验值的预测结果如图6.

训练集和测试集离散点越靠近对角线则表明预测结果越精确，可以清楚地看到，GS-SVR模型预测结果数据点沿对角线分布更加密集，表明GS-SVR模型对于混凝土抗压强度预测值与实验值的匹配度更好，预测精度更高.

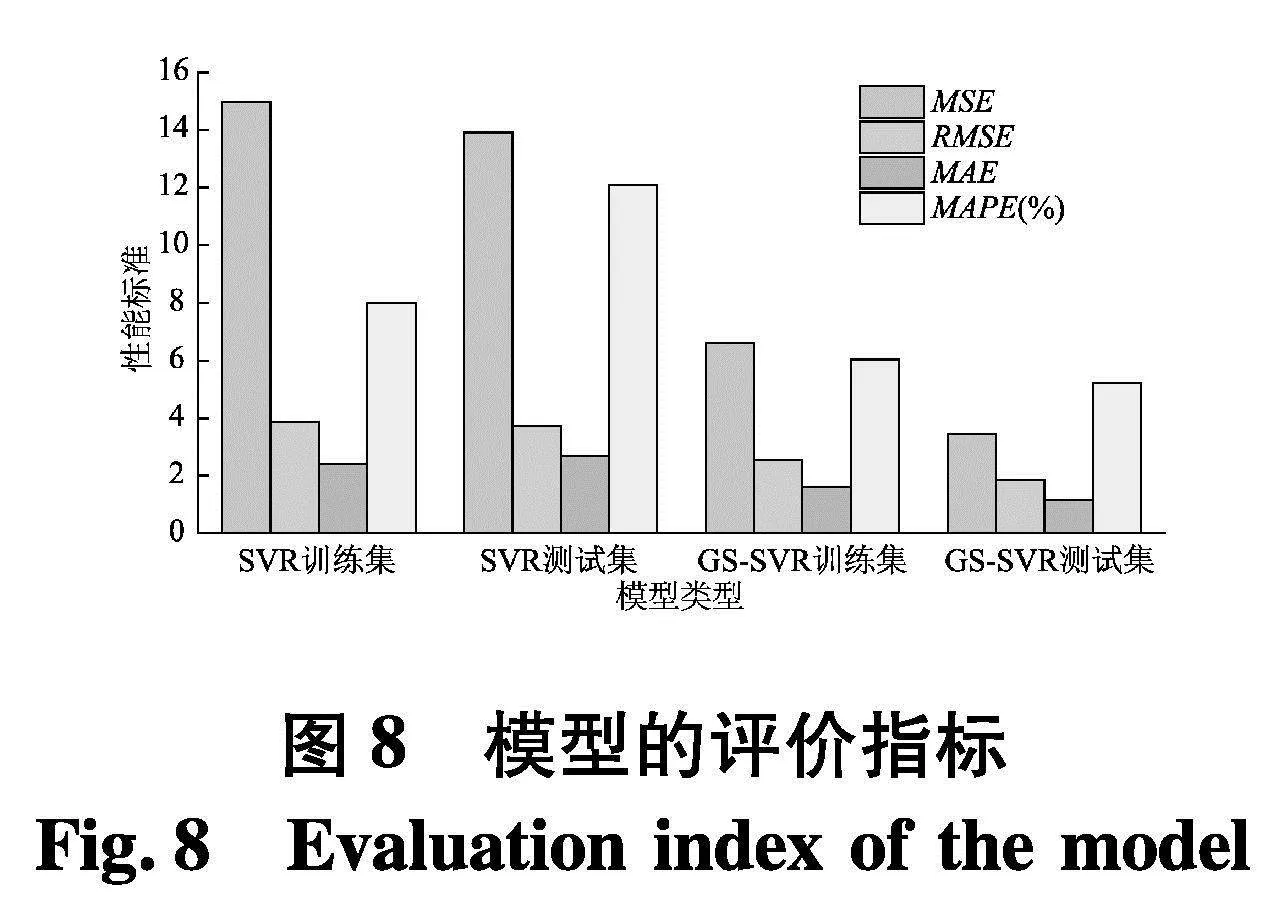
出于比较和评估的目的，图7更详细地显示了训练和测试集的预测值和实验值，相比SVR模型，GS-SVR模型在每个样本点的预测值与实验值更加吻合，显示了GS-SVR模型能够更准确的捕捉7个输入变量和抗压强度之间复杂的非线性关系.两种模型在训练集和测试集的误差参数如图8，可知GS-SVR模型的4个误差指标明显小于SVR模型，其中SVR模型测试集的4个误差指标MSE、RMSE、MAPE和MAE分别为13.8%、3.8%、2.7%、12.1%，GS-SVR模型分别为3.3%、1.9%、1.0%、3.2%，误差分别是SVR模型的0.24倍、0.5倍、0.37倍、0.26倍，从这两组数据中可以明显看出GS-SVR模型具有更好的准确性和泛化能力.

4 灵敏度分析

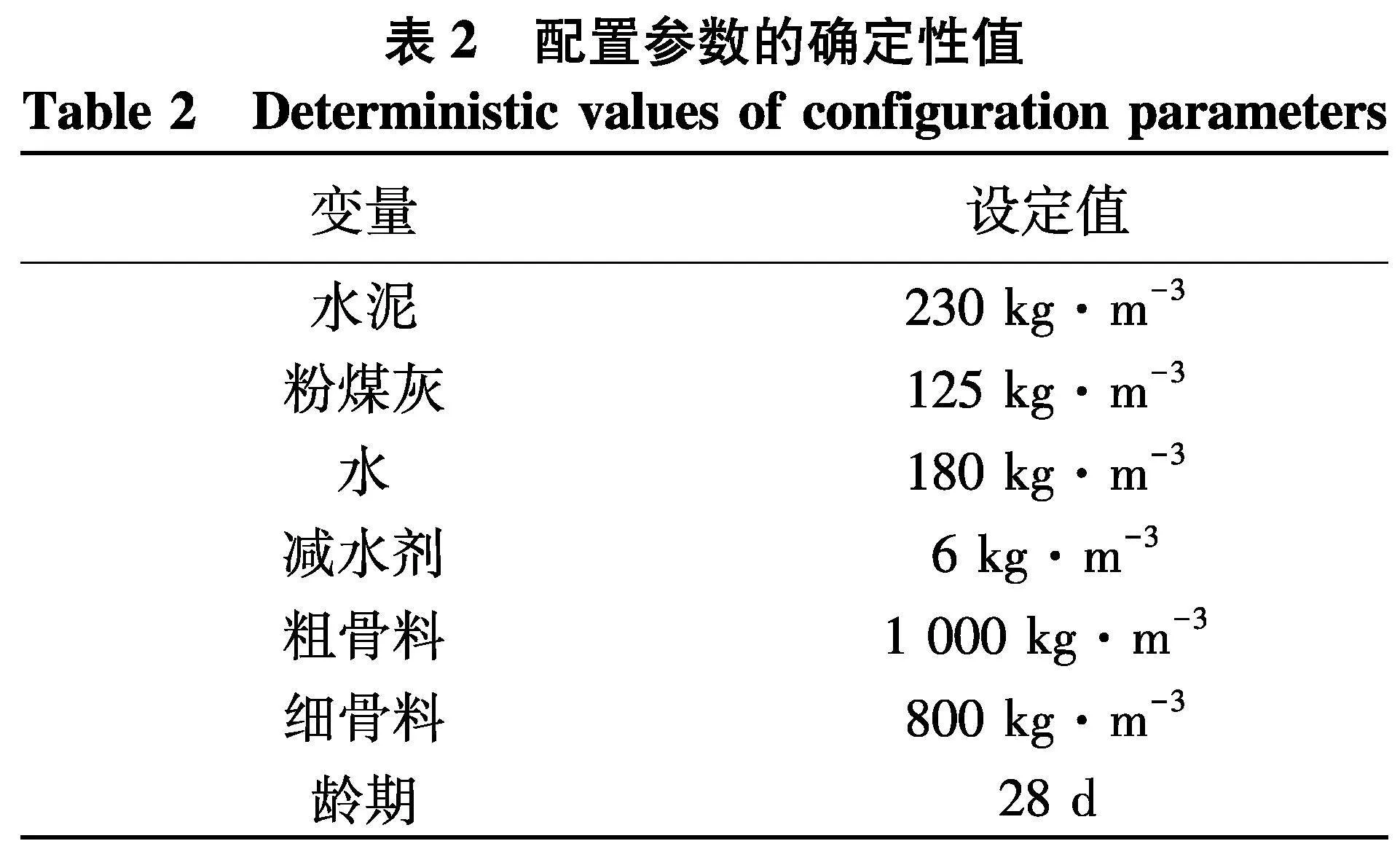
第3节的模型结果表明，抗压强度取决于由六种成分和龄期组成的输入向量.然而，这些变量在随机环境中几乎没有确定的值，这种不确定性可能导致混凝土抗压强度的预测值和实际值的偏差.因此，本节重点讨论各输入变量的随机变化程度对抗压强度的影响.根据表1中的数据集的统计特征，表2中列出了一组具有确定性配置的输入向量.

输入变量被假定为处于3种不同的随机程度值S0=（0.05，0.1，0.15）.在每个随机性设置中，使用MATLAB生成104个样本.为了量化和比较对输出变量的影响程度，随机输入对抗压强度的敏感性定义如下[20]：

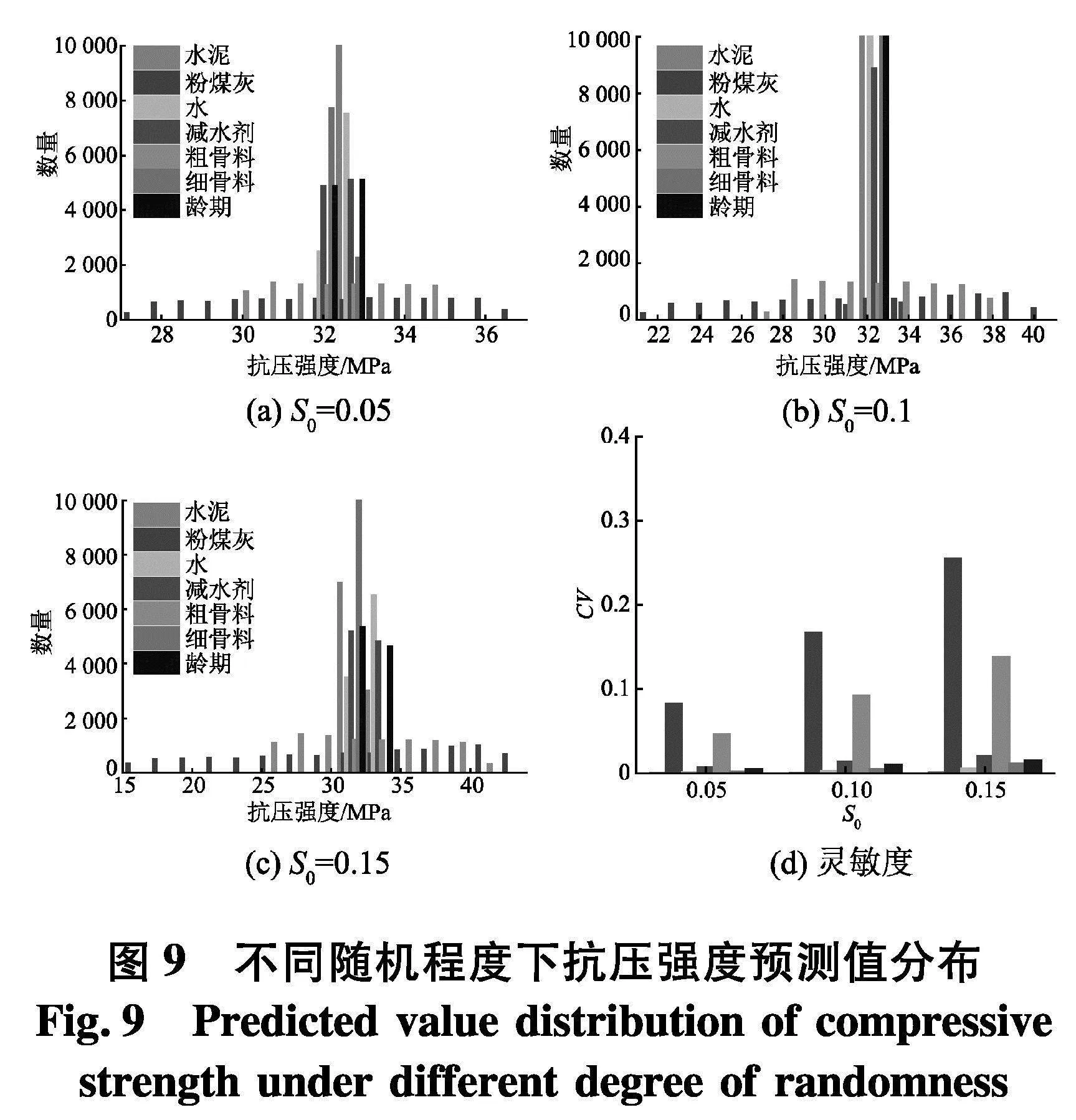
式中：σ和μ分别是抗压强度的标准差和平均值.3种随机性设置下的抗压强度分布如图9.

结果表明，随着随机性S0的增加，混凝土抗压强度对粉煤灰和粗骨料等相关变量的敏感性随之提高，如图9.此外，在影响混凝土抗压强度的7个变量中，水泥、水和细骨料对混凝土抗压强度预测较为稳定，而粉煤灰和粗骨料导致抗压强度预测值的分布更加离散，其中粉煤灰对抗压强度预测值的不确定性影响最大，在粉煤灰混凝土配合比设计时应该重点关注随机环境下粉煤灰掺量和粗骨料对混凝土抗压强度的影响.

5 基于GS-SVR模型的交互式图形用户界面

目前，结构设计师和工程师更倾向于开发更强大和用户友好的软件以获得更广泛的适用性.为了确保本研究中开发的模型适用性和实用性，使用MATLAB编制了一个图形用户界面（GUI），如图10.整个界面分为两个主要部分，超参数的优化和已知输入参数的输出结果预测.GUI的操作可以通过点击帮助菜单获得，整个过程由4个主要步骤组成.

第1步：点击初始化设置按钮，获得参数的默认值，也可以手动修改.

第2步：点击优化按钮，获得参数C和g的最优值.

第3步：手动输入每个输入参数.

第4步：点击预测按钮，得到最终的输出值.

最后，通过点击预测按钮，直接显示粉煤灰混凝土的抗压强度.这个GUI主要是针对文中使用的数据集开发的，未来可以考虑对用户界面进行优化，如增加新的数据集和其他影响参数，使模型预测更加准确.

6 结论

文中采用混合机器学习模型GS-SVR来预测掺有粉煤灰的混凝土抗压强度，该混合模型将组成粉煤灰混凝土的六种成分和龄期作为输入变量，抗压强度作为输出变量，从相关文献中检索到的98个数据集上进行训练和测试，并对随机环境下的抗压强度的敏感性进行了定量分析.结果表明：

（1） 相比于原始SVR模型，改进后的SVR模型能够更准确地把握输入变量与输出变量之间复杂的非线性关系，在训练和测试阶段，GS-SVR模型的的相关系数R均超过98%，4个预测误差指标更小，抗压强度预测值与实验值的匹配度更好、预测精度更高，预测性能优于原SVR模型.

（2） 在随机环境下，随着变量随机性的增加，抗压强度的分布范围变宽，离散性变大；在7个变量中，混凝土抗压强度对粉煤灰最为敏感，其次是粗集料，对其他5个输入变量的敏感性较弱，设计人员应重点关注粉煤灰和粗集料的随机变化对混凝土强度不确定性的影响.

（3） 本研究提供了一个新的GUI，能够更加方便地预测粉煤灰混凝土的抗压强度，且表现出较为可靠的预测结果.

参考文献（References）

［1］ 胡毅，张陆山，袁福银，等.基于随机森林的混凝土强度预测研究[J].施工技术，2020，49（17）：89-94.

[2] 龙旭，毛明晖，卢昶衡，等.基于人工神经网络的混凝土类材料SHPB动态压缩性能预测[J].南京航空航天大学学报，2021，53（5）：789-800.

[3] 余海玲，郑建岚.基于Python人工神经网络的再生混凝土碳化深度预测[J].混凝土，2020（9）：52-55.

[4] 尚莉. 基于人工神经网络技术的机制砂自密实混凝土配合比设计研究[D].深圳：深圳大学，2020.

[5] 李启明，喻泽成，余波，等.钢筋混凝土柱地震破坏模式判别的两阶段支持向量机方法[J].工程力学，2022，39（2）：148-158.

[6] 李铁军，胡毅，刘茜，等.基于随机森林的支持向量机混凝土抗渗性预测模型研究[J].水电能源科学，2021，39（2）：119-122，118.

[7] 吴贤国，刘茜，王洪涛，等.基于随机森林和支持向量机的高性能混凝土抗渗性预测研究[J].硅酸盐通报，2021，40（3）：829-835，844.

[8] 王俊红，杨赛，刘富成，等.基于随机森林算法的混凝土早期抗裂性预测研究[J].信阳师范学院学报（自然科学版），2021，34（1）：158-165.

[9] 吴贤国，刘鹏程，陈虹宇，等.基于随机森林的高性能混凝土抗压强度预测[J].混凝土，2022（1）：17-20，24.

[10] 焦楚杰，谭思琪，崔力仕，等.基于神经网络的植生型多孔混凝土抗压强度预测模型[J].混凝土，2022（1）：7-10，16.

[11] 赵明亮，水中和，周华新，等.中低强度等级混凝土抗压强度的BP神经网络模型预测研究[J].混凝土，2021（3）：35-38.

[12] 张研，邝贺伟，曾建斌.再生保温混凝土抗压强度预测的相关向量机模型[J].混凝土，2020（9）：10-14.

[13] SOWJANY G V，ANADINNI S B，MAHADEVAIAH T. Application and validation of internally cured concrete strength characteristics by machine learning [J].Materials Today， 2023，24：68-79.

[14] JAGADESH P， PRADO-GIL J D， SILVA-MONTEIRO N， et al. Assessing the compressive strength of self-compacting concrete with recycled aggregates from mix ratio using machine learning approach[J]. Journal of Materials Research and Technology，2023，24：1483-1489.

[15] EL-MIR A， EL-ZAHAB S， SBARTA Z M，et al. Machine learning prediction of concrete compressive strength using rebound hammer test[J].Journal of Building Engineering，2023，64：231-245.

[16] AL-SHAMIRI A K， KIM J H， YUAN T F，et al.Modeling the compressive strength of high-strength concrete： An extreme learning approach[J]. Construction and Building Materials，2019，208：204-219.

[17] 吴佳，陈森朋，陈修云，等.基于强化学习的模型选择和超参数优化[J].电子科技大学学报，2020，49（2）：255-261.

[18] 沈錦鴻. 應用類神經網路配合ACI規範輔助卜作嵐混凝土配比設計[D]. 台湾： 国立交通大学， 2013.

[19] 马高，刘康.基于BP神经网络CFRP约束混凝土抗压强度预测[J].湖南大学学报（自然科学版），2021，48（9）：88-97.

[20] 陈庆，马瑞，蒋正武，等.基于GA-BP神经网络的UHPC抗压强度预测与配合比设计[J].建筑材料学报，2020，23（1）：176-183，191.