构造法在高中数学解题中的应用

摘要：构造法作为高中解题教学极其重要的思想方法，可以将抽象的数学知识直观化、具体化.应用构造法不但可以提升解题的速度与正确率，还可以透过问题本身把握数学知识的本质.本文中基于数学高考题的解题困境，通过借助构造法应用的解题思路探究，给出一些见解.

关键词：构造法；高中数学；应用

《普通高中数学课程标准（2017年版2020年修订）》中规定：“通过高中阶段的学习，使学生获得进一步学习及未来发展所需的四基知识、四基技能，引导学生会用数学眼光看待世界，用数学思维思考世界，用数学言语表达世界.”［1］新课标旨在将培养学生数学解题能力作为目标，构造法是常用的解题方法，在函数、几何与代数、概率与统计等教学板块中

的题目都可能会涉及到构造法的运用，用好构造法可以提升解题能力.

1 构造法基本内涵

所谓构造法就是在解决数学题目时，打破常规思维，结合题目给定信息，从新的视角出发，挖掘相关信息，简化解题过程，降低问题难度.在高中数学解题教学中，当常规思维对问题的解决造成困扰时，教师可以引导学生利用构造法解题，通过搭建相关信息的“桥梁”，构造新的数学对象，使问题得到顺利解决.构造法的解题步骤：首先，审题，找出题目的研究问题.其次，寻找与研究问题密切相关的概念.再次，将相关概念与研究问题相融合，探索该知识点的适用形式.从次，结合适用形式与相关知识点，构造新的解题思路.最后，将问题解决.

构造法的解题步骤：首先是分析题目，找出题目中所涉及的问题是什么.其次，带着题目中的疑问寻找与其密切相关的数学概念以及定理，去除无关变量，抓住中心点.然后，应用相关概念，找到构造这个知识点所必备的桥梁.通过所构造的形式融合相关知识点，对问题进行细致探究，最后使问题得以解决.

2 构造法在高中数学解题教学中的应用

构造法在高中数学中的地位是无可取代的，同时也是近年来高考数学必考的一种方法.许多数学问题的解决都需要借助构造各种形式的桥梁来完成，由此来看，有些问题的解决依赖构造法的使用，而构造法依赖构造思路的萌生.简言之，构造法的本质在于构造思路.如何更高效地利用数学构造法？这是本文需要探究的部分，下面结合高考数学中构造法的具体教学实例，并依据新课标规定的板块，从几个方面对数学构造法进行重点阐述.

2.1 函数构造法

函数可以说是贯穿整个数学教学，任何数学知识都可以与函数相结合.通过构造函数的方法解决未知问题，可以将复杂变量问题转化为简单变量，化繁为简.许多数学问题虽然表面上与函数并无直接关联，但通过深层次分析题目中的信息，可以构造与问题相关的函数，进而将数学问题转化为函数问题.函数构造法作为解题的辅助工具，通过运用函数的各种性质，解决数学问题［2］.

例1 （2023年新课标Ⅰ卷数学）已知在△ABC中，A+B=3C，2sin（A－C）=sin B.

（1）求sin A；

（2）设AB=5，求AB边上的高.

分析：基于题目可以看到，这是一道三角函数综合题，题中有正弦函数等量关系式，以及角度与边长的关系式，对此很多学生毫无头绪，但是通过审题发现可以借助两角和与差的三角函数公式、正弦函数定义进行解答.教师在讲授这类问题时，可以带领学生先审题分析题目的等量关系，引导学生自主书写解答过程，使其逐渐领悟题目的本质，在利用函数构造法解题时掌握解决问题的策略，使其融会贯通.

对于第（1）问，我们首先可以将题干中的条件A+B=3C进行转化，通过构造平角的形式得到了A+B+C=4C，由三角形内角和为π，得4C=π，于是得到角C为π4，代入原式整理得B=3π4－A，通过两角和与差的公式得2sinA－π4=sin3π4－A，进而整理得cos A=13sin A.根据三角函数平方关系式sin2A+cos2A=1，结合三角形三个内角的正弦值为正值，最终得到sin A的值为31010.

对于第（2）问，首先可以设AB边上的高为h，将已知条件借助正弦函数公式进行扩展，再借助三角形面积公式建立等量关系，最后化简整理便可得出.根据题干以及第（1）问的解答，利用正弦定理可得asin A=csin C.因为AB的长度为5，所以求得a为35.根据sin B=sin（A+C），得sin B的值为255.最后利用三角形的面积公式得12acsin B=12ch，求得AB边上的高为6.

从上述解答过程可以感受到构造法思想使问题由复杂变为直观，由繁变为简，有助于解三角形综合问题.因此，在教学过程中不应直接向学生展示问题的解决方案，而应激发学生的思维，帮助学生理解其中所包含的数学思想，以便能够举一反三、触类旁通.

2.2 几何构造法

立体几何知识始终是我们学习数学时的一个难点，这部分知识的学习对学生空间想象能力的要求比较高.因此，在学习时既要熟练掌握相关理论知识，又要注重培养立体感［3］.

例2 （2019年全国卷Ⅰ数学）如图1，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别BC，BB1，A1D的中点.

（1）证明：MN∥平面C1DE；

（2）求点C到平面C1DE的距离.

分析：这是一道典型的几何解答题，根据已知条件，可以通过对题干中的长度与角度分析构造某些等长关系以及多边形，从而有效解决已知条件与初始变量之间的关系，促进学生直观想象素养的提高.

对于第（1）问，要证线面平行可先证线线平行，关键是找到解决问题的钥匙，在这里笔者找到MN这条边，如果能够找到MN与三角形C1DE的一边平行，此问题即可得证.于是连接ME，B1C，根据中位线定理，得ME∥B1C，ME=12B1C.又由于ABCD-A1B1C1D1是直棱柱，且底边为菱形，因此A1B1∥DC，A1B1=DC，由此推出四边形A1B1CD是平行四边形，根据平行四边形的性质，得A1D∥B1C，A1D=B1C.因为N是A1D的中点，所以ND∥B1C，ND=12B1C.又因为ME∥B1C，ME=12B1C，得ND∥ME，MN=DE，推出四边形NDEM是平行四边，证出MN∥DE.又DE平面C1DE，所以得证MN∥平面C1DE.

对于第（2）问，观察这个直棱柱不难发现三棱锥C-C1DE的体积与三棱锥C1-CDE的体积相同.如果借助这个条件，设点C到平面C1DE的距离设为h，利用体积相等便能求出h.由于A1A=4，AB=2，因此C1C=4，CE=1，CD=2.在Rt△C1CD中，C1D=25；在Rt△C1CE中，C1E=17.根据C1D=2，CE=1这两个条件，得DE=3，所以△C1DE是直角三角形，则利用三棱锥C-C1DE体积公式，最终得到h=41717.

由上述这道几何高考题，可以深刻感受到抽象的数学知识可以形象地转为直观的数学问题，使问题变得更加立体，借助构造“辅助线”“直角三角形”这些特殊的例证，可以使问题与条件之间搭建起一座“桥梁”.

2.3 代数构造法

方程作为代数板块的重要内容，利用构造方程的思想来解决反映方程基本性质的问题，解决问题的步骤是将数学问题转化为方程问题，根据等量关系，建立数学模型，问题即可得以解决.

例3 （2023年新课标Ⅰ卷数学）设椭圆C1：x2a2+y2=1（a＞1），C2：x24+y2=1的离心率为e1，e2，若e2=3e1，求a的值.

分析：这是一道椭圆方程的求值题，在讲解时，可以带领学生分析题目中关于离心率的关系式，通过求出已知离心率，逐步得到未知离心率，达到求出a值的目的，促进学生数学推理能力素养的提高.

由于椭圆C2的方程是题目已给定的，因此可以得到C2的离心率e2的值为32.又e2=3e1，则e1为12，所以对于椭圆C1可得a2－1a2=14，解之得到a的值为233.

代数在高中数学中扮演着重要的角色，在算术运算、公式推导、方程求解、函数研究等活动中，不仅可以通过对现实生活中的变量关系和变化规律的探索，促进学生的探索和发现，而且可以培养学生的创新精神和实践技能.

2.4 概率与统计构造法

高中数学无论必修还是选修均涵盖概率的内容.同时概率常常与排列组合融合在一起，数学味比较浓、技巧性也非常强，解题时有些学生可能会被弄得晕头转向［4］.

例4 （2022年全国甲卷数学）甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局.三个项目比赛结束后，总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立.

（1）求甲学校获得冠军的概率；

（2）用X表示乙学校的总得分，求X的分布列与期望.

分析：这是一道概率与统计的综合题，根据题干，分开计算甲、乙两学校得分，通过采用分情况构造的方法，将复杂问题分解成几个简单问题求解，促进学生数据分析、数学抽象素养的提高.

对于第（1）问，由于比赛有三场，如想甲学校获得冠军，则甲学校至少需要获得两场胜利，共分为四种情况.情况一，甲学校三场比赛全部获胜，此时甲学校获得胜概率为P=0.16.情况二，甲学校获得第1，2场的胜利，此时甲学校获胜概率为P=0.04.情况三，甲获得第1，3场的胜利，此时甲学校获胜概率为P=0.24.情况四，甲获得第2，3场的胜利，则此时甲获得胜概率：P=0.16.将以上四种情况的概率相加即可得出甲获得冠军的概率为P=0.6.

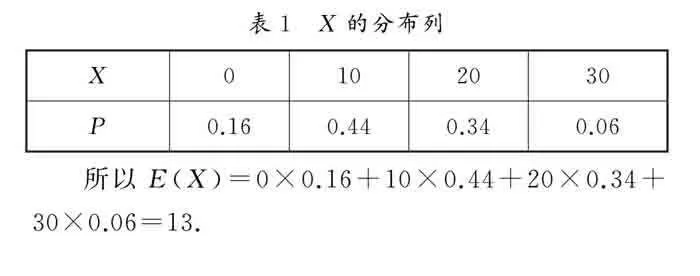
对于第（2）问，根据甲获胜的概率，可以推出乙在三个项目中获胜的概率分别为0.5，0.6，0.2.乙学校的总得分总共有四种情况，分别是0分、10分、20分、30分.乙获得0分说明三场比赛都输了，此时乙获得0分的概率为P=0.16.乙获得10分说明乙只赢了一场，此时总共有三种情况，分别是只赢第一场、只赢第二场、只赢第三场，此时乙获得10分的概率为P=0.44.乙获得20分说明乙获得了两场比赛，分别是获得第1，2场的胜利，获得第2，3场的胜利，获得第1，3场的胜利这三种情况，由上述概率情况可得出乙获得20分的概率为P=0.34.乙获得30分说明乙三场比赛都获胜，此时乙的获得30分的概率为P=0.06.

于是X的分布列如表1所示：

3 构造法的培养目标

构造法主要是在训练学生的数学逻辑思维、创新能力和思维敏捷性的基础上，引导学生利用实际问题的特点拓展思路.构造法通过对数学知识的创新，运用函数、几何学、概率等科学方法加以构建，使实际问题可视化，从而实现难题的化解.

3.1 加强数学严谨性的培养

数学题处处严谨、对称，充满数学之美，这些美的特征也需要构造，它体现在解题教学中，解题时需要从已知的数据和公式进行推导，对于高中学生数学思维严谨性的培养亦有很大效果.因此，为了加强学生的严谨性，需要提高学生的推理能力，通过逐步推演，从“怎样运算”到“为什么这样运算”，引导学生对数学算理有清晰的认识，使其严谨性得到提高.

3.2 提高构造法的应用意识

在数学教学过程中，教师要不断地将数学构造法渗透给学生，实现已有知识与构造知识的联结，使其达到知识的内化，并通过对高中数学题目的不断训练，极大地促进学生应用意识的提升.

测验对了解学生的知识掌握情况十分重要，实践是检验真理的唯一标准.因此，进行小节测验与章节测验是十分有必要的，教师根据教学计划与课程标准测试学生的学习成果，这样能随时了解学生的学习情况.测试不仅可以帮助学生形成自己的数学知识体系，还可以帮助学生培养良好的做题习惯.因此，教学中应该增加对数学构造法的检验.

3.3 加强构造法的方法探索

俗话说要敢于打破常规、敢于变革创新，要与时俱进.对于数学教学我们也该如此，不断探索适合中学数学构造法的教学方法，坚持“以人为本”，根据学生现有基础，寻找适合学生身心发展的方法，开阔学生的思维，深化学生对构造法的认识.

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020.

［2］李娟.构造法在高中数学解题中的应用［J］.中学生数理化（教与学），2017（8）：81.

［3］徐福安.高中数学立体几何的解题技巧和方法［J］.数理化解题研究，2023（12）：47-49.

［4］汤涛.现代社会离不开统计与概率［J］.科学世界，2020（1）：2.

Z