基于SOLO分类理论的2024年新高考Ⅰ卷第11题分析及教学改进

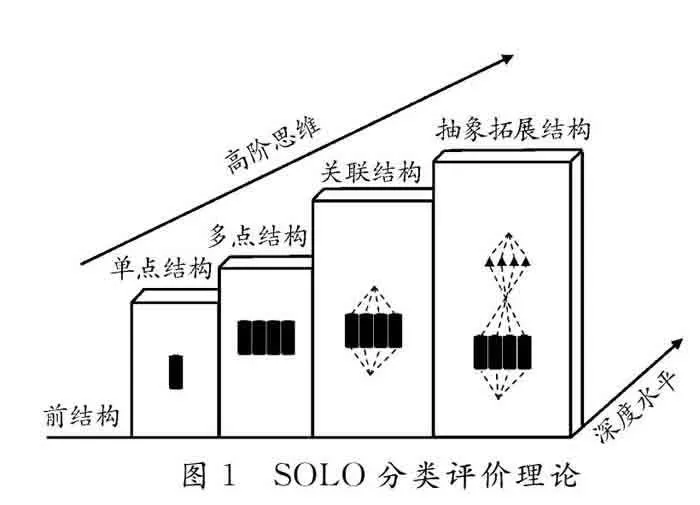
1 SOLO分类理论

SOLO分类法理论的含义是“可观察的学习结果结构”（Structure of the Observed Learning Outcome），其英文缩写为“SOLO”.该理论认为：我们难以对学生的认知水平和认知结构进行直接观察，但我们可以通过学生在回答某一问题时所表现出来的思维结构进行检测和分析，从而判断学生达到的思维层次.该理论将思维层次划分成五个水平，每个思维层次特征差异明显，各个思维层次的基本特征见表1.将该理论应用到试题分析中，可以对试题考查的思维层次进行划分，探究思维层次的考查梯度和侧重点，明确试题对于学生的思维层次的考查要求.SOLO分类理论明确了各思维层级的特征和要求，为学生思维水平的训练提供了重要参考.

SOLO分类评价理论如图1所示：

应用于高考数学试题分析中，SOLO分类理论具有以下四个显著优势.

1.1 系统性评估学生理解水平

SOLO分类理论提供了一个从简单到复杂的五个层次（前结构、单点结构、多点结构、关联结构和抽象扩展结构），这使得教师可以系统性地评估学生对数学概念的理解程度.这种系统性评估帮助教师有针对性地进行教学调整，提升学生的数学思维能力.

1.2 细致分析学生解题过程

SOLO分类理论强调对学生解题过程的细致分析，而不仅仅关注最终答案.通过分析学生在解题过程中展示出的理解和思考路径，教师可以发现学生在每个步骤中的优势和薄弱点.这种细致的过程分析能够帮助教师有针对性地辅导学生，提高他们的综合解题能力.

1.3 促进深度学习和迁移能力

SOLO分类理论的最高层次是抽象扩展结构，要求学生不仅能解决具体问题，还能将所学知识迁移到新情境中.高考数学试题中常常包含开放性问题和应用题，这就需要学生具备深度学习和知识迁移能力.通过SOLO分类理论的应用，教师可以帮助学生提升从基础知识到高级应用的能力，增强他们在面对陌生问题时的应对能力，从而提高整体数学素养.

1.4 指导试题设计与教学改进

SOLO分类理论不仅对学生的学习评价有帮助，还能指导教师设计更有效的数学试题和教学活动.通过分析高考数学试题中不同层次的题目分布，教师可以了解哪些层次的考查较为薄弱，从而在日常教学中有意识地加强相关内容的训练.同时，SOLO分类理论还可以帮助教师设计多层次的教学活动，确保学生在不同学习阶段都能得到适宜的挑战和支持，从而促进数学能力的全面发展.

2 真题呈现及解析

2.1 真题呈现

笔者选择2024年新高考Ⅰ卷第11题作为分析对象，主要基于SOLO分类理论的以下几方面原因：首先，该题作为选择题的压轴题，难度较大，具有多层次的思维要求，能够全面测试学生的认知水平.根据SOLO分类理论，该题不仅要求学生掌握基本的数学概念和技能，还需要进行复杂的关系理解和综合应用，符合该理论中多结构和延伸抽象的高阶认知水平.此外，题目的设计常常涉及多个知识点的综合应用，要求学生在解题过程中展示多层次的思维深度和广度，这恰好与SOLO分类理论的高阶认知要求相契合.因此，选择此题进行分析，可以深入探讨高考数学对学生认知能力的全面评估.

真题 造型 可以做成美丽的丝带，将其看作图2中曲线C的一部分.已知C过坐标原点O，且C上的点满足横坐标大于－2，到点F（2，0）的距离与到定直线x=a（a<0）的距离之积为4，则（ ）.

A.a=－2

B.点（22，0）在C上

C.C在第一象限的点的纵坐标的最大值为1

D.当点（x0，y0）在C上时，y0≤4x0+2

2.2 试题解析

设曲线C上的动点为P（x，y），则x>－2且（x－2）2+y2×|x－a|=4，因为曲线过坐标原点，则（0－2）2+02×|0－a|=4，得a=－2，故选项A正确.

曲线方程为（x－2）2+y2×|x+2|=4，而x>－2，所以（x－2）2+y2×（x+2）=4.当x=22，y=0时，（22－2）2×（22+2）=8－4=4，则（22，0）在曲线上，故选项B正确.

由曲线的方程可得y2=16（x+2）2－（x－2）2，取x=32，则y2=6449－14，而6449－14－1=6449－54=256－24549×4>0，此时y2>1，故C在第一象限内点的纵坐标的最大值大于1，故选项C错误.

当点（x0，y0）在曲线上时，由上面分析得y20=16（x0+2）2－（x0－2）2≤16（x0+2）2，则－4x0+2≤y0≤4x0+2，故选项D正确.

3 试题分析

3.1 试题的结构水平分析

该试题主要考查学生的多点结构水平和关联结构水平.在多点结构水平上，学生需要理解并应用多个知识点；在关联结构水平上，题目要求学生将这些知识点有机结合，综合分析曲线的特点，特别是在不同象限中的特征以及点与曲线的关系等.选择题的各个选项实际上考验了学生对知识点之间相互关系的深刻理解，以及将这些关系与图形结合的能力.通过这种多点关联的考查，试题旨在评估学生的综合分析能力和逻辑推理能力.

3.2 结构水平考查的特征

在多点结构水平和关联结构水平的考查中，学生不仅需要掌握单个知识点，还必须能够将不同的知识点结合在一起，形成完整的解决方案.试题中涉及的距离关系要求学生理解距离的几何意义，并将其应用于曲线的方程和点的坐标关系中.同时，选项中的各个判断条件，如点的纵坐标的最大值、函数关系式等，也要求学生通过对曲线的深入分析，判断这些条件是否满足.因此，这类试题不仅要求学生具有良好的数学基础，还必须具备较强的综合能力和灵活应用的能力.

3.3 结论与意义

该试题不仅考查学生对单个数学概念的掌握程度，更强调了学生在面对复杂问题时的综合分析能力和逻辑推理能力.这样的题目可以有效区分出不同层次的学生，特别是那些在知识整合与应用方面表现突出的学生.这进一步说明了多点结构和关联结构水平在高考数学题中的重要性，学生只有在这些层面上取得突破，才能在考试中脱颖而出.

4 教学改进建议

4.1 强化多点结构水平的教学，通过综合练习提高学生的知识整合能力

2024年新高考Ⅰ卷第11题考查了学生在多点结构水平上的能力，要求学生能够整合多种知识点来解决问题.因此，在教学中，应注重培养学生的综合分析能力，通过设置包含多个知识点的综合练习题来提升学生的思维深度.

4.2 培养关联结构水平的能力，通过实际应用和情境设置深化学生的逻辑推理

为了帮助学生更好地理解和运用关联结构水平中知识点的关联，教师应注重将数学概念与实际问题相结合.在教学中，教师应注重引导学生从多个知识点的关联中发现问题的核心逻辑，并通过逻辑推理得出结论.通过模拟高考压轴题的设置，教师可以帮助学生理解如何在复杂问题中抓住关键，并运用关联结构水平的思维模式，逐步提高他们的逻辑推理和综合分析能力.这不仅有助于应对高考中的复杂问题，也能为学生的长期数学学习打下坚实基础.