老教师与年轻教师的一节课

【摘要】文章以“平面直角坐标系”一课为例，通过观摩本校老教师邹老师的课堂教学，并与自己入职第一年的课堂教学进行对比，从复习引入、新课教学、知识运用、课堂小结四个方面进行分析，谈谈自己的体会和对教学的启示。

【关键词】初中数学；对比教学；平面直角坐标系

当今快速发展的社会对人才的要求更高，作为培养新时代少年的年轻教师，更要与时俱进并践行终生学习的理念。

一、教学过程的对比与分析

1.复习引入环节的教学对比

（1）邹老师的课堂教学片断。

师：我们前面学习了数轴，数轴包含三要素，分别是什么？生：原点、方向、单位长度。

师：我们为什么要学习数轴，它给我们研究数学带来什么好处呢？（一系列问题串）生A：数轴上的点可以表示数，且与实数一一对应。生B：利用数轴可以方便比较数的大小。生C：数轴还可以确定两点间的距离和数的绝对值。生D：数轴还可以表示不等式、不等式组的解集。

师：非常好，那么生活中我们是如何确定物体位置的呢？比如棋子，电影院的座位。一个数还够吗？生E：必须两个。

师：什么给你的启示？生E：电影票。

师：五排六列和六列五排是一个位置吗？生E：不是。

师：也就是说这数对是有顺序的，那么给你一个平面，如何确定一个点的位置呢？生F：两个数轴。

师：两个数轴就会有两个原点，两个正方向，两个单位长度，那么该怎么画呢？生F：两个数轴要互相垂直，同一个原点，同一个单位长度。

师板书，画一个直角坐标系。

（2）笔者的课堂教学片断。

笔者：同学们我们前面已经学习了数轴，什么是数轴？生：规定了原点、方向、单位长度的直线。

笔者：很好，我们还知道数轴上的点和实数是一一对应的，那么平面上的点该如何表示呢？请大家思考生活中的事例，队列中的战士、电影院的座位、教室里的学生。我们都是通过排和列来描述的，也就是说要有两个数，并且这两个数是有顺序的。两排三列和三排两列是不一样的。我们也可以借助这种“有序数对”来表示平面内的点。这就是今天我们要学习的平面直角坐标系。

（3）对比分析。邹老师通过三个主要问题，不仅复习了旧识，引出了新知，更重要的意义在于沟通了新旧知识之间的内在联系，并为本节课的教学构建了一个好的框架。学生可以用同样的模式研究坐标系，即以类似的三个问题进行思考。而笔者的教学过程并没有对数轴进行深入的复习，仅仅是表面上的复习，显然对学习本课帮助不大。并且笔者在课堂上以讲为主，没有充分发挥学生的主观能动性。

2.新课教学部分的对比

（1）邹老师的课堂教学片断。

师：点P除了用数对（4，3）表示外，还可以有其他数对来表示它吗？（停顿、引导）生：没有，因为过一点有且只有一条直线与已知直线垂直。

师：很好，那反过来，数对（4，3）除了表示点P外，是否还会表示其他的点？生：不会，两条直线相交有且只有一个交点。

师：非常好，对于平面内的任意一点P可以确定唯一一个有序实数对（a，b），反过来有序数对（a，b）也可以唯一确定一点。也就是说平面内的点与有序实数对一一对应的，我们将有序实数对称为点的坐标。确定点的坐标同学们要注意，先垂线，后垂足，找出有序实数对，先横后纵再括号，中间隔开用逗号。

（2）笔者的课堂教学片断。

笔者：一般地，对于坐标平面内的任意一点P，过点P作x轴的垂线，垂足为M，可得点M在x轴上所对应的实数a；再过点P作y轴的垂线，垂足为N，可得点N在y轴上所对应的实数b，那么有序实数对（a，b）表示点P，因为过一点作已知直线的垂线能且只能作一条，所以这样的有序实数对是唯一确定的……

（3）对比分析。对于知识点“平面内的任一点都有唯一的有序实数对与之一一对应”的归纳，邹老师放手让学生思考回答，在课堂上就有一位学生给出了非常完美的答案。而笔者的课堂只是按照板书讲解，并没有给学生思考的时间和表达的机会。

3.新知运用部分的教学对比

（1）邹老师的教学设计。

课堂教学片段：

师：点E的坐标是？生：-4。

（有质疑声）

师：好像有不同意见，你再好好想一想我们是如何确定点的坐标的？把机会留给你，再试一试吧。生：（-4，0）。

师：你是怎么做的？生：先向Pyem6orQAsgWRew9YjeDCqSY95CjOIjFQm6qaA3rNFU=x轴作垂线，对应-4。再向y轴作垂线对应0。

师：嗯，非常好，经过自己的努力，把这问题解决了。

（2）笔者的课堂教学设计。

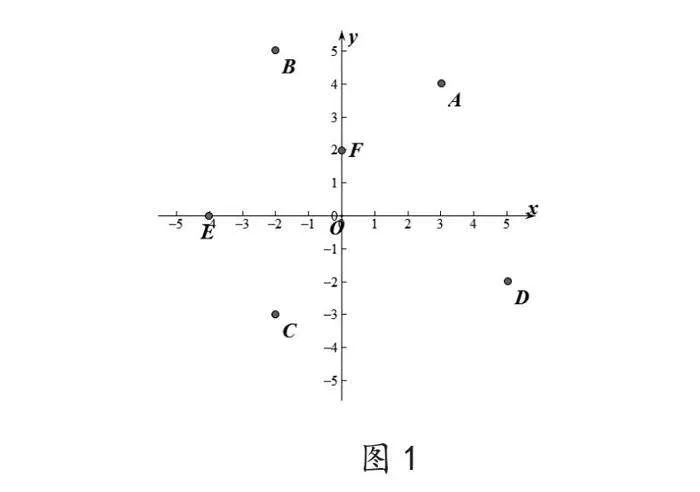
例1：写出图2中直角坐标平面内各点的坐标。

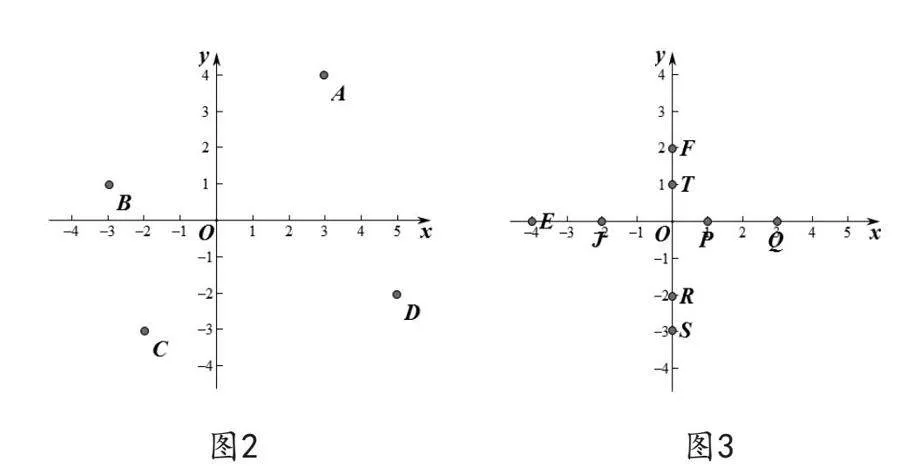
例题2：写出图3中坐标轴上各点的坐标。

（3）对比分析。例题的设计，邹老师巧妙地将课本中例1和例2合二为一，并将B点稍做改动。由特殊到一般，学生更容易理解接受。在对比的过程中，也加强了学生对点坐标的确定方法，理解坐标的有序性。笔者在例2中多设计了几个坐标轴上的点，学生更容易发现坐标轴上点坐标的特征。

4.课堂小结环节的教学对比

（1）邹老师的教学设计。

三个问题：学什么？怎么做？为什么学？并提供故事和寄语。

（2）笔者的教学设计。

平面直角坐标系：①坐标轴：横轴（x轴），纵轴（y轴），坐标原点。②直角坐标平面内的点与有序实数对建立一一对应关系。③点的坐标，点的坐标表示方法，P（a，b）。④x轴上点的坐标是（x，0）；y轴上点的坐标是（0，y）；坐标原点的坐标是（0，0）。

（3）对比分析。邹老师的小结给笔者耳目一新的感觉，学生以三个问题为依据进行小结归纳，并且小结又分三个层次。而笔者仅仅停留在本节课的知识层面，没有体现知识之间的联系和发展。

二、思考和启示

1.复习引入——关注新旧知识之间的联系

通过复习引入符合学生的认知规律。通过复习，建构起新旧知识之间的桥梁。学生在复习回顾的过程中，能够进一步掌握旧知识或者解决问题的方法，为学习探究新的知识做好准备。

2.新课教学——关注知识的生成过程

日常教学要以知识的生成、发生、发展为主线，重视基本数学概念的抽象，数学公式、解题方法的概括总结、归纳推导过程，把课堂还给学生，做到以学生为主体。

3.新知运用——关注练习设计的多样化和层次性

数学课堂中练习是不可或缺的。围绕教学目标，侧重教学重难点，设计多样化、有层次的题目。形式多样化，独立完成，小组合作完成。有时也可以采取游戏的方式，这既可巩固知识，又能提高学生的学习兴趣。

4.课堂小结——关注知识的系统性

课堂小结不能仅仅局限在一节课的知识层面，更重要的是注重知识间的联系。通过小结，搭建知识框架，建立知识体系，为学生的后续发展打下坚实的基础。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.