借“图”分析分层建模

【摘要】数形结合是一种有效的数学思考方式，可以帮助学生更直观地理解和解决问题，也能够帮助学生建立不同的解题模型，适应不同难度的题目，提高数学思维能力。因此，在教学中，应该注重数形结合思想的渗透和应用，让学生在解决问题的过程中感受到数学的乐趣和魅力。

【关键词】数射线；四舍五入；建模；数形结合；推理

“数射线”是学生学习“数”时经常出现的一个工具，借助数射线，可以将抽象的“数”直观形象化。借助数射线，学生能够直观地判断出某数最接近的整万数、整十万数等，那么，借助数射线的表征，是否也能将这道题目隐性的思考过程外显？

一、数形结合在教学中的实践

要想引导学生化数为形，借助数射线推测出最接近30000的数的范围，首先学生需要熟悉“借数射线学四舍五入的过程”。

1.借“图”引入，初现模型

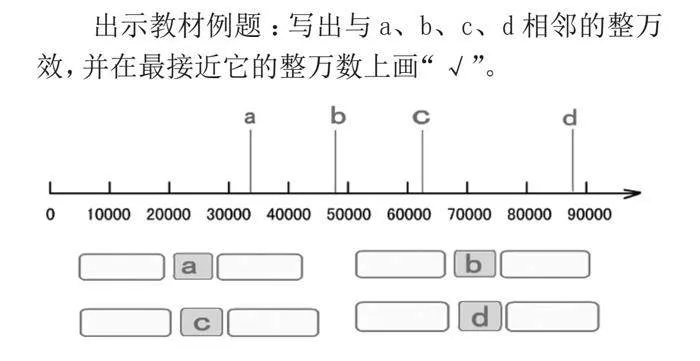
出示教材例题：写出与a、b、c、d相邻的整万效，并在最接近它的整万数上画“√”。

师：a可能是哪个数？为什么？（32995、35641、37864）

生：我认为a可能是32995。因为a接近30000，这三个数中只有32995更接近30000。

师：在30000和40000之间除了点a（32995）接近30000，还有哪些数？

生：我觉得应该是30000和35000之间的数都是接近30000的！

师：怎么想到一定到35000呢？

生：35000是30000和40000的中间数。比这个中间数小的数是接近30000的。

教学意图：借助数射线，通过不断地追问，直观感知以中间数为界，小于中间数的数接近前一个整万数，大于中间数的数接近后一个整万数。为后续发现“找最接近的整万数看千位与5的大小关系”这一现象做铺垫，也为后续自主探究找最接近整十万数、整千万数等方法做准备。而这一切又是为下一节课归纳总结“四舍五入法”做引入铺垫。为了拓展学生的思维，这节课上提出了一个课后思考题，目的是为引导学生由局部观察到整体观察，为后续的问题探究做准备。

2.借“图”分析，再现模型

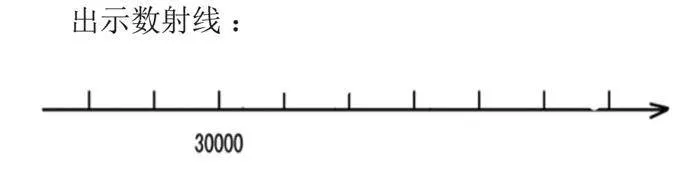
出示问题：有一个大数，四舍五入到万位是3 0000，这个数最大是（ ），最小是（ ）。

师：这个大数四舍五入到万位是30000，也就说明什么？

生：这个大数最接近的整万数是30000。

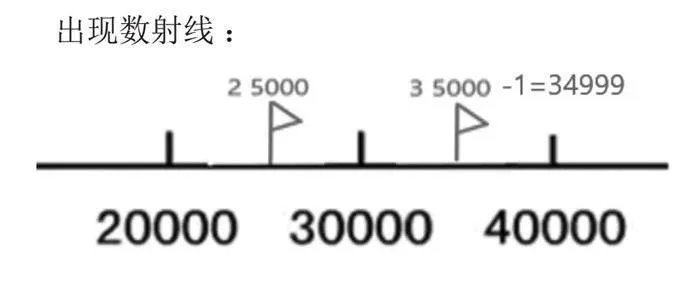
出示数射线：

师：在这条数射线上，哪些数是接近30000，你能说出大致范围吗？

生1：有很多，这些数大概在20000和40000之间。

师：为什么？

生1：30000相邻的整万数是20000和40000，所以应该在这个范围里找。

师：这个范围里的所有数都是吗？

生2：不是，范围再缩小点，应该是25000和35000之间的数。

师：25000和35000是怎么来的？说说你的想法。

生2：前几节课中，我们已经知道了以中间数为分界线，中间数前面的数是接近前一个数的，中间数后面的数是接近后一个数的。20000和30000的中间数是25000，30000和40000的中间数是35000，因此接近30000的数在25000和35000之间。

问：那么这个数最小是25000，最大是35000？

生3：按照四舍五入法，25000接近30000是对的，但是35000接近40000，不对。所以应该是35000前一个数，也就是35000-1=34999。

出现数射线：

生总结：先找到一个大致的范围，也就是30000相邻的两个整万数。再缩小范围，找到前后的两个中间数。然后确定了前一个中间数就是要找的最小数。后一个中间数减去1就是最大数。

3.借“图”推理，巩固模型

出示问题：一个大数，四舍五入到万位是30 0000，这个数最大是（ ），最小是（ ）。

一个大数，四舍五入到万位是300 0000，这个数最大是（ ），最小是（ ）。

学生画图，得到以下结论：

师：这三道题目，有什么共同点？

生：都是将一个大数四舍五入到万位，根据得到的近似数找最小数和最大数。

师：解决问题的方法是什么？

生：画数射线的方法。先找到这个近似数的相邻整万数，再找前后中间数。最后根据中间数确定最小数和最大数。

4.各取所需，分层建模

对于能力强的学生来说，在经历画图解决一系列问题后，会有一些发现，比如：（1）最小的数小于得到的近似数。最大的数大于得到的近似数。（2）如果四舍五入到万位，就把近似数减5000得到最小数，把近似数加5000再减1得到最大数；如果四舍五入到十万位，就把近似数减50000得到最小数，把近似数加50000再减1得到最大数，以此类推。（3）找准尾数，尾数之前的数减去1，尾数改写成5和相应个数的0，就是最小的数；尾数之前的数保留，尾数改写成4和相应个数的9就是最大数。

根据这些发现，部分学生就可以比较快捷地推出最小数和最大数，简化解题的过程。而对于一些能力较弱的学生，借“图”也能逐渐推理出最小数和最大数，最终，学生根据自己的认知水平，选择合适的解题方法，在这个过程中，学生的思维能力得到了不同水平的发展。

二、数形结合在教学中的反思

1.数形结合，直观化的探究过程，让建模更有效

数射线的引入，化抽象为直观，让学生在解决最大数问题时深入理解“近似数可以比原数小，也可以比原数大”其次，附近的数也有远近之分，借助数射线，学生又能直观地从图中提取到这样一个信息“中间数是辨别远近的一个标准”。在数射线的直观支持下，学生通过一些合情合理地推导，找到了一些显而易见的结论，最终解决了问题。数形结合，让抽象的数学与直观的图形结合起来，让抽象的思维直观化，帮助学生打开思维大门，突破了数学理解的难点。而数形结合的运用，也实现了学生按自己的能力水平建立不同解题模型的需求。

2.数形结合，一以贯之，让建模更顺畅

如果在“四舍五入”的新授课中，没有借助“数射线”展示四舍五入概念的形成过程，那么，没有这个经验基础，学生很难和这种方法产生亲近感，在整个借“图”建模的过程中，依然会困难重重。因此，让“数形结合”这一思想一以贯之，是学生有效建模的基础。新授课上，借助数射线，引导学生直观感知“中间数与数的大小关系”对“判断最接近数”的作用，进而洞察到隐含其中的“四舍五入”的规律，从而理解四舍五入的产生过程，这个知识形成的过程是非常重要的，将对学生知识的迁移整个过程，非常自然而连贯，利于学生感受到“数形结合”的思考方式带来的乐趣，从而激发学生形成应用这个思想方法去解决问题的欲望。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2002.

[2]王永春.小学数学与数学思想方法[M].上海：华东师范大学出版社，2022.