建立模型驱动教学，深化规律迁移应用

【摘要】新课程理念下的数学教学要结合具体内容，重视问题情境的创设，使学生经历数学知识形成与应用的过程，教学中要采取“问题情境—建立模型—解释—应用与扩展”的模式，引导学生在经历知识的形成与应用的过程中，进一步理解、掌握数学知识。

【关键词】建立模型；自主学习；迁移应用；学以致用

数学源于生活，所以课堂教学中应该联系实际，注重对数学事实的体验，让学生在生活中、实践中学习数学，从而体验学习数学的价值与意义。现以沪教版教材二年级上册《数学广场—幻方》为例，具体谈谈在课堂教学中如何采用“问题情境—建立模型—解释—应用与扩展”的模式，激发学生学习兴趣，在观察、讨论、猜想、验证中建立学习过程。

一、创设故事情境，童趣化引入模型

笔者以教材为引擎，从激发学习兴趣、渗透探究方法、培养探索习惯三个维度，设计单元整体教学。主要设计思路如下：笔者先让学生由龟背上的图案，化抽象为具体，用数来表示点图引出正方形数表，寻找数表中的规律，再通过位置变换判断幻方，由此来引出3个幻和是15的幻方，探究其数的特征，并通过设计填幻和为15的幻方加深规律的应用，最后通过变幻方将知识点进行迁移应用，提升学生的推理能力和判断能力。

1.龟背洛书，激发兴趣

在实际的教学活动中，教师应该充分挖掘小学数学教学内容中的实用性，从生活的角度加强对学生的引导和启发。通过结合语文阅读篇目《大禹治水》引入洛书。

（1）引入洛书。古时候有一位治水英雄，你们知道是谁吗？大禹治水还有一个数学故事呢，很久以前，有一个这样的传说……

（2）出示视频。当时天下洪水泛滥，大禹奉命治水。由于不了解水情，治水屡次失败，一度陷入困境。一天，一只五彩神龟从河中走出。大禹根据神龟的指点，最终治水成功。

（3）龟背洛书。这只神龟神奇在哪？传说神龟背上的纹理排列成奇妙的图案，被后人称为洛书。这节课我们一起来研究龟背上的图案，探寻其中的奥秘。

低年级的孩子当看到熟悉的动画形象时学生瞬间兴趣高涨，蕴含新知的故事立刻激发了学生的思考，教师适时提问，“这只神龟神奇在哪？”同学们各抒己见，从而激发对幻方的进一步探究。

2.观察猜想，认识幻方

让学生用数学的眼光观察龟背上的图案，用小圆点表示数，引出正方形数表。再由观察正方形数表到猜想各行各列、对角线上3数之间的关系，通过计算加以验证，对幻方建立初步认识。教学片段如下：

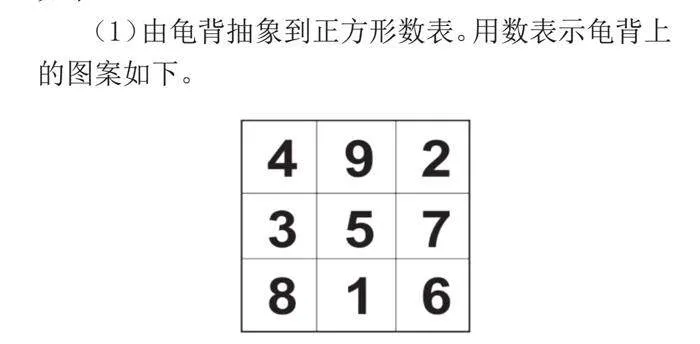
（1）由龟背抽象到正方形数表。用数表示龟背上的图案如下。

（2）从不同角度观察正方形数表。观察表格发现：横着看有3行，竖着看有3列，斜着看有两条对角线。

提问：这些3个数之间有着怎么的关系？有什么共同点？

猜想：3个数的和是一样的。（打开书本算一算）

（3）寻找数表中的规律。教师让学生交流反馈，并验证猜想。

发现：每一行的3个数、每一列的3个数以及对角线的3个数之和都是15。

小结：具有这样神奇特点的正方形数表，我们叫它幻方。幻方的和我们叫“幻和”。这是一个幻和为15的幻方。

通过童趣化的问题情境让学生快速进入学习状态，充分调动学生观察的积极性，从一个正方形数表中抽象观察到每行、每列、每条对角线上数的特点，猜想每行每列每条对角线上的3数之和都相等，再进行计算验证，初步感悟到什么是幻方，对幻方的数学模型建立初步认识。

二、利用游戏活动，趣味化理解模型

教师在教学中要善于创设趣味化、模型化的问题情境，来吸引学生的注意力。例如笔者在本节课新授的第二个教学环节中，为充分调动学生的探究欲，初步认识完幻方的特征后，通过交换幻方中数的位置，小朋友们自然而然地就会主动思考“正方形数表发生了变化后，还是幻方吗？”，带着这样的问题学生很快进入新知的探究学习中去。变换位置，判断幻方的教学片段如下：

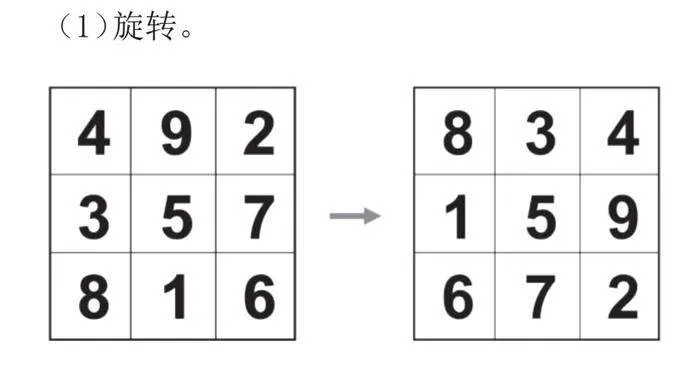
（1）旋转。

提问：幻方发生了怎样的变化？有什么办法证明它是幻方？

验证：每行、每列、每条对角线上的3数之和都是15。

小结：原来中间数不变，剩下8个数旋转一下，幻和还是15。

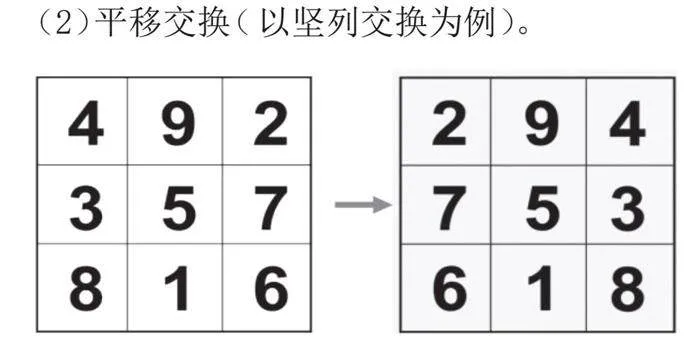
（2）平移交换（以坚列交换为例）。

小结：判断是不是幻方时，只要算出和有不相等的情况时就不用再往下算了，这样的方法又快又好。当9个数每行、每列、每条对角线的和都相等的时候才是幻方。

通过旋转、平移让模型趣味化，引导学生学会对比观察，加深幻方模型的建立，轻松地理解、运用幻方的特征判断幻方的思路和方法。

三、巧设悬念问题，思维化构建模型

小学生对新鲜事物的兴趣很强烈，只要在课堂合理运用教材中的新知识、新方法并及时激疑，使小学生由疑生趣，以疑诱思，由疑获知。比如在本节课的第三个教学环节中，根据第二个环节中由1～9组成的三个幻方引出问题，“1-9组成的幻方除了9个数不一样之外，幻方里的数字排列也非常特别，他们还有什么特征？”问题一提出课堂上顿时活跃起来，大家各抒己见。此时教师再让学生通过小组合作讨论自主探究进而开展实验、推理活动，将学生的思维得到锻炼和提升。

创设情境促进了学生思考，能够提出有价值的数学问题，挖掘幻方模型里蕴藏的规律，这不仅让每个学生都处于求知的迫切之中，同时为随后的教学提供了初步的感知，使得学生进一步理解幻方模型。

四、动手实验操作，活动化应用模型

1.激活旧知，学以致用

在本节课的练习巩固环节中，笔者创设学生实践操作的问题情境：还有一只龟背上也有一些数，每行、每列、每条对角线上3个数的和都15。可时间久了，很多数都看不清了。让我们一起来帮他们把丢失的数找回来吧！

整个填数的过程都让学生自己利用数卡实践操作，使他们经历尝试、计算、应用、检验的全过程，这样学生贴近自己生活的问题情境中动手实践解决问题、获得知识和经验，同时深刻体会到计算并检验的广泛应用。

2.以点到面，深化思考

教学中可通过提问“如果这9个数都减少了1，现在这个正方形数表还是幻方吗？”让学生在原本幻方模型的基础上，调用已掌握判断幻方的方法，来验证自己的猜想，每个数都减少了1，那么每行、每列、每条对角线上的和比原来减少了3，即幻和是12，还是幻方。

教师应该以学生发展为本，在数学课堂中应加强教学策略优化改进，充分发挥有效的问题情境，调动学生课堂学习参与积极性，提升学生思维，实现素质能力全方面提升，为今后学习发展奠定坚实基础。

【参考文献】

[1]冯小根.谈如何在小学数学课堂中创设有效问题情境[J].中学生作文指导，2020.

[2]刘建安，张安元，侯芳兰.电子书包环境下小学数学[J].数学教学研究，2022（02）.