以学促练，感悟小数的本质

［摘 要］以苏教版数学教材三年级下册“小数的初步认识”的教学为例，通过教材解读确定学习目标，设计了以下的教学活动：寻找小数，帮助学生体会小数就在身边；认读小数，帮助学生掌握小数的读写法；结合情境，帮助学生理解小数的含义；追溯历史，帮助学生了解小数的应用。这样以学促练，使学生经历了探索小数奥秘的过程，真正感悟小数的本质，有效培养了学生的逻辑推理能力和数学思维。

［关键词］苏教版教材；小数；以学促练

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）21-0016-03

《义务教育数学课程标准（2022年版）》中强调，课程资源开发与利用要坚持育人为本，将促进学生身心健康发展作为首要任务，不仅要满足教与学的多样化需求，还要注重资源开发精品化。因此，教师要根据具体的教学内容和学生的实际情况，精心设计教学流程和巩固练习，并在实践过程中不断优化和改进，以突破教学重难点，提升学生的数学核心素养。

下面，以苏教版数学教材三年级下册“小数的初步认识”的教学为例进行说明。这是学生第一次学习小数的知识，也是数概念的再一次扩充。在这之前，学生学习了“分数的初步认识”，为五年级学习“小数的意义和性质”“小数加法和减法”做准备。“小数的初步认识”这节课的教学重点是初步理解小数部分是一位小数的含义，这是因为比较小数的大小、进行小数加减法计算都是在初步理解小数含义的基础上进行的，也是今后进一步学习小数意义和性质的基础；教学难点也是初步理解小数部分是一位小数的含义，这是因为小数的意义比较抽象。结合具体情境初步理解小数部分是一位小数的具体含义，学生不仅需要正确理解十分之一的含义，还要根据生活经验综合感知和逐步理解。

基于教学目标和重难点设计教学活动与练习，确定本节课的教学目标为：（1）结合具体情境理解一位小数的含义，能正确读、写小数部分是一位数的小数；（2）能用小数表示日常生活中的简单数量，进一步发展数感和初步的推理能力，体会数学思考的合理性，提高解决问题的能力；（3）能在初步认识小数的过程中，进一步体会小数与生活的密切联系，体验小数的作用和价值。

【课堂回顾】

一、寻找小数，体会小数就在身边

师：大家看课题，今天我们学习什么？（认识小数）你在生活中哪些地方见到过小数？

生1：我在体温计上见到过小数。有一次测量体温，体温计上显示我的温度是37.4℃。

生2：我在游乐园买票的时候见到过小数——身高低于1.2米的儿童不用买票。

生3：我在考试卷上见到过小数，因为有一次我考了99.5分。

生4：我在超市买东西的时候见到过小数，如一支笔的价格是2.5元……

师：看来，小数在我们生活中有着非常广泛的应用。这节课，我们就来研究小数。

……

二、认读小数，掌握小数的读写法

师：同学们，你们能在黑板上写出几个小数来吗？（学生写出以下小数：0.27，1.3，13.87，1.29，99.50）你能读出这些小数吗？

生1：0.27读作零点二十七……

生2：不对。0.27应该读作零点二七，因为小数点后面的数只要依次读出来就可以了。如1.3读作一点三，13.87读作一三点八七……

生3：不对。13.87应该读作十三点八七，因为小数点前面的数应按照整数的读法。如1.29读作一点二九，99.50读作九十九点五零。

师：我们一起来读一读这些小数。（师生共读小数）中间的小数点把一个小数分成了整数部分和小数部分，谁能总结一下小数的读法？

生4：小数点前面的数按照整数的读法，小数点后面的数只要依次读出来就可以了。

师：你能找到这五个小数中的整数部分和小数部分吗？

生5：0.27的整数部分是0，小数部分是27；1.3的整数部分是1，小数部分是3；13.87的整数部分是13，小数部分是87；1.29的整数部分是1，小数部分是29；99.50的整数部分是99，小数部分是50。

……

三、结合情境，理解小数的含义

1.理解人民币模型中一位小数的含义

出示题目：我买了一支铅笔0.8元，需要付多少钱？

师：同学们，你们能读出这个小数吗？

生1：0.8读作零点八。

师：0.8元是多少钱呢？

生2：0.8元是8角，因为0是整数部分，表示0元；8是小数部分，表示8角。

师：那是因为我们把1元分成了10个1角，1个1角就是0.1元。那1角用分数怎么表示？8角用分数又怎么表示？

生3：1角用分数表示是[1/10]元，8角用分数表示是[8/10]元。

师：也就是说，0.8元=8角=[8/10]元。你能照着这样子，说一说0.1元、0.5元吗？

生4：0.1元=1角=[1/10]元，0.5元=5角=[5/10]元。

……

2.学后练习巩固，掌握人民币的小数模型

师：同学们，我们来练一练。（出示下题，见图1）请你先在括号里填上小数，再读一读这些小数。

生5：一个菠萝包的价格是8角，用小数表示是0.8元，读作零点八元；一个小麻花的价格是9角，用小数表示是0.9元，读作零点九元；一包饼干的价格是1元3角，用小数表示是1.3元，读作一点三元；一盒牛奶的价格是2元4角，用小数表示是2.4元，读作二点四元。

师：我们再来看第二题（见图2），请你用合适的小数表示这些人民币的币值。

生6：左边有1个1元和2个1角的硬币，所以用小数表示是1.2元；右边有1张5元、1张2角和1张1角的纸币，所以用小数表示是5.3元。

师：（出示□.□□元）同学们，学到这里，我们来总结一下这里的三个方框分别表示什么意思。

生7：小数点前面的是整数部分，表示元；小数点后面的第一位数表示角，小数点后面的第二位数表示分。

……

3.理解长度模型中一位小数的含义

出示信息：桌面长5分米，宽4分米；小红身高1米3分米。

师：你们知道5分米是几分之几米？4分米呢？1米3分米呢？

生8：5分米是0.5米，因为把1米平均分成10份，每份就是1分米，5分米就是其中的5份；4分米是0.4米，因为把1米平均分成10份，4分米就是其中的4份；1米3分米是1.03米……

生9：不对。1米3分米是1.3米，因为3分米表示0.3米，与1米合起来是1.3米。

师：我们把1米平均分成10份，每份是1分米，用小数表示是0.1米，用分数表示是[1/10]米。现在我们知道了5分米等于0.5米，那你能用分数来表示0.5米吗？0.4米呢？

生10：5分米=0.5米=[5/10]米，4分米=0.4米=[4/10]米。

师：还有1米3分米=1.3米。刚才有同学说1.03米表示什么呢？

生11：1.03米表示1米3厘米。

师：谁来报一报自己的身高，并说一说表示身高的这个小数表示什么意思？

生12：我的身高是1.54米，表示1米5分米4厘米。

生13：我的身高是1.39米，表示1米3分米9厘米。

师：（出示2.2米）谁来读一读这个小数？你知道这是谁的身高吗？

生14：2.2米读作二点二米，这是姚明的身高。

师：（出示□.□□米）同学们，学到这里，我们来总结一下这里的三个方框分别表示什么意思。

生15：小数点前面的是整数部分，表示米；小数点后面的第一位数表示分米，小数点后面的第二位数表示厘米。

4.学后练习巩固

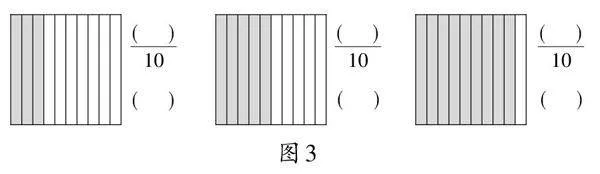
师：同学们，下面我们来练一练。（出示图3）请看图先写出分数，再写出小数。

生16：第一幅图是把一个长方形平均分成10份，取其中的3份，用分数表示是[3/10]，用小数表示是0.3；第二幅图是把一个长方形平均分成10份，取其中的5份，用分数表示是[5/10]，用小数表示是0.5；第三幅图是把一个长方形平均分成10份，取其中的9份，用分数表示是[9/10]，用小数表示是0.9。

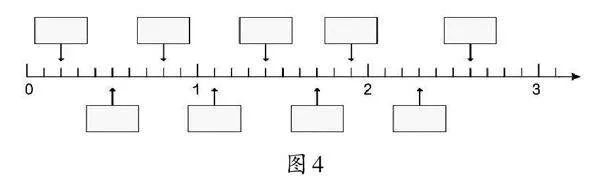
师：我们再来看第二题（见图4），请在方框里填上小数。

生17：先看0～1这一段，把1平均分成10份，每份是0.1，所以2份就是0.2，5份就是0.5，8份就是0.8；再看1～2这一段，1再多1小格就是1.1，1再多4小格就是1.4，1再多7小格就是1.7，1再多9小格就是1.9……

……

四、追溯历史，了解小数的应用

师：这节课，我们认识了小数，那你们知道小数是怎么产生的吗？让我们一起来看一段有关小数产生的小视频。（观看视频）谁来说一说自己知道了有关小数的哪些历史？

生1：我国古代是用小棒来表示数的，为了表示小数，就把小数点后面的数放低一格。最早使用小圆点作为小数点的是德国数学家克拉维斯，还有一部分国家是用逗号表示小数点……

师：（出示华罗庚名言）著名数学家华罗庚说过：“宇宙之大，粒子之微，火箭之速，地球之变，生物之谜，日用之繁……无处没有数学的重要贡献。”虽然这节数学课接近尾声了，但是我们研究小数的路还将继续……

【课后思考】

“小数的初步认识”是培养学生数感的重要内容，它既是学生对十进制数字系统深入理解的关键，也是后续学习小数大小比较、小数加减法等知识的基础。

首先，在教学内容的设计上，注重从生活实际出发，引导学生发现并感知小数的存在和价值。在课堂导入环节，教师通过提问“你在生活中哪些地方见到过小数？”，让学生真切地体会到小数在实际生活中的广泛应用，从而激发他们探究小数意义的兴趣。同时，教师还通过对比整数与小数的异同，使学生明白小数是对部分单位的精确量化，是十进制数字系统中的一部分，能够更加细腻地描述数量关系。

其次，在概念建构环节，遵循学生的认知规律，引导学生由浅入深，循序渐进理解概念。教师从分数入手，借助人民币模型和长度模型的演示，帮助学生建立小数与分数的内在联系，理解小数的位值概念。同时，教师强调小数点的作用以及小数数位的含义，确保学生掌握小数的读写规则。

最后，重视以学促练，学练结合。教师鼓励学生学习新知后，立即完成2～3道练习题。这样不仅能检测学生的学习效果，还能促进学生自主归纳总结课堂所学，感受到数学的魅力。

本课教学，在学与练的轻松愉快氛围中，教师不仅引导学生经历了探索小数奥秘的过程，使学生习得新知，还通过多样化的练习，让学生体会到数学之美，培养了学生的逻辑推理能力和数学思维，实现了提升学生核心素养的目标。

［ 参 考 文 献 ］

[1] 杨潇.追求数学本质 实施深度学习：以苏教版三年级下册“小数的初步认识”教学为例[J].数学学习与研究，2022（31）：92-94.

[2] 吴旭娇.探究本质：生长式概念教学的务本诉求：以苏教版数学三年级下册“小数的初步认识”教学为例[J].小学教学研究，2020（12）：80-82.

[3] 杨潇.追求数学本质 实施深度学习：以苏教版三年级下册“小数的初步认识”教学为例[J].数学学习与研究，2022（31）：92-94.

（责编 杜 华）