HPM视角下“等差数列前n项和公式”的教学

［摘 要］ 因为数列是特殊的函数，所以利用函数思想来解决数列问题很重要. 数列在整个高中数学中占有重要地位，是高中数学的核心知识. 文章在HPM视角下对“等差数列前n项和公式”进行研究，带领学生在相应数学史的理解下更好地运用相关知识去解决问题.

［关键词］ HPM视角；数列；高中数学教学

《普通高中数学课程标准（2017年版2020年修订）》中的高中数学课程目标提到，在学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养［1］. 纵观高中数学课程新结构，数学文化贯穿始终，成为培养学生数学学科核心素养的有效载体［2］. 数学史作为数学文化不可或缺的一部分，承载着培育和发展学生数学学科核心素养的使命，蕴含着丰富的数学教育价值［3］. HPM视角下的数学教学基本方法就是重构历史、追求知识自然发生的教学法，即以学生的认知起点出发，凸显所学知识的必要性，呈现知识的自然发生过程，激发学生的学习动机. 如果一个数学概念、一种思想方法从天而降，那么我们直接相信它必然是不符合历史的. HPM视角下的等差数列教学可以帮助学生建立完整的知识体系. 数列源于生活，如人口增长率、分期付款、储蓄等实际问题，利用数学建模的思想将现实生活与数学知识紧密结合，引导学生理解数学源于生活且应用于生活；数学知识与数学史相融合，可以扩宽学生的数学视野，使学生了解不同国家的数学文化.

历史素材的选取

1. 高斯算法

据说，200多年前，高斯的算术老师提出了这样一个问题：1+2+3+…+100=？

当其他同学忙于把100个数逐项相加时，10岁的高斯却用下面的方法迅速算出了正确答案：（1+100）+（2+99）+（3+98）+…+（50+51）=101×50=5050.

高斯的算法解决了等差数列1，2，3，…，100的求和问题，但是将其推广到解决一般等差数列1，2，3，…，n，…的求和问题时，会发现需要讨论项数n的奇偶性.

2. 毕达哥拉斯的三角形数

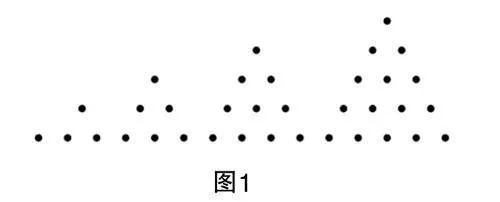
毕达哥拉斯学派在世界数学史上首次建立了数和形之间的联系，研究过问题1+2+3+…+n=？的几何表示.早期毕达哥拉斯学派似乎已经熟悉利用小石子或点来构造三角形数、正方形数和长方形数等［4］. 本文中，笔者主要研究三角形数（如图1所示）.

3. 《九章算术》之“良马和驽马”

今有良马与驽马发长安至齐，齐去长安三千里，良马初日行一百九十三里，日增一十三里；驽马初日行九十七里，日减半里. 良马先至齐，复还迎驽马. 问：几何日相逢及各行几何？［5］

13世纪中国数学家杨辉在解决《九章算术》中的“良马和驽马”问题时，通过构造几何图形来求良马（第一天行193里，以后每天增加13里）和驽马（第一天行97里，以后每天减少半里）在十五天内走过的路程.用今天的数学语言来表达良马的行走情形就是：求首项为a（a>0），公差为d（d>0）的等差数列的前n项和，可构造长分别为a，a+d，a+2d，…，a+（n-1）d，宽均为1的n个长方形，则所得的“阶梯形”的面积之和就是所求的等差数列的前n项和［6］.

4. 《张丘建算经》的第23、22题

（1）今有女子不善织，日减功迟.初日织五尺，末日织一尺，今三十日织讫.问织几何？

（2）今有女善织，日益功疾. 初日织五尺，今一月日织九匹三丈. 问日益几何？

教学过程的设计

1. 引入历史，发现公式

师：200多年前，高斯的算术老师提出一个问题：1+2+3+…+100=？高斯如何求解？

生1：（如图2所示）将1与100配对，将2与99配对，以此类推，共有50组，并且他们的和都是101，结果就是101×50=5050.

师：大家想过为什么要一头一尾两两配对吗？

生2：因为一头一尾两两配对，原本100个不同的数，就变成了50个相同的数.

师：通过这样的处理，把一般问题转化成特殊问题，也就是把不同数的求和问题转化成相同数的求和问题. 高斯是德国数学家，近代数学的奠基者之一，拥有“数学王子”之称. 他在天文学、测量学、磁学、光学等领域有杰出贡献. 现代的尺规作图也得益于高斯的贡献.

设计意图 “高斯问题”在曾经的学习中提到过，其是一个以1为首项，1为公差的等差数列求和问题，由于学生的认知基础、认知潜能、认知风格等存在差异，此处回顾让学生清楚“高斯问题”的缘由，以及为本节课教学“等差数列的前n项和”做铺垫，从而很好地发展学生的逻辑推理、数学运算等核心素养.

师：如图3所示，你能用算式表示这个几何图形吗？

生3：在右上角加上一个同样的图形，将其倒放就可以拼成一个长方形. 和就是长方形的长乘宽再取其一半，也就是长方形面积的一半，即=5050.

师：长方形的长和宽分别代表什么数？

生4：宽100代表100组数，长101代表一组数的和为101，100×101为100组数的和，除以2就得到50组数的和，即1+2+3+…+100的和.

设计意图 先从“数”的方面分析“高斯问题”的缘由，再从“形”的角度进行分析，引导学生深入理解. 由“数”能够准确地想到“形”，由“形”能够联系到“数”，有助于提升学生的数形结合能力和几何直观能力，以及数学抽象和逻辑推理等素养，增强学生运用几何直观思考问题的意识，帮助学生在具体情境中感悟事物的本质，为后面的倒序相加法的学习做铺垫.

师：推广到n项（如图5所示），你能计算1+2+3+…+n的和吗？

生5：1+2+3+…+n=. 类比1+2+3+…+100的和的计算，如图6所示，在长方形中，一共有n组数，一组数的和为n+1，n（n+1）为n组数的和，除以2就是1+2+3+…+n的和，所以1+2+3+…+n=.

师：看来同学们迁移知识的能力很不错. 其实，毕达哥拉斯学派在世界数学史上首次建立了数和形之间的联系. 早期毕达哥拉斯学派似乎熟悉利用小石子或点来构造三角形数、正方形数和长方形数等. 今天我们一起来看一下三角形数. 从1开始，任意多个连续自然数之和构成三角形数，如图7所示. 毕达哥拉斯学派当时提出的就是在三角形数旁补上一个倒立的三角形数，如图8所示.

师：我国古代数学家对数列的认识也很早，如《九章算术》《周髀算经》《孙子算经》《张丘建算经》《前汉书》《旧唐书》等著作，都载有许多有趣味的数列问题.

设计意图 将“特殊”推广到“一般”，将“已知”推广到“未知”，带领学生灵活运用并真正理解高斯的算法，培养学生的逻辑思维能力；使用毕达哥拉斯学派的三角形数，通过数形结合，使得数学问题更加形象化.

2. 逻辑演练，公式证明

师：已知等差数列｛a｝的首项为a，公差为d，你可以求它的前n项和S吗？

生6：S=a+a+…+a+a.

师：毕达哥拉斯学派通过构造图形来计算，我们可用数学语言将其表达出来.

S=a+a+…+a+a①.

构造另一个与其相同的等差数列将其“倒置”.

S=a+a+…+a+a② .

将①式和②式相加，得到

2S=[][n对]=n（a+a）③.

所以等差数列｛a｝的前n项和公式为S=④.

师：若一个数列｛a｝中，与首、末项等距的两项之和等于首、末两项之和，可把正序的和式与倒序的和式相加，得到一个常数列的和，这一求和方法称为倒序相加法［7］. 倒序相加法的本质就是分组配对，转化成相同数的和来处理.

前面学过等差数列的通项公式为a=a+n（n-1）d，如果用此公式替换④式中的a，将得到什么样的结果呢？

生7：S==，化简得S=na+. 所以等差数列｛an｝的前n项和公式为

设计意图 通过引入高斯定理，以及毕达哥拉斯学派的三角形数，使学生对等差数列的前n项和的由来有一定认识. 通过使用数学语言来表达本节课所学习的知识，让学生在情境中抽象出数学概念，积累从具体到抽象的活动经验，从而提高学生的数学抽象、逻辑推理、数学运算等核心素养.

3. 公式应用，加深理解

例1 根据下列各题中的条件，求相应的等差数列｛a｝的前n项和S.

（1）a=-4，a=-18，n=18;

（2）a=14.5，d=0.7，a=32.

设计意图 使用课本上的练习题，引导学生更加理解等差数列的前n项和公式，为接下来解决“良马和驽马”问题做铺垫，从而发展学生迁移知识的能力.

例2 《九章算术》的盈不足章节中有这样一题：今有良马与驽马发长安至齐，齐去长安三千里，良马初日行一百九十三里，日增一十三里；驽马初日行九十七里，日减半里. 良马先至齐，复还迎驽马. 问几何日相逢及各行几何？

教师将例2转化为等差数列的前n项和问题：

良马的：=；

驽马的：=.

当它们的和为6000时就得到我们想要的结果.

学生求解：+=6000，化简得12n2+567.5n=12000.

待学生计算后，教师给出答案：约等于15.69.

师：这是我们用数列求和的一般方法求解的，接下来一起看我国古代数学家杨辉在解决“良马和驽马”问题时使用的“盈不足术”：先假设两马在第十五日相逢，再通过构造几何图形来求良马和驽马在十五天内走过的路程. 我们将特殊情况推广到一般情况：在良马的情形中，用今天的数学语言来表达就是求首项为a（a>0），公差为d（d>0）的等差数列的前n项和，可构造长分别为a，a+d，a+2d，…，a+（n-1）d，宽均为1的n个长方形，则所得到的“阶梯形”的面积之和就是所求的等差数列的前n项和，如图9所示.

师：请同学们看一看，计算“阶梯形”的面积之和，直接相加小长方形的面积过于烦琐，那么怎样计算更简便呢？请同学们小组讨论.

第一小组：可以将它补充为一个梯形，求梯形的面积，再将多余的部分减掉. 如图10所示，多余的部分就是阴影部分. 梯形的上底为a，下底为a+（a+nd），高为n，则梯形的面积为n［a+（a+nd）］，再减掉多余的n个小三角形的面积之和，得到S=n［a+（a+nd）］-nd，最后化简得S=na+n（n-1）d.

第二小组：将其补成一个长方形，如图11所示，并将其分为两个部分来求和. 第一部分由n个面积为a的小长方形组成，其面积之和为na；第二部分是边长为（n-1）d和n的长方形，其面积为n（n-1）d. 因此，等差数列的前n项和为第一部分的面积与第二部分面积的一半的和，即S=na+n（n-1）d.

第三小组：本小组使用的是倒序相加法. 如图12所示，在“阶梯形”右边加上一个倒置的相同图形，拼成一个长为a+a，宽为n的长方形. 将这个长方形的面积算出来，取其一半，也就是我们所要求的等差数列的前n项和，得到S=na+n（n-1）d.

师：第一小组将“阶梯形”补成一个完整的梯形，第二小组和第三小组则都是将“阶梯形”补成一个完整的长方形，其中第三小组使用的是倒序相加法.用这三种方法最终都得到了等差数列的前n项和.

设计意图 使用“良马和驽马”问题让学生知道数学源于生活，数学方法可以用来解决实际问题. 利用“阶梯形”将枯燥、繁杂的文字直观地展示出来，能促进学生的数形结合思想发展；使用小组讨论的方式探究“阶梯形”，可增强学生的团队合作能力，让学生充分理解运算对象，掌握运算法则，获取运算思路，求得运算结果，提高学生的数学运算、逻辑推理等核心素养.

4. 布置作业，提升能力

【必做题】

题1：根据下列各题的条件，求相应等差数列｛a｝的有关未知数.

（1）a=20，a=54，S=999，求d及n；

（2）d=，n=37，S=629，求a及a；

（3）a=，d=-，S=-5，求n及a；

（4）d=2，n=15，a=-10，求a及S.

题2：请根据下列条件计算.

（1）今有女子不善织，日减功迟. 初日织五尺，末日织一尺，今三十日织讫. 问织几何？

（2）今有女善织，日益功疾. 初日织五尺，今一月日织九匹三丈. 问日益几何？

注释：“日减功迟”指每日减少的量相同. “讫”指结束.“织几何”指织了多少尺.

【选做题】

我们在课堂上用“阶梯形”求得了递增等差数列的求和公式，那么你会使用“阶梯形”求得递减等差数列的求和公式吗？

设计意图 必做题中求未知数的题目意在使学生更进一步地掌握等差数列的求和公式，发展学生的顺向思维和逆向思维；应用题借鉴历史中的数学问题，意在让学生知道数列在生活中的存在和使用，帮助学生理解等差数列前n项和公式的运用，从而培养学生的逻辑思维能力；选做题意在使学生尝试做属于自己的“阶梯形”，从而提高学生的数学建模等能力.

结语

数学史告诉我们，任何属性的概念、公式、定理、思想等都不是从天上掉下来的，都有其自然发生和发展的过程. 将数学史融入数学课堂，使学生对数学知识既能“知其然”，又能“知其所以然”；既能知其“今生”，又能知其“前世”；既能“近观树木”，又能“远眺森林”［8］. 本节课通过“高斯问题”引入课题，将特殊问题转化为一般问题，先使用图形表示等差数列的前n项和，再从代数的角度证明公式，进而培养学生的逻辑推理、数学抽象、数学运算和直观想象等数学核心素养. 在教学过程中融入数学史，如毕达哥拉斯学派的三角形数、杨辉的“盈不足术”等，构建“知识之谐”. 通过小组讨论，学生从中体会到数学知识的来源，营造“探究之乐”. 让学生感受数学源于生活，与公式“零距离”接触，使学生成为课堂真正的主人. 使用多种方法探究等差数列的前n项和公式，彰显“方法之美”， 给学生搭建一座贯穿古今数学文化的桥梁，感受数学文化带来的巨大吸引力，引发“情感之悦”. 数学史的有效渗透，展示数学家们探究数学孜孜不倦的精神，达成“德育之效”“能力之助”.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］. 北京：人民教育出版社，2020.

［2］ 余庆纯. HPM微课融入高中数学教学的行动研究［D］. 五邑大学，2018.

［3］ 洪燕君. HPM教学实践驱动下初中数学教师专业发展研究：MKT的视角［D］. 华东师范大学，2017.

［4］ 王蓉. 基于HPM理论的课堂教学实践与思考——以《等差数列的前n项和》教学为例［J］. 数学教学通讯，2016（33）：9-12.

［5］ 曹纯. 九章算术译注［M］. 上海：上海三联书店，2015.

［6］ 汪晓勤，陈君煜. HPM视角下数列教学中的直观想象素养初探［J］. 中小学数学（高中版），2019（04）：57-60.

［7］ 相阳. 例析倒序相加法的应用［J］. 语数外学习（高中版中旬），2020（12）：39.

［8］ 汪晓勤. 数学史与高中数学教学［M］. 上海：华东师范大学出版社，2020.