基于ACT-R理论的“高中数学探究活动”教学实践与思考

［摘 要］ 针对高中数学教材中数学探究活动的教学现状，结合ACT-R理论，以斐波那契数列教学设计为例，引导学生进行学习实践，并对ACT-R理论应用于高中数学探究活动教学实践进行反思.

［关键词］ ACT-R理论；数学探究活动；教学实践

问题提出

《普通高中数学课程标准（2017年版2020年修订）》（简称新课标）提到高中数学课程要注重促进学生实践能力和创新意识的发展. 已有研究表明数学探究教学可以增强学生的创新意识和实践能力，同时对增强学生数学学习自信心起着积极作用. 由于不作为考试内容、课时紧张、学习难度大等因素，新课标所规定的数学探究活动没有得到足够重视，大多数教师在组织教学时直接跳过这部分内容，更谈不上对其进行研究并开发新的学习项目，这显然不符合新课改的要求. 鉴于此，笔者尝试使用ACT-R理论对高中数学探究活动进行教学设计，收获颇多，在此提出分享.

ACT-R理论与高中数学探究活动

1. ACT-R理论概述

ACT-R理论的一个基本观点是：可以由相对简单的原理形成相对简单的知识单元，再由这些相对简单的知识单元构成复杂的认知［1］. 它的基本内涵是：任何知识的习得都是始于陈述性阶段，经过一段时间的程序化处理，最终过渡到自动化阶段［2］. ACT-R理论将知识分成两类：陈述性知识和程序性知识. 陈述性知识：用信息块来表征，可以用“是什么”来回答；程序性知识：通过提取陈述性信息块来达到目标的规则性单元，是回答“如何做”的知识.ACT-R理论由教学设计流程图和各环节设计的思维导图构成，为教师深度理解数学、深度理解学生和深度教学提供了强有力的技术支撑.

2. 数学探究活动

数学探究活动是指以解决具体问题为目的，要求学生观察分析数学事实，提出有意义的数学问题，猜测、探求适当的数学结论和规律，以及解决问题的思路和方案，并给出解释或证明［3］.

3. ACT-R理论与数学探究教学

数学探究活动教学的实施是为了使学生更好地理解数学本质，提升学生的数学思维水平. 不仅要合理设置探究问题，创设有探究意识的问题情境，还要注重数学探究活动组织形式、探究手段的设计，适时引导学生进行合作. ACT-R理论与数学学习结合在一起，倡导将复杂的数学问题简单化，比建构主义理论和情境认知理论更加注重知识的逻辑性，对学生认识数学学习本质有很大的帮助［4］. 不仅如此，还有助于学生更好地理解数学知识，解决学习中存在的困惑，达到一个更好的教学效果.

数学探究活动与ACT-R理论有密切的联系，即基于ACT-R理论，在数学探究活动教学中，将陈述性知识通过熟练操作转化为程序性知识，通过精致练习使程序性知识更加自动化，引导学生用数学思维分析各要素之间的关系，进而提升学生的应用和创新意识［5］.

基于ACT-R理论的斐波那契数列教学设计

斐波那契数列与黄金分割是人教A版（2019）选择性必修第二册教材第四章“数列”（第10～11页）中“阅读与思考”的内容. 斐波那契数列与等差、等比数列一样，都是从现实背景中抽象概括出来的重要数列模型，而数列又是特殊的函数，基本遵循函数的研究路径：背景—概念—性质—应用. 模型、数形结合、转化与化归、函数与方程、极限等都是探究数学问题时常用的思想方法，充分体现了数学探究活动的研究手段.

1. 学习内容及认知分析

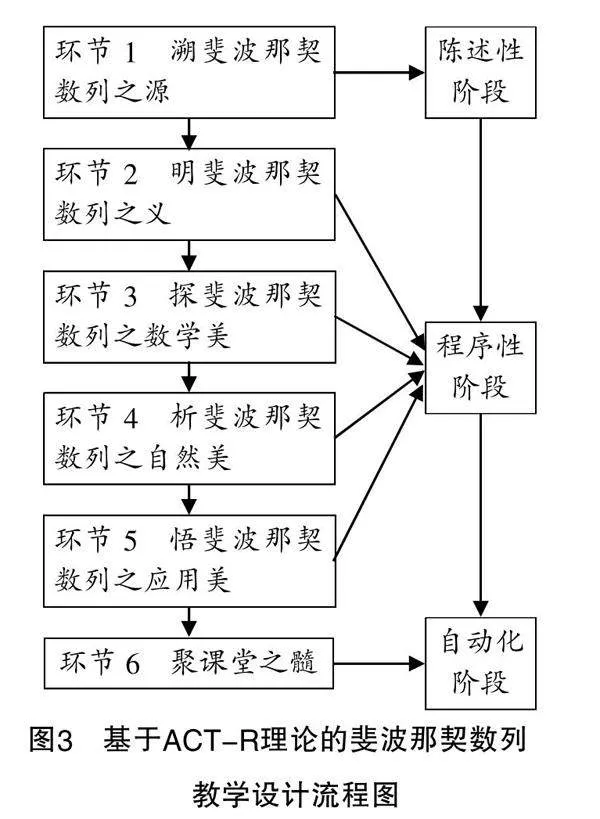
本节课主要的教学内容包括斐波那契数列的概念、递推公式、通项公式、性质、实际应用. 在此之前，学生学习了数列的概念，以及等差数列和等比数列的定义、通项公式、性质、前n项和公式和简单应用，这些都为本节课的学习奠定了知识基础. 基于ACT-R理论的本节课结构思维导图如图1所示.

2. 学习目标

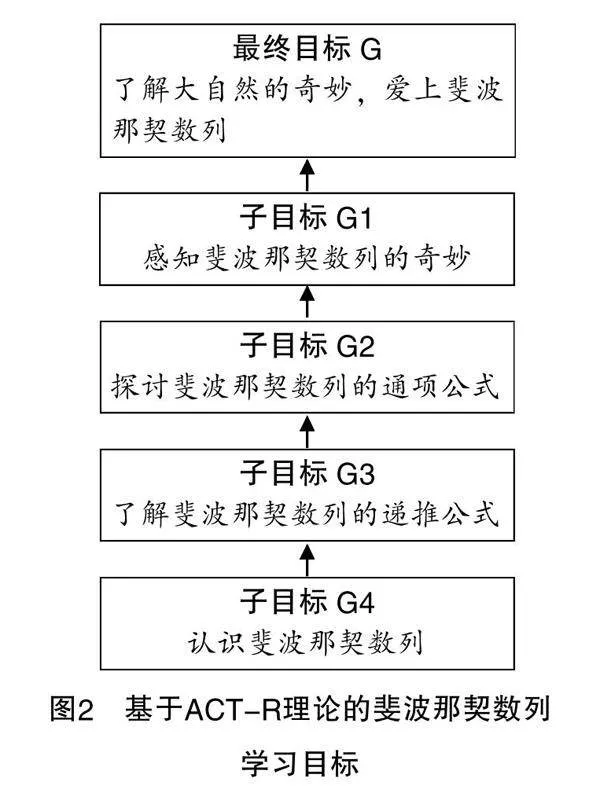
与等差数列和等比数列相比，斐波那契数列的取值规律及性质比较隐蔽且不易发掘. 另外，学生对数列问题的求解思路和方法的应用不够灵活，其应用意识、创新能力也不够强. 现依据ACT-R理论和实际学情对本节课的学习目标进行层级分解，并将其展示如下（如图2所示）：

学习目标

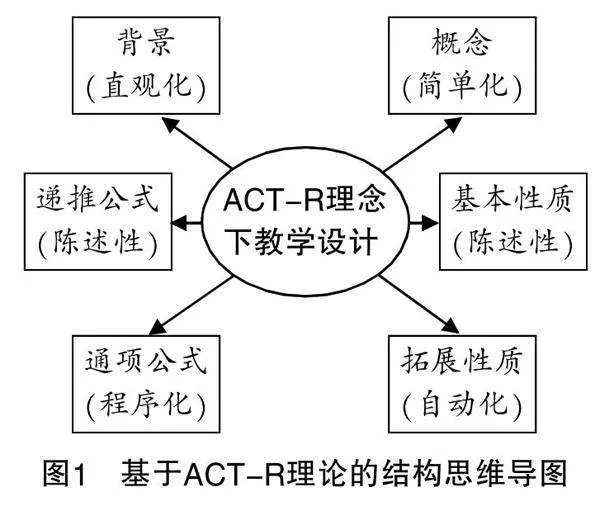
3. 基于ACT-R理论的斐波那契数列教学设计流程图

如图3所示.

4.基于ACT-R理论的斐波那契数列教学过程

环节1 溯斐波那契数列之源.

师：在前面几节课中，我们已经学习了等差数列、等比数列的基本知识，也熟悉了研究数列的一般路径，体会到了数列强大的魅力所在，还有哪些值得我们研究的数列呢？让我们先来看一段视频——《达·芬奇密码》.（播放视频）

师：视频中的密码重新排序后，它到底揭示了什么秘密？时间要回溯到1202年，一位叫列昂纳多·斐波那契的意大利数学家，他出版了一本书，叫《算盘全书》. 该书介绍了一个神秘的数列——斐波那契数列.

设计意图 在陈述性阶段获取陈述性知识：利用数学史引入课题，集中学生的注意力，激发学生的求知欲，起到良好的教学效果.

环节2 明斐波那契数列之义.

问题：如果1对兔子每月能生1对小兔子（一雄一雌），而每1对小兔子在它出生后的第3个月里，又能生1对小兔子，假定在不发生死亡的情况下，由1对初生的小兔子开始，1年后会有多少对兔子？

师生活动：教师解读题目要求，带领学生分析并填写到第3个月，学生自主完成后面9个月的填写.

学生活动：尝试用树状图、列表等方法得到第4至12个月的兔子对数.

追问1：你是怎么得到这些月份的兔子对数的？

追问2：这个规律适合每个月的兔子对数吗？

追问3：假设第n个月的兔子对数为F，你能用数学符号语言表达这个规律吗？

师生总结：按照这个规律，我们能得到更多月份的兔子对数，这些数构成了一个数列. 由于这个数列最早是由斐波那契提出的，为了纪念他，人们把这个数列称为斐波那契数列，通常记为｛F｝，数列中的项称为斐波那契数. 斐波那契数列的递推公式为

F

=F=1，

F

+F

=F（n≥3，n∈N*）.

设计意图 用ACT-R理论把大问题分解为一系列的子问题：通过问题串的设置，引导学生总结出斐波那契数列的递推性质，抽象出斐波那契数列模型.

环节3 探斐波那契数列之数学美.

师：除了前面总结出来的递推公式，斐波那契数列还有哪些性质呢？（提供通项公式的一个雏形）

活动1：类比等差、等比数列的研究内容及研究方法，对斐波那契数列展开探究.

预设1：学生探究斐波那契数列的通项公式；

预设2：学生探究斐波那契数列相邻两项的比值.

师生活动：教师组织学生合作探究，小组代表汇报探究成果.

①当斐波那契数列的项数越来越大时，相领两项的比值越来越接近黄金比

≈0.618

；②斐波那契数列的通项公式为F=×

-

.

设计意图 用ACT-R理论将复杂问题简单化，促使学生关注数学本质. 等差、等比数列的学习经验是本节课探究活动的生长点，在斐波那契数列的探究过程中，学生从已有的陈述性知识出发.

环节4 析斐波那契数列之自然美.

师：其实斐波那契数列不仅仅有数学美，它还有自然美、被称为大自然的密码. 现在我们一起来感受斐波那契数列的自然美.

活动2：动手操作，深化探究.

用所给的正方形纸片拼成矩形（从最小的两个正方形开始，每次添加一个正方形）. 如图4所示，阴影部分的矩形面积是多少？最外围的大矩形面积是多少？由此你可以猜想到什么结论？若从内到外依次连接通过小正方形的四分之一圆弧，能得到什么样的奇观？

师生活动：学生独立思考后，小组展开互学互助.

引导学生推广“用不同的方法计算每次所得矩形的面积”得到的等式，归纳出斐波那契数列的又一个性质：F+F+F+···+F=FnFn+1.

师：（PPT展示）从内到外依次连接通过小正方形的四分之一圆弧，能得到一条螺旋线，被称为斐波那契螺旋.

师：欣赏视频，向日葵的两组交错的螺旋结构、鹦鹉螺的螺旋结构等，动态感受自然界中动植物与斐波那契数列的联系，体验斐波那契数列的自然美.

设计意图 ACT-R理论把陈述性知识看成信息块，通过主动探索，从陈述性知识向程序性知识过渡，激活信息块，顺利提取产生式规则：从“形”的角度继续探究斐波那契数列与黄金分割之间的关系，以形助数，发现新性质；以数释形，用数学符号语言表达图形隐含的规律.

环节5 悟斐波那契数列之应用美.

例题 已知斐波那契数列1，1，2， 3，5，8，13，21，34，55，….

（1）a+a+a+…+a是斐波那契数列中的第_______项；

（2）1+a+a+a+…+a是斐波那契数列中的第_______项.

设计意图 ACT-R理论倡导“精致练习”，激活产生式规则和信息块：例题设置意在巩固斐波那契数列的性质和递推公式，让学生感悟数学是现实的、有用的.

环节6 聚课堂之髓.

师：本节课我们学习斐波那契数列经历了怎样的过程？请同学们完成相应的学习成果报告. （报告内容见表2）

设计意图 ACT-R理论认为，这正是在程序性目标和信息块的基础上形成的自动化阶段，即迁移数学能力，总结活动经验，总结研究方法，构建知识网络，培养数学交流和表达能力.

ACT-R理论对数学探究活动教学的启示

ACT-R理论倡导将复杂的数学问题简单化，强调精致练习，提倡重视两类知识的获得和迁移等，为数学探究活动提供了丰富的、可借鉴的教育理论，为数学探究教学设计提供了强有力的支撑，也是落实数学探究活动的一种重要途径.

1. 情境直观化，促进陈述性知识的获得

数学探究活动是让学生在问题情境中经历发现问题，进而生成问题解决方式的过程［6］. ACT-R理论认为陈述性知识的获得有被动接受和主动建构两种方式，并不是所有的新课引入都能吸引学生的注意力，创设适当的情境有助于学生尽快地进入学习状态. 新课引入要遵循直观化原则，主要从两个方面入手：数学史和实际需要. 引入数学史的目的是让学生知道知识的出处，了解数学家的故事，激发他们学好数学的信心等非智力因素；实例引入要贴合学生固有的生活常识，而不是直接讲述某一知识点让学生记忆，要注意内容大于形式. ACT-R理论的一个基本观点是学习能力的提高可以通过简单的环节来实现，与现实生活联系后再引入新的知识点的过程，可以促进陈述性知识的获得.

2. 目标层级化，触发程序性知识的产生

数学探究活动是基于问题情境开展自主探究、合作探究并最终解决问题的过程，就是程序性知识的获取过程. ACT-R理论认为程序性知识的获取关键在于产生式规则的获得. 产生式主要依靠两个条件，一是需要一个处理某个具体目标的情境；二是需要一个处理类似目标的样例. 在学习与问题解决的过程中，每一个知识目标都被分解为一连串的子目标，而这些子目标又被分解为一连串的更小的子目标，通过目标层级分解使得产生式被触发，从而不断深入和把握原有知识结构，以便学习新的知识，完成新的经验块，产生更多的迁移能力，以程序化的形式固定下来.

3. 练习精致化，促进自动化技能的形成

数学探究活动中复杂问题的解决，都需要基本技能的流畅性. ACT-R理论认为“熟能生巧”，“熟”是提高陈述性知识激活水平和产生式强度的必要条件，即知识从陈述性转变为程序性的过程中，练习发挥着举足轻重的作用，通过大量的精致练习，动作和条件之间的反应时间大大缩短，它们之间的匹配度得到提高，程序性知识会更加自动化，ACT-R理论实际上也是“做中学”和“例中学”的理论.

本节课基于ACT-R理论的斐波那契数列教学设计，以发现斐波那契数列通项公式及其性质为主线，通过“情境背景—设计方案—小组合作—推进方案—形成成果”这一由陈述性知识转化为程序性知识的过程，促进学生敢于质疑、善于合作、勇于创新，而这恰恰是数学探究活动的价值所在.

参考文献：

［1］ 顾泠沅，鲍建生，周超. 数学学习的心理基础与过程［M］. 上海：上海教育出版社，2009.

［2］ 约翰·安德森. 认知心理学［M］. 杨清，张述祖，译. 长春：吉林教育出版社，1989.

［3］ 曾海英. 初中数学教科书中的数学探究活动分析［J］. 数学教学研究，2016，35（08）：10-15+20.

［4］ 刘伟. 基于ACT-R理论的初中数学概念课教学设计研究［D］. 上海师范大学，2014.

［5］ 叶宏秀，张贤金. 指向核心素养的微项目化学习*——以“粗盐的精制”的教学为例［J］. 化学教与学，2022（11）：59-62.

［6］ 靳玉乐. 探究教学论［M］. 重庆：西南师范大学出版社，2000.