构思想方法路径 破高考垂直难题

彭剑峰 刘存华

摘 要：立体几何是培养学生直观想象和逻辑推理的重要载体，在历年高考中呈现“占比大、失分高”的特点。课题组通过梳理学生在立体几何中的学习障碍，并对53份历年数学高考卷进行分析，根据高中课程内容构建知识网络，以知识、思想体系为核心，分类突破“空间垂直证明”的难题，从而为教师教学和学生答题提供可行性帮助。

关键词：垂直证明；知识体系；立体几何；空间垂直证明

中图分类号：G63 文献标识码：A 文章编号：0450-9889（2024）14-0097-04

《普通高中数学课程标准（2017年版2020年修订）》提出的六大核心素养中的直观想象，指的是学生利用空间想象结合几何图形的直观性来解决问题的品格与能力［1］。虽然新版教材的教学内容经过了删减，但立体几何内容在高中课程中仍然占有一席之地，考试大纲也要求“高中生需要具备理解空间中线、面的平行与垂直关系的判定定理和性质定理的能力，并能证明相关命题”。立体几何内容具有高度的抽象性和逻辑性，是培养学生逻辑推理素养的重要载体，且立体几何内容也非常丰富，具有极高的教育研究价值。特别是历年高考全国卷中均对“立体几何”进行了考查，考查题型多以“小题（选择、填空）+解答题”为主。然而，高中生立体几何的学习是否存在障碍？高考中立体几何的考查侧重点是什么？如何突破高考几何证明难题？基于这些问题，本研究通过梳理高中生立体几何学习障碍，继而对数学高考卷中的立体几何考题进行分析，结合高中课程内容提出空间垂直证明的解题思路，并以高考真题为例进行分类归纳和总结，让学生达到“以一题会一类”的目标，指导学生学会处理证明难题，以期为教师的教学提供参考和启发。

一、研究基础

（一）文献研究

以“高中立体几何学习”为主题进行检索并筛选出2017—2023年的22篇硕士论文，采用文献研究法进行研究。22篇硕士论文大多采用问卷调查、试卷测试法、访谈法对高中阶段三个年级学生进行了现状调查和分析。通过梳理上述研究我们发现，高中生立体几何学习障碍大多集中在：提取障碍（知识应用、方法选择不合理）、认知障碍（空间想象能力、逻辑推理能力水平低）、操作障碍（证明思路不清晰、作答不规范）［2］。因此，本研究提出构建知识和思想体系，旨在解决立体几何学习三大障碍。

（二）高考研究

高考作为我国选拔人才的重要方式之一，而数学学科更是在高考中发挥着举足轻重的作用。因此，研究高考试题极具价值，有利于了解高考指挥棒的方向，把握高考的重难点，明晰考试常见的出题模式。

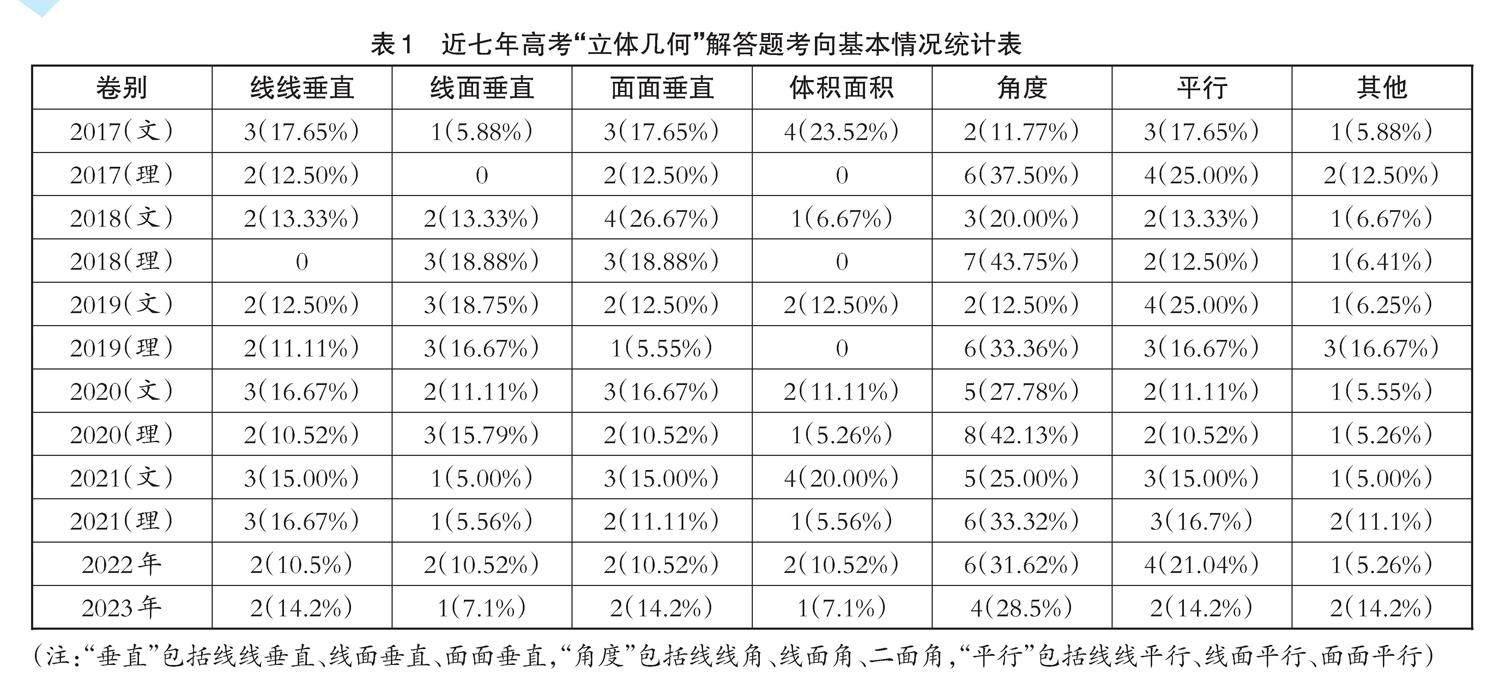
本研究选取了近七年（2017—2023年）的文科卷、理科卷的53份高考题，主要包含的卷别为全国甲卷、全国乙卷、全国新高考Ι卷、全国新高考Ⅱ卷、全国Ι卷、全国Ⅱ卷、全国Ⅲ卷、浙江卷、上海卷、北京卷、天津卷、江苏卷、山东卷，并且以其中的“立体几何”解答题为研究样本进行统计分析。因各地各卷对立体几何的考查和赋分不一致，本研究主要探究考点集中趋势、考查方向和考查难度，主要进行考点的频次统计（基本考查方向和情况如下页表1所示）。

由表1可知，文科卷的垂直证明占比为35%—53.3%，理科卷相对少一些，占比为33.3%—37.6%。但是值得关注的是，除2017年（理）、2018年（理）、2020年（理）外，其他年份对“垂直关系证明”考查的占比远高于“体积面积”“角度”“平行”“其他”四类，这说明“垂直关系证明”在高考中占有相当大的比重。通过进一步深入分析我们发现，在2017年（理）、2018年（理）、2020年（理）三次考试中，理科的第（2）小问着重考查二面角，这就是“角度”频次高的原因。从知识层面进行分析，若使用空间向量的方法，需要建立空间直角坐标系和计算点坐标，此过程需要依赖垂直的相关知识；若使用欧氏几何方法求解线面角和二面角，角度的确定和构造与线面垂直、面面垂直关系密切［3］，因此也是侧面考查垂直关系的证明和判定。

综上所述，垂直在高考立体几何中的考查比例最大，其重要性不言而喻。但是，根据上述文献研究和调查分析得知，学生的作答情况并不乐观，立体几何中的“垂直问题”应引起一线教师的重视。

（三）策略研究

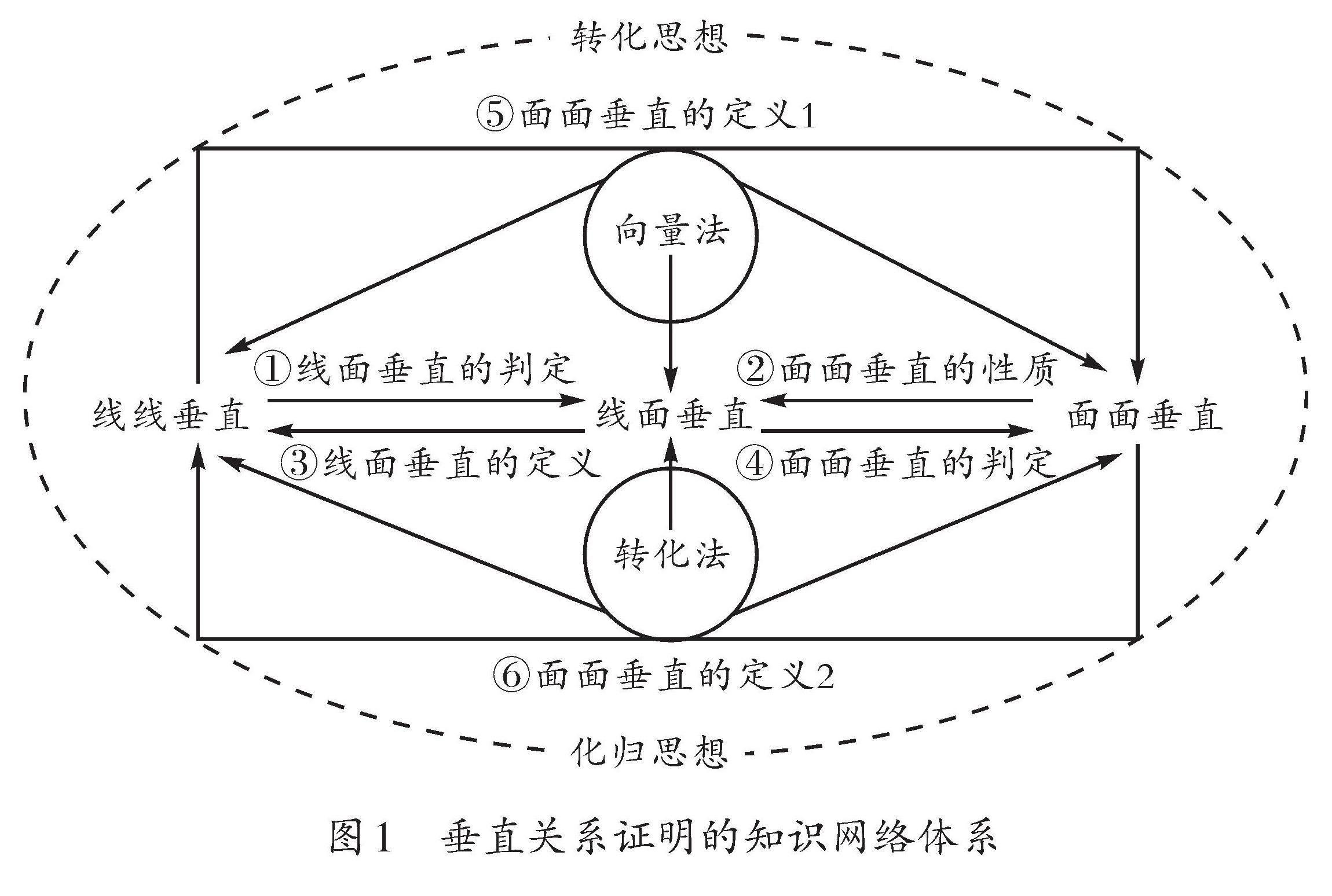
学生在学习立体几何的过程中存在诸多困难，体现为提取障碍、认知障碍和操作障碍。而高考立体几何的考查又以“垂直关系的证明”为主，所以本研究提出“通过建构知识网络体系”的方法，以解决垂直关系证明的难题（具体网络如图1所示）。

策略解析：一是构建知识网络体系，破解提取障碍。学生在教师的带领下构建知识体系，明确“线线垂直”“线面垂直”“面面垂直”之间的关联，在做题时可运用体系中的“定义”“判定”“性质”进行组合搭配，形成做题思路和方法。二是掌握知识转化关系，破解认知障碍。在转化和化归思想下，学生可在新知学习和作业练习中反复训练“线线”“线面”“面面”之间的推理过程。同时，抓住题目中的关键条件或者信息辅助解题，可逐步解决认知障碍。三是运用定义定理证明，破解操作障碍。学生在日常训练中应总结所运用的知识，并严格要求作答时结合题目条件“翻译”成定理内容，在证明过程中呈现出定义定理，以达到踩点得分的规范效果［4］。

二、试题分析

（一）“线线垂直类”题型分析

1.真题再现及解答思路分析

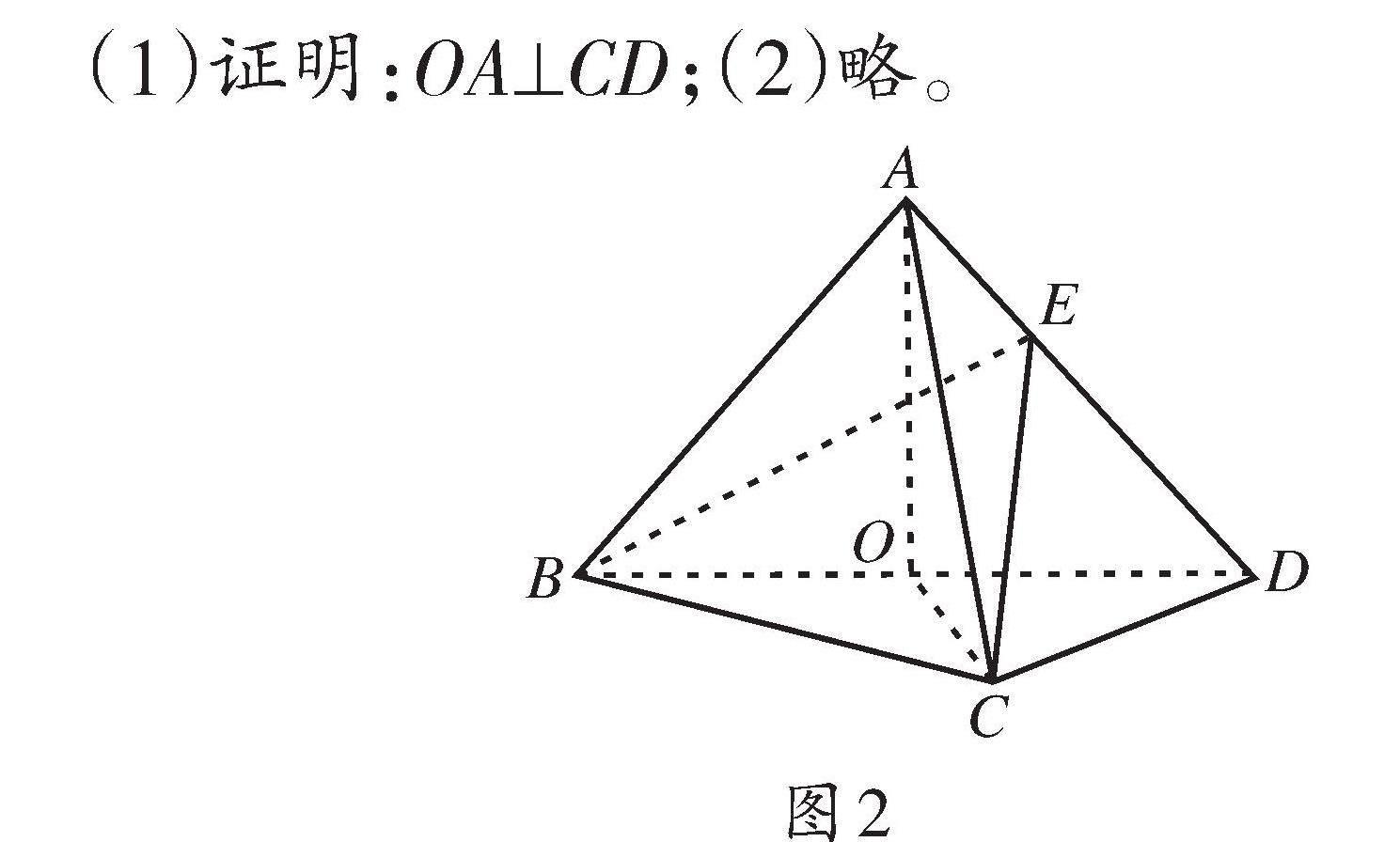
“线线垂直类”题型例题：（2021年全国新高考Ι卷第20题的第1问）如图2所示，在三棱锥A-BCD中，平面ABD⊥平面BCD，AB=AD，O为BD的中点。

（1）证明：OA⊥CD；（2）略。

2.考点及思路分析

本题考查线线垂直的证明，该证明过程秉持由复杂到简单的化归思想，欲证“线线垂直”可先从“面面垂直”入手，因此可执行图1中的“面面垂直→线面垂直→线线垂直”的证明路径。证明过程中主要关注面面垂直和中点两个条件，运用面面垂直的性质和线面垂直的定义可解（如图3所示）。

3.解题规律及方法总结

证明“线线垂直”一般有如下方法［5］。①几何法：通过“面面垂直、线面垂直、线线垂直”的路径证明（如例题1、2019年浙江卷、2019年江苏卷、2017年江苏理科卷、2021年全国文科甲卷、2020年全国Ⅲ文科卷、2018年天津文科卷）。②向量法：证明两条直线所在的向量的方向向量的数量积为0（如2021年全国理科甲卷、2020年天津文科卷）。③转化法：通过证明目标线的平行线与另一条线垂直（如2021年浙江理科卷、2020年浙江理科卷）。

（二）“线面垂直类”题型分析

1.真题再现及解答思路分析

“线面垂直类”题型例题：（2019年天津文科卷第17题第1问）如图4所示，在四棱锥P-ABCD中，底面ABCD为平行四边形，△PCD为等边三角形，平面PAC⊥平面PCD，PA⊥CD，CD=2，AD=3，棱PC的中点为N，连接DN。

（1）求证：PA⊥平面PCD；（2）略。

2.考点及思路分析

本题主要考查线面垂直，该证明运用了面面垂直的性质、线面垂直的定义和线面垂直的判定三个知识点，虽然有所辗转，但核心思路是一条直线与平面内的两条相交直线垂直，两组“线线垂直”可通过“线面垂直”“菱形对角线”“勾股定理”等途径来构造和证明（如图5所示）。

3.解题规律及方法总结

证明“线面垂直”一般有如下方法。①转化法：证明目标线的平行线垂直于平面，从而间接证明线面垂直（如2020年全国新高考卷）。②判定法：利用线面平行的判定定理证明线线垂直得到线面垂直（如2019年北京卷）。③辗转法：证明路径为“面面垂直→线面垂直→线线垂直→线面垂直”，其本质仍然是判定定理的运用，但是此类方法需要学生有完整的知识体系（如2019年天津文科卷）。④向量法：本质为证明直线的方向向量为平面的法向量，即为直线的方向向量和平面内两个不共线向量的数量积均为0（如2018年浙江文科卷）。

（三）“面面垂直类”题型分析

1.真题再现及解答思路分析

“面面垂直类”题型例题：（2019年天津文科卷第17题第1问）如图6所示，四棱锥P-ABCD的底面是矩形，PD⊥平面ABCD，PD=DC=1，AD=[2]，点M在棱BC上。

（1）若点M为棱BC的中点，证明：平面PAM⊥平面PBD；（2）略。

2.考点及思路分析

本题考查了面面垂直的证明，该证明过程主要围绕“面面垂直的判定定理”进行，关键点在其中一个平面内找到一条垂直于另外一个平面的直线，因此问题就转化为证明线面垂直和线线垂直。通过对近五年高考试题中涉及的25道面面垂直类型题进行分析，发现绝大部分题均可通过此方法进行证明（如图7所示）。

3.解题规律及方法总结

证明“线面垂直”一般有如下方法。①几何法：通过面面垂直的判定来证明，其核心是证明线面垂直，因此遵循的路径应当是“线面垂直→线线垂直→线面垂直→面面垂直”（如例题3、2021年全国新高考Ⅱ卷）。②定义法：作出二面角的平面角，进而证明该角度为90°。③向量法：证明两个平面的法向量垂直，即证明垂线的方向向量的数量积为0。④转化法：两个平行平面中的一个平面与另一个平面垂直，则另一个平面也与第三个面垂直。

三、总结反思

本研究从“学习障碍”“高考考向”出发，提出“应对策略”并运用此策略对高考垂直三大类证明进行分析，得出一般的方法和规律，给予学生建议和帮助。但教学的主场仍然在于日常课堂，因此笔者提出以下三点教学建议。

（一）加强课堂小结环节，构建知识思维网络

课堂小结在很多日常课堂中经常被冠以“草草结束”的评价，教师应充分利用课堂小结的平台与时间，运用思维导图软件，引导学生自主总结知识点、数学思想和方法，并且及时纳入单元思维导图中，帮助学生形成完备的网络体系。

（二）重视以题会类教学，提升类比迁移能力

真正做到以题会类［6］，需要在日常课堂中创设解题情境，选择典型例题作为母题教会学生“解题出发点”，即把教师脑子里面的想法嫁接给学生，不仅要教“怎么做”，更要教“怎么想”和“为什么要这样想”。母题教学之后应当选择考向考点相近的题目进行训练，让学生在熟悉的情境里运用知识、运用方法，才能达到“同类型题怎么做”的功效。

（三）更改解题教学模式，培养思路梳理能力

解题教学不仅要进行“题海战术”，还要精选例题；不仅要传授解答技巧，更要梳理思路。在习题课教学中，教师可以在讲解答案之前，提问学生解题思路，以“从哪里入手？为什么这么想？接下来该怎么做？你的整个解题运用了哪些知识点？解答这道题你有什么感悟或者经验方法？”为路径循循善诱，让学生充分发言表达，培养学生梳理思路的能力［7］。

参考文献

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2017.

［2］张娅娅.高中生立体几何学习现状调查研究［D］.西北师范大学，2020.

［3］周建锋.用三面角模型巧解2022年高考立体几何题［J］.中学数学研究（华南师范大学版），2023（1）：16-19.

［4］逯彦周，项丽红.2022年全国数学高考卷立体几何试题分析及教学思考［J］.中学教研（数学），2022（12）：40-44.

［5］宋秀云.基于“三新”背景，掌握两种方法：以立体几何为例的大单元教学［J］.中学数学研究，2023（7）：11-13.

［6］刘华为.基于知识转化 探求以题会类［J］.中学数学教学参考，2018（8）：39-42.

［7］李海东.基于核心素养的“立体几何初步”教材设计与教学思考［J］.数学教育学报，2019（1）：8-11.

注：本文系南宁市教育科学“十四五”规划2022年度C类课题“以课本题为生长点的深度学习策略与案例研究”（2022C395）的研究成果。

（责编 林 剑）

作者简介：彭剑峰，1979年生，广西梧州人，本科，一级教师，主要从事数学与应用数学、数学教育、高考数学研究；刘存华，1996年生，广西合浦人，硕士研究生，一级教师，主要从事数学教育、教育心理学研究。