自动驾驶电动车辆基于参数预测的径向基函数神经网络自适应控制

陈志勇 李攀 叶明旭 林歆悠

摘要：

针对具有不确定性的自动驾驶电动车辆的运动控制问题，提出了一种基于参数预测的径向基函数（RBF）神经网络自适应协调控制方案。首先，考虑系统参数的不确定性及外部干扰的影响，利用预瞄方法建立可表征车辆循迹跟车行为的动力学模型；其次，采用RBF神经网络补偿器对系统不确定性进行自适应补偿，设计车辆横纵向运动的广义协调控制律；之后，考虑前车车速及道路曲率影响，以车辆在循迹跟车控制过程中的能耗及平均冲击度最小为优化目标，利用粒子群优化（PSO）算法对协调控制律中的增益参数K进行滚动优化，并最终得到一系列优化后的样本数据；在此基础上，设计、训练一个反向传播（BP）神经网络，实现对广义协调控制律中增益参数K的实时预测，以保证车辆的经济性及乘坐舒适性。仿真结果证实了所提控制方案的有效性。

关键词：自动驾驶电动车辆；不确定性；径向基函数神经网络；粒子群优化算法；参数预测

中图分类号：TP242.6

DOI：10.3969/j.issn.1004132X.2024.06.004

开放科学（资源服务）标识码（OSID）：

RBF Neural Network Adaptive Control for Autonomous Electric Vehicles

Based on Parameter Prediction

CHEN Zhiyong  LI Pan  YE Mingxu  LIN Xinyou

School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou，350108

Abstract： Based on parameter prediction， a RBF neural network adaptive control scheme was proposed for the motion control problems of autonomous electric vehicles with uncertainties. Firstly， the influences of system parameter uncertainties and external interferences were considered， and a dynamic model which might reflect the tracking and following behaviors of vehicles was established by the preview method. Secondly， RBF neural network compensator was adopted to compensate system uncertainties adaptively， and a generalized coordinated control law was designed for the lateral and longitudinal motions of vehicles. Thirdly， the impacts from the front vehicle speeds and road curvatures were taken into account， and the minimization of the energy consumption and the average jerks in the tracking and following control processes were regarded as the optimization objects. Afterwards， PSO algorithm was utilized to rolling optimize the gain parameter K in the coordinated control law， and then a series of optimized sample data were obtained. Then， to ensure the economy and ride comfort of vehicles， a BP neural network was designed and trained to realize the real-time prediction of gain parameter K in the generalized coordinated control law. Simulation results validate the effectiveness of the proposed control scheme.

Key words： autonomous electric vehicle; uncertainty; radial basis function（RBF） neural network; particle swarm optimization（PSO） algorithm; parameter prediction

收稿日期：20231007

基金项目：国家自然科学基金（52272389）

0  引言

Symbol`@@燃油汽车的广泛使用不但消耗了大量的石化资源，而且还加剧了全球的环境污染。相比之下，电动汽车在经济性、环保性、能源利用率、控制灵活性等方面独具优势［1］。目前，电动汽车已开始取代燃油汽车成为人们日常出行的主要工具之一。伴随着国家未来智能交通网的构建与完善，智能化程度更高的自动驾驶电动车辆已愈发引人关注［2-4］。

无论是燃油汽车还是自动驾驶电动车辆，精确、有效的运动控制是保证其稳定、安全行驶的前提。在车辆横向运动控制方面，文献［5］利用YOLO-v3算法对车辆行驶环境进行感知，设计了一种前馈+预测线性二次型调节器（linear quadratic regulator， LQR）的控制方法；与反馈+LQR控制、LQR控制、模型预测控制（model predictive control， MPC）相比，该方法能够更好地保证车辆在复杂环境下的横向跟踪精度。文献［6］考虑车辆轮胎侧偏刚度的不确定性，提出了一种自动驾驶电动车辆的自适应约束路径跟踪控制方案，并实车验证了方案在不同工况下的可行性。文献［7］研究了一种自动驾驶车辆的主动转向鲁棒控制方法，该方法通过增益调节策略来获取适当的反馈控制增益，使车辆对系统时变参数保持一定的鲁棒性，仿真结果证实了该方案的控制性能比LQR和MPC更佳。在车辆纵向运动控制方面，人们常使用比例积分（PI）控制策略或比例积分微分（PID）控制策略进行纵向车速跟踪，此类控制策略虽结构简单，但其控制参数不易整定。为解决上述问题，文献［8］利用粒子群优化（particle swarm optimization， PSO）算法和批处理归一化方法改进了传统反向传播神经网络（back propagation neural network， BPNN），并将其用于智能车辆纵向PI控制的参数自整定中，从而提高了车辆的纵向运动精度。文献［9］为了保证智能车辆在参数不确定、存在外部干扰等因素影响下的纵向行驶精度，提出了一种动态滑模控制与径向基函数（radial basis function， RBF）神经网络补偿控制相结合的纵向运动控制方案，仿真及实车测试结果均表明控制方案具有鲁棒性。

自动驾驶电动车辆基于参数预测的径向基函数神经网络自适应控制——陈志勇  李  攀  叶明旭等

中国机械工程 第35卷 第6期 2024年6月

鉴于实际车辆模型具有高度的非线性及强耦合性，单一的横向或纵向控制方法往往难以保证系统的全局控制性能，为此，许多学者开始探究车辆的横纵向综合协调控制问题。针对模型精确已知工况，文献［10］通过引入松弛因子并附加考虑前轮侧偏角约束，提出了一种车辆横向运动的改进MPC控制策略，而混合PID控制策略用于保证车辆在不同路面条件下的纵向速度跟踪。为提高四轮独立驱动车辆在极端工况下的横纵向运动稳定性，文献［11］给出了一种非线性MPC控制策略。文献［12］考虑车辆侧偏刚度不确定影响，为自动驾驶车辆设计了PSO-PID横向控制器和线性参变MPC纵向控制器，并通过仿真实验验证了方案的有效性。文献［13］为应对外部干扰及参数摄动影响，采用无偏置MPC控制方案来处理自动驾驶车辆的横纵向耦合控制问题。

但以上研究大多只专注于解决车辆横纵向运动控制问题，较少兼顾车辆在控制过程中的经济性和舒适性，为此，本文综合考虑上述因素，针对具有不确定性自动驾驶电动车辆提出了一种基于参数预测的RBF神经网络自适应协调控制方案。首先，利用预瞄方法建立车辆的循迹跟车动力学模型；其次，基于RBF神经网络补偿技术为车辆的横纵向运动设计广义协调控制律；接着，考虑前车车速及道路曲率影响，以车辆在控制过程中的能耗及平均冲击度最小为优化目标，利用粒子群算法对方案中的增益参数进行滚动优化，并将最终优化得到的一系列样本数据用于BP神经网络的学习与训练；之后，将训练好的BP神经网络用于广义协调控制律中增益参数的实时预测，以保证车辆的经济性和乘坐舒适性。

1  系统描述

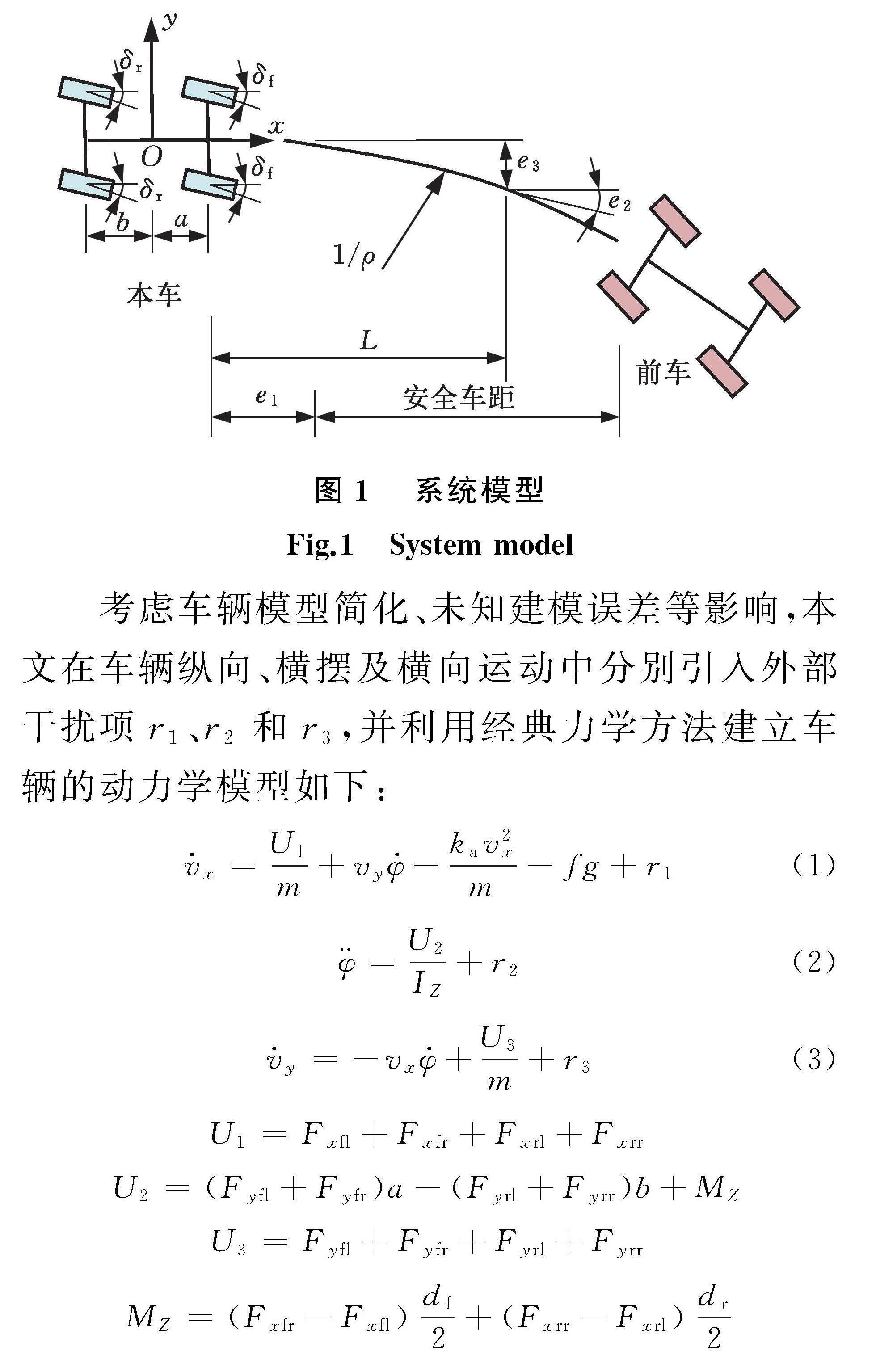
以做平面运动的自动驾驶电动车辆为研究对象，建立了基于预瞄方法描述的车辆循迹跟车模型，如图1所示。图中，Oxy为建立在车辆质心O处的车辆坐标系；a、b分别为车辆前后轴到车辆质心O的距离；δf为前轮转角，δr为后轮转角；e1为前车与自动驾驶车辆的纵向偏差，e2为预瞄点处车辆中心线与道路中心线的方位偏差，e3为预瞄点到道路中心线的横向偏差；ρ为道路中心线曲率；L为预瞄距离。

考虑车辆模型简化、未知建模误差等影响，本文在车辆纵向、横摆及横向运动中分别引入外部干扰项r1、r2和r3，并利用经典力学方法建立车辆的动力学模型如下：

v·x=U1m+vyφ·－kav2xm－fg+r1（1）

φ¨=U2IZ+r2（2）

v·y=－vxφ·+U3m+r3（3）

U1=Fxfl+Fxfr+Fxrl+Fxrr

U2=（Fyfl+Fyfr）a－（Fyrl+Fyrr）b+MZ

U3=Fyfl+Fyfr+Fyrl+Fyrr

MZ=（Fxfr－Fxfl）df2+（Fxrr－Fxrl）dr2

式中，Fxq（q=fl，fr，rl，rr）为车辆各轮胎的纵向驱动力/制动力；Fyq为车辆各轮胎的横向力；下标fl、fr、rl、rr分别表示车辆左前轮、右前轮、左后轮和右后轮；vx、vy分别为车辆的纵向速度和横向速度；φ为车辆的横摆角；m为车辆的总质量；IZ为车辆的转动惯量；f为地面的滚动阻力系数；ka为空气阻力系数；g为重力加速度；MZ为附加横摆力矩；df为前轴轮距；dr为后轴轮距。

根据文献［14］，前车与自动驾驶车辆的纵向偏差变化率e·1、预瞄点处车辆中心线与道路中心线的方位偏差变化率e·2及预瞄点到道路中心线的横向偏差变化率e·3可分别表示为

e·1=vp－vx－τhv·p（4）

e·2=vxρ－φ·（5）

e·3=vxe2－vy－φ·L（6）

式中，vp为前车速度；τh为跟车时距。

综合式（1）～式（6），可导出车辆的循迹跟车动力学模型：

Me¨+G+Mτ=U（7）

U=（U1，U2，U3）T

其中，U为系统的广义控制列向量;M=diag（g1，g2，g3），且g1=－m，g2=－IZ，g3=－m；e=（e1，e2，e3）T；τ=（τ1，τ2，τ3）T且τ1=r1，τ2=r2－ρr1，τ3=r2L+r3－r1e2；G=（G1，G2，G3）T且G1=mv·p－mvyφ·+kav2x+fmg－mτhv¨p，G2=U1mρIZ+vyφ·ρIZ－kav2xmρIZ－fgρIZ，G3=U1e2+

mvyφ·e2－kav2xe2－fmge2+mvxe·2+mvxφ·－U2IZmL。

考虑车辆质量及转动惯量的不确定性，用m^和I^Z分别表示车辆的估计质量及估计转动惯量，用Δm和ΔIZ分别表示车辆真实质量与估计质量之间的差值、真实转动惯量与估计转动惯量之间的差值，则存在m=m^+Δm，IZ=I^Z+ΔIZ。重新整理式（7），得

M^e¨+G^+M^τd=U（8）

其中，M^、G^分别为M和G对应的估计值，M^=diag（g^1，g^2，g^3），G^=（G^1，G^2，G^3）T；

τd为新的综合扰动列向量，

τd=（τd1，τd2，τd3）T，且τdi=

τi+

Δgie¨i+ΔGi+Δgiτig^i，i=1，2，3，Δgi=

gi－

g^i，

ΔGi=Gi－G^i。

2  基于参数预测的RBF神经网络控制

为实现具有不确定性自动驾驶电动车辆的横纵向协调运动控制，并保证车辆在控制过程中的经济性及乘坐舒适性，本文提出了一种基于参数预测的RBF神经网络自适应控制方案。

2.1  横纵向运动的广义协调控制律

利用系统跟踪误差ei（i=1，2，3）及误差变化率e·i构造滑模函数：

si=ciei+e·i（9）

其中，常数ci>0。

对式（9）求导，可得

s·i=cie·i+e¨i（10）

基于RBF神经网络自适应补偿技术，初步设计车辆横纵向运动的广义协调控制律：

Ui=（－Ksi－εsgn（si）－cie·i+τ^di）g^i+G^i（11）

其中，K为适当选取的增益参数，K>0；ε为滑模切换项常数，ε>0；τ^di为用于消除系统不确定性影响的RBF神经网络补偿控制器输出［15］。

将式（11）中的RBF神经网络设计为一类单隐含层、双输入单输出的网络结构，设网络隐含层有n个神经元节点，输入量选为xi=（si，s·i）T，则未知量τdi的理想逼近表达式可描述为

τdi=（w*i）Th（xi）+i（12）

其中，w*i为神经网络的理想权值列向量，w*i∈Rn×1；h（xi）为网络隐含层激活函数组成的列向量，h（xi）=（h1（xi），h2（xi），…，hn（xi））T，且

hj（xi）=exp（－‖xi－μj‖2σ2j）为第j（j=1，2，…，n）个隐含层神经元节点的径向基函数，μj、σj分别为径向基函数的中心值矢量及宽度，μj=（μj1，μj2）T；i为神经网络的逼近误差，且|i|<-，-为一个小常数，->0。

神经网络的实时输出τ^di可相应地表示为

τ^di=w^Tih（xi）（13）

其中，w^i为神经网络的实时权值列向量。

定理  对于动力学方程式（8），若广义协调控制量Ui（i=1，2，3）由控制律式（11）确定，并同时采用如下权值更新策略：

w·^i=－1γsih（xi）（14）

则系统跟踪误差ei将渐近稳定地趋向于零。其中，γ为调节系数，γ>0。

证明  选取如下Lyapunov函数：

Vi=12s2i+12γw～Tiw～i（15）

w～i=wi－w^i

对式（15）求导，并结合式（8）～式（14），有

V·i=sis·i+γw～Tiw·～i=

si（－Ksi－εsgn（si）+

τ^di－τdi）－γw～Tiw·^i=

si［－Ksi－εsgn（si）－

（w～Tih（xi）+i）］－γw～Tiw·^i

=

si（－Ksi－εsgn（si）－

i）－w～Ti（sih（xi）+γw·^i）

=

－Ks2i－si（εsgn（si）+i）（16）

对系统进行稳定性分析如下：当si和i同号时，V·i<0成立；当si和i异号时，只要使ε>|-|，则V·i<0依然成立。显然，此时系统跟踪误差ei将渐近稳定地趋向于零。

2.2  增益参数K的BP神经网络预测

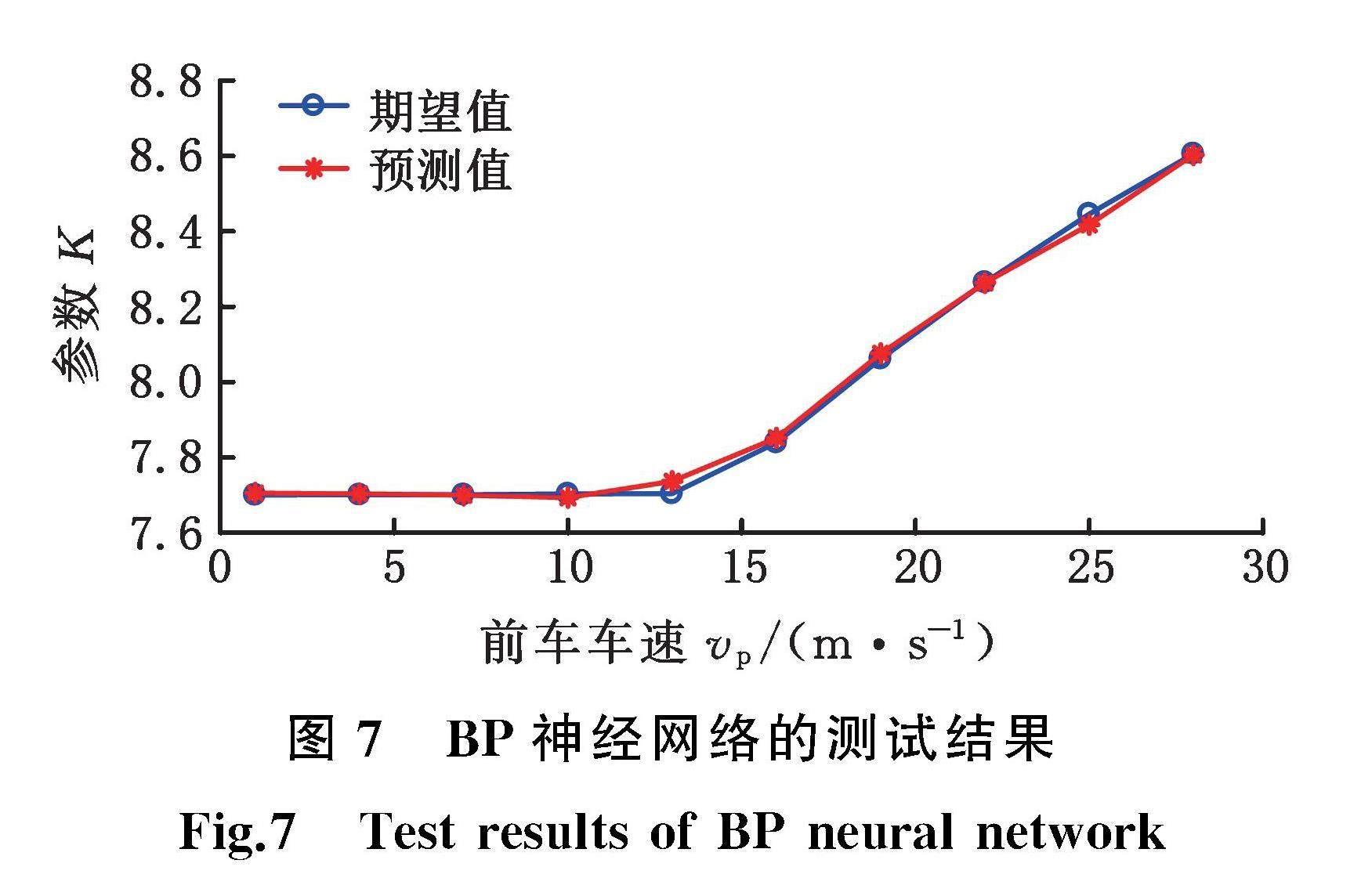
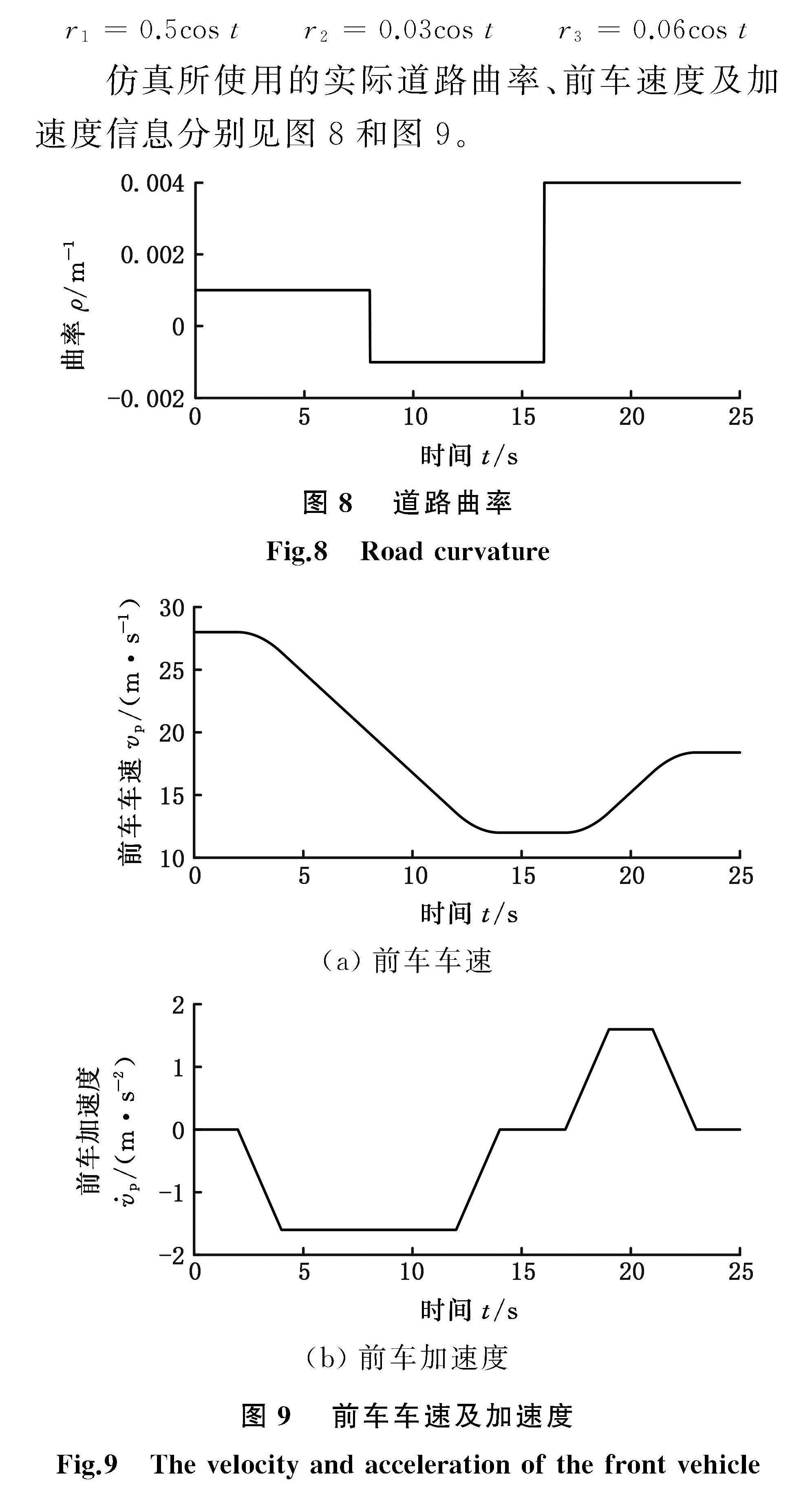
结合式（11）及式（16）可知，在保持其他控制参数不变的情况下，基于RBF神经网络补偿的广义协调控制律的控制性能与参数K的取值密切相关。一般来说，K取值越大，系统广义控制量Ui的初值就越大，误差的收敛速度就越快，但过快地实施车辆循迹跟车控制将会给车辆的乘坐舒适性带来不利影响；反之，K取值越小，系统广义控制量Ui的初值越小，系统误差的收敛速度越慢，此时车辆的循迹跟车能力、能耗等也会受到不同程度的影响。因此，选取适当的K值有助于兼顾车辆的循迹跟车能力、能耗及乘坐舒适性，使控制器更符合安全、低碳、舒适的驾驶理念。考虑到动力学方程式（8）中包含有未来不断变化的前车车速和道路曲率信息，为更好地保证车辆的整体控制性能，本节将结合粒子群优化算法，着重研究不同前车车速及道路曲率对广义协调控制律中增益参数K取值的影响，并设计、训练一个BP神经网络来实时预测增益参数K。

2.2.1  基于粒子群优化的BP神经网络样本获取

为保证实际行车安全，本节对在不同曲率道路上行驶的前车车速vp作如下限定：当道路曲率|ρ|较小时，即0≤｜ρ｜≤ρmin时，前车的最高车速限定为vmax1；当道路曲率｜ρ｜较大时，即ρmin≤｜ρ｜≤ρmax时，前车的最高车速限定为vmax2，且vmax2

基于粒子群优化算法，BP神经网络每一个学习样本的基本获取流程如图2所示。

首先，对2.1节所提广义协调控制律（式（11））中的待优化参数K进行赋初值，并初始化粒子群；其次，在选定的道路曲率和前车车速下，结合所提协调控制方案对自动驾驶车辆进行一段时间（T）内的循迹跟车控制；之后，以车辆纵向驱动能耗及平均冲击度最小为优化目标，采用粒子群算法对参数K进行滚动优化，以最终获得在指定道路曲率、前车车速下参数K的最优取值。

图2所示粒子群优化算法主要是通过粒子跟踪个体最优值和全局最优值来不断迭代更新每个粒子的速度和位置，从而找到最优解，其具体设计如下：

定义一个粒子群Y=（y1，y2，…，yn1）T，yl表示第l（l=1，2，…，n1）个粒子的位置，n1表示粒子的总数。由于本文优化的对象只有参数K，故取yl=l，l表示第l个粒子的K值；v-l表示第l个粒子的速度，其上限值设为v-l_max。在对每一个特定道路曲率和特定前车车速下的参数K进行优化前，粒子群算法会对粒子群中的每个粒子进行初始化，即将每个粒子的位置初始化为l_in，每个粒子的速度初始化为

v-l_in=－v-l_max+2v-l_maxdrand（17）

其中，drand为［0，1］范围内的随机数。此外，将粒子群的最大迭代次数设定为nc，并以此作为粒子群迭代优化是否结束的依据。

为兼顾自动驾驶车辆循迹跟车控制过程中的系统能耗［16-17］及乘坐舒适性［18］，在粒子群优化的每一次迭代过程中考虑车辆的纵向加速度约束，并通过如下方式计算每个粒子的适应度：

JZ=ξJNJN_max+（1-ξ）JCJC_max  |ax|≤a-x_max

JZ_max|ax|>a-x_max（18）

JN=Edrive－Ebrake=

∑Tt=0｜Ft｜vxΔtηmηd－∑Tt=0｜Fb｜vxΔtηb

JC=∑Tt=0｜a·x｜nd  nd=T+ΔtΔt

式中，ξ为权衡车辆能耗的权重因子，1－ξ为权衡车辆平均冲击度的权重因子；JN、JN_max分别表示在规定仿真时长T内车辆能耗及其上限值；JC、JC_max分别表示在规定仿真时长T内车辆所受平均冲击度及其上限值；ax为车辆的纵向加速度；a-x_max为纵向加速度约束上限值；Ft为驱动力，Edrive为驱动能耗；Ebrake为系统回收的制动能量；驱动工况（即U1>0）下，Ft=U1；Fb为制动力，制动工况（U1<0）下，Fb=U1；ηm为机械传动效率；ηd为电动效率；ηb为能量回收效率；Δt为采样时间；nd为在规定仿真时长T内的采样次数；JZ_max为一个足够大的正常数，用于剔除掉那些在优化过程中不符合纵向加速度约束的粒子。

为保证粒子群算法的收敛性，本文将第l个粒子搜索过的最小适应度值作为其个体最优值pbest_l，将种群搜索过的最小适应度值作为全局最优值gbest，并采用如下方式对其速度及位置进行实时更新：

v-l（k）=ωpv-l（k－1）+C1R1（pbest_l－yl（k－1））+

C2R2（gbest－yl（k－1））（19）

yl（k）=yl（k－1）+v-l（k）（20）

式中，k为迭代次数；ωp为用于控制前一速度对当前速度影响的动力常量，ωp≥0；C1、C2为学习因子，C1≥0，C2≥0；R1、R2为服从［0，1］上均匀分布规律的伪随机数。

为了获得足够多的小道路曲率下的样本数据，在0≤｜ρ｜≤ρmin范围内由小到大选取χ个道路曲率ρ1，ρ2，…，ρχ，在0～vmax1速度范围内由小到大选取η个前车车速vp1，vp2，…，vpη。针对每种道路曲率ρn′（n′=1，2，…，χ）及每种前车车速vpi′（i′=1，2，…，η），利用图2所示流程进行仿真控制及粒子群优化操作，最终得到在道路曲率ρn′、前车车速vpi′下参数K的最优取值Kn′i′。遍历所有道路曲率和前车车速组合后，最终可以得到小曲率情况下的χ×η组样本数据，即

{{（ρ1，vp1），K11}，{（ρ1，vp2），K12}，…，{（ρ1，vpη），K1η}，{（ρ2，vp1），K21}，{（ρ2，vp2），K22}，…，{（ρ2，vpη），K2η}，…，{（ρχ，vp1），Kχ1}，{（ρχ，vp2），Kχ2}，…，{（ρχ，vpη），Kχη}}

上述样本数据的集合记为样本数据集{Aρ}。

为获得足够多的较大道路曲率下的样本数据，可以在ρmin≤｜ρ｜≤ρmax范围内由小到大选取ζ个道路曲率ρ′1，ρ′2，…，ρ′ζ，在0～vmax2速度范围内由小到大选取个前车车速v′p1，v′p2，…，v′p。针对每种道路曲率ρ′m′（m′=1，2，…，ζ）及每种前车车速v′pj′（j′=1，2，…，），利用图2所示流程进行仿真控制及粒子群优化操作，最终得到在道路曲率ρ′m′、前车车速v′pj′下参数K的最优取值K′m′j′。遍历所有道路曲率和前车车速组合，最终可以得到较大曲率情况下的ζ×组样本数据，即

｛{（ρ′1，v′p1），K′11}，{（ρ′1，v′p2），K′12}，…，{（ρ′1，v′p），K′1}，

{（ρ′2，v′p1），K′21}，{（ρ′2，v′p2），K′22}，…，{（ρ′2，v′p），K′2}，…，{（ρ′ζ，v′p1），K′ζ1}，{（ρ′ζ，v′p2），K′ζ2}，…，{（ρ′ζ，v′p），K′ζ}｝

上述样本数据的集合记为样本数据集{A′ρ}。

于是，样本数据集{Aρ}和数据集{A′ρ}将共同作为本文后续BP神经网络的学习样本。

2.2.2  BP神经网络的设计与训练

为了实现在不同道路曲率及前车车速下控制律（式（11））中增益参数K的自适应预测，本节将基于2.2.1节得到的样本数据，设计、训练一个BP神经网络，并用它来建立道路曲率、前车车速与参数K近似最优值之间的非线性映射关系。如图3所示，BP神经网络主要由输入层、隐含层及输出层构成，并经由网络预测误差的反向传播来不断调整神经网络的权重和偏置，进而使得网络预测值不断逼近期望值。

由于输入量为道路曲率和前车车速，输出量为参数K的预测值，故BP神经网络的输入层神经元节点数nin取为2，输出层神经元节点数nout取为1；隐含层的神经元节点数nh可参考经验公式选取［19］：

nh=nin+nout+αx（21）

其中，αx为1～10之间的整数。

神经网络隐含层激活函数采用Tansig函数：

y=1－exp（－x）1+exp（－x）（22）

输出层激活函数采用Purelin函数：

y=x（23）

BP神经网络的训练函数采用Trainlm函数，其训练次数ntr、学习速率rle及训练目标精度ta根据实际情况进行合理设定。

利用2.2.1节得到的样本数据对上述BP神经网络进行离线训练，以得到BP神经网络的理想权重和偏置［20］。再通过类似2.2.1节的样本获取操作得到一系列测试样本，并利用这些样本对前述BP神经网络预测精度进行测试与验证。最后，将最终训练、测试好的BP神经网络用于广义协调控制律式（11）中增益参数K的实时预测，并得到如下改进后的广义协调控制律：

Ui=（－KBPsi－εsgn（si）－cie·i+τ^di）g^i+G^i（24）

式中，KBP为BP神经网络实时预测得到的K值。

观察式（24）可知，只要给定某时刻的前车车速和道路曲率，BP神经网络就能对广义协调控制律式（11）中参数K进行实时预测，并给出其相对最优值。

3  车辆各轮胎驱动力/制动力及转角计算

假设车辆驱动力/制动力采用前后轴正比于轴荷且同轴左右轮均匀分配的方式［21］，此时MZ=0，则可得各轮胎的纵向驱动力/制动力分别为

Fxfl=Fxfr=12FzfFzf+FzrU1 （25）

Fxrl=Fxrr=12FzrFzf+FzrU1（26）

Fzf=m（gb－axhc）a+b

Fzr=m（ga+axhc）a+b

式中，Fzf为前轴轴荷；Fzr为后轴轴荷；hc为车辆质心高度。

车辆各轮胎的横向力可近似描述为

Fyfl=Fyfr=－Cf（vy+aφ·vx－δf）（27）

Fyrl=Fyrr=－Cr（vy－bφ·vx－δr）（28）

式中，Cf、Cr分别为前轮及后轮侧偏刚度。

根据式（1）～式（3）中U2和U3的定义，车辆各轮胎的横向力又可表示为

Fyfl=Fyfr=U32－aU3－U22（a+b）（29）

Fyrl=Fyrr=aU3－U22（a+b）（30）

将式（29）、式（30）分别代入式（27）、式（28），可求出车辆前轮转角δf、后轮转角δr，即

δf=bU3+U22（a+b）Cf+vy+aφ·vx （31）

δr=aU3－U22（a+b）Cr+vy－bφ·vx（32）

4  仿真验证

4.1  仿真模型及其控制器参数设定

为了验证本文所提基于参数预测的RBF神经网络自适应控制方案的有效性，本节对图1所示系统进行仿真试验研究。仿真所使用的自动驾驶车辆及相关系统参数列于表1。

设车辆的质量及转动惯量的估计值分别为

m^=1424 kg  I^Z=2000 kg·m2

外部干扰选取为

r1=0.6cos t m/s2  r2=0.05cos t rad/s2

r3=0.1cos t m/s2

仿真时，设自动驾驶车辆相对于前车的初始纵向偏差e1（0）=0.6 m，车辆相对于参考路径的初始方位偏差e2（0）=0.02 rad，初始横向偏差e3（0）=0.1 m；车辆的初始纵向车速与前车初始纵向车速相同，即vx（0）=vp（0），车辆的初始横向车速vy（0）=0，初始横摆角速度φ·（0）=0；预瞄距离L=10 m，跟车时距τh=2 s。

除文中拟预测的增益参数K外，2.1节所提广义协调控制律中的控制参数设为：ε=0.002，c1=c2=c3=0.5，n=40，μj=（2，2）T（j=1，2，…，n），σj=15，γ=0.6。

2.2节中粒子群优化算法的参数设为：n1=6，l_in=3，v-l_max=0.8，nc=50，ξ=0.5，JN_max=2×105 J，JC_max=10 m/s3，JZ_max=10，a-x_max=3.5 m/s2，T=6 s，Δt=0.02 s， ωp=0.8，C1=C2=1.5，ηm=0.9，ηd=0.8，ηb=0.8。

BP神经网络的训练参数设为：nh=10，ntr=1000，rle=0.01，ta=10－5。

4.2  BP神经网络的样本获取、训练与测试试验

考虑不同曲率道路下的车速限制，设2.2.1节中的小曲率阈值ρmin=0.001 m－1，小曲率下的最大车速vmax1=30 m/s；曲率上限值ρmax=0.005 m－1，大曲率下的最大车速vmax2=20 m/s。在0≤｜ρ｜≤ρmin中选取ρ1=－0.001 m－1，ρ2=0，ρ3=0.001 m－1这3组（χ=3）较小的道路曲率，并在每组道路曲率下每间隔0.5 m/s选取60组（η=60）前车车速，即vp1=0.5 m/s，vp2=1 m/s，…，vp60=30 m/s；在ρmin≤｜ρ｜≤ρmax中选取ρ′1=－0.005 m－1，ρ′2=－0.003 m－1，ρ′3=0.003 m－1，ρ′4=0.005 m－1这4组（ζ=4）较大的道路曲率，并在每组道路曲率下间隔0.5 m/s选取40组（=40）前车车速，即v′p1=0.5 m/s，v′p2=1 m/s，…，v′p40=20 m/s。

针对前述每组道路曲率及前车车速，在规定时间T=6 s内，结合2.1节所提广义协调控制方案对车辆进行循迹跟车仿真控制，其间采用粒子群算法对参数K进行滚动优化，以最终获取每组道路曲率和前车车速下所对应的参数K的最优值，并将其作为BP神经网络的训练样本。待遍历完所有道路曲率和前车车速组合后，得到图4所示的不同道路曲率和不同前车车速下参数K的最优值曲线。从图4中不难看出，经过粒子群算法优化后，广义协调控制律中的增益参数K在7.65～8.79之间选取较为合适；对于9 m/s以下的前车车速，不同道路曲率对参数K最优值的选取影响很小；对于9 m/s以上的前车车速，参数K的最优值将随着道路曲率和前车车速的增大而相应增大。

以道路曲率ρ=0.001 m－1、前车车速vp=24 m/s为例（图4中标注的A点），在该道路曲率和前车车速下，采用粒子群算法对参数K（K初始值取为3，即l_in=3）进行滚动优化，经迭代优化50次（nc=50）后，参数K和适应度JZ随迭代次数的变化情况如图5所示，经滚动优化后的参数K最优值为8.36，对应的适应度JZ为0.3985。将优化前的参数K=3和优化后的参数K=8.36分别代入控制律式（11）后，重新对车辆进行耗时6 s的循迹跟车仿真控制，所得系统跟踪误差对比如图6所示。由仿真对比结果可以看出，优化后的增益参数K可以更好地兼顾车辆的横纵向运动控制性能。

利用图4给出的样本数据对2.2.2节提出的BP神经网络进行训练，直至达到设定的目标训练次数或目标训练精度后结束训练，最终得到训练好的BP神经网络权重和偏置。

为进一步检验BP神经网络的预测能力，本文还需使用另一组样本数据对网络加以测试。为此，另外给定一个道路曲率ρ=0.0005 m－1，在该道路曲率下每间隔3 m/s选取10组前车车速，即vp1=1 m/s，vp2=4 m/s，…，vp10=28 m/s等，针对选取好的每组道路曲率及前车车速，同样通过粒子群算法对参数K进行滚动优化，以获取每组道路曲率和前车车速下所对应的参数K的最优值。本文将此处得到的10组样本数据作为BP神经网络测试样本的真实值使用。将道路曲率ρ=0.0005 m－1及前述每组前车车速输入到已经训练好的BP神经网络之中进行预测，以获取10组测试样本所对应参数K的预测值。图7给出了10组测试样本预测值和真实值的拟合情况，经计算得到对应的网络拟合均方根误差为0.015。此测试结果表明，所提BP神经网络能够在不同道路曲率和前车车速下实现对参数K的有效预测。

4.3  改进协调控制方案验证及分析

为验证所提控制方案的有效性，本节将利用改进协调控制方案（式（24））及原协调控制方案（式（11））对系统进行仿真对比试验研究。改进方案的增益参数KBP采用BP神经网络进行实时预测，而原方案中的增益参数K则试凑了4个大小不同的值来加以比较，即K=2.5，K=4，K=6，K=14。方案中的其他控制参数及系统初始条件设定与4.1节保持一致。仿真时，重设系统的外部干扰为

r1=0.5cos t  r2=0.03cos t  r3=0.06cos t

仿真所使用的实际道路曲率、前车速度及加速度信息分别见图8和图9。

图10给出开启及关闭RBF神经网络补偿器时所提改进控制方案得到的系统跟踪误差响应，以及开启RBF神经网络补偿器时原控制方案在4个不同增益参数K取值下得到的系统跟踪误差响应。图中，NNO表示开启RBF神经网络补偿器情形，NNC表示关闭RBF神经网络补偿器情

形。表2详细列出了在NNO情形下两种控制方案得到的系统驱动能耗JN、平均冲击度JC及最大纵向加速度ax_max的对比结果。

由图10可知，若关闭改进控制方案中的RBF神经网络补偿器，则自动驾驶车辆将难以在系统外部干扰及惯性参数不确定性影响下实现其预期的循迹跟车控制，此时系统各跟踪误差将在零附近上下振荡，且稳态下的最大纵向距离偏差e1为-0.19 m，最大方位偏差e2为-0.0045 rad，最大横向偏差为0.11 m。当开启RBF神经网络补偿器后，所提改进控制方案则可使系统跟踪误差渐近稳定地向零收敛，且稳态下的最大纵向距离偏差e1为0.018 m，最大方位偏差e2为0.001 rad，最大横向偏差e3为0.008 m。可见，本文所提RBF神经网络补偿器可以有效补偿系统外部干扰及参数不确定性影响，实现自动驾驶车辆更为精确的循迹跟车控制。

综合分析图10及表2可知，在RBF神经网络补偿器开启的情况下，原控制方案和改进控制方案虽然都可以使车辆的纵向距离偏差e1、方位偏差e2及横向偏差e3最终收敛到零附近的小邻域内，但其所表现出来的控制性能却大不相同。对于原控制方案，当K取值较小时（K=2.5），自动驾驶车辆的系统跟踪误差在收敛初期会出现较大幅度的振荡，车辆相应的驱动能耗及所受平均冲击度均处于较高水平；增大K值后（K=4），系统误差在收敛初期的波动将随之减小，车辆的能耗和平均冲击度也出现一定幅度的降低；再次增大K值后（K=6），系统跟踪误差的收敛速度将变得更快、更为平缓，此时车辆的能耗和平均冲击度将处于相对较低的水平；当K取值更大时（K=14），车辆的能耗和平均冲击度变化不大，但车辆最大纵向加速度却超出仿真预设的上限阈值（a-x_max=3.5 m/s2）达到3.82 m/s2。与原控制方案K=2.5、K=4和K=6相比，改进控制方案得到的车辆驱动能耗则分别下降了8.1%、3.5%和1.1%，平均冲击度分别下降了37.4%、15.7%和4.5%，有效保证了车辆的经济性和乘坐舒适性。可见，改进控制方案通过BP神经网络对参数KBP进行实时预测，能够较好地使车辆在纵向加速度约束范围内有效地完成循迹跟车控制，同时确保其驱动能耗及所受平均冲击度均相对最优。

图11为采用改进控制方案得到的KBP变化曲线，参数KBP能够根据前车车速和道路曲率实时调整，使得控制方案具有更好的适应性和鲁棒性。

图12、图13分别为采用改进控制方案得到的车辆总纵向驱动力/制动力响应曲线以及车辆前后轮转角响应曲线。图12、图13中的系统各响应曲线均较为光滑、平稳，说明所提改进控制方案

可以根据不同的道路曲率及前车车速为自动驾驶电动车辆提供更趋合理、有效的纵向驱动力/制动力及前后轮转角控制。

图14为改进控制方案下车辆的横向速度vy、质心侧偏角β（β≈vy/vx）和横摆角速度φ·等运动状态响应曲线。由图14可知，改进控制方案可以将车辆横向速度、质心侧偏角和横摆角速度变化幅值控制在较小的范围内，从而有效保证车辆在循迹跟车过程中的稳定性和舒适性。

5  结论

本文提出了一种基于参数预测的RBF神经网络自适应协调控制方案，旨在消除系统不确定性对自动驾驶电动车辆横纵向运动的影响，在有效实现车辆横纵向运动控制的同时，保证车辆的经济性及乘坐舒适性。利用预瞄方法建立了系统的动力学模型，基于RBF神经网络补偿技术构建了车辆横纵向运动的广义协调控制方案，结合前车车速及道路曲率信息，使用BP神经网络对广义协调控制律中的增益参数K进行了实时预测，进而得到了改进后的RBF神经网络自适应协调控制方案。仿真结果表明，所提改进控制方案能够使自动驾驶电动车辆在系统不确定性影响下实现其预期的循迹跟车控制，同时又可保证期间车辆的能耗及平均冲击度均处于较低水平。

参考文献：

［1］  林歆悠， 周斌豪， 夏玉田. 融合动态能耗与路网信息的电动汽车充电路径规划策略［J］.中国机械工程， 2021， 32（6）：705-713.

LIN Xinyou， ZHOU Binhao， XIA Yutian. Charging Path Planning Strategy of Electric Vehicles with Integrating Dynamic Energy Consumption and Network Information［J］. China Mechanical Engineering， 2021， 32（6）：705-713.

［2］  LEBROUHI B E， KHATTARI Y， LAMRANI B， et al. Key Challenges for a Large-scale Development of Battery Electric Vehicles：a Comprehensive Review［J］. Journal of Energy Storage， 2021， 44：103273.

［3］  KUMAR M S， REVANKAR S T. Development Scheme and Key Technology of an Electric Vehicle：an Overview［J］. Renewable and Sustainable Energy Reviews， 2017， 70：1266-1285.

［4］  MA S C， XU J H， FAN Y. Characteristics and Key Trends of Global Electric Vehicle Technology Development：a Multi-method Patent Analysis［J］. Journal of Cleaner Production， 2022， 338：130502.

［5］  YANG T ， BAI Z W， LI Z Q，et al .Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm［J］.Actuators， 2021， 10（9）：228.

［6］  ZHANG Y H， WANG W D， WANG W， et al. An Adaptive Constrained Path Following Control Scheme for Autonomous Electric Vehicles［J］. IEEE Transactions on Vehicular Technology， 2022， 71（4）：3569-3578.

［7］  ZHANG W. A Robust Lateral Tracking Control Strategy for Autonomous Driving Vehicles［J］. Mechanical Systems and Signal Processing， 2021， 150：107238.

［8］  梁旺， 秦兆博， 陈亮， 等. 基于改进 BP 神经网络的智能车纵向控制方法［J］. 汽车工程， 2022， 44（8）：1162-1172.

LIANG Wang， QIN Zhaobo， CHEN Liang， et al. Longitudinal Control Method of Intelligent Vehicles Based on the Improved BP Neural Network［J］. Automotive Engineering， 2022， 44（8）：1162-1172.

［9］  赵健， 杜金朋， 朱冰， 等. 基于自适应动态滑模控制的智能汽车纵向巡航控制［J］. 汽车工程， 2022， 44（1）：8-16.

ZHAO Jian， DU Jinpeng， ZHU Bing， et al. Longitudinal Cruise Control of Intelligent Vehicles Based on Adaptive Dynamic Sliding Mode Control［J］. Automotive Engineering， 2022， 44（1）：8-16.

［10］  SHI P C， LI L， NI X， et al. Intelligent Vehicle Path Tracking Control Based on Improved MPC and Hybrid PID［J］. IEEE Access， 2022， 10：94133-94144.

［11］  LI Z H， WANG P， CAI S， et al. NMPC-based Controller for Vehicle Longitudinal and Lateral Stability Enhancement under Extreme Driving Conditions［J］. ISA Transactions， 2023， 135：509-523.

［12］  KEBBATI Y， OUFROUKH N A， VIGNERON V， et al. Coordinated PSO-PID Based Longitudinal Control with LPV-MPC Based Lateral Control for Autonomous Vehicles［C］∥Proceedings of 2022 European Control Conference. London：IEEE， 2022：518-523.

［13］  GE L H， ZHAO Y， MA F W， et al. Towards Longitudinal and Lateral Coupling Control of Autonomous Vehicles Using Offset Free MPC［J］. Control Engineering Practice， 2022， 121：105074.

［14］  郭景华， 罗禹贡， 李克强. 智能车辆运动控制系统协同设计［J］. 清华大学学报（自然科学版）， 2015， 55（7）：761-768.

GUO Jinghua， LUO Yugong， LI Keqiang. Collaborative Design of a Motion Control System for Intelligent Vehicles［J］. Journal of Tsinghua University（Science and Technology）， 2015， 55（7）：761-768.

［15］  石求军， 李静. 基于扰动观测的客车 ESC 自适应神经网络滑模控制［J］. 中国公路学报， 2021， 34（3）：245-254.

SHI Qiujun， LI Jing. Bus ESC Adaptive Neural Network Sliding Mode Control Based on Disturbance Observation［J］. China Journal of Highway and Transport， 2021， 34（3）：245-254.

［16］  FIORI C， AHN K， RAKHA H A. Power-based Electric Vehicle Energy Consumption Model：Model Development and Validation［J］. Applied Energy， 2016， 168：257-268.

［17］  隗海林， 赖祥翔， 黄朝胜， 等. 基于速度和加速度概率分布的电动汽车能耗计算模型［J］. 吉林大学学报（工学版）， 2014， 44（6）：1591-1595.

KUI Hailin， LAI Xiangxiang， HUANG Chaosheng， et al. EV Calculation Model of Energy Consumption Based on Velocity and Acceleration Distribution［J］. Journal of Jilin University（Engineering and Technology Edition）， 2014， 44（6）：1591-1595.

［18］  杨彩霞. 基于驾驶风格的电动车加速过程优化与控制［D］. 重庆：重庆大学， 2019.

YANG Caixia. Acceleration Process Optimal Control of an Electric Vehicle Based on Driving Styles［D］. Chongqing ：Chongqing University， 2019.

［19］  WANG W， ZHU Q S， WANG Z B， et al. Research on Indoor Positioning Algorithm Based on SAGA-BP Neural Network［J］. IEEE Sensors Journal， 2022， 22（4）：3736-3744.

［20］  GUO N， WANG Z C. A Combined Model Based on Sparrow Search Optimized BP Neural Network and Markov Chain for Precipitation Prediction in Zhengzhou City， China［J］. AQUA Water Infrastructure， Ecosystems and Society， 2022， 71（6）：782-800.

［21］  褚红. 考虑能效优化的四轮驱动电动汽车转矩分配控制［D］.长春：吉林大学， 2020.

CHU Hong.Torque Allocation Control of Four-wheel Drive EVs Considering Energy Efficiency Optimization［D］. Changchun：Jilin University， 2020.

（编辑  王艳丽）

作者简介：

陈志勇，男，1984 年生，副教授。研究方向为车辆动力学与控制、机器人动力学与控制。发表论文20余篇。E-mail：chenzhiyong0203@foxmail.com。