小半径曲线上P75钢轨打磨廓形设计及应用研究

刘永乾 任尊松 侯银庆 吴 潇 王军平

摘要：

以国内某重载铁路R400 m曲线P75钢轨为研究对象，建立了轮轨接触模型和轮径差曲线描述模型，选取代表性车轮踏面和钢轨廓形，采用轮径差曲线逆向求解法优化了轮轨接触区域钢轨廓形，并依据打磨量最小化原则设计得到了曲线钢轨打磨廓形。建立了实测参数下的车辆轨道多体动力学仿真模型，对比分析了实测廓形和设计廓形匹配下的动力学指标。按钢轨廓形设计要求，在该R400 m曲线上实施了钢轨打磨试验和轮轨动力学测试。研究结果表明，优化后轮径差曲线趋于平滑，车辆曲线通过能力得到提高，抗脱轨能力得到保持；轮轨关系得到显著改善、轮轨接触点交叉跳跃和集中问题得到缓解;轮轨横向力减小20%以上，脱轨系数减小16%以上，钢轨法向接触应力减小32%以上，轮轨蠕滑力减小26%以上;实施打磨后，轮轨横向力减小34%以上，脱轨系数减小35%以上，钢轨振动加速度减小35%以上；打磨后3个月轨面疲劳伤损未见明显发展，钢轨使用寿命由前一换轨周期的8个月延长至13.5个月。仿真分析和打磨试验验证了钢轨廓形设计方法在重载铁路小半径曲线的应用效果。

关键词：轮径差曲线；钢轨廓形设计；钢轨打磨；轮轨力；钢轨振动加速度；钢轨磨耗

中图分类号：U216.8

DOI：10.3969/j.issn.1004132X.2024.06.017

开放科学（资源服务）标识码（OSID）：

Research on Design and Applications of Grinding Profiles of P75 Rail on

Sharp Curve

LIU Yongqian1，2  REN Zunsong1  HOU Yinqing2  WU Xiao2  WANG Junping2

1.School of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University，Beijing，100044

2.China Railway Materials Operation and Maintenance Technology Co.，Ltd.，Beijing，100073

Abstract： Taking the P75 rail on R400 m curve of a heavy-haul railway as the research object， the description model of wheel-rail contacts and wheel diameter difference curve was established， and the representative measured wheel treads and rail profiles were selected. The rail profiles in the wheel-rail contact areas were optimized by the reverse solution method of the wheel diameter difference curves， and the grinding profile of the curves was designed according to the principle of minimizing the amounts of grinding. A simulation model of vehicle-track multi-body dynamics with real parameters was established in the multi-body dynamics software， and the dynamic indexes matching with measured and designed profiles were compared and analyzed. The R400 m curve was ground with designed profiles， and the wheel-rail dynamics tests were carried out. The results show that， after optimization， the curves of wheel diameter difference tend to be smoother， the curve passing ability of vehicle is improveds， and the anti-derailment ability is maintained. The wheel-rail relationship is significantly improved matching with the designed profiles， and the cross-jumping and concentration problems at the wheel-rail contact points are alleviated. The lateral wheel-rail force was reduced by more than 20%， the derailment coefficient was reduced by more than 16%， the normal contact stress of the rail is reduced by more than 32%， and the wheel-rail creep force was reduced by more than 26%. After grinding with the designed profile， the lateral wheel-rail force is reduced by more than 34%， the derailment coefficient is reduced by more than 34%， the vibration acceleration of the rail is reduced by more than 35%， the fatigue damage of the rail surface doesnt develop significantly in 3 months， and the service life of the rail is extended from 8 months to 13 months. The application effectiveness of rail profile design method on sharp curve in heavy-haul railway is verified through simulation analysis and field tests.

Key words： wheel diameter difference curve; rail profile design; rail grinding; wheel-rail force; rail vibration acceleration; rail wear

收稿日期：20240106

基金项目：国家自然科学基金重点项目（U2368215）;中国国家铁路集团有限公司科技研究开发项目（N2022G011）

0  引言

钢轨是轨道车辆运行的载体，在长期承受轮轨间交变作用力的情况下极易产生磨耗、裂纹、塑性流动、剥落等病害［1］，而轮轨蠕滑是钢轨病害产生的重要原因之一。针对线路条件进行个性化廓形设计，并通过钢轨打磨实现设计廓形以控制轮轨蠕滑和冲击载荷，是控制和延缓钢轨病害的有效措施之一。郭战伟［2］采用个性化钢轨打磨目标廓形设计方法，对直线和曲线钢轨打磨目标廓形进行了设计。SATO［3］提出了一种充分利用磨耗后的钢轨廓形限制轮轨接触点位移的方法抑制钢轨侧磨发展。GERLICI等［4］以轮轨接触几何参数及静态接触应力为优化目标，提出了基于给定车轮型面的钢轨廓形优化方法。BRANDAU等［5］提出了一种针对轻轨电车的曲线钢轨廓形设计方法。马跃伟等［6］通过建立基于蒙特卡罗方法的轮轨接触概率模型，获得了轮轨接触应力概率分布。崔大宾等［7］提出了一种基于轮轨接触界面法向间隙的钢轨踏面设计方法，对重载线路钢轨廓形进行了优化。MAGEL等［8］提出通过控制轮轨接触点分布范围来获得期望的轮轨几何接触特性的钢轨型面设计方法。王军平［9］提出了一种基于多目标的钢轨廓形优化方法，通过设置多个控制参数进行非对称设计。LIN等［10］、林凤涛等［11］基于非均匀有理B样条理论建立了轮轨型面曲线的三次NURBS描述方法，得到了经济性钢轨打磨型面。XIAO等［12］在考虑岔区轮轨力和车辆过岔横向加速度限值的前提下研究了道岔打磨廓形设计方法。LIU等［13］基于轮轨接触点分布进行了钢轨廓形设计和试验验证。CHOI等［14］从降低曲线钢轨侧磨角度采用基于遗传算法的优化方法对曲线钢轨廓形进行了非对称设计。

目前大多数文献讨论的是在P60钢轨的基础上进行优化设计，但因实际钢轨磨耗严重导致工程应用中实现难度较大，很少能在工程实际中应用设计结果，缺少轮轨力和钢轨磨耗速率等的现场应用验证，因此本文以某重载铁路R400 m曲线P75钢轨为研究对象，以实测车轮踏面和钢轨廓形为基准，采用轮径差曲线逆向求解法优化轮轨接触区域钢轨廓形，在打磨量最小化的前提下设计得到曲线钢轨廓形。通过动力学仿真分析廓形设计结果，并基于钢轨廓形打磨工艺［15-17］实施了钢轨打磨和动力学测试，验证了廓形设计方法的应用效果。该方法是一种通用方法，且本文研究对象（R400 m曲线P75钢轨）通过总重较大、曲线半径较小、试验条件相对恶劣，因此该设计方法适用于通过总重更小、曲线半径更大或铺设P60钢轨的其他线路。

1  代表性车轮踏面和钢轨廓形选取

为使钢轨廓形设计更贴近实际情况，以更好地改善轮轨匹配关系，现场采集了实际车轮踏面和钢轨廓形。该重载铁路主要运行车辆为C80，初始踏面类型为LM，钢轨初始廓形为P75。为减小钢轨廓形设计的轮轨匹配计算工作量，在分析实测踏面和钢轨磨耗的基础上，采用丁军君等［18］提出的方法选出代表性车轮踏面和钢轨廓形作为钢轨廓形设计的输入值。实测踏面和代表性车轮踏面见图1，实测钢轨廓形和代表性钢轨廓形见图2。

2  钢轨廓形设计

轮径差曲线是衡量轮轨动力学性能的主要指标。实测代表性车轮踏面和钢轨廓形匹配的轮径差曲线见图3（图中左侧为靠近曲线上股钢轨方向，下同）。可见轮径差曲线在横移量为-5～8 mm范围内斜率单一，且随横移量增大而减小，不利于车辆轮对曲线通过；在横移量为-7～-5 mm范围内出现了两次明显的阶跃，会产生较大的轮轨冲击。而钢轨廓形设计的目标是使轮径差随轮对横移量增大而单调增大，且分布更加平滑，以减小轮轨冲击，同时保证车辆的曲线通过能力。

考虑到轮径差曲线的唯一性，前提假设条件是轮轨均为刚性，即不考虑轮轨间的弹塑性变形。以轨道中心为坐标原点，此时任意横移量yw下，左右轮轨之间有且仅有一个对应的接触点，分别为：左侧车轮（ywl，zwl）、左侧钢轨（yrl，zrl），右侧车轮（ywr，zwr）、右侧钢轨（yrr，zrr），轮对的侧滚角为φw，因此轮径差ΔR可以表示为

ΔR=zwl－zwr（1）

左侧轮轨接触点可以表示成如下函数：

yrl（yw）=ywl（yw）－zwl（yw）φw（yw）+yw

φw（yw）=ΔR（yw）－（zrl（yw）－zrr（yw））ywr（yw）－ywl（yw）

dzrl（yw）dyrl（yw）=tan（arctandzwl（yw）dywl（yw）+φw（yw））

dzrr（yw）dyrr（yw）=tan（arctandzwr（yw）dywr（yw）+φw（yw））

ΔR=zwl（yw）－zwr（yw）（2）

s.t.  sgn（dzwldywl）=sgn（dzrldyrl）≡1

sgn（d2zrld2yrl）=sgn（d2zrrd2yrr）≡1（3）

若右侧踏面接触点分布已知，则式（2）的11个未知量yw、yrl、zrl、yrr、zrr、ywl、zwl、ywr、zwr、φw、ΔR中，已知的有yw、ywr、zwr和ΔR，又由于ywl、zwl和yrr、zrr中分别只有一个独立变量，则剩余的独立变量数为5，这5个独立变量与5个相互独立的方程构成充要的求解条件。右侧轮轨接触点表达函数同理。

基于轮径差曲线的非对称双侧设计数学问题求解过程如下：

zwl（yw）=fwl（ywl（yw））

zwr（yw）=fwr（ywr（yw））

yrl（yw）=ywl（yw）－zwl（yw）φw（yw）+yw

yrr（yw）=ywr（yw）－zwr（yw）φw（yw）+yw

φw（yw）=ΔR（yw）－（zrl（yw）－zrr（yw））ywr（yw）－ywl（yw）

dzrl（yw）dyrl（yw）=tan（arctandzwl（yw）dywl（yw）+φw（yw））

dzrr（yw）dyrr（yw）=tan（arctandzwr（yw）dywr（yw）+φw（yw））

ΔR（yw）=zwl（yw）－zwr（yw）（4）

通过仿真和数值积分方法进行求解可以得到轮轨接触范围内的钢轨廓形，再将它与实测廓形的非轮轨接触区域进行拼接，可得到完整的曲线钢轨设计廓形。钢轨廓形设计流程见图4。

优化前后轮径差曲线见图5，可见优化后的轮径差曲线在横移量-7～-5 mm范围内阶跃消除，曲线整体趋于平滑，横移量-10～5 mm范围内轮径差随轮对横移量增大而增大；横移量-10～-5 mm范围内轮径差较优化前明显增大，曲线通过能力得到提升；横移量小于-10 mm或大于10 mm范围内轮径差得以维持，抗脱轨性能得到保证。

after optimized

以优化后的轮径差曲线为目标设计得到的曲线钢轨廓形见图6。曲线上股钢轨设计廓形在轨顶中心和外侧区域低于实测廓形，曲线下股钢轨设计廓形在工作边和非工作边低于实测廓形且更加圆顺，较低的部分为需要通过打磨去除的部分，打磨量约0.30～0.45 mm。

曲线钢轨实测廓形和设计廓形与车轮踏面匹配的轮轨接触点分布见图7（图中左轨为上股、右轨为下股）。车轮踏面与实测上股钢轨接触点分布在轨顶非工作边和钢轨侧面，接触位置交叉跳跃，轨顶和轨侧形成了严重的两点接触；下股钢轨接触点主要分布在钢轨工作边内侧，接触点分布较集中。而车轮踏面与设计廓形上股钢轨接触点分布在轨顶中心区域和钢轨侧面，两点接触现象得到缓解；下股钢轨接触点分布在轨顶中心区域和工作边偏内侧区域，上下股钢轨接触位置分布均匀、无交叉跳跃，轮轨接触点集中问题得到有效缓解。

3  仿真结果分析

采用动力学软件仿真分析实测廓形和设计廓形对车辆动力学指标的影响。在SIMPACK软件中建立车辆轨道多刚体动力学模型，其中车辆模型为C80，模型中轮对、轴箱、车辆侧架、摇枕和车体以刚体形式表示，交叉拉杆、弹簧及止挡简化为等效力元，各刚体采用铰接形式连接，钢轨廓形和车轮踏面均为实测数据。轮轨垂向力采用Hertz非线性弹性接触理论进行计算，轮轨蠕滑力/率则采用Fastsim理论进行计算［19-20］，模型见图8。曲线半径为400 m，圆曲线长为300 m，缓和曲线长为100 m，超高为90mm，车辆通过速度为60 km/h，车辆轴重为25 t，车轮踏面和钢轨廓形采用实测数据和优化后的数据，轨道激励采用实测轨道不平顺轨道。该模型已得到文献［21］验证，本文用其

来仿真分析钢轨廓形变化对动力学性能的影响。实测廓形与设计廓形相关动力学指标仿真结果见表1。可知实测廓形和设计廓形上股轮轨横向力均方根值分别为35.22 kN和24.07 kN，下股轮轨横向力均方根值分别为29.87 kN和23.73 kN，设计廓形轮轨横向力较实测廓形轮轨横向力分别减小31.66%和20.56%。实测廓形和设计廓形上股脱轨系数均方根值分别为0.36和0.23，下股脱轨系数均方根值分别为0.30和0.25，设计廓形脱轨系数较实测廓形脱轨系数分别减小33.33%和16.67%。实测廓形和设计廓形上股钢轨法向接触应力均方根值分别为1.28 GPa和0.86 GPa，下股钢轨法向接触应力均方根值分别为1.75 GPa和0.89 GPa，设计廓形钢轨法向接触应力较实测廓形钢轨法向接触应力分别减小32.81%和49.14%。实测廓形和设计廓形上股蠕滑力均方根值分别为25.40 kN和15.41 kN，下股蠕滑力均方根值分别为29.93 kN和22.12 kN，设计廓形蠕滑力较实测廓形蠕滑力分别减小39.33%和26.09%。

4  钢轨打磨试验

以国内某重载铁路为例对前文所述钢轨廓形设计方法及实施效果进行验证。该重载铁路设计时速为80 km/h（R400 m曲线车辆通过速度为60 km/h），铺设P75淬火钢轨，年通过总质量约400×106 t。试验曲线参数同第3节仿真计算模型，钢轨存在的主要问题为侧磨速率较大（上道后8个月左右达到16 mm轻伤下道标准）、轨面裂纹和剥离掉块等严重疲劳伤损，严重影响钢轨使用寿命。

试验曲线钢轨于2021年4月20日上道、2022年6月中旬下道，期间对其进行了4次钢轨打磨。每次打磨前按实测钢轨廓形设计钢轨打磨廓形，按个性化钢轨廓形打磨实施流程［22］进行打磨方案设计、实施和验收。采用96头钢轨打磨车实施打磨，其打磨量约0.1 mm、打磨精度约0.02 mm，可每次保证打磨后钢轨廓形与设计廓形偏差满足标准［23］要求，单次钢轨打磨量约0.3～0.4 mm。历次打磨前后钢轨廓形见图9。

对试验曲线进行了为期13.5个月的跟踪观测，共采集14次钢轨廓形，得到上股钢轨侧磨测量曲线如图10所示。可知在经历4次钢轨打磨

后，该曲线上股钢轨在上道13.5个月后侧磨量达到16.6 mm，使用寿命较前一换轨周期的8个月延长了68.75%，表明按设计廓形打磨可有效降低上股钢轨侧磨速率。

打磨前和打磨后3个月试验曲线中位置轨面疲劳伤损情况见图11。该曲线钢轨上道后2个月时轨面存在严重斜裂纹和剥离掉块，最大掉块深度超过1 mm。按设计廓形打磨3个月后同一位置轨面仅存在轻微斜裂纹，表明按设计廓形打磨可有效控制轨面疲劳伤损发展。

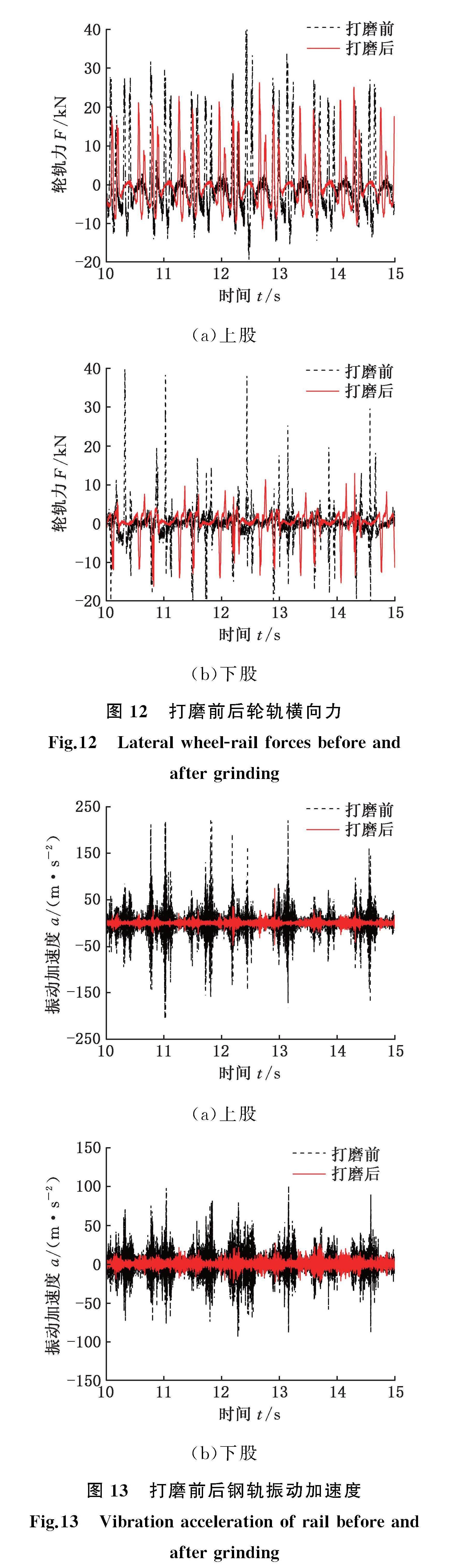
对试验曲线进行打磨前后动力学测试，得到打磨前后轮轨横向力见图12。

由图12可知，打磨前后上股轮轨横向力最大值分别为39.96 kN和26.07 kN，打磨后上股轮轨横向力减小34.76%；打磨前后下股轮轨横向力最大值分别为39.7 kN和15.53 kN，打磨后下股轮轨横向力减小60.88%。经计算，打磨前后上股实测脱轨系数分别为0.34和0.22，打磨后上股实测脱轨系数减小35.29%；打磨前后下股实测脱轨系数分别为0.36和0.21，打磨后下股实测脱轨系数减小41.67%。实测数据与第3节仿真分析数据基本吻合，导致差异的可能因素包括车辆实际运行速度、测试车辆载重或车轮踏面磨耗差异等。

打磨前后钢轨振动加速度曲线见图13。可知打磨前后上股钢轨振动加速度最大值分别为220.65 m/s2和74.61 m/s2，打磨后上股钢轨振动加速度减小66.17%；打磨前后下股钢轨振动加速

度最大值分别为100.51 m/s2和26.93 m/s2，打磨后下股钢轨振动加速度减小73.01%。

5  结论

（1）实测车轮踏面和钢轨廓形匹配的轮径差曲线在横移量为-5～8 mm范围内斜率单一，且随横移量增大而减小，不利于车辆轮对曲线通过；在横移量为-7～-5 mm范围内出现了两次明显阶跃，会产生较大的轮轨冲击。优化后的轮径差曲线更加平滑，轮径差随横移量增大而增大，曲线通过能力得到提升，抗脱轨性能得到保持。同时轮轨接触点交叉跳跃和集中问题得到缓解。

（2）动力学仿真分析结果表明，在车轮踏面等其他因素不变的前提下，钢轨设计廓形相较于实测廓形的轮轨横向力、脱轨系数、钢轨法向接触应力和轮轨蠕滑力等动力学指标均显著减小，与轮径差优化结果吻合。

（3）钢轨打磨试验结果表明，打磨后轮轨横向力和钢轨振动加速度幅值均大幅减小，打磨后3个月轨面疲劳伤损未见明显发展，钢轨使用寿命由前一换轨周期的8个月延长至13.5个月。

（4）仿真分析和打磨试验验证了钢轨廓形设计方法在重载铁路R400 m曲线上的应用效果，该方法同样适用于通过总重更小、曲线半径更大或铺设P60钢轨的其他线路。

参考文献：

［1］  XU Lei， ZHAI Wanming， GAO Jianmin. Global Sensitivity Analysis for Vehicle-track Interactions：Special Attention on Track Irregularities［J］. Journal of Computational and Nonlinear Dynamics， 2018， 13（3）：031007.

［2］  郭战伟.普速铁路钢轨打磨对轮轨接触关系的影响［J］.中国铁道科学，2020，41（6）：109-116.

GUO Zhanwei. Influence of Rail Grinding on Wheel-Rail Contact Relationship in General Speed Railway［J］. China Railway Science， 2020， 41（6）：109-116.

［3］  SATO Y. Design of Rail Head Profiles with Full Use of Grinding［J］. Wear， 1991， 144（1/2）：363-372.

［4］  GERLICI J， LACK T. Railway Wheel and Rail Head Profiles Development Based on the Geometric Characteristics Shapes［J］.Wear， 2011， 271（1）：246-258.

［5］  BRANDAU  J， POLL G. Wear Reduction in Light Rail Systems through Asymmetrical Railhead Profiles［J］. Tribology， 2002， 40：305-316.

［6］  马跃伟，任明法，胡广辉，等. 高速铁路钢轨预打磨型面优化分析［J］. 机械工程学报，2012，48（8）：90-97.

MA Yuewei， REN Mingfa， HU Guanghui， et al. Optimal Analysis on Rail Pre-grinding Profile in High-speed Railway［J］. Journal of Mechanical Engineering， 2012， 48（8）：90-97.

［7］  崔大宾，李立，金学松，等. 铁路钢轨打磨目标型面研究［J］.工程力学，2011，28（4）：178-184.

CUI Dabin， LI Li， JIN Xuesong， et al. Study on Rail Goal Profile by Grinding［J］. Engineering Mechanics， 2011， 28（4）：178-184.

［8］  MAGEL E， RONEY M， KALOUSEK J， et al. The Blending of Theory and Practice in Modern Rail Grinding［J］. Fatigue & Fracture of Engineering Materials & Structures， 2010， 26（10）：921-929.

［9］  王军平. 基于廓形打磨的小半径曲线钢轨磨耗控制方法研究［J］. 铁道学报，2021，43（1）：128-134.

WANG Junping.Research on Rail Wear Control Method Based on Profile Grinding for Sharp Curve Rail［J］. Journal of Railways， 2021，43（1）：128-134.

［10］  LIN Fengtao， ZHOU Shuang， DONG Xiaoqing， et al. Design Method of LM Thin Flange Wheel Profile Based on NURBS［J］. Vehicle System Dynamics， 2021， 59（1）：17-32.

［11］  林凤涛， 胡伟豪. 磨耗钢轨经济性打磨型面研究［J］. 铁道科学与工程学报， 2020， 17（10）：2493-2502.

LIN Fengtao， HU Weihao. Study on the Economical Grinding Surface of Wear Rail［J］. Journal of Railway Science and Engineering， 2020， 17（10）：2493-2502.

［12］  XIAO Qian， YANG Yihang， CHANG Chao， et al. Monitoring and Evaluation of High-speed Railway Turnout Grinding Effect Based on Field Test and Simulation［J］. Applied Sciences， 2023， 13：9177.

［13］  LIU Xingyu， SHI Jin， WANG Yingjie. A Design Method for Rail Profiles Based on the Distribution of Contact Points［J］. Structural and Multidisciplinary Optimization， 2023， 66（226）：1-18.

［14］  CHOI H Y， H LEE D， SONG C Y， et al. Optimization of Rail Profile to Reduce Wear on Curved Track［J］. International Journal of Precision Engineering and Manufacturing， 2013（4）：619-625.

［15］  王军平，沈钢，毛鑫，等. 钢轨廓形打磨关键环节及智能化实现［J］. 同济大学学报（自然科学版）， 2021， 49（5）：680-686.

WANG Junping， SHEN Gang， MAO Xin， et al. Key Links and Intelligent Realization of Rail Profile Grinding［J］. Journal of Tongji University（Natural Science）， 2021， 49（5）：680-686.

［16］  刘永乾，任尊松，吴潇，等. 钢轨打磨对小半径曲线钢轨滚动接触疲劳的影响研究［J］.铁道学报， 2023， 45（8）：110-117.

LIU Yongqian， REN Zunsong， WU Xiao， et al. Influence of Rail Grinding on Rolling Contact Fatigue of Rail on Small-radius Curve［J］. Railway Engineering， 2023， 45（8）：187-194.

［17］  李志和. 重载铁路钢轨非对称型面打磨策略研究［D］. 南昌：华东交通大学， 2020.

LI Zhihe. Research on Asymmetrical Profile Grinding Strategy for Heavy-haul Railway［D］. Nanchang：East China Jiaotong University， 2020.

［18］  丁军君，吴朋朋，王军平，等.基于轮轨关系的钢轨打磨代表廓形计算方法研究［J］.铁道学报， 2019， 41（7）：135-140.

DING Junjun， WU Pengpeng， WANG Junping， et al. Study on Algorithm of Representative Profile for Rail Grinding Based on Wheel-rail Relationship［J］. Journal of Railways， 2019， 41（7）：135-140.

［19］  宋志坤，侯银庆，胡晓依，等. 柔性轮轨下轮轨波磨综合作用的振动特性研究［J］. 铁道学报， 2018，40（11）：33-40.

SONG Zhikun， HOU Yinqing， HU Xiaoyi， et al. Research on Vibration Characteristics of Wheel-rail Corrugation under Flexible Wheel and Rail［J］. Journal of Railways， 2018，40（11）：33-40.

［20］  吴潇，丁军君，戚壮，等.曲线钢轨磨耗演变预测及对车辆动力学影响研究［J］.铁道科学与工程学报， 2020， 17（2）：460-468.

WU Xiao， DING Junjun， QI Zhuang， et al. Study on the Prediction of Curve Rail Wear Evolution and Its Influence on Vehicle Dynamics［J］. Journal of Railway Science and Engineering， 2020， 17（2）：460-468.

［21］  吴潇. 客货共线铁路曲线钢轨磨耗预测研究［D］.成都：西南交通大学， 2021.

WU Xiao.Prediction of Rail Wear in Curve of Mixed Passenger and Freight Railway［D］. Chengdu：South West Jiaotong University， 2021.

［22］  王军平，单连琨，丁军君，等. 个性化钢轨廓形打磨方法分析［J］.铁道建筑，2015，55（11）：131-133.

WANG Junping， SHAN Liankun， DING Junjun， et al. Analysis of Personalized Rail Profile Grinding Method［J］. Railway Engineering，2015，55（11）：131-133.

［23］  中国国家铁路集团有限公司. 普速铁路钢轨打磨验收标准 TJ/GW170—2021［S］. 北京：中国国家铁路集团有限公司， 2021.

China State Railway Group Co.， Ltd. Acceptance Standard for Rail Grinding of Ordinary Speed Railway TJ/GW170-2021［S］. Beijing：China State Railway Group Co.， Ltd.， 2021.

（编辑  王艳丽）

作者简介：

刘永乾，男，1990年生，博士研究生。研究方向为钢轨打磨与轮轨关系。E-mail：liuyqcrm@qq.com。

任尊松（通信作者），男，1969年生，教授、博士研究生导师。研究方向为车辆结构可靠性与动力学。E-mail：zsren@bitu.edu.cn。