基于小样本数据驱动的弹壳打凹平底成形工艺参数优化决策方法

梁强 李雄 王海洋 王伟任 徐永航 刘新 杜彦斌

摘要：

针对某外贸款弹壳在调试生产中加工质量差和模具寿命短的问题，提出一种基于小样本数据驱动的弹壳打凹平底成形工艺参数多目标优化与决策方法。首先，利用中心复合试验法设计试验，将各试验方案代入有限元模型中进行数值模拟，以仿真结果为基础采用随机森林算法建立弹壳打凹平底成形工艺参数与打凹下冲头最大等效应力、平底上冲头最大等效应力和平底成形后弹壳内圆角的多目标优化模型。其次，应用改进多目标灰狼优化算法对多目标优化模型进行寻优并获得非劣解集，采用主客观综合熵权优劣解距离法评价决策出最优工艺参数组合。最后，采用该优化工艺参数组合进行数值模拟和工艺试验，结果显示，模拟结果与工艺试验结果吻合，弹壳底部内圆角充填饱满，模具使用寿命得到提高。

关键词：弹壳；小样本驱动；改进多目标灰狼优化算法；打凹平底成形

中图分类号：TG319

DOI：10.3969/j.issn.1004132X.2024.06.014

开放科学（资源服务）标识码（OSID）：

Optimization Decision Method for Cartridge Case Indenting-heading Process

Parameters Driven by Small Sample Data

LIANG Qiang1  LI Xiong2  WANG Haiyang3  WANG Weiren2  XU Yonghang1

LIU Xin2  DU Yanbin1

1.School of Mechanical Engineering，Chongqing Technology and Business University，Chongqing，400067

2.Chongqing Changjiang Electrical Appliances Industries Group Co.，Ltd.，Chongqing，401336

3.The Third Military Representative Office in Chongqing，Chongqing，400000

Abstract： Aiming at the problems of low quality and short die life during the production commissioning， an optimization decision method for cartridge case indenting-heading process parameters driven by small sample was proposed. Firstly， the central composite experimental method was used to design experiments， and each experimental scheme was incorporated into the finite element model for numerical simulation. Taking the maximum effective stress of indenting ejector， the maximum effective stress of heading punch and inner fillet at the bottom of the cartridge case as the optimization goals， random forest algorithm was combined to construct the multi-objective optimization model of processing parameters in indenting-heading processes of cartridge cases based on the simulation results. Secondly， the improved multi-objective grey wolf algorithm was applied to optimize the multi-objective optimization model and obtain a pareto solution. The optimal process parameter combination was evaluated and determined using the comprehensive entropy weight-TOPSIS method. Finally， the numerical simulation and processing experiments were carried out with the combination of optimal process parameters. The results show that the simulation results are consistent with the processing experiments， and the inner fillets at the bottom of the cartridge cases are filled fully， and the service life of the die is improved.

Key words： cartridge case; small sample drive; improved multi-objective grey wolf optimization algorithm; indenting-heading

收稿日期：20230920

基金项目：重庆市自然科学基金（CSTB2022NSCQ-MSX0473）；重庆市高校创新研究群体项目（CXQT21024）；制造装备机构设计与控制重庆市重点实验室开放课题（KFJJ2019078）；重庆工商大学研究生创新型科研项目（YJSCXX2023-211-54）

0  引言

枪弹由弹头、弹壳、底火和发射药构成，弹壳是承装发射药的容器、装配弹头和底火的部件，保证其在大批量生产过程中的高效、优质和稳定是当下枪弹数字与智能化设计与加工的主要研究方向之一［1-3］。

目前弹壳的生产工艺常采用经验法进行类比设计，在面对新型高集成加工设备和高柔性动态生产环境时，往往需要长时间占线调整和调试。随着“数智化”技术升级，部分研究开始采用有限元模拟仿真耦合数据驱动方法构建弹壳成形过程质量控制模型。廖仕军等［4］基于运动弹平底成形数值模拟结果构建弹壳平底成形工艺参数优化数学模型。王玉松［5］采用BP神经网络和遗传算法相结合的方法优化了铝合金弹壳挤盂凸模结构参数，降低了弹壳成形后的剪切应力。邹宇等［6］以提高弹壳成形质量为优化目标，基于数值模拟仿真与正交试验设计，对弹壳拉深工艺的3个结构参数进行了优化。胡开元等［7］将响应面法和数值模拟方法相结合，优化了弹壳拉深成形工艺参数。

基于有限元模拟仿真耦合数据驱动构建弹壳成形质量控制模型时，其模型精度与样本量有直接关系。大样本容量需要进行大量的有限元模拟仿真，这样会导致出现设计时间过长、工作量偏大的问题。而在调试生产过程中面对的特定问题，小样本数据驱动方法只需要少量数据即可以进行模型训练并保证一定的预测精度，降低了机器学习对“大数据”的依赖［8］，可以快速实现调试过程特定问题的优化与决策。

目前，试验设计是一种减少试验次数并合理、高效收集数据的有效手段。张在房等［9-10］针对大型贮箱箱底充液拉深成形起皱和破裂的问题，采用拉丁超立方抽样方法进行试验设计，构建了成形工艺参数与质量指标之间的代理模型，并通过多目标寻优确定了最优工艺参数。任振宝等［11］针对动力电池壳拉深成形时的起皱、破裂、壁厚不均匀等问题，基于正交试验设计和数值模拟仿真方法，提出了一种基于熵权的综合评价法对电池壳拉深成形工艺参数进行多目标优化来提高成形质量。YAGHOUBI等［12］采用基于正交试验设计的神经网络和蜜蜂算法对2024铝合金板拉深成形工艺参数进行优化。CHEBBAH等［13］采用基于拉丁超立方抽样试验设计的代理模型与遗传算法对管材液压成形工艺参数进行了优化。RAMANJANEYULU等［14］结合正交试验设计与灰色关联分析对黄铜壳体拉深成形工艺参数进行了优化。

本文以某外贸款枪弹弹壳为研究对象，将中心复合试验设计与随机森林（random forest， RF）算法相结合，构建弹壳底部打凹平底成形工艺参数多目标优化模型；以提高弹壳成形质量和避免模具早期失效为目的，采用改进多目标灰狼算法（multi-objective grey wolf algorithm， MOGWO）在可行域内寻优，并采用主客观综合熵权优劣解距离法（technique for order preference by similarity to an ideal solution， TOPSIS）决策出最优工艺参数组合，并将该参数组合应用于工艺试验进行验证。

1  弹壳打凹-平底成形工艺分析

某外贸款弹壳的成形流程简图见图1a，弹壳材料为H68黄铜。在调试生产过程中，平底上冲头的模具使用寿命短，平均使用寿命约为500个/件，低于其他型号弹壳平底上冲头的平均模具使用寿命（30 000个/件），平底上冲头主要失效形式为断裂，模具材料为Cr12MoV。图1b所示为断裂的平底上冲头及卡在弹壳底部的模具凸起部分。对平底后的弹壳进行尺寸检验，检验结果显示弹壳底火室内圆角超差，如图1c所示。

为了分析当前技术参数下打凹平底成形过程中金属流动规律、弹壳形状尺寸变化及模具应力分布情况，应用有限元软件构建弹壳打凹平底成形二维有限元模型并进行数值模拟仿真，相关模拟参数见表1。

有限元分析结果如图2所示。打凹下冲头的模具应力分析结果见图2a，它在凸起过渡圆角处的最大等效应力为1990 MPa，未超过实际使用模具材料Cr12MoV钢的抗压屈服强度范围2500～3000 MPa［15］。平底上冲头的模具应力分析结果如图2b所示，它在圆角处的最大等效应力达到2790 MPa，已超过使用强度范围的下限，因此在实际使用时非常容易出现断裂的情况，这与实际情况基本吻合。图2c所示为平底成形后弹壳底火室内圆角与模具的充填情况，内圆角与平底上冲头没有完全贴合，虽然该圆角尺寸0.50.10 mm设有公差，但下料质量的波动、各工序模具磨损和模具安装误差等均可能导致该内圆角尺寸超差，进而使产品质量不合格，因此，需针对弹壳打凹平底成形工艺参数进行再设计和再优化，以提高产品质量和模具使用寿命。

2  基于中心复合试验设计的打凹平底成形多目标优化模型

基于小样本试验的弹壳打凹平底成形优化决策方法流程如图3所示。本方法以弹壳打凹平底成形工艺参数为优化变量，以提高模具使用寿命和产品质量为优化目标。

2.1  优化变量和优化目标

平底成形为弹壳底部的一道整形工序，即通过将打凹成形的弹壳通过局部冷镦挤整形至最终设计尺寸，因此，平底成形的上冲头、下冲头和凹模尺寸均无法改变，但平底成形后连皮厚度h（图4）可以在一定尺寸范围内优化调整。打凹成形是平底成形的预成形工序，其主要作用是将拉深成形的弹壳底部金属进行预分配，若打凹成形金属体积分配不合理，将导致平底成形后弹壳底火室缺料而充不满亦或料太多而出现纵向毛刺，因此，选择打凹成形下冲头的凸起高度L、圆角R和锥角δ进行优化，如图4所示。

根据第一节分析，为了提高产品质量和模具使用寿命，本文选择打凹下冲头最大等效应力σA、平底上冲头最大等效应力σB和弹壳底火室内圆角与平底上冲头的最大间距C（如图2c所示）作为优化目标。

2.2  中心复合试验设计

中心复合试验设计是评估优化目标和优化变量之间非线性关系的一种试验设计方法［16］。本文试验以弹壳打凹平底成形的4个工艺参数作为优化变量，每个变量在原设计参数附近各取5个水平，各变量的水平取值见表2。确定因素与水平后，应用Design-expert软件进行中心复合试验设计，并根据具体试验安排分别依次进行模具设计、数值模拟和结果测量，最终试验结果见表3。

2.3  多目标优化模型构建

随机森林（RF）是一种基于样本数据拟合多个输入参数与输出结果的模型［17］，该模型由多棵分类树或回归决策树集合而成。相比传统的拟合算法，随机森林模型构建时具有样本随机性和特征随机性，因此它不需要大量的试验数据，并且存在计算速度快、准确度高的优点。本文采用RF模型构建弹壳打凹平底成形工艺参数优化模型，具体的建立流程如图5所示，步骤如下：

（1）数据处理。RF模型不需要进行数据归一化处理，只需划分训练集和测试集。从30组样本随机抽选出25个样本作为训练集，其余5个样本组成测试集，训练集与测试集样本量比例为5∶1。

（2）RF模型回归效果及预测精度仍然会受到决策树的数量n、决策树最大特征数m和叶节点的最小样本数量s这三个超参数的影响，因此，在构建基于RF的弹壳打凹平底成形工艺参数多目标优化模型时，本文采用网格搜索法对超参数n、m和s进行优化，以提高模型预测精度。超参数的取值范围为：n∈［1， 500］，m∈［1， 4］，s∈［1， 50］。

（3）计算适应度值。以测试集的均方根误差作为适应度值，计算每个网格点的适应度值并进行比较，输出适应度值最小的超参数nbest、mbest、sbest，即通过网格搜索法获得RF最优超参数。

（4）模型评价。通过最优的三个参数nbest、mbest、sbest建立RF模型，为了评价构建模型的预测精度及泛化能力，采用相关性系数（correlation coefficient）R、均方根误差值（root mean square error， RMSE）σRMSE和平均相对误差（mean absolute error， MAE）σMAE进行评价，计算公式如下：

R=∑Ni=1（xi-）（ri-）∑Ni=1（xi-）2∑Ni=1（ri-）2（1）

σRMSE=1N∑Ni=1（xi－ri）2（2）

σMAE=1N∑Ni=1|xi－ri|（3）

式中，xi为真实试验值；ri为模型预测值；、为真实试验值和模型预测值的均值；N为数据集样本数。

（5）输出预测值。应用RF模型对弹壳打凹平底成形的打凹下冲头最大等效应力σA、平底上冲头最大等效应力σB和弹壳底火室内圆角与平底上冲头的最大间距C进行预测。

RF模型预测值的线性回归结果如图6所示，3个优化目标无论是训练集还是测试集的预测值均贴近最佳拟合线（R=1），3个优化目标的相关系数R均大于0.9，说明预测值与试验值线性关系紧密、预测值接近试验值。与此同时，为了对比不同模型在预测精度及拟合程度的表现，分别采用BP神经网络（back propagation neural network，BPNN）、极限学习机（extreme learning machine， ELM）模型和支持向量回归（support vector regression， SVR）模型对同一试验数据进行建模，结果见表4。其中，σRMSE和σMAE值越小，表示模型误差越小，4个模型中，预测精度和拟合程度从大到小的排序为：RF，BPNN，SVR，ELM。综上，RF模型具有较强的预测能力与泛化性，可以为后续弹壳打凹平底成形工艺参数优化求解提供可靠的预测模型支持。

将打凹下冲头最大等效应力σA、平底上冲头最大等效应力σB和弹壳底火室内圆角与平底上冲头的最大间距C定义为3个优化目标，其中减小打凹下冲头最大等效应力σA和平底上冲头最大等效应力σB可以有效提升模具使用寿命，减小弹壳底火室内圆角与平底上冲头的最大间距C可以提高弹壳成形质量。弹壳打凹平底成形工艺参数多目标优化模型为

f（h，R，L，δ）=min（σA，σB，C）

s.t.  1.4 mm≤h≤1.8 mm

0.8 mm≤R≤1.6 mm

2.9 mm≤L≤3.3 mm

5.0°≤δ≤7.0°（4）

3  基于改进MOGWO算法和综合熵权-TOPSIS法的多目标优化与决策

3.1  算法流程图

根据第二节构建的多目标优化模型，利用改进MOGWO算法进行多目标优化并获得最优帕累托（Pareto）解集，通过综合熵权-TOPSIS对Pareto解集中各个解进行排序以寻找最优方案，最终获取弹壳打凹平底成形最佳工艺参数组合。结合MOGWO和综合熵权-TOPSIS的优化、决策方法实现流程见图7。

3.2  改进MOGWO算法多目标优化

MOGWO算法是2016年由MIRHALILI等［18］通过模拟野生狼群的社会等级和集群捕食策略设计的一种元启发式算法。算法将要优化的参数看作灰狼种群，狼群分为4个等级，即：α→β→γ→ω，α等级最高，ω等级最低。每只灰狼的位置为G=（G1，G2，…，GM），其中M为空间维度，寻优过程中每支灰狼按照下式寻找猎物目标：

D=EGp（t）－G（t）

G（t+1）=Gp（t）－AD

A=2ar1－aF

E=2r2（5）

式中，D为距离矢量；t为迭代次数；Gp（t）为猎物位置；A、E为系数向量；r1、r2为［0，1］之间的随机向量；a为收敛因子；F为元素全为1的向量。

在原MOGWO算法中，收敛因子a直接影响前期全局搜索能力和后期局部搜索能力及算法收敛速度和鲁棒性。原MOGWO算法中a在迭代过程中从2线性递减至0，容易导致前期全局搜索能力不足而陷入局部最优、后期搜索步长过大而精度不足。目前关于收敛因子的改进方法主要为从线性递减改为非线性递减。根据采用的函数类型大致可以分为指数函数型［19-20］：

a=2－2I－1（It/T－1）（6）

有理函数型［21］ ：

a=1－（t/T）21－μ（t/T）2（7）

三角函数型［22］：

a=2cos（π2tT）（8）

和Sigmoid函数型［23-24］：

a=2－21+exp［－30（t/T－0.5）］（9）

式中，T为最大迭代次数；I为控制系数，计算时I取100；μ为调节指数，计算时μ取0.1。

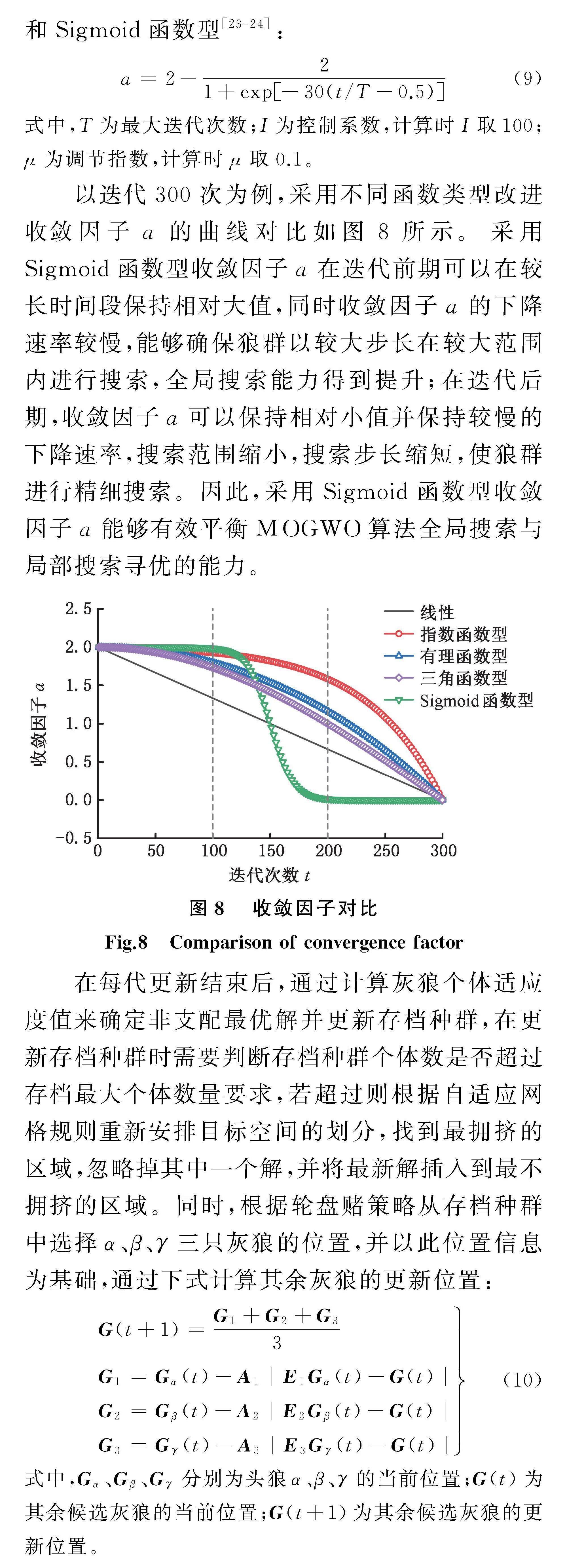
以迭代300次为例，采用不同函数类型改进收敛因子a的曲线对比如图8所示。采用Sigmoid函数型收敛因子a在迭代前期可以在较长时间段保持相对大值，同时收敛因子a的下降速率较慢，能够确保狼群以较大步长在较大范围内进行搜索，全局搜索能力得到提升；在迭代后期，收敛因子a可以保持相对小值并保持较慢的下降速率，搜索范围缩小，搜索步长缩短，使狼群进行精细搜索。因此，采用Sigmoid函数型收敛因子a能够有效平衡MOGWO算法全局搜索与局部搜索寻优的能力。

在每代更新结束后，通过计算灰狼个体适应度值来确定非支配最优解并更新存档种群，在更新存档种群时需要判断存档种群个体数是否超过存档最大个体数量要求，若超过则根据自适应网格规则重新安排目标空间的划分，找到最拥挤的区域，忽略掉其中一个解，并将最新解插入到最不拥挤的区域。同时，根据轮盘赌策略从存档种群中选择α、β、γ三只灰狼的位置，并以此位置信息为基础，通过下式计算其余灰狼的更新位置：

G（t+1）=G1+G2+G33

G1=Gα（t）－A1|E1Gα（t）－G（t）|

G2=Gβ（t）－A2|E2Gβ（t）－G（t）|

G3=Gγ（t）－A3|E3Gγ（t）－G（t）|

（10）

式中，Gα、Gβ、Gγ分别为头狼α、β、γ的当前位置；G（t）为其余候选灰狼的当前位置；G（t+1）为其余候选灰狼的更新位置。

迭代至最大迭代次数后，存档种群中保存的解即为一组最优Pareto解集。

原MOGWO算法在位置更新时容易陷入局部最优解，为此本文在原位置更新算式中增加服从柯西（Cauchy）分布数的柯西变异算子以产生较大的变异步长，发挥柯西变异算子的大扰动优势，提升算法的全局搜索能力。改进后灰狼位置更新计算式为

G（t+1）=G（t+1）（1+|a|2Cauchy（0，1））（11）

基于改进MOGWO算法对弹壳打凹平底成形工艺参数进行多目标优化，种群规模为100，迭代次数为100，存档数为100，优化结果如图9所示，其中Pareto前沿解集中包含100组解。

3.3  综合熵权-TOPSIS综合评价方法

经MOGWO算法优化后得到一组由100个解组成的Pareto解集，如何针对现有指标选择合适的评价方法对该解集中各个解作出有效的评价是决策的关键。本文采用TOPSIS［25］和主客观综合熵权法构建综合评价决策体系，将经MOGWO算法寻优得到的Pareto解集代入到综合评价指标中进行计算与决策。具体步骤如下：

（1）建立决策矩阵和标准矩阵。经MOGWO算法得到的Pareto解集组成决策矩阵P=［pij］uSymboltB@v，共u组待决策工艺参数组合，u=100，v个评价指标，v=3。TOPSIS法使用距离尺度来度量样本之间的差距，因此首先需要对不同属性的各指标进行同向化处理。本文研究的3个目标均希望越小越好，因此为极小型指标，采用下式进行同向化处理：

qij=max pj-pijmax  pj-min pj（12）

其中，Q=［qij］uSymboltB@v为正向化处理得到的矩阵。

其次，对正向化数据进行标准化，标准化的目的是消除不同指标量纲的影响，各指标进行标准化，即每一列元素都除以当前列向量的范数，由此得到标准化处理后的标准矩阵S=［sij］uSymboltB@v，其中

sij=qij/∑ui=1q2ij（13）

（2）主客观综合熵权法计算权值。主观赋权法具有较强的主观随意性，客观性较差；客观赋权法未能考虑决策者对不同属性的重视程度，忽略了主观决策者的判断和不易量化的影响，差异性较大，因此本文采用主客观综合熵权法计算衡量3个目标的权重值。分别计算各指标的信息熵值Hj和客观熵权λj：

Hj=－1ln u∑ui=1（sijln sij）（14）

λj=（1－Hj）/∑vj=1（1－Hj）（15）

并由下式计算得出综合熵权wj：

wj=τjλj/（∑vj=1τjλj）（16）

其中，主观熵权τj由10位工厂工艺处人员根据3个指标的重要程度讨论后得出，各指标的综合熵权见表5。

（3）计算欧氏距离并输出综合评分。s+由S中每列元素的最大值构成，s-由S中每列元素的最小值构成。分别由下式计算矩阵S中各个解与s+、s-之间的距离D+i和D－i：

D+i=∑vj=1wj（s+j－sij）2（17）

D-i=∑vj=1wj（s-j－sij）2（18）

并由下式计算各个解的综合评分ci ：

ci=D－iD+i+D－i（19）

从而得出各个解的排序。ci值越大，说明该解越优，排序越高。排名前10组的解如表6所示。

3.4  多目标优化方法的性能对比分析

为了证明改进MOGWO算法在弹壳打凹平底成形工艺参数优化方面的优势，分别选择多目标遗传算法（NSGA-Ⅱ）、多目标粒子群算法（MOPSO）和原MOGWO算法进行对比。NSGA-Ⅱ算法设置为：种群规模100，迭代次数100，交叉比例0.8，变异概率0.05。MOPSO算法设置为：种群规模100，迭代次数100，惯性权重0.4，学习因子2，自适应网格等分量20。原MOGWO算法的设置参照3.2节。为了评估四种算法的收敛性和多样性，选择超体积（hypervolume， HV）VH和反转世代距离（inverted generational distance， IGD）DIG这2个性能指标进行评估［26-27］，其计算公式分别为

VH=ζ（∪|K|i=1Vi）（20）

DIG（Pa，Pa）=∑x∈Paminy∈Pad（x，y）|Pa|（21）

式中，ζ为Lebesgue测度，用来测量体积；|K|为非支配解集的数目；Vi为参考点与解集中第i个解构成的超体积；Pa为算法得到的解集；P*a为一组均匀分布的参考点；d（x， y）为P*a集中的点x到解集Pa中的点y之间的欧氏距离；|Pa|为解集的数目。

表7所示为4种算法对打凹平底成形多目标优化模型独立运算10次所求的的HV和IGD性能指标的计算结果，其中VH值越大，DIG值越小，说明算法的综合性能越好。由表7可看出，改进MOGWO算法的HV和IGD性能指标的均值均为最优，说明改进MOGWO算法具有较好的收敛性和多样性。同时改进MOGWO算法只有IGD方差略大于NSGA-Ⅱ算法方差，其HV指标的方差均小于其他算法的方差，说明改进MOGWO算法的鲁棒性较好。

4种算法在20代和100代收敛情况如图10所示，在迭代至20次时，MOPSO和原MOGWO算法尚未形成Pareto前沿解，而改进MOGWO和NSGA-Ⅱ算法已经收敛并形成较完整的Pareto前沿解。由表8可知，改进MOGWO算法的最优值与NSGA-Ⅱ算法相当，但改进MOGWO算法Pareto解集中所有解的平均值小于NSGA-Ⅱ算法所有解的平均值。综上可得，改进MOGWO算法的收敛速度及优化效果较好。

4  试验验证

以表6中排名前5的解为基础，结合实际模具加工精度及实际调试过程中的安装精度，将上述优化求得的工艺参数进行适当圆整，其结果为：h=1.57±0.01 mm，R=0.95±0.05 mm，L=3.27±0.02 mm，δ=5.85±0.05°。

首先，采用该优化结果进行有限元模拟，结果如图11所示。打凹下冲头的模具应力分析结果如图11a所示，它在凸起过渡圆角处的最大等效应力为1890 MPa，模拟结果与模型预测结果1915.360 MPa的误差为1.34%；平底上冲头的模具应力分析结果如图11b所示，它在圆角处的最大等效应力为2080 MPa，

最大等效应力较原工艺下降25.45%，与模型预测结果2157.739 MPa误差为3.74%；图11c所示为平底成形后弹壳底火室内圆角与模具的充填情况，内圆角与平底上冲头几乎完全贴合。由数值模拟结果可得，打凹下冲头与平底上冲头最大等效应力均在模具材料Cr12MoV的强度范围内，可以避免早期失效的情况，同时弹壳充填效果较原工艺参数得到有效提升。

其次，采用该优化工艺参数组合制作相应的工模具并进行工艺试验，现场试验生产该款弹壳约2万粒，期间未出现模具断裂情况。每生产500粒抽选1粒进行尺寸检验，弹壳底火室内圆角均未超差，试验生产的弹壳如图12a所示。弹壳打凹和平底成形数值模拟结果与工艺试验结果的对比情况，如图12b所示。由图12可看出，工艺试验与数值模拟结果吻合，采用优化后的工艺参数组合可以获得满足设计要求的弹壳。将试制产品按照正常工艺加工至成品，进行功能测试，经产量加倍测试验证，

满足验收要求，可以说明优化方案对后续加工工序无影响。

5  结论

针对调试生产过程中弹壳加工质量差和模具寿命短的问题，提出一种基于小样本数据驱动的弹壳打凹平底成形工艺参数多目标优化与决策方法。相关结论如下：

（1）针对小样本数据，以中心复合试验进行试验设计，分别以随机森林（RF）、BP神经网络（BPNN）、支持向量回归（SVR）、极限学习机（ELM）四种算法构建多目标优化模型并评估其预测能力，结果显示RF算法具有较强的预测能力与泛化性，可以为后续弹壳打凹平底成形工艺参数优化求解提供可靠的预测模型支持。

（2）分别应用多目标粒子群算法（MOPSO）、多目标遗传算法（NSGA-Ⅱ）、多目标灰狼算法（MOGWO）和改进MOGWO算法对多目标优化模型进行寻优，改进MOGWO算法在收敛速度、鲁棒性和优化效果上优于其他算法，表明其具备较强的全局搜索能力和局部搜索能力。

（3）本文采用主客观综合熵权-TOPSIS法对寻优得到的Pareto解集进行评价与决策，通过计算排序后得到了最优工艺参数组合。采用优化工艺参数组合进行数值模拟和工艺试验，结果显示，模拟结果与工艺试验结果吻合，弹壳底部内圆角充填饱满，模具使用寿命得到提高。

参考文献：

［1］  刘新， 郭睦基， 李登虎， 等. 弹壳拉深成形工艺分析及模具设计［J］. 锻压技术， 2022， 47（12）：81-86.

LIU Xin， GUO Muji， LI Denghu， et al. Process Analysis and Die Design on Cartridge Deep Drawing［J］. Forging & Stamping Technology， 2022， 47（12）：81-86.

［2］  MANABE K I， SOEDA K， SHIBATA A. Effects ofVariable Punch Speed and Blank Holder Force in Warm Superplastic Deep Drawing Process［J］. Metals， 2021; 11（3）：493.

［3］  ZEIN H L E， ABDRABOU M， ELSHERBINY M， et al. Effect of Die Design Parameters on Thinning of Sheet Metal in the Deep Drawing Process［J］. American Journal of Mechanical Engineering， 2013， 1（2）：20-29.

［4］  廖仕军， 吕刚， 薛松， 等. 弹壳底部平底成形工艺优化［J］. 兵器装备工程学报， 2020， 41（11）：182-185.

LIAO Shijun， LYU Gang， XUE Song， et al. Study on Flattening Shaping Process-optimized for Campaign Bullet［J］. Journal of Ordnance Equipment Engineering， 2020， 41（11）：182-185.

［5］  王玉松. 7050铝合金弹壳成形工艺优化及热处理工艺的研究［D］. 重庆：重庆大学， 2015.

WANG Yusong. Research on the Heat Treatment Process and Optimization of Forming Process of 7050 Aluminum Alloy Cartridge［D］. Chongqing：Chongqing University， 2015.

［6］  邹宇， 王名川， 陈才， 等. 基于有限元方法的弹壳拉深成形工艺结构参数研究［J］. 锻压技术， 2022， 47（11）：123-129.

ZOU Yu， WANG Mingchuan， CHEN Cai， et al. Research on Structural Parameters of Deep Drawing Process for Cartridge Case Based on FEM［J］. Forging & Stamping Technology， 2022， 47（11）：123-129.

［7］  胡开元， 王雷刚. 基于响应面法与灰狼优化算法的壳体拉深成形模具优化设计［J］. 锻压技术， 2022， 47（6）：244-250.

HU Kaiyuan， WANG Leigang. Optimization Design on Shell Deep Drawing Die Based on Response Surface Methodology and Grey Wolf Optimization Algorithm［J］. Forging & Stamping Technology， 2022， 47（6）：244-250.

［8］  LI H， WEN G， JIA X， et al. Augmenting Features by Relative Transformation for Small Data［J］. Knowledge-based System， 2021， 225（7）：107121.

［9］  张在房， 徐冯， 孙习武. 火箭贮箱箱底充液拉深成形工艺的多目标优化［J］. 机械工程学报， 2022， 58（5）：78-86.

ZHANG Zaifang， XU Feng， SUN Xiwu. Multi-objective Optimization of Hydroforming Process of Rocket Tank Bottom［J］. Journal of Mechanical Engineering， 2022，58（5）：78-86.

［10］  徐冯， 张在房， 孙习武. 贮箱箱底充液拉深成形工艺参数的多目标优化［J］. 计量与测试技术， 2021， 48（6）：53-57.

XU Feng， ZHANG Zaifang， SUN Xiwu. Multi-objective Optimization of Hydroforming Technological Parameters for Tank Bottom［J］. Metrology & Measurement Technique， 2021， 48（6）：53-57.

［11］  任振宝， 曹春平. 基于熵权综合评价法的动力电池壳首道次拉深成形参数优化［J］. 中国机械工程， 2022， 33（13）：1622-1628.

REN Zhenbao， CAO Chunping. Optimization of First Deep Drawing Process Parameters for Power Battery Shells Based on Entropy Weight Comprehensive Evaluation Method［J］. China Mechanical Engineering， 2022， 33（13）：1622-1628.

［12］  YAGHOUBI S， FERESHTEH-SANIEE F. Optimization of the Geometrical Parameters for Elevated Temperature Hydro-mechanical Deep Drawing Process of 2024 Aluminum Alloy［J］. Proceedings of the Institution of Mechanical Engineers Part E：Journal of Process Mechanical Engineering， 2021， 235（2）：151-161.

［13］  CHEBBAH M S， LEBAAL N. Tube Hydroforming Optimization Using a Surrogate Modeling Approach and Genetic Algorithm［J］. Mechanics of Advanced Materials & Structures， 2018， 27（6）：515-524.

［14］  RAMANJANEYULU P， VENKATARAMAIAH P， REDDY K D. Multi Parameter Optimization of Deep Drawing for Cylindrical Cup Formation on Brass Sheets Using Grey Relational Analysis［J］. Materials Today：Proceedings， 2019， 18（7）：2772-2778.

［15］  张俊喜， 陈百明， 郭小汝， 等. Cr12MoV钢凸模失效分析［J］. 模具工业， 2016， 42（10）：67-71.

ZHANG Junxi， CHEN Baiming， GUO Xiaoru， et al. Failure Analysis on Punch with Cr12MoV Steel［J］. Die & Mould Industry， 2016， 42（10）：67-71.

［16］  曹永娟， 冯亮亮， 毛瑞， 等. 轴向磁场永磁记忆电机多目标分层优化设计［J］. 中国电机工程学报， 2021， 41（6）：1983-1991.

CAO Yongjuan， FENG Liangliang， MAO Rui， et al. Multi-objective Stratified Optimization Design of Axial-flux Permanent Magnet Memory Motor［J］. Proceedings of the CSEE， 2021， 41（6）：1983-1991.

［17］  梁旭东， 王炜， 赵凯， 等. 随机森林回归分析在激光熔覆形貌预测中的应用［J］. 中国有色金属学报， 2020， 30（7）：1644-1652.

LIANG Xudong， WANG Wei， ZHAO Kai， et al. Application of Random Forest Regression Analysis in Trace Geometry Prediction of Laser Cladding［J］. 2020， 30（7）：1644-1652.

［18］  MIRHALILI S， SAREMI S， MIRHALILI S M， et al.Multi-objective Grey Wolf Optimizer：a Novel Algorithm for Multi-criterion Optimization［J］. Expert Systems with Application， 2015， 47（4）， 106-119.

［19］  易茜， 柳淳， 李聪波， 等. 基于小样本数据驱动的滚齿工艺参数低碳优化决策方法［J］. 中国机械工程， 2022， 33（13）：1604-1612.

YI Qian， LIU Chun， LI Congbo， et al. A Low Carbon Optimization Decision Method for Gear Hobbing Process Parameters Driven by Small Sample Data［J］. China Mechanical Engineering， 2022， 33（13）：1604-1612.

［20］  崔博， 王坤， 王佳俊， 等. 基于改进MOGWO的复杂交通隧洞车辆定位布设优化［J］. 水利水电技术， 2022， 53（7）：105-115.

CUI Bo， WANG Kun， WANG Jiajun， et al. Improved MOGWO-based Optimization of Vehicle Positioning Deployment in Complicated Traffic Tunnel［J］. Water Resources and Hydropower Engineering， 2022， 53（7）：105-115.

［21］  薛阳， 燕宇铖， 贾巍， 等. 基于改进灰狼算法优化长短期记忆网络的光伏功率预测［J］. 太阳能学报， 2023， 44（7）：207-213.

XUE Yang， YAN Yucheng， JIA Wei， et al. Photovoltaic Power Prediction Model Based on IGWO-LSTM［J］. Acta Energiae Solaris Sinica， 2023， 44（7）：207-213.

［22］  何祖杰， 吴新烨， 刘中华. 基于改进灰狼算法优化支持向量机的短期交通流预测［J］. 厦门大学学报：自然科学版， 2022， 61（2）：288-297.

HE Zujie， WU Xinye， LIU Zhonghua. Optimized SVM Model for Short-term Traffic Flow Prediction Based on Improved Gray Wolf Optimizer［J］. Journal of Xiamen University：Natural Science， 2022，61（2）：288-297.

［23］  谭美芳， 匡锐， 张清勇， 等. 基于改进灰狼算法优化LSTM的断面交通流预测［J］. 武汉理工大学学报， 2023， 45（5）：132-139.

TAN Meifang， KUANG Rui， ZHANG Qingyong， et al. LSTM for Cross-sectional Traffic Flow Prediction Based on Improved Grey Wolf Optimizer Algorithm［J］. Journal of Wuhan University of Technology， 2023， 45（5）：132-139.

［24］  侯钰哲， 李舜酩， 龚思琪， 等. 滚动轴承故障特征选择的Filter与改进灰狼优化混合算法［J］. 计算机集成制造系统， 2023， 29（5）：1452-1461.

HOU Yuzhe， LI Shunming， GONG Siqi， et al. Hybrid Algorithm of Filter and Improved Gray Wolf Optimization for Fault Feature Selection of Rolling Bearing［J］. Computer Integrated Manufacturing Systems， 2023，29（5）：1452-1461.

［25］  蒋荣超， 刘大维， 王登峰. 基于熵权TOPSIS方法的整车动力学性能多目标优化［J］. 机械工程学报， 2018， 54（2）：150-158.

JIANG Rongchao， LIU Dawei， WANG Dengfeng. Multi-objective Optimization of Vehicle Dynamics Performance Based on Entropy Weighted TOPSIS Method［J］. Journal of Mechanical Engineering， 2018， 54（2）：150-158.

［26］  ZHANG Q， LI H. MOEA/D：a Multi Objective Evolutionary Algorithm Based on Decomposition［J］. IEEE Transactions on Evolutionary Computation， 2007， 11（6）：712-731.

［27］  RUSSO L M S， FRANCISCO A P. Quick Hypervolume［J］. IEEE Transactions on Evolutionary Computation， 2014， 18（4）：481-502.

（编辑  王艳丽）

作者简介：

梁  强，男，1988年生，副教授。研究方向为精密塑性成形工艺及优化、模具制造及再制造。E-mail：2017015@ctbu.edu.cn。