接触物系的速度、加速度关联性探讨

赖永强

摘 要：文章以接触物系的速度、加速度关联性探讨为例，提倡 “一题多解、多题类比”的习题讲评模式，立足于学生思维能力的培养，引导其通过知识的分析、归纳、迁移，进行深度学习.

关键词：接触物系；深度学习；关联速度；关联加速度

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）15-0079-03

深度学习指向核心知识的掌握、关键技能的培养，是学科核心素养达成的有效途径.高中物理课堂不仅在科学探究课中关注学生深度学习，在习题讲评课中也同样应该渗透深度学习的意识.

1 理论依据

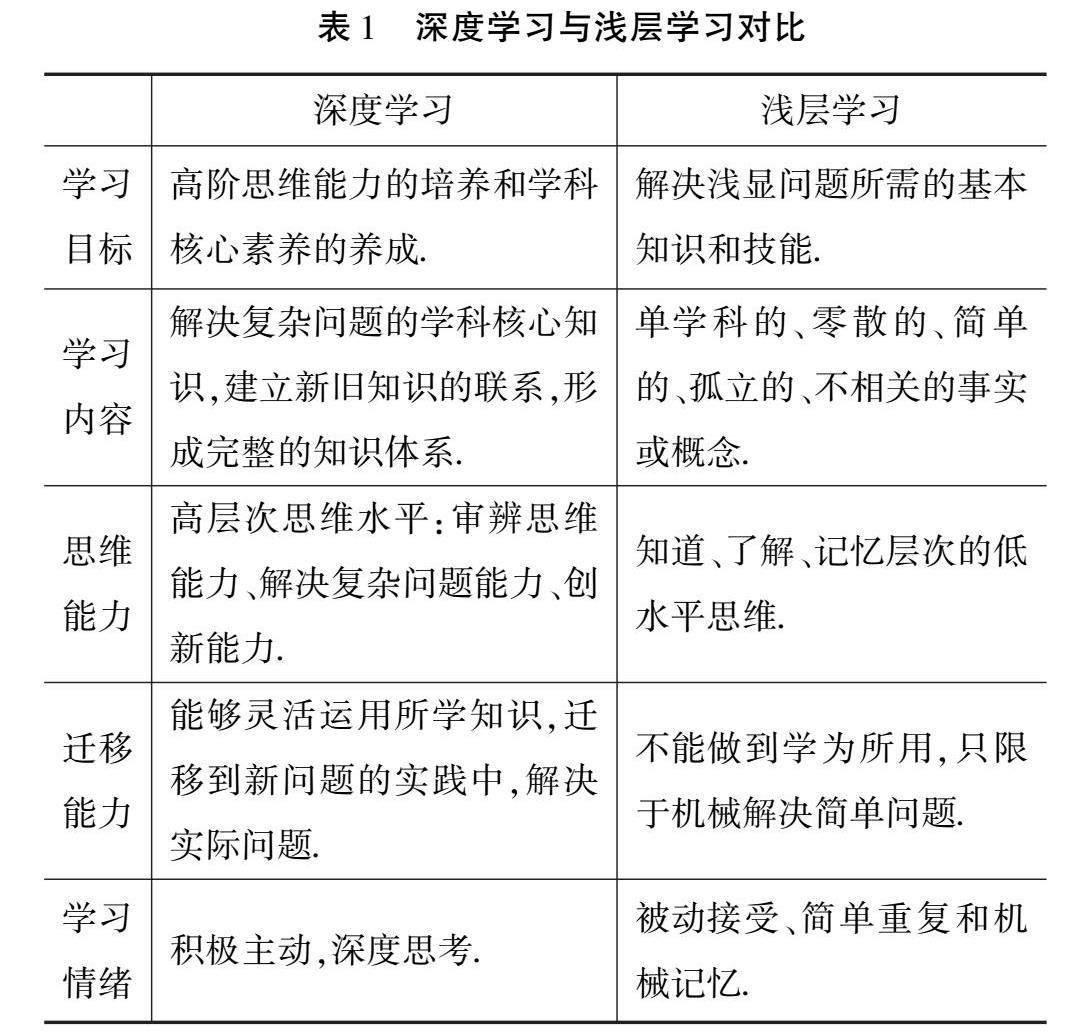
深度学习的概念国内外还没有统一的界定.深度学习是针对机械记忆、被动接受的浅层学习方式而提出的，下表[1]是深度学习与浅层学习的简单对比.

从表中看出，深度学习以培养高阶思维为目标，注重知识整合，反对将知识零散、孤立地简单处理，强调主动学习、批判接受新知识，着眼于知识的迁移和问题的解决.学生要深度学习，反过来我们老师要“深度教学”.郭元祥教授论证了从深度学习走向深度教学的必然性，认为深度教学不是无限增加知识难度和知识量，而是克服对知识的表层学习、机械训练的局限性，基于知识的内在结构，通过对知识完整处理，引导学生从符号学习走向学科素养的学习[2].

2 问题背景

对于有约束条件下的物系相关性，高中阶段仅要求掌握绳（杆）约束情况下两端的速度关联，而对于接触物系接触点的速度、加速度的关联性问题高中阶段基本不作要求，但此类关联问题在历年的高校自主招生、物理竞赛考试中却屡见不鲜.下面分别以接触面为平面、圆弧面为例，分别探讨它们接触点的速度、加速度的关联性.

3 典例分析

3.1 接触面为平面的物系相关性探讨

3.1.1 速度关联性探讨

例1 如图1，某时刻三角形斜面A的速度为v0，加速度为a0，已知θ，求竖直杆B上升的速度大小vB.

解法1 利用速度关联法，培养学生矢量分解意识.

由于刚体不可形变，根据A、B相互接触不分离的约束性可知，沿接触面的法线方向，两接触物A、B必须有相同的分速度.所以可以将斜面A、杆B的速度沿斜面方向和垂直斜面方向分解，如图2.则有：

v0sinθ=vBcosθ

∴vB=v0tanθ

这种方法的关键点是：（1）正确找到合速度，即物体的实际速度；（2）正确分解速度，即沿接触面法线方向和切线方向分解速度；（3）根据法线方向分速度相等列式.

解法2 利用数学求导法，培养学生运用数学知识解决物理问题的能力.

根据物系间的约束关系，利用数学方法进行推导，如图3，斜面向右运动位移大小和杆向上运动位移大小满足关系：

h=xtanθ

dhdt=ddt（x tanθ

∴vB=v0tanθ

此方法通过寻找相互接触的两物体之间的位移几何关系，从而建立函数关系式，再利用数学求导来寻找两接触物系的速度关联，这种方法让学生更深刻理解物理基本概念（速度的定义），同时运用数学知识解决物理问题的能力也是物理高考五大能力要求之一.学会这种方法，能够解决更多更复杂的物理问题，真正提高学生分析问题、解决问题的能力.

3.1.2 加速度关联性探讨

针对上面例1，求此时刻杆的加速度与斜面加速度关系.

利用数学求导的方法进行求解：

∵vB=v0tanθ

∴dvBdt=ddt（v0tanθ

∴aB=a0tanθ（或vBcosθ=v0sinθ

以上分析可知，沿接触面垂直的方向上具有相同的加速度，即对于接触面为平面的接触系，不仅速度具有关联性，两物体的加速度也具有关联性.

3.2 接触面为圆弧面的物系相关性探讨

3.2.1 速度关联性探讨

例2 如图5，某时刻半球面A的速度为v0，加速为a0，已知θ，求竖直杆B上升的速度大小vB.

由于杆和球面始终接触，根据接触面的速度关联，沿法线方向速度相等，则：

v0sinθ=vBcosθ

∴vB=v0tanθ

当然，本例题也可以类似例1，采用数学求导方法、相对运动法、功率相等法来找到两者速度关系，在此就不再赘述了.

3.2.2 加速度关联性探讨

针对上面例2，求此时竖直杆的加速度aB与a0关系.

不少同学认为杆与球面相接处，加速度具有关联性，即沿着法线方向具有相同的分加速度，所以得到两者关系： a0sinθ=aBcosθ

∴aB=a0tanθ

这种计算方法对不对呢？如果接触面是平面的情况下，杆的加速度求解直接从速度求解方法中迁移过来，但对于接触面是曲面的情况，杆的加速度求解能不能简单地从速度求解方法中迁移过来呢？两者的加速度是否具有关联性？下面通过数学、物理两个不同角度来求解这两者间加速度的关系.

解法1 数学方法，对速度进行求导.

根据杆与球面的速度关联有：

vB=v0tanθ

∴dvBdt=ddt（v0tanθ

∴aB=a0tanθ+v0ddt（tanθ

=a0tanθ+v0ddθ（tanθ）dθdt

=a0tanθ+v01cosθ2dθdt

式中dθdt大小等于接触点P绕圆心O逆时针转动的角速度大小ω，根据角速度与线速度关系有ω=vτR，线速度vτ是以半球面为参考系，接触点P相对于圆心O的速度，如图5.

图5 速度关联

dθdt=ω=vτR=v0Rcosθ

因为θ在减小，所以dθdt为负值，

即dθdt=-v0Rcosθ ， 所以：

aB=a0tanθ-v20Rcosθ3

解法2 根据接触物系加速度关联性求解

以半球面为参考系，接触点P相对于圆心O做圆周运动，线速度大小为：vτ=v0cosθ，该速度产生向心加速度大小为：a向=v2τR=v20Rcosθ2 ，方向指向圆心O.

如图6，根据接触物系接触点法向加速度分量相等可以列式：

aBcosθ=a0sinθ-a向

∴aB=a0tanθ-v20Rcosθ3

图6 加速度关联

由此看出，对于接触面是曲面的情况，接触系的加速度关联并不能简单地将两个加速度沿法向、切向方向分解，认为沿法向加速度相等得到两者的关系，这里还必须考虑曲线运动时产生向心加速度，所以在列加速度关联式时必须结合向心加速度将等式进行“修正”.

4 结束语

两道看起来相似的题目，其实不大一样，不少学生在学习的过程中，没有深入理解接触面的物系关联原理，对知识、解题方法生搬硬套，盲目“迁移”，就很容易出错.通过两道例题的深入剖析，不仅能够澄清修正自己原有的错误认识，也能对接触面的物系关联有更清晰的理解.在解题过程中提倡“一题多解，多题类比”，综合利用数学、物理方法进行深入分析，学生体会到物理方法解题方便简洁的同时，也感受到数学知识解决物理问题带来的美妙.

高中物理有很强的逻辑性和系统性，在物理习题教学过程中很有必要通过“一题多解、多题类比”教学方式引导学生深度学习、深度思考，将原有知识方法进行归纳、迁移、提升，并不断提出问题、思考问题、解决问题.这是一个知识、经验与心智融合的过程，是一个不断提升科学思维能力的过程，在培养学生深度学习能力上起到事半功倍的效果.

参考文献：

［1］曾志旺.物理教学中促进“深度学习”的教学设计[J].物理通报，2017（5）：70-73.

[2] 郭元祥.论深度教学：源起、基础与理念[J].教育研究与实验，2017（3）： 1-11.

［责任编辑：李 璟］