例谈建立空间直角坐标系的原则和方法

赵志强

摘 要：本文先介绍建立空间直角坐标系的原则和方法，然后举例说明在不规则图形中建立坐标系的方法.

关键词：立体几何；空间直角坐标系；建立坐标系；方法

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）15-0061-03

从课本的例题中看出， 建立空间直角坐标系解决问题的例题背景基本上是正方体、长方体或底面是直角三角形的直三棱柱.因为这些几何体十分容易建系，解决问题水到渠成，但有些例题没有建立空间直角坐标系，而是选取恰当的基底解决问题.课本没有建立空间直角坐标系求解是基于以下三个原因：①有的空间直角坐标系不易建立；

②若建立了恰当的空间直角坐标系，点的坐标不易写出；

③运算较麻烦.

但是立体几何问题中的点、线、面、体千差万别，丰富多彩，有的用综合法或“基底法” 比较难以解决问题，而用“坐标法”比较快捷.而且现在的新课标高考中立体几何试题大多数用 “坐标法”都易于解决[1].那么怎样建立恰当的空间直角坐标系呢？ 其实它与平面直角坐标系的建立方式相似，难的是竖轴z怎样与x轴，y轴与原点形成标配.

1 建立空间直角坐标系的三大原则

原则一：特殊点为空间坐标系的原点O.

原则二：过O且互相垂直的两条特殊直线为x轴与y轴 （或x轴、z轴或y轴、z轴），由此确定第三条轴的产生.

原则三：有利运算 （最适当的空间直角坐标系）.

有的几何体随着思考者的主观性和角度不同，建立的空间坐标系也不同，从而运算过程大多不同，但结论都是一致的，恰当的空间直角坐标系会让运算简捷，起到事半功倍的效果[2].

2 常见的几种模型及建立方法一般情况下，在立体图形中有下面的几种模型.

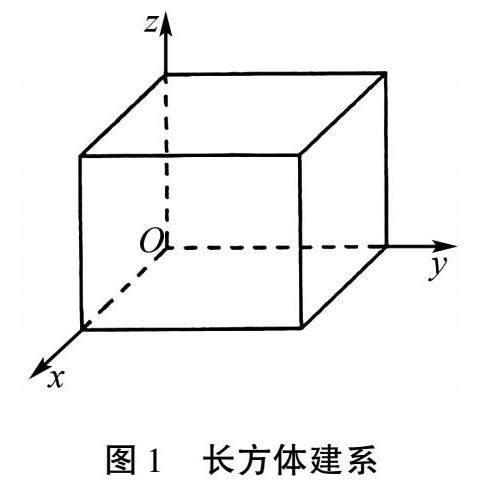
模型1 正方体（长方体）型

这种模型是最常见的模型， 教材的例题多是这种情况，一般建立如图1所示的空间直角坐标系.

模型2 直棱柱型

直棱柱型一般常见的是直三棱柱或直四棱柱或直六棱柱， 出现频率最高的是直三棱柱， 其次是直四棱柱.

（1）直三棱柱的底面是直角三角形， 可视为长方体的一半.通常以底面直角三角形的顶点为坐标原点，建立如图2所示的空间直角坐标系.

（2）直三棱柱的底面是正三角形 （即正三棱柱）， 通常以底面一边的中点为原点， 建立如图3所示的空间直角坐标系.

（3）直三棱柱的底面是一般三角形时， 可根据具体情况选择原点，x轴，y轴， 常常以一边与该边上的高分别为x轴与y轴， 垂足为原点.特别地， 当底面是等腰三角形时， 取底边的中点为原点， 底边上的高所在的直线为x轴 （或y轴）， 如图4.

模型3 斜棱柱型

常见的斜棱柱的底面三角形一般为特殊三角形，且某个侧面与底面垂直或侧棱与底面成已知角度， 常寻找垂直元素为坐标轴建立空间直角坐标系.

例1[3] 如图5，已知斜三棱柱ABC-A1B1C1的棱长均为2，平面ACC1A1⊥平面ABC， 侧棱与底面成60°的角.

（1）求AB1与BC1所成角的余弦值；

（2）求BC1与平面ABB1A1所成角的正弦值；

（3）在线段AB1与线段BC1上是否分别存在点P，Q， 使PQ∥平面ACC1A1， 若存在， 求出P，Q的位置， 若不存在， 请说明理由.

解 设AC的中点为D.连接A1C，A1D，DB，由于平面A1ACC1⊥平面ABC， 且侧棱与底面所成的角为60°， 三棱柱ABC-A1B1C1的棱长均为 2 ，所以△ABC和△A1AC为正三角形.故以D为原点，DB，DC，DA1所在的直线分别为x轴，y轴，z轴， 建立如图6所示的空间直角坐标系， 则D（0，0，0），A（0，-1，0），B（3，0，0），C（0，1，0），A1（0，0，3），B1（3，1，3），C1（0，2，3）.

（1）AB1=（3，2，3），BC1=（-3，2，3），cos〈AB1，BC1〉=AB1·BC1AB1BC1=410×10=25，即AB1与BC1所成角的余弦值为25.

（2） 因为AB=（3，1，0），AB1=（3，2，3），

设平面ABB1A1的法向量为n=（x，y，z），

则n·AB=0，n·AB1=0， 所以3x+y=0，3x+2y+3z=0，

取x=1， 则y=-3，z=1， 所以平面ABB1A1的一个法向量n=（1，-3，1）.

设BC1与平面ABB1A1所成角为θ， 则

sinθ=cos〈BC1，n〉=BC1·nBC1|n|

=|-3-23+3|10×5=65，

所以BC1与平面ABB1A1所成角的正弦值为65.

（3）假设存在满足条件的点P，Q， 且设AP=λAB1，BQ=μBC1，λ，μ∈（0，1）.所以DP=DA+

λAB1=（0，-1，0）+λ（3，2，3）=（3λ，-1+2λ，

3λ），DQ=DB+μBC1=（3，0，0）+μ（-3，2，3）=（3-3μ，2μ，3μ）， 所以

PQ=DQ-DP=（3-3μ-3λ，1+2μ-2λ，3μ-3λ），

而平面ACC1A1的一个法向量为DB=（3，0，0），

所以PQ·DB=0，即μ+λ=1，

即当AP=C1Q时，PQ∥平面ACC1A1.

特别地， 当λ=μ=12时，P，Q分别是AB1与BC1的中点.

模型4 棱锥型

棱锥型跟棱柱型的空间直角坐标系的建立方法基本一致.但正棱锥可取底面的中心为坐标原点.（特别是正四棱锥）.

模型5 圆柱型

圆柱形的空间直角坐标系的建立大多数以如图7所示的方法建立.

模型6 其他几何体型

其他几何体千姿百态，但一般给出的几何体的点、线、面及其关系含有很多特殊元素与特定的关系，可以结合平面几何的相关知识与空间直角坐标系的常规方法建立恰当的空间直角坐标系.

例2[4] 如图8，平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将ΔABD沿BD折起，使得平面ABD⊥平面BDC（如图9），设点E，F分别是AC，AD的中点.

（1）求证：DC⊥平面ABC；

（2）求钝二面角B-EF-A的余弦值.

解 （1）略.

（2）以B为原点，BD为x轴正向，BA为z轴正向建立空间直角坐标系如图10.设CD=a，则BD=AB=2a，BC=3a，AD=22a，易知B0，0，0，A0，0，2a，D2a，0，0，Fa，0，a，E3a4，3a4，a，CD=a2，-3a2，0，BF=a，0，a，BE=34a，34a，a，AC=32a，32a，-2a.

设平面ACD的法向量为n1=x1，y1，z1，则有CD·n1=0，AC·n1=0，即a2x1-32ay1=0，3a2x1+32ay1-2az1=0，取n1=（3，1，3）.

设平面BEF的法向量为n2=x2，y2，z2，则有BE·n2=0，BF·n2=0，即3a4x2+34ay2+az2=0，ax2+az2=0，取n2=（-3，-1，3）.

∴cos＜m，n>=-1-1/3+1

21/3·21/3=17，

又二面角为钝二面角，所以所求二面角B-EF-A的余弦值为-17.

3 结束语

新教材比较重视向量方法在立体几何中的应用，而新高考中的立体几何大题，都可以通过建立空间直角坐标系，用向量方法来解决.可以这么说，建立空间直角坐标系是解决立体几何大题的通法，所以，除了规则的几何体外，我们要掌握在不规则几何体中建立空间直角坐标系的方法.

参考文献：

［1］唐明超，于雷.一类立体几何试题的模式化解法分析：以2019年全国卷Ⅰ试题为例[J].教学考试，2019（38）：58-62.

[2] 安国钗，张正华.巧建坐标系妙用解析法[J].理科考试研究，2019，26（24）：19-23.

[3] 李鸿昌.点在面内的多视角证明与高观点审视：一道2020年立体几何高考题引发的探究[J].数理化解题研究，2023（22）：101-104.

[4] 李鸿昌.高考题的高数探源与初等解法[M].合肥：中国科学技术大学出版社，2022.

［责任编辑：李 璟］