浅谈“双减”视域下初中数学分层作业的甄选

丁虹 胡勇

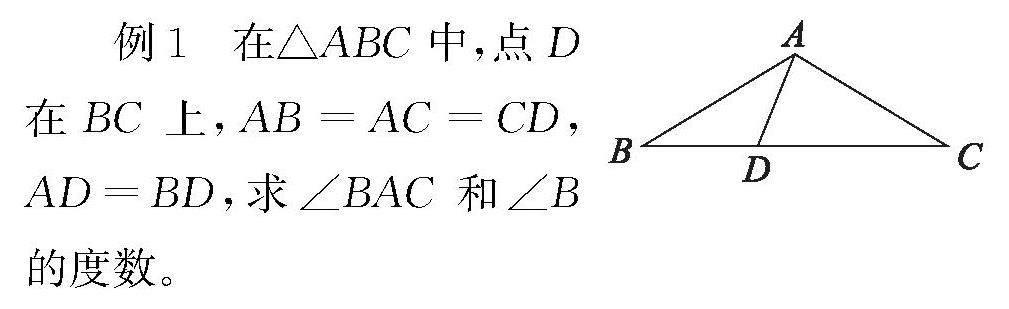
本文系合肥市教育信息技术研究课题“‘双減背景下基于初中数学智慧作业的分层性实践研究”的成果，课题编号为HDJ22070。

摘要：“双减”政策对义务教育阶段学生的作业负担进行政策上的指导。但减负不减质，初中数学作业设计要充分利用分层作业，做到题目少而精，在甄选、创新题型上下功夫，重视作业评价与时俱进，从而提升学生的数学核心素养。

关键词：“双减”  初中数学  分层作业

《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》指出，要“健全作业管理机制”“分类明确作业总量”“提高作业设计质量”。为实现“立德树人”根本任务，“布置分层、弹性和个性化作业”的关键环节在于作业的甄选设计。本文将深入研究“双减”视域下初中数学分层作业的甄选，以期为教育实践提供可行的建议和探索路径。

一、“双减”政策对初中数学分层作业的影响

第一，针对学生个体差异分层教学，满足不同学习需求。根据学生的能力和水平进行作业的选择和分配，这有助于培养学生的自主学习和合作学习能力，提高他们的数学核心素养。在分层作业的甄选过程中，教师可以结合学生的兴趣和爱好来规划作业内容，以激发学生的学习动力和积极性。

第二，“双减”政策要求初中数学分层作业与教学目标、课程内容相结合。数学分层作业设计应充分考虑教学目标、课程内容，才能确保其能够促进学生学习。

第三，减负政策的实施使得学生的学习负担减轻，让学生有更多的时间和精力进行深度学习，这就要求分层作业的设计必须更加精确、合理。

此外，教师还需要借助多媒体教学和在线学习平台，提供更加灵活、多样的教学方式。

二、初中数学分层作业的甄选原则

（一）整体性原则

2022年版的《义务教育数学课程标准》提出了“设计体现结构化特征的课程内容”的课程理念，要求学生能“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系”。这给初中数学分层作业设计提出了整体性的要求。

1．本学习领域内设计

根据新课程标准，义务教育阶段的数学课程内容分为四大学习领域，整体性首先体现在本学习领域内的知识内容。例如，在设计“轴对称图形”第一课时的作业时，可以设计有关旋转对称图形、四边形和圆等平面几何图形知识的题目，促使学生在完成作业时回顾整个图形与几何的相关知识，体现了整体性原则。

2．跨学习领域间联系

整体性也体现在两个或两个以上具有内在联系的学习领域之间。如例1，引导学生将几何与代数两大领域结合，用代数方法求解三角形中角的度数问题。学生通过独立思考、合作交流，逐步感悟数学思想。

例1  在△ABC中，点D在BC上，AB=AC=CD，AD=BD，求∠BAC和∠B的度数。

3．跨学科领域间合作

学科融合呈现作业设计的原创精神与改革理念。例2展示了数学实践性作业与美术学科的结合，将轴对称图形知识应用在美术作品的设计上，这种跨学科的作业提高了学生的综合素质。

例2  用剪纸或者画画的方式亲手制作一件轴对称美术作品。

（二）多元化原则

1.作业内容多元化

设计分层作业可以让作业内容多元化。分层作业一般包括基础性作业、拓展性作业和提优性作业。学生在完成作业时可根据自己的能力进行选择，学生积极性得到保护，学习兴趣也得到激发。如轴对称图形第二课时的作业，可设计：基础题6道，可融入生活元素；拓展题1道，形式为解答题，以考查平面直角坐标系的应用为主；提优题1道，以折纸为主要题境。这样每个学生都可以找到适合自己的作业，数学能力都能得到训练。

作业内容多元化能够促进学生各方面能力的发展，获得数学学习的成就感，增强自信心，丰富多彩的作业内容可以提升学生学习数学的兴趣。

2.作业评价多元化

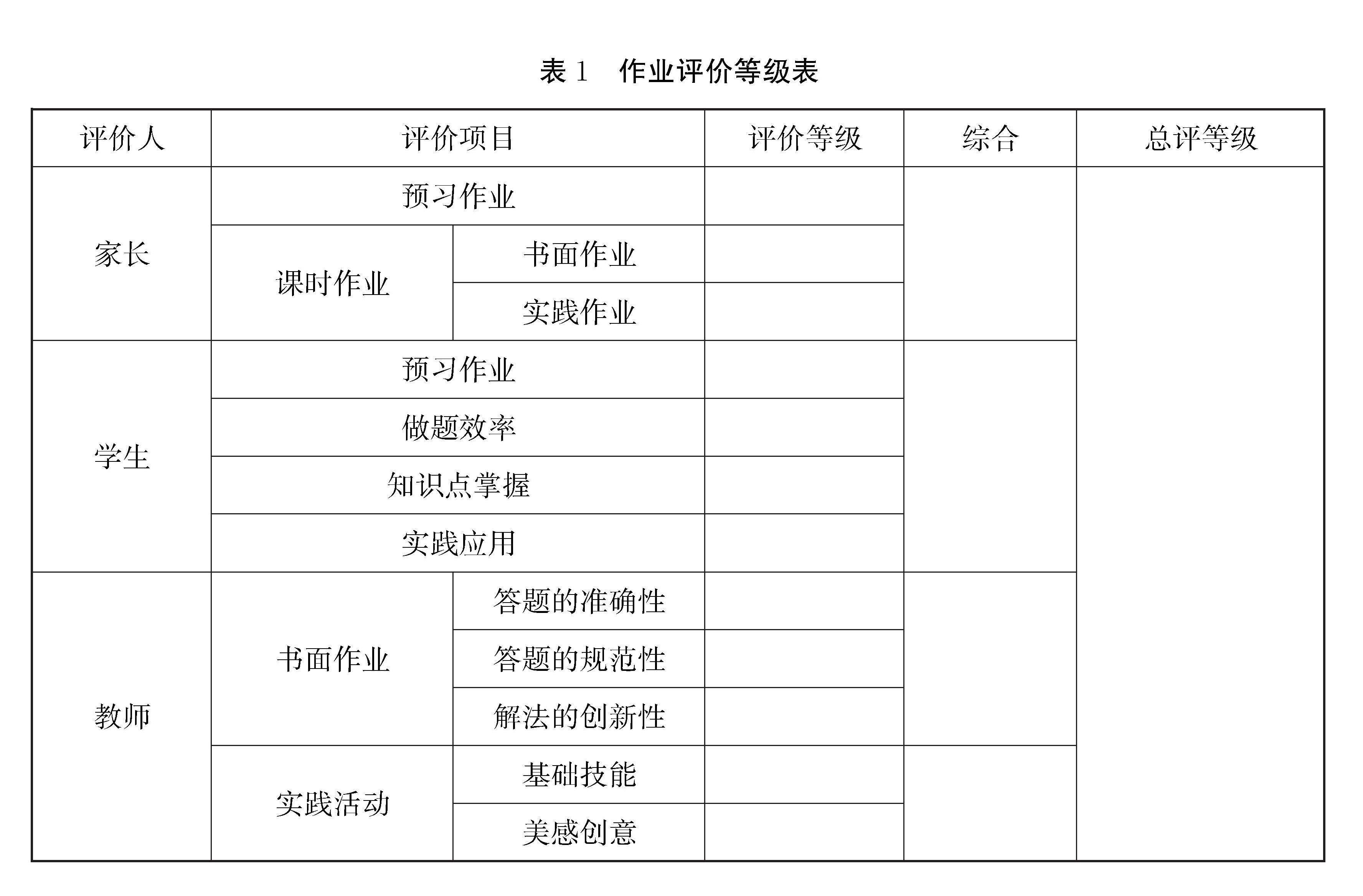
《关于加强义务教育学校考试管理的通知》提到要“完善学习过程评价”。重视学生的学习能力、表现的相对变化程度，从“培养学习习惯—观察学习表现—发展学习能力—提高综合素质”四个维度对过程进行考量。因学生个体能力发展水平参差不齐，教师要用相对进步程度对学生进行评价，给予学生成长的时间，而不是直接贴上标签，避免对学生的自我效能分析产生负面影响。下面是课时作业的评价等级表（如表1）。

对学生进行评价，要让学生在学习准备、过程及结果各个环节得到反馈，不以正确率为唯一标准，以相对变化为评价学生的新标准，建立学生学习档案，观察阶段性变化趋势。这样就能解决很多学生的“瘸腿”现象，促进学生的个性化学习。

（三）创新性原则

作业中原创题的新颖性，能提高学生作业兴趣，从而激发学习内驱力，达到提升学生学习效率的目的。

例3  3月8日早上，小红的妈妈收到了一条信息如下图，意思是  i miss you

本题灵感来自早期收到的一则短信息。学生探索兴趣盎然，利用中心对称图形的定义找正确的语义，几何直观能力及中心对称的模型观念得到培养。

（四）精简性原则

设计作业的重要原则之一就是精简。根据“双减”精神，作业量要减少。但要达到减量增效的目标，作业就必须要精，这样才能真正落实减负。

例4  如图，在已知的平面直角坐标系中，△ABC的顶点都在正方形网格的格点上，若点A、B、C的坐标分别是A（-2，1）、B（-3，3）、C（-1，4）。

①作出△ABC关于x轴对称的图形△A1B1C1，并写出此时B1的坐标；

②若点P（a，b）是△ABC内任意一点，其关于y轴的对称点是P1，求点P1的坐标；

③在y轴上直接画出点Q，使QA＋QB最小。

（五）反馈性原则

作业设计的最后环节是收集学生作业评价的反馈情况，一是为了统计学生的学习情况，二是方便针对班级学生情况调整作业设计的效度，如下表2：

三、初中数学分层作业的甄选方法

（一）分层测评方法

通过准确评估学生的数学能力水平，可以将学生分为不同层次，从而为他们提供适合的作业内容和要求。常见的分层是根据学生的日常数学成绩将学生分为优秀、良好、中等和较差等几个层次；或者基于学生的诊断测试结果进行层次划分，通过测试学生对数学知识和能力的掌握情况，将学生分为不同层次；还可以根据学生参与度和主动性进行分层，通过观察和分析学生的学习态度和参与度，提供相应难度和要求的作业。

（二）多元智能培养方法

根据学生的特点，设计适合不同智能类型学生的数学分层作业，充分挖掘和开发学生的各种智能潜能，提高他们的学习兴趣和动机，实现个性化、差异化的数学学习。

1.关注学生的多元智能类型

根据霍华德·加德纳提出的多元智能理论，智能类型包括逻辑数学智能、空间智能、语言智能、人际智能等。教师需要充分了解学生的智能类型和特点，针对不同的智能类型进行任务设计和组织，以促进学生在数学学习中发挥其擅长的智能。

2.注重多元化的教学策略

针对不同智能类型的学生，教师可以采用不同的教学策略和方法进行数学教学。比如，对于擅长逻辑数学智能的学生，可以提供更多的逻辑推理和问题解决的机会；对于空间智能较好的学生，可以侧重培养他们的几何思维和空间想象能力。灵活运用不同的教学策略，能够更好地满足学生的学习需求，提高他们的学习效果和兴趣。

四、总结

可采用实验设计或长期的教学跟踪研究，对初中数学分层作业的甄选进行验证，以获取更加客观和具体的结论。学校在教研上投入更多的力量，教师在作业设计上精心甄选题目，让学生的脚步轻盈起来，前往立德树人的高速通道也将越来越宽。

参考文献：

［1］孔丽丽.高中化学作业现状的调查与实践研究［D］.石家庄：河北师范大学，2014.

［2］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学大学出版社，2022.

［3］石冲.培养初中生良好数学作业习惯的研究［D］.重庆：重庆师范大学，2016.

［4］教育部办公厅关于加强义务教育学校作业管理的通知［EB/OL］.http：//wap.moe.gov.cn/srcsite/A06/s3321/202104/t20210425_528077.html.

责任编辑：黄大灿