问题引领 提升效能

金瑜

[ 摘 要 ]“问题解决”是发展学生学习能力、提升学生数学素养的重要途径.在复习教学中，教师应结合教学实际设计有效的问题，让学生在问题解决的过程中完成知识的梳理、经验的积累和认知结构的完善，以此提高课堂教学实效，提升学生数学素养.

[ 关键词 ]问题解决；教学实效；数学素养

“提质增效”是一线教师的共同追求.为了实现“提质增效”这一目标，教师不妨将“问题解决”应用于复习教学中，让学生在问题解决过程中学会思考、学会探究、学会合作，从而让学生走上真学之路，有效地提升课堂教学效能.笔者在“尺规作图的复习”教学中，以“问题解决”为主线，通过问题引导学生自主探究，取得了较好的教学效果，现将教学过程简单地呈现给同行，供参考.

课前分析

尺规作图是初中生应具备的一种基本能力.本节课作为初三的一节复习课，旨在通过对五种基本作图及较复杂的尺规作图问题的深入研究，让学生把握尺规作图的本质，提高学生的作图识图能力.

虽然学生已经学过，且已掌握五种基本作图，并具有一定的解决综合性问题的能力，但是学生面对复杂的作图问题时，还是会出现障碍，并因思维受阻而陷入僵局.基于此，本节课的教学目标是让学生灵活运用基本作图的策略和方法去解决较为复杂的尺规作图问题，感悟类比、转化等数学思想方法的价值，培养学生的逻辑推理、直观想象等综合素养.

教学过程

1.动画引入，激发兴趣

动画演示：教师用几何画板演示长方形ABCD沿过点B的直线翻折的过程（如图1）.

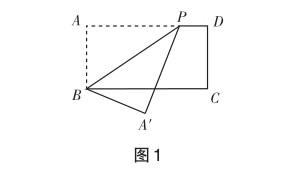
问题 结合以上翻折过程说一说点A的运动轨迹是什么.如果折痕位置确定，你能找到点A吗？反过来，如果给出点A，如何确定折痕呢？

教学说明 复习教学若一直延续着“梳理—练习”这一单一模式，很容易让学生产生枯燥乏味的感觉，影响教学效果.而借助多媒体直观、动态、形象的教学优势，可以快速吸引学生的注意力，激发学生探究尺规作图的热情.

2.复习回顾，促进生长

问题 利用没有刻度的直尺和圆规可以作哪些基本图形？说一说作图步骤及理由.

师生活动 教师先让学生动手做一做，然后通过交流总结五种基本尺规作图的步骤及作图的理由.

教学说明 在问题的引领下让学生通过动手操作回顾五种基本尺规作图的方法，反思五种基本尺规作图的过程及缘由.在此过程中，教师将回顾、梳理、总结、归纳的机会交给学生，让学生通过独立思考、动手实践、合作交流等活动理解尺规作图的精髓，从而为解决复杂的尺规作图问题打下坚实的基础.

3.活动探究，提升能力

活动1 如图2，过点P作已知直线的平行线.（保留作图痕迹）

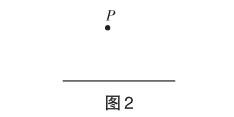
问题1 由什么可以得到平行线？

问题2 结合作图过程说一说你应用了哪几种基本尺规作图.

学生活动 在问题的引领下，学生积极思考，并给出了不同的作图方案（如图3）.

教学说明 开放探究问题的创设，为学生提供了广阔的探索空间，使学生的思维更加活跃.教学中，教师没有直接让学生操作，而是让学生思考“由什么可以得到平行线”，引导学生执果索因，培养思维的深刻性.同时，探寻多种解决问题的方案，不仅可以发散思维，提升教学效果，而且可以让学生进一步体会到，无论应用哪种作图方案，最终都会回归于五种基本作图方法，由此明确复杂的尺规作图均可以转化为五种基本尺规作图，帮助学生认清尺规作图的本质.

活动2 如图4，请按照如下要求作图.（作图工具：不带刻度的直尺和圆规）

（1）如图①，已知△АBC（AC

（2）在图②中作Rt△DEF，使直角边EF落在BC上，且△DEF的周长等于线段BC的长.

图4

问题1 若想构造等长线段，可以应用什么性质？

问题2 在分析尺规作图问题时，画“成型图”是一种有效的解决方案.假设已知Rt△DEF，怎样画出它的“成型图”呢？

追问 在作△DEF时，D，E，F这三个点应该按照怎样的顺序来确定呢？

问题3 请说一说你的作图过程、作图理由，并说一说作图过程中用到了哪些基本图形.

师生活动 教师投影展示学生的作图结果（如图5、图6），并让学生陈述作图过程

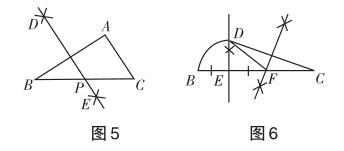
教学说明 以上两个问题呈现递进关系，活动1的作图经验为活动2的解决提供了前提.探究活动1时，在问题的驱动下，学生易于发现利用平行线的性质是构造等长线段的有效途径，由此打开解题的突破口.在研究问题2时，教师让学生体会“成型图”的价值，从而为复杂作图问题的解决提供方法.问题解决后，教师继续让学生思考作图过程中应用了哪几种基本作图方法，由此进一步让学生体验复杂的尺规作图问题实质是基本图形的组合.

活动3 如图7，将矩形ABCD折叠，使BC落在对角线BD上，折痕为BE.你能用尺规画出折痕BE吗？

问题1 观察图7，你能想象折痕BE在哪里吗？

问题2 你还能想到其他方法吗？

师生活动 从学生反馈来看，他们根据翻折的性质，很快确定其折痕为∠DBC的平分线，由此通过作角平分线得到了图8①.方法1给出后，教师又鼓励学生寻求另外一种作图方法，于是学生结合等腰三角形的性质，确定点C折叠后的位置后，通过作线段的中垂线画出了折痕，如图8②.

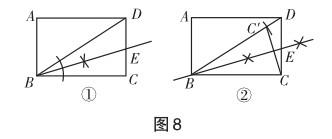
教学说明 引导学生由翻折经验直观地感知折痕，并根据翻折的性质明确作图方法与策略.在此过程中，学生给出一种解决方案后，教师鼓励学生寻求另外一种解决问题的方案，以此发散学生的思维，帮助学生积累丰富的作图经验，培养学生观察、思考和表达的能力，提升学生的数学素养.

活动4 如图9，在矩形ABCD中，点E，F分别在边AD，AB上.用直尺和圆规在线段AB上确定所有的点F，使得△AEF与以点B，F，C为顶点的三角形相似.（请保留作图痕迹）

教学说明 作图时，学生应先尝试画出草图，然后执果索因，这往往是解决复杂尺规作图问题的关键.活动4是一道综合作图题，具有一定的开放性和探究性，有助于培养学生的推理能力和直观想象能力.

教学思考

在本课教学中，教师打破以教师讲授为主的被动的、低效的教学模式，关注学生观察能力、探究能力、表达能力、总结概括能力等综合能力的培养.教学中，教师从整体出发，通过环环相扣的问题将课堂推向一个又一个高潮.

在引入环节，教师借助几何画板直观、形象、生动等教学优势点燃了学生数学探究的热情，为学生营造了一个宽松的、和谐的学习氛围，为课堂的高效生成打下了坚实的基础.在复习回顾环节，学生在问题的引领下主动去探索、去归纳、去总结，以此通过积极参与让学生明晰了基本作图的过程和缘由，为接下来的探究活动做好了知识储备.在探究环节，教师聚焦于巩固基本作图，通过活动引导学生分别研究了与三角形、四边形和圆有关的三类作图问题，让学生明晰复杂作图问题实质上就是若干基本作图的组合.以上教学环节紧密联系、环环相扣，通过有效问题的创设紧紧地吸引了学生的注意力，让学生在思考、实践、反思中领悟了尺规作图的本质，强化了转化、类比的数学思想方法，促进了学生数学能力的提升和数学核心素养的落实.

总之，复习教学中，教师要避免简单的知识罗列和机械的试题练习，应重视设计系统且有内在联系的问题，以此让学生在问题的引领下主动思考、探索与实践，在巩固知识的同时，获得新的生长，提升数学素养.