抓住时机适时点拨，引导学生自我发展

陈玉梅

【摘 要】文章从青蛙爬台阶的故事，探讨促进小学生自我学习数学获得成长的意义及其带来的教学启示。教师在教学中要激活学生已有的积极经验，促进儿童自我“习得”，认清教学的“最近发展区”，重视适时点拨，引导学生自我完善。

【关键词】自我学习 生活经验 自我习得

雨后，通往学生食堂的一个台阶边出现了一只青蛙，不知是谁出于好玩，将这只青蛙放到了台阶上。青蛙想离开这个地方，两只前爪扒住台阶想爬上一级台阶。可是，台阶有点高，青蛙两只后爪用力伸直，费了好大的劲，还是爬不上去。于是青蛙在台阶上爬来爬去，来回都碰到了墙壁，赶紧再折回头爬。这样来回爬了好一会儿后，青蛙开始贴着一侧的墙壁，奋力往上爬。可是墙壁太滑，它还是没有爬上去。就这样尝试了好久，青蛙还是没能爬上台阶。有人说，看来它只有往下跳才行了，不然会不会晒死在这里呀！还有人说，其实它可以跳上台阶的。突然，青蛙像听懂了人话似的，突然用力往上一跳，在大家的惊呼声中，它真的跳上了一级台阶。它想继续往上，又开始了刚才的向上爬行尝试，还是不行，于是又跳，又成功了。后来，我们发现青蛙不再尝试向上爬行了，直接一级一级往上跳，速度越来越快，很快就离开了大家的视野……

这个偶然看到的青蛙跳台阶故事，实际上可以作为动物学习的经典案例。它引发了笔者关于学生学习的几点思考：

1.激活积极经验

青蛙来回尝试往台阶上爬没有成功，又沿着一侧光滑的墙壁爬了几次，也没有成功，有了失败的经验后，它不再尝试，最终改为跳台阶。虽然这是失败的经验，但这种经验，成为后续积累成功经验的先导和基础。学生的学习是以已有经验为基础的，而已有的经验中既有积极的经验，也有消极的经验。教师教学中既要帮助学生克服消极经验的负迁移，也要注意更多地激发并盘活学生既往的积极经验。

例如“千米”的教学，其重点是帮助学生建立“千米”的概念，而学生在日常生活中已经积累了有关“千米”的生活经验，但还不够充分，不够集中。教师在进行数学教学设计时，就要充分考虑到这一点，应采用多种方式帮助学生丰富生活经验，激活已有经验。课前，需要引导学生开展个性化的活动，如借助手机相关软件，走一走，感知从家到哪里大约是1千米，从家到学校是大于，还是小于1千米，走1千米用了多长时间等，让学生初步感受1千米的长度，建立1千米的长度概念，个性化地积累有关1千米的具体经验。课中，引导学生开展交流活动，交流课前积累的关于1千米的经验。但这种经验是个性化的，对于每个学生个体而言是有益的，但其他学生并不能与其产生共鸣。因此，课上继续开展共性化的分享活动，带着全体学生到学校操场，开展从10米到100米再到1千米的走路活动，让学生多视角地积累1千米的长度经验。课后，拓展延伸认知活动，如从1千米扩展到几千米，或同样是1千米，学生使用不同的交通工具花费多长时间，加深和丰富学生对“千米”的感性认知。

2.促进自我习得

学生的学习是一个自我习得的过程。如同青蛙在不断碰壁后不再尝试向上爬行，而是改变了策略，用“跳”的方式，这是青蛙的“自我习得”。学生在学习中也是这样，有的时候教师需要让学生先碰碰壁，使其形成与正确认知相对立的错误认知，而不是提前搭建缩短认知差距的铺垫台阶。因为，有时认知过程过于平直，学生反而没有比较、印象不深。

例如，教学北师大版数学六年级下册“列方程解决实际问题”时，教师出示例题：大雁塔高64米，比小雁塔高度的2倍少22米，小雁塔高多少米？学生尝试解答，大部分学生采用的是算术方法，将算式错列成：64÷2-22或者64÷2+22。也有少数学生用的是方程解答。教师通过当堂举手的方法进行统计，让学生看到，用算术方法解答的人，正确率很低，而用方程解答的人几乎都做对了。为什么会出现这种情况呢？通过引导发现：用方程解答的学生，顺着题意很容易找到数量关系，即小雁塔的高度×2－22=大雁塔的高度，然后设小雁塔的高度为x米，根据数量关系直接列出了方程，就很容易解答。而用算术方法解答的学生，由于对数量之间的关系不是很清楚，导致解题思路的错误。即使以算术方法正确解答的学生，解题时也要将基本数量关系式变形为：（大雁塔高度+22）÷2=小雁塔高度。而在进行数量关系变形的过程中，思路不清晰就很容易出错。通过比较，学生体会到，用方程解答是顺着题目的意思找数量关系，题目怎么说，就怎么写关系式，列出方程，因而是“顺思路”解答。这样，学生经历了一个先“碰壁”的过程，就能更加深刻地体会到方程解答的优势，因而从心理上更容易接受方程解答方法。如果教师出示例题后，直接告诉学生因为方程解答“顺着思路”比较好，所以要求大家用方程解答，学生是没有这样的深刻体会的。“碰壁”后学生往往会主动选择以方程解答的思路，就像青蛙反复想从侧壁爬上台阶，发现努力多归于失败，就会主动放弃“从侧面爬”的动作，改为选择“跳台阶”的方式一样。

3.认清“最近发展区”

所谓“最近发展区”，通俗地说，就是设置的目标要让学生“跳一跳，够得着”。教学目标设置要基于学生的基础，但又要适当高于学生的现有认知水平，具有一定的挑战性。

例如，有这样一道题目：在一次联欢会上，6份相同的奖品被藏了起来。请李力和王刚两个同学一起去找回这些奖品，直到6份奖品全部被找到。要求解释，为什么李力不可能恰好比王刚多找到一份奖品？

学生对此题可能会如何解决呢？

方案一（初级水平）：运用经验，用列举的方法，找到所有的可能情况—6=1+5=2+4=3+3=4+2=5+1，说明结论；

方案二（中级水平）：运用恰当的策略，找到所有可能的情况，解释中涉及了一些关于奇数和偶数的内容，但未能清晰指向两数和的奇偶性；

方案三（高级水平）：如果李力恰好比王刚多找到一份奖品，那么两人的数量必然一个是奇数，一个是偶数，但是任何一个偶数，只能分解成两个奇数的和或者两个偶数的和，而不可能分解成一个奇数和一个偶数的和。因此，李力不可能恰好比王刚多找到一份奖品。

教师的教学要基于学生已有的知识水平，并适当拔高。如果硬要将初级水平拔高为高级水平，对于不少学生而言就有难度，学生也不一定能理解、接受。

试想，上述故事中建立新技能的台阶如果设置太高，青蛙再怎么努力也跳不上去，其多次尝试后的结果就只能是放弃。对于中等水平的学生，教师可以适当点拨，在引导其理解知识的过程中，引导其抓住本质，抓住实质即为“两数和的奇偶性问题”。

4.重视适时点拨

新课标强调教学“以学生的学为中心”，同时也要关注教师主导作用的发挥。青蛙其实是听不懂人话的，它的“向上一跳”纯属条件反射的某种本能。但学生不同，他们是有思想的人。在其思维浮于表面或出现困顿时，教师适时发出的哪怕是一个质疑的反问，一句点拨的话语，就能引发学生的思维向更深层次漫溯、延展，从而获得发展。

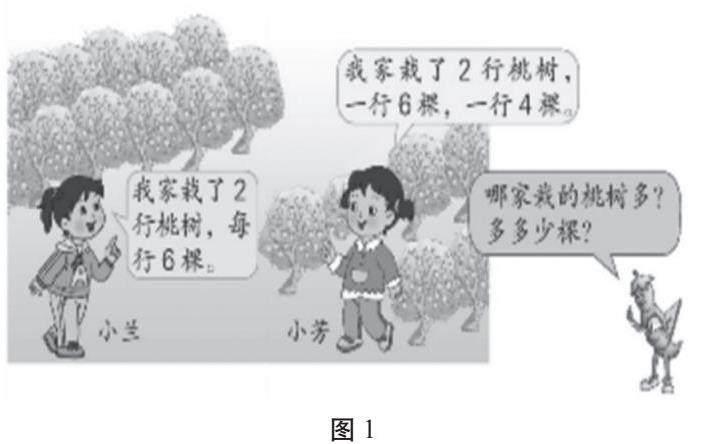
例如，“加法与乘法的对比”练习课教学中，有这样一道练习题（如图1）：

一般教师只会教到乘法和加法不同结构的对比，而有经验的教师会看到乘法和加法的联系，会在教学中恰到好处地进行两次适时的引导、点拨。

第一次：当学生说到求“2行桃树，每行6棵”用乘法；而求“2行桃树，一行6棵，一行4棵”只能用加法时，教师及时提问“只能用加法吗？”，一个反问句，就能引导学生思考：当加数不相同时，只要可以变成相同的加数—两个加数都看成5或两行都看作6棵，再去掉多看的2棵或者两行都看作4棵，再添上少看的2棵，这样仍然可以用乘法计算。这样思考、理解、列式，学生能进一步理解乘法的本质，增强了思维灵活性，促进了学生智慧的生成。

第二次：当学生都用先算后比较的方法时，教师适时提问—一定要算出小兰家和小芳家各栽了多少棵才能比较吗？又是一个反问，学生马上转入新的思考中，重新审视题目的条件和问题、观察数据的特征，进而另觅蹊径、逐行比较，茅塞顿开：小兰家和小芳家都栽了2行桃树，第一行都是6棵，第二行小兰家比小芳家多2棵，所以小兰家栽的棵数多，多2棵。这就可以培养学生敏捷的思维，以及不满足于问题基本解决的“小富即安”。这就说明，教师必须站得高，适时灵活引领、巧妙点拨，重视培养学生思维的高等级品质，才能将教材挖得深入、引得到位。倘若教师在教学中时时都能关注启发学生思维向更深处延展、开掘、扎根，那么学生就能学会思考，体会到思维的乐趣。

5.引导自我完善

就如青蛙上台阶是一个自我修正、自我完善的过程一样，学生的学习也是一个自我不断试误、不断完善的过程。教师只有引导学生经历这样的一个过程，学生的学才是深刻的、牢固的。教学中简单地告知答案虽然省时高效，但由于是外部强加的，因此学生记得快，忘得也快。

例如，“用数对确定位置”教学中，为了让学生感受数对确定位置的便捷、清晰，教师设置了由教师口述几个位置，学生逐一记录的环节。在报出一个个位置的过程中，教师的语速由慢逐步变快：小芳第四列、第五行；小明第三列、第二行……然后问学生：你们记下了各人的位置了吗？大部分学生都皱着眉头，说老师讲得太快了，来不及记录，也有少部分学生记录下来了。这时，教师引导学生交流后发现：有的学生记录的是完整的表达“第几列、第几行”，有的学生却用的是简洁的诸如“四五”的汉字方式或阿拉伯数字记录的“4、5”。教师让其说说自己这样记录的理由，并引导大家比较并说说更喜欢哪一种方式。通过讨论、交流，学生达成共识：用阿拉伯数字记录的方式快速，简洁、清晰。这样用数对记录位置成为学生发现的结果，他们更深切地感悟到数对表示位置的必要性。这就是说，数对表示位置的方法不是外在硬塞给学生的，而是学生在适宜的学习情境中自然生长出来的新认知、一种内在的自我需要满足的结果。

总之，教师在教学中要关注学生自我成长的力量，同时施以恰当的引导，让内因和外力同时作用，促进学生在原有基础上自我发展、顺势发展。