“以生为本”理念下的数学教学实践与思考

姜玉娟

［摘  要］ 新课标背景下的数学教学应将学生放在首位，践行“以生为本”的理念是实施课堂教学的基础. 研究者以“函数的平均变化率”的教学为例，分别从如下四个方面展开教学与分析：关注学情，用问题制造认知冲突；精心预设，科学点拨促思维发展；尊重差异，深入探究扬长避短；转换立场，从学生的视角看问题.

［关键词］ 以生为本；平均变化率；教学

随着新课改的推进，“以生为本”理念成为广大教育工作者的共识. 不论是课堂导入，还是探究活动，抑或例题讲解、练习训练与归纳总结等，都需要将学生放在课堂教学的首要位置. 教师应给予学生充足的探索时间与空间，引发学生独立思考与自主学习，以促进学生思维能力、交流能力与表达能力的协同发展. 本文以“函数的平均变化率”的教学为例浅谈如何践行“以生为本”理念.

关注学情，用问题制造认知冲突

践行“以生为本”理念，首先要了解学生，对学生的思维水平与学习经验有一个宏观的认识. 维果斯基研究发现，每一个人的认知存在两个水平，分别为已有水平与可能达到的水平. 已有的认知水平主要表现为能独立自主地解决问题，有可能达到的认知水平主要表现为无法独立完成任务，但通过学习可解决问题，处于这两个水平之间的为最近发展区. 在教学中，教师需根据学生的最近发展区来挖掘潜能，驱动学生的探索欲.

立足学情，把握好教学进度与难度，设计处于学生最近发展区的问题，能让课堂张弛自如. 尤其是借助学生感兴趣的教学方式，如小组合作、同桌交流、组间讨论等方式实施教学，可让学生在自由开放的环境中对问题进行自主探索与发现，这对发展学生的探究能力与数学精神具有重要意义.

教学片段一

问题1 （借助多媒体播放游乐场过山车的视频，过山车时快时慢，乘客时而安静时而尖叫.）大家坐过过山车吗？

生（众）：坐过.

師：坐过山车给你们带来了什么感觉？

生1：太紧张刺激了，想起来就兴奋.

生2：俯冲的速度太快，小心脏有点吃不消.

问题2 河南商丘的银杏树历经2000多年的生长，现在已经达到20多米高了；雨后春笋能在2天内长出15 cm. 你们觉得银杏树和春笋的生长速度，谁更快一些？

生（众）：春笋.

师：为什么呢？

生3：相同的时长内，春笋生长的高度要大于银杏树生长的高度.

问题3 观察以上两个情境，会发现有些变化比较明显，有些变化却不容易被发现，怎样用数学来刻画这些变化呢？

分析 前面两个问题情境是学生熟悉的生活现象，问题的提出瞬间就拉近了学生与知识的距离，学生的思维也变得活跃. 第三个问题情境则从专业的角度来启发学生的思维，成功引发了学生认知冲突，让学生对这些现象产生了探索欲. 整体来看，每一个问题都是在“以生为本”的基础上，从最近发展区出发而设计的，激活了学生的思维，让学生迅速进入了探索状态，尤其是第三个问题的提出，让学生产生了进一步探索的欲望，感知本节课学习的重要性与必要性.

学贵有疑，好的问题就是学生思维的载体. 上述三个问题由浅入深、循序渐进，为学生的思维发展搭建了“脚手架”，让学生对本节课的教学充满期望. 众所周知，疑是思维的起点，是探究的原动力，在问题的引领下，学生很快就能进入探索状态.

精心预设，科学点拨促思维发展

学习是一个复杂的智力活动过程，受遗传、环境、家庭、社会等综合因素的影响，每个学生的知识基础与思维能力不尽相同，教师要在充分了解学情、教情与考情的基础上设计教学方案，让有效课堂在精心预设与动态发展中生成. 新课标一再明确学生是课堂的主人，在课堂中占有主体地位. 因此，教师在进行课堂预设时，须将学生的主体参与度考虑进去，让课堂在有效互动中动态生成.

虽说课堂是动态变化的，不论多么精心的预设都有可能遇到“意外”，但这并不是让教师忽略预设的“借口”. 事实证明，真正的课堂教学是有计划、有目的、有组织的活动，预设相当重要，这是践行“以生为本”理念的前提与基础. 在精心预设的背景下，学生会更加积极地参与教学活动，并在活动中做好倾听、合作、表达与总结工作，这是促进学生个体成长的重要途径.

如图1所示，精心预设可分为原行为阶段、新设计阶段与新行为阶段，每一个阶段的过渡都离不开反思的作用.

教学片段二

课前，教师精心预设本节课，预期通过六个逐层递进的问题与一些图形为学生创造一个宽阔的思维场域，在学生对问题的逐个分析中适当引导与点拨，以促进学生思维的发展.

预设问题如下：

问题4 （展示篮球运动员姚明的照片）大家认识这是谁吗？（生：姚明.）

问题5 从照片不难看出他很高，有谁知道他的具体身高是多少吗？（生：2.26米.）

问题6 有谁研究过他的身高生长情况吗？（生：没有.）

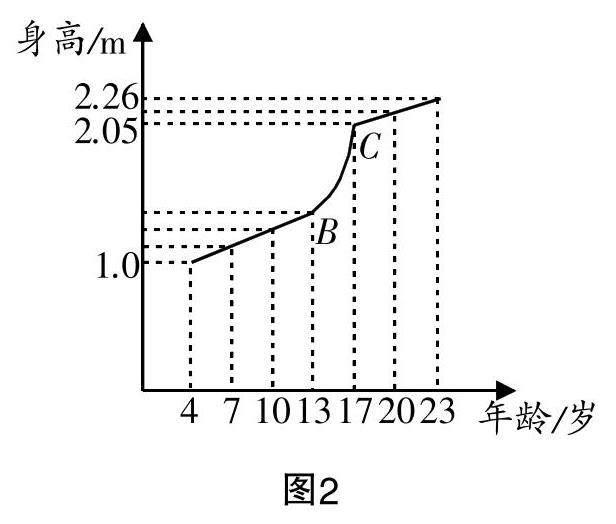
问题7 （借助微视频介绍姚明的出生地、生活小故事与身高生长情况，呈现他的身高随年龄变化的曲线图，如图2所示.）观察微视频，我们对姚明有了一定的了解，从图来看，有什么特点？（生：13～17岁时身高增长速度特别快.）

问题8 在13～17岁时，他的身高曲线有什么特点？（生：特别陡峭.）

问题9 在上一个教学环节中，我们讨论了同一时间段内，春笋与银杏树的增长速度，并明确春笋的生长速度较快. 现在观察图2所示的曲线，发现BC这一段特别陡峭，堪称“峭壁”. 我们可以用什么数学量来量化这段“峭壁”呢？

教学片段三

问题12 若无限小的话，会出现什么情况？（学生的想法很丰富，教师适当引导，为后续“无限小区间”的教学奠定基础.）

问题13 用平均变化率来衡量某种量变化的程度，是否精准？（不少学生认为是精准的）

此时教师展示图3，引导学生自主发现平均变化率所刻画的“陡峭”并不精确，这与生活实际中的物体（质量、速度等）的平均类似.

以上教学环节，在教师的精心预设与恰当引导下，学生对本节课所学的概念的理解更加透彻，并在心中种下了一颗种子：究竟该用怎样的量来描述陡峭程度更准确呢？正因为如此，学生对接下来的教学充满了期待.

尊重差异，深入探究扬长避短

哈佛大学的加德纳教授提出多元智能理论，他认为每一个学生都拥有不同程度的九种智力，各个智力因素之间因为组合不同而表现出不一样的智力水平. 在多元智能理论的指导下，每一个学生都拥有不同的特长、心理倾向与学习风格. 教师应关注学生客观存在的个体差异，并最大化地尊重学生的这种差异，尽可能张扬学生的个性，提升教学实效.

教学片段四

有甲乙两个容器，虹吸管将甲容器内的水吸到乙容器内，经过t秒后，甲容器内水的体积为V（t）=5e-0.1t（cm3），第一个10秒内，甲容器内水的体积V的平均变化率是多少？

学生应用平均变化率公式解题，在此基础上，教师设计如下问题要求学生探究：①结论中的“-”号是什么意思？②如果探究对象是乙容器，水體积的平均变化率的符号是正还是负？③第二个10秒内，甲容器内水体积的平均变化率是多少？与之前相比发生了怎样的改变？这些结论分别代表了什么意思？

这些问题是不少学生的“软肋”，有些学生因为没有完全理解题意，运算素养又不够，导致解题失败. 因此，教师放缓教学进度，给予学生更多的鼓励与引导. 尤其是关于“-”号的意思，要让学生在充分理解的基础上进入下一轮探究.

当研究对象换成乙容器时，水体积的平均变化率则变成“+”号，这意味着乙容器内水量处于增加的趋势. 由此可见，前两个问题探究的是水体积平均变化率正负符号相对应的情况. 最后一个问题的探究，需要从水体积的平均变化率的大小出发，根据结论获得第二个10秒内水体积的平均变化率与甲容器内水量的变化速度相关.

在教学中，教师让学生计算后再讨论. 学生经过积极互动与交流，不仅训练了语言表达能力，还提升了数学逻辑思维与推理能力. 一些认知水平较差的学生，受群体的影响积极倾听、交流、跟进，取得了不错的教学成效. 因此，充分尊重学生的个体差异是促进学生个性发展的重要举措.

转换立场，从学生的视角看问题

践行“以生为本”理念，首当其冲的是要站在学生的立场观察与思考问题，这是从真正意义上理解学生的手段. 教师转换立场，可有针对性地提出合理的教学意见，培养学生的“四基”与“四能”. 当然，这也是信任学生，为学生提供自由空间的举措. 学生通过交流、纠错、互评等方式能不断促使自身成长.

教学片段五

当师生共同探索完“函数f（x）=2x+1与g（x）=－2x在区间［－3，－1］和［0，5］内的平均变化率”后，教师再引导学生探索“一次函数f（x）=kx+1在［m，n］内的平均变化率”，鼓励学生自主解决问题.

学生经探索获得结论：直线的平均变化率只与该直线的斜率相关，和其他任何量都没有关系.

追问：直线的斜率与平均变化率一样，是否可以称斜率就是平均变化率呢？

在实践中，不少学生主动提出斜率是零或者不存在的情况，这是超越教师课前预设的情形，纯属“意外”. 但教师没有回避情形，而是顺应学生的思维包容这些“节外生枝”，与学生共同比较分析，让学生尽可能从已有的材料中进行猜想与推测，并加以验证. 这不仅体现了“以生为本”理念，还发展了学生的创新意识.

总之，在课堂教学中，一定要将学生放在首位践行“以生为本”理念，这既是激发学生思考与探索的基础，也是培养与发展学生创新能力的关键.