体验、比较、推理：量感生长的重要路径

陈炜

【摘 要】量感作为一种核心素养表现，指的是个体对事物的可测量属性及大小关系的直观感知。小学阶段的三个学段中都包含了与量感相关的内容，是数学课程的重要教学目标之一。那么，在课堂教学中应如何培育学生的量感素养呢？体验、比较和推理是量感培育的三条重要路径。

【关键词】体验 比较 推理 想象 量感

量感是《义务教育数学课程标准（2022年版）》中新增的一项重要内容，是核心素养的主要表现之一。加强量感培养有助于学生把握数学本质，有助于学生形成完整的数学知识体系，有助于养成定量描述客观世界的习惯。因此，在小学阶段教学中，培养学生的量感尤为重要。本文将从适宜小学生量感生长的路径进行分析，提出可行性操作策略。

一、注重体验，形成具身经验

具身认知理论认为心智离不开身体的体验，强调身体在认知过程中的主体作用。尤其小学生量感的培养是从对量的感受开始，因此应重视让学生的身体深度参与认知，形成自身经验。在生活中，学生对事物的大小、长短、轻重等可测量属性有着初步的感知，但是学生最初对这些量的感知是比较片面、模糊的，要在反复体验中不断修正，从而逐步建立清晰的表象。当学生看到高楼时，他会发出“这栋楼好高啊”的感叹，把学生头脑中的“好高啊”转化为数学知识的“多高呢”，就是量感的建立过程。例如，在教学人教版三上“周长”时，为了让学生对周长的概念有更深入的理解，教师设计了指一指、描一描、围一围、画一画、量一量等活动，在多种具身体验的过程中使学生充分认识周长的概念，并在概念建构中凸显量感的生成。

在“量感”的培育中，帮助学生建立体感的定量是至关重要的。量感并不是教师教给学生的，应该是学生在大量的数学活动中，具身体验逐渐形成的。例如，在教学人教版二上“认识厘米”相关内容时，教师先让学生在直尺上寻找1厘米，比画1厘米的长度，然后让他们闭上眼睛在头脑中想一想1厘米的长度，接着拿出没有刻度的直条在练习本上尝试画出1厘米线段的长度，最后利用刻度尺量一量所画线段的长度是否为1厘米。学生通过找、说、比、想、画、量等操作活动，充分体验1厘米的长度，从而形成1厘米的标准单位定量。当学生已经初步认识1厘米之后，教师再请学生取出课前提供的信封中的物品，找出其中长度大约是1厘米的物品，让学生独立观察、同桌交流、合作测量。最后寻找身边1厘米的事物。通过对给定事物的观察、交流、测量，学生深入地体验1厘米的单位长度，确定1厘米的体感定量。

二、加强比较，提升理性认识

学生的量感从模糊到清晰，从浅层到深入，还需要借助比较，在对比中增强量感。学生对于不同事物的同一可测量属性，先是直观比较，当直观比较无法得出结果时，会思考通过中间物来进行间接比较，最后创造出一个“标准”对数量进行比较。

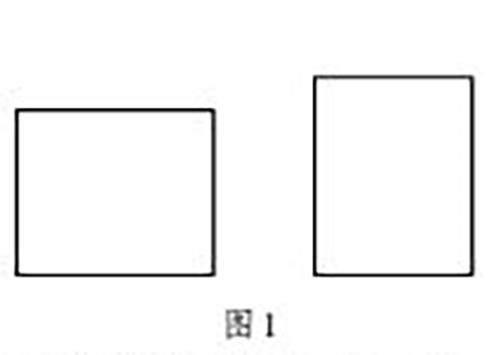
例如，在人教版三下“面积和面积单位”的教学中，学生对生活中物体的面的大小是有初步感知的，教师先让学生结合生活经验，举例说明什么是面积，在小组交流中初步建构面积概念。接着，教师让学生在教室里找到两个物体的面，比一比它们的大小，加深理解。然后，放手让学生探究学习单中的学习任务：比较图1中的两个图，哪个图形的面积大？在这一核心探究任务中，因为两个图形的面积相差不大，学生很难通过观察直观比较两个图形的大小。另外，两个图形的形状也不相同，用重叠的方法也不好比较两个图形面积的大小。学生带着困难与疑问进行探究，激发了求知欲。进而，教师引领学生寻找解决问题的途径，学生由此表达了两种想法：（1）用其他小的图片来测量，如圆形、三角形、正方形，看看这两个图形里面分别有几个这样的小图形。显然在用圆形、三角形进行测量时，由于小图形填充大图形时有较大的间隙，导致测量出的结果并不准确，通过对比发现用小正方形正好能铺满，这是学生对度量单位的初步认知。（2）把两个大图形分割成一块块大小相同的小图形。

教师通过布置任务制造认知冲突，激发学生的探究欲望。学生想到把这两个图形分割成一块块小图形进行比较，这其实就是在用“非标准单位”来进行度量，产生用度量解决问题的需要，进而感受度量的意义。尽管学生自己想到的单位可能是“非标准单位”，却可以为引出后续学习“标准单位”作铺垫。在对比中发现，用大小一样小正方形进行填充，才能准确比较出两个图形的面积大小。因此，统一面积单位的必要性便油然而生。通过以上的操作、思考、分析、对比的过程，使学生对面积单位的认识由朦胧变清晰。

三、推理想象，促进量感发展

并不是所有的量感都能在活动中感悟，还需要学生在丰富的想象中，通过数学推理來获得更多感悟。在小学阶段的数学学习中，包含较大度量单位，如千米、吨、公顷、平方千米等度量单位。这些概念本身对于小学生来说不仅“大”而且离学生“远”，这是由于在课堂上很难直观展示1吨的轻重或是1千米的长度让学生具身感受，因此这些大单位的量感建立是有难度的。在教学时，不仅需要教师引导学生在熟悉的日常生活场景中去体验，建立表象，更需要教师联系之前学过的、相对小的、熟悉的单位，引导学生在推理想象中，建立对这些“大量”的认识。

例如，在教学人教版三上“千米的认识”时，显然在教室里无法展示1千米的真实长度，学生无法直观感受“1千米有多长”，因此建立1千米的正确表象有一定的困难。在教学中，可以鼓励学生在认识“米”的基础上展开想象，进行推理。教师抛出问题：“1千米有多长？”让学生结合经验，独立思考后小组内交流汇报。生1：“操场一圈长度是200米，5圈的长度就是1000米。”生2：“以1个小朋友张开手臂长度大于是1米为标准，那1000个小朋友张开手臂的长度叠加大约是1000米。”教师现场请10位同学手臂张开，长度约10米为标准，让学生想象100个这样的长度就是1千米。生3：“一间教室长约8米，125间教室的长就是1000米。”以这样的方式感受1千米，让学生结合旧知，在体验、比较、想象、推理中建立间接经验，然后对间接经验进行多次叠加，得到1千米，这和度量“量化”的含义不谋而合。学生亲历回顾、类比、计算、操作、推理等一系列的学习过程，形成对1千米的深刻感知。

此外，学生度量策略的形成与发展，也有赖于数学教学过程中注重学生量感推理能力的培养。教师可以引导学生经历推理、判断、猜测等过程，促进学生量感的形成。某市一次六年级数学测试中有这样的一道题：以下选项中质量最接近1吨的是（ ）。A.50瓶矿泉水，B.200个鸡蛋，C.25名六年级学生的体重，D.1000枚1元硬币。此题考查的是量感，全市学生正确率达不到70%，究其原因，并非六年级的学生不懂得克、千克和吨，也不是不知道矿泉水、鸡蛋、体重和硬币的轻重，而是因为这部分学生不会进行推理，不能很好地进行单位之间的换算。教师在日常教学中，让学生经历猜测、动手验证、反思与修正的过程，才能促进他们思维能力和数学素养的提升。学生只有既具备量感的相关知识，又具有数学分析和推理能力，才能全面发展量感，提高问题解决能力。

（作者单位：福建省福州市鼓楼实验小学）