对培养小学生数学推理能力的思考与实践
2024-05-29颜冬芹
颜冬芹


[摘 要] 推理是数学的基本思维方式,是学好数学的前提和保障,推理能力的发展贯穿学生数学学习的始终。在日常教学中,教师要有意识地设计一些充分展示数学规律形成、发展及运用过程的问题,引导学生在过程中积极思考、大胆猜想、科学验证,以此培养学生积极主动探索的精神,有效提高其数学推理能力。
[关键词] 推理;推理能力;主动探索
数学推理能力是人们一直关注的焦点问题,它影响着学生创新意识和创新能力的培养。在传统教学中,教师常常过度强调演绎推理的重要性,忽视合情推理的价值,这样不仅影响课堂教学质量,而且影响学生可持续学习能力的提升。因此,教师在培养学生演绎推理能力时,要重视培养学生的合情推理能力。教学中,教师应为学生提供一个自由的、和谐的学习环境,设计一些具有探索性的问题让学生猜想、探索、发现、运用,以此逐渐提高学生的数学推理能力。
一、呈现过程,引导归纳推理
教学中,教师可以设计一些充分展现数学规律形成、发展和应用过程的问题,让学生通过观察、分析等过程抽象、概括、运用规律,从而有效培养其归纳推理能力。
案例1 找规律
(1)按要求填表(见表1)。
(2)观察a与b的乘积、a与b的最大公因数和a与b最小公倍数,你有什么发现?
(3)根据上面的发现,如果a与b的乘积是300,a与b的最大公因数是5,那么a与b的最小公倍数是什么?
该问题分为三个层次:一是通过计算为后面的探索提供丰富的素材;二是通过观察、分析等过程,发现和表述规律;三是运用规律解决问题。由此通过计算、观察、分析、概括、运用等过程,能潜移默化地提高学生归纳推理能力。
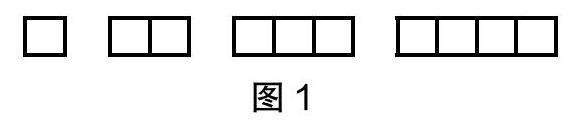
案例2 把边长为1cm的正方形纸片,按照图1所示的规律拼成长方形。
(1)如果按照以上规律继续往下拼,5个小正方形拼成的长方形周长是( )cm。
(2)用m个小正方形拼成的长方形的周长是( )cm。
案例3 小明用计算机设计了一个程序,输入和输出数据(如表2),当输入的数据是30时,输出的数据是何值?
对于此类问题教学,教师不要急于求成,要预留时间让学生观察、思考、交流,重视呈现学生的思维过程,并通过合理地启发和引导让学生发现蕴含其中的数学规律,以此提高其归纳推理能力。
二、基于信息,引导合情推理
三、阅读理解,引导类比推理
教材是专家学者精心编写的,具有科学性、普适性等特点,其在教学中的地位及价值不言而喻。不过不同的地区、不同的学校、不同的班级、不同的学生实际情况有所不同,因此教材存在一定的局限性。在实际教学中,教师要深挖教材资源,并对相关内容进行适度的拓展延伸,以此通过有效拓展不断丰富学生的认知,开阔其视野。此外,教師要结合教材内容设计一些与教材内容相关的拓展训练内容,进而通过与原有知识相类比,逐步培养学生类比推理能力。
案例5 探索“4的倍数特征”
在学习“2、3、5的倍数特征”后,教师鼓励学生继续探索“4的倍数的特征”,以此通过有效拓展与延伸,培养学生类比迁移和举一反三的能力。为了便于学生自主发现规律,教师设计了五个问题。
问题1:我们已经学习了“2、5的倍数特征”,你还记得是怎么发现规律的吗?
问题2:试猜想“4的倍数的特征”是什么?
问题3:算一算,下列各数104, 208,316,428,236,132,258,324,哪些是“4的倍数”?结合百数表“4的倍数”,看一看你有什么发现?
问题4:根据以上发现,在下列各数124,242,264,318,556,846中,用“﹏”画出4的倍数,并通过“算一算”验证你的猜想。
问题5:是否存在一个数,它的末两位数是4的倍数,但是它却不是4的倍数呢?
在教材中学生已经学习了“2、5的倍数特征”,根据已有经验,学生容易从末位数出发,猜想个位是4的数就是4的倍数,虽然这一猜想并不成立,但是为接下来的猜想和验证提供了前提。接下来,教师引导学生回顾最初的探寻过程,将已经验证过的4的倍数的数与百数表中的数相对照,猜想“4的倍数”与末两位数有关,由此通过类比、猜想、验证等过程发现规律,提高学生类比推理能力。这样在环环相扣的问题的引导下,促进了学生思维能力的发展和推理能力的提升。
四、灵活应用,实施演绎推理
数学是一门非常严谨的学科,解决任何问题都应做到有理有据。演绎推理作为数学推理的基本形式,其是在原有知识和经验的基础上,按照严格的逻辑发展得到新结论的逻辑推理过程。在实际教学中,教师要为学生创设自由探索的空间,培养其积极主动的探索精神,在运用知识的过程中提升其演绎推理能力。
这样通过形同质不同的问题引导学生对比分析,并灵活运用分数相关知识进行演绎推理,有利于培养学生思维的严谨性和灵活性,有利于提升学生的演绎推理能力。
总之,培养学生数学推理能力是一个慢过程,教师切勿急于求成,应为学生提供尝试、探索、发现数学规律和数学模型的思考空间,鼓励学生通过观察、对照、猜想、类比等活动主动探索数学规律、验证数学结论,以此逐步提高学生的数学思考能力和数学推理能力。
