新黎曼理论及其应用
2024-05-29朱越


[摘要]新黎曼理论作为分析近现代音乐的重要方法之一,对其研究具有一定意义。本文第一部分简要介绍了“维兹曼域”和乔兹的七和弦转换模型,第二部分运用PLR变换模型并结合前文介绍的两种转换方式来分析肖邦《前奏曲Op28 No9》,并从新黎曼理论视角阐释和弦的相互关系。在分析过程中,笔者还尝试仿照“维兹曼域”构建减三和弦的转换路径并分析作品片段,试图丰富新黎曼理论分析模型。
[关键词]新黎曼理论;和弦转换;
[中图分类号]J614.1[文献标识码]A[文章编号]1007-2233(2024)04-0116-03
[收稿日期]2023-11-01
[作者简介](朱越(2001—),女,安徽师范大学作曲技术理论方向硕士研究生。(芜湖241000) )
一、理论介绍
新黎曼理论是一种用数学模型模拟和弦关系的转换方法,源于大卫·列文(David Lewin)的《一种形式化的广义调性功能理论》,该理论最重要的内容即PLR转换模型和音网,具体内容此处不再赘述,本文将介绍在此理论上衍生的两个概念。
(一)维兹曼域
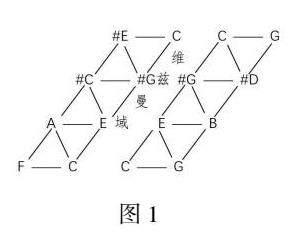
1853年,卡尔·维兹曼(Carl Weitzmann)对增三和弦作出了系统解释。他认为有16 种通过声部间的半音将一个增三和弦与大三或小三和弦连接起来的方式。在此基础上,理查德·科恩根据增三和弦可以将八度均等划分以及可以通过“最俭省的声部进行”产生多个协和三和弦的性质将“维兹曼域”作为构建三和弦转换关系的重要基础。这一理念的提出,将增三和弦纳入新黎曼理论的讨论范围,扩充了该理论的模型。由于音网的右斜方向是按大三度排列的,所以每一条右斜方向的线条都能够构成增三和弦,将这条边拉开,便形成增三和弦的空间,也就是科恩文中提到的“维兹曼域”(见图1),该区域只需变动一个音即可实现三和弦的转换。
(二)艾德里安·乔兹七和弦模型
艾德里安·乔兹(Adrian Childs)在《Moving beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords》中提出了大小七和弦以及半减七和弦的转换模型,在这个模型中乔兹列举出了4-27集合级之间所有可能的两音变动也就是P2(Perturb)关系。
乔兹规定了两种变换系统S(Similar)和C(Contrary),如谱例1所示。S指保留和弦中的两个音,另两个音做同向半音运动,因此以Similar为名,缩写为S。在S的右下方标有数字,前一个数字表示保持音之间的音程级(interval class),后一个括号中的数字表示摄动两音之间的音程级。C指保留和弦中的两个音,另两个音做反向半音运动,因此以Contrary为名,缩写为C。其数字标记和S同理。在P2关系中,根据排列组合原理,C转换应当和S转换一样有6种,但是有些组合在C转换后不能构成三度叠置的七和弦,所以不计入该转换系统内。
2谱例1中,“+”代表大小七和弦,“-”代表半减七和弦,字母即和弦根音,例如“F+”即为F大小七和弦,“F-”即为F半减七和弦。空心音符代表被保持,实心音符代表被弹奏。通过谱例1可以看出,S转换改变和弦性质,C转换保持和弦性质。除此之外,S转换还有着和PLR转换共同的特点——对合性。
这种转换也可以形成类似三和弦音网的转换网络,如图2所示。图中是一个三维立方体转换模型,立方体的八个顶点分别代表一个4—27的集合成员,这八个和弦的音属于同一个八声音阶音集。棱长和面对角线代表转换路径,其中棱长涉及三种S转换,面对角线(虚线)涉及三种C转换,通过这些转换,每个和弦可以直接与除自身外的六个和弦形成联系,也就是说只有一个和弦不能同原和弦形成直接转换,这个和弦与原和弦所在的顶点相对,两顶点相连即为立方体的体对角线(例如“F-”顶点与“D+”顶点)。 这个模型中可以形成两个循环,S2(3)、S5(6)循环和S4(3)、S5(6)循环,这两个循环包含了模型中所有八个和弦。
二、实例分析
这一部分,笔者将用上述PLR转换概念对肖邦《前奏曲Op28 No9》进行分析和总结其在新黎曼三和弦转换理论视角下的特点。此外,笔者还尝试模仿增三和弦“维兹曼域”构建减三和弦分析路径并通过实例分析验证其可行性。
肖邦《前奏曲Op28 No9》为简单的一部曲式,划分为三个乐句,曲式结构如图3所示。
(一)RL/LR链的局部运用
RL循环为RL的复合,这种转换需通过十二次可以形成一次循环,每次转换不改变和弦性质。在这部作品中,出现了不完整的RL和LR链,分别在作品的第1、2、3、10小节。
谱例2为作品的前三小节,其和弦标记在谱例下方。第一小节后三拍的和弦B+、E+、A+形成连续的RL转换,连续上四度移位,将刚刚确立的调性模糊。
第二至第三小节的#G-、#C-、#F-、B+属于连续的LR转换但略有不同。前三个和弦之间的转换关系均为LR,如果第三个和弦到第四个和弦也是LR的话,最后一个和弦应该是B-,但是在谱例中是B+,说明最后两个和弦#F-与B+的转换在LR的基礎上复合了P转换(在LR前后均可)。
(二)调性布局的PL链
正如调性关系是高一级的和弦关系一样,三和弦转换的循环原理在更高一级的调性层面上也是适用的,如上图所示,该作品的调性布局为E—C—bA—E—F—E,F大调所处的位置类似E大调之间的辅助性调性,在分析时忽略不计,这样就只剩下了E—C—bA—E,这种连续下行大三度的调性布局形成一个循环,这正是上文提到的增三和弦的特质,也属于童忠良老师在《近现代和声的功能网》中提到的大三度循环。当我们采用新黎曼三和弦转换理论来分析,该作品的调性布局构成了PL循环,该循环在音网中形成的空间如图4所示。
PL循环由PL两个变换复合而成,其循环周期为三次,产生三个同性质的三和弦,相邻之间为T4移位关系,若将PL拆开来看,PL的交替式变换要经过六次才能完成一次循环,每次变换产生的和弦性质都不同。上例中提到的E+、C+、bA+、E+正属于PL循环关系,这种循环在保持一个共同音的情况下,另两个声部均做半音运动,这个模型解释了浪漫主义时期半音化和声,转换形成的根音关系也与浪漫主义时期作曲家偏爱三度关系契合。
(三)七和弦之间的转换
作品第四小节后两拍的两个和弦分别是#D半减七和弦以及B大小七和弦(见谱例3),从调性和声角度解释二者分别为E大调导七和弦与属七和弦。而这两种和弦刚好属于上文介绍的艾德里安·乔兹七和弦模型,下面笔者将尝试用这个模型分析声部的运动轨迹。
通过乔兹的模型可以了解到,S和C都是以保留两个共同音为前提的转换,谱例中的两个和弦有三个共同音,那么参照PLR复合链,可以推测应该是采用了复合转换。上文中还提到,S转换改变和弦性质、C转换不改变和弦性质,而谱例中的两个和弦性质不同,由此可以排除只含有C转换的复合转换。经过尝试,笔者找出这两个和弦在此模型下的转换方式为S3(4)·C3(4)(见图5),#D半减七和弦先通过S3(4)保持#D、#F两音,A与#C下行半音到bA和C,过渡到bA(#G)大小七和弦,然后通过C3(4)保持#D、#F两音,bA和C做反向半音运动分别到A、B两音到达B大小七和弦。与功能和声的解释相比,用这种模型解释好像麻烦许多,由于这种模型只适用于半减七和弦和大小七和弦之间的转换,笔者目前没有找到合适的谱例,今后笔者会继续寻找适合的谱例。
(四)对减三和弦的界定
在这部作品中出现的七和弦有三类:一类是大小七和弦,在分析时将七音省略把其当成大三和弦看待;还有两类是减七和弦和半减七和弦,不管省略哪个音,都会简化成减三和弦。从笔者目前掌握的资料来看,减三和弦在新黎曼三和弦转化体系中似乎未曾提及。受上文中“维兹曼域”的启发,笔者尝试仿照增三和弦的“维兹曼域”,试图为减三和弦的转化找到较为合理的解释。
之所以仿照“维兹曼域”,是因为音网的构造。在音网中,右斜方向的连续大三度构成增三和弦,相应地,左斜方向的连续小三度构成了减七和弦,而且减七和弦有着和增三和弦一样的八度均分特质,只不过减七和弦把八度均分成四份。在三和弦转换网络中,我们不得不将减七和弦简化成减三和弦,通过观察可以发现,减三和弦在音网中也可以作为中心构成俭省声部进行或者起到过渡的作用。在保持两个音的情况下,减三和弦有四种转换的可能,有的移动半音,有的移动全音。例如C减三和弦,若保持C和bE两音可以通过bG音移高全音和移低半音转换到bA大三和弦和C小三和弦,保持bE和bG两音则可以通过C音移低半音和移低全音转换到bC大三和弦和bE小三和弦。
作品第7小节属于穿越减三和弦区域的运动(见谱例4),第一拍和第三拍的和弦A+与bB-之间为#C减七和弦,我们可以把这个和弦简化为bB(#A)减三和弦。在音网中,A+和bB-分别处于bB(#A)减三和弦构成的区域两侧,这两个和弦在保持共同音的基础上通过bB(#A)减三和弦连接,如图6所示。
图中左侧是常规的音网,右侧是将简化后的#C减七和弦所在的左斜线条拉开后的音网,中间的区域便是减三和弦的地带。通过音网可以清晰地观察到,若将第二拍的减七和弦忽略,那么A+与bB-的转换则属于上文中提到的保留一个共同音的PL关系,即以#C(bD)为倒影轴的转换。当我们把减三和弦列入考虑范围时可以发现,从A+到#A减三和弦的转换为保持两个共同音,另外一个音A做上行半音运动到#A。从bB(#A)减三和弦到bB-的转换同样是保持两个共同音,另一个音E上行半音到F,整个运动都属于俭省声部进行。不难发现,第二种解释方式的半音运动更多,保持了更多的共同音,更加平滑,因此验证了减三和弦加入新黎曼三和弦的转换可行性。
结语
本文在PLR转换模型基础上介绍了“维兹曼域”和乔兹的七和弦转换模型,并尝试用其进行分析谱例。通过分析不难发现,该理论在解释浪漫主义时期调性扩张高度半音化的作品有着突出的优势。然而,这种分析理论的使用范围有一定局限性,例如PLR转换只限于大小三和弦,尽管“维兹曼域”将增三和弦纳入和弦转换的范围,但是仍无法解释三和弦与七和弦的转化,在分析谱例时,七和弦都要省略某个不重要的音,将其转换成三和弦才能进行分析,但这种分析难免会以偏概全,在面对这样的情况时,应该与其他分析理论相结合,在最大限度地保留作品完整性的前提下进行分析。
参考文献:
[1]理查德·科恩.唐小波,高拂晓.“新里曼”理论导论: 一次调查与一次历史的纵览[J.中央音乐学院学报,2017(1):125-135.
[2]谭森.三和弦变换之视角及其技术探析[J.天津音乐学院学报,2022(1):74-88.
[3]高畅.新里曼理论三和弦转换的基本模式及其扩展[J.音乐探索,2015(4):53-65.
[4]李天然.论新里曼分析法在音乐分析中的实践意义——以勃拉姆斯《第二交响曲》第一乐章为例[J.黄钟(武汉音乐学院学报),2022(4):95-107;166.
[5]谭森,贾达群.三和弦变换及其结构组织手法——新里曼理论视域下的舒伯特《降E大调钢琴三重奏》第一乐章探究[J.北方音乐,2023(2):72-85.
[6]高畅.三和弦的逆行倒影链和移位链操作及不同转换模式的循环[J.星海音乐学院学报,2016(2):92-105.
[7]Adrian P. Childs,Moving beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords. Journal of Music Theory. 1998,Vol. 42,No. 2,pp. 182.
[8]COHN R Neo-Riemanninan Operations,Parsimonious Trichords,and Their Tonnetz Representations[J]. Journal of Music Theory. 1997, 41(1):1-66.
[9]COHN R Weitzmanns Regions,My Cycles,and Douthetts Dancing Cubes[J]. Music Theory Spectrum,2000,22(1):90.
[10]COHN R,Maximally Smooth Cycles,Hexatonic Systems,and the Analysis of Late-Romantic Triadic Progressions[J]. Music Analysis ,1996,15(1):10.)
(責任编辑:王肖茜)
