如何利用微元法解答高中物理问题

2024-05-17张玥琳

数理天地(高中版) 2024年6期

张玥琳

【摘要】在高中物理问题中有一类题目其中的物理量并不是恒定的量，它们在一定的时间中或者是一定的状态下连续的变化.这一类问题常常作为压轴题来考查，学生在“恒定量”的思维惯性下常常找不到解题的思路.解答此类问题最常用的方法就是微元法，本文结合几道例题谈谈如何利用微元法解答高中物理问题.

【关键词】高中物理；微元法；恒定量

微元法的内涵就是将所要研究的物体或者运动过程分割成无限小块，而在这无限小块内，物理量可以看做是恒定的.这时就可以先利用已学知识计算这一小块内所求物理量的大小，之后再综合起来，即可求得总的大小，得到问题的答案，这就是微元法的解题思路.下面用三个典型例题阐述微元法的应用.

类型1 时间元

对于物理量随时间连续变化的问题，一般利用微元法来构造出时间元，在每一小段时间内对物理过程进行研究.

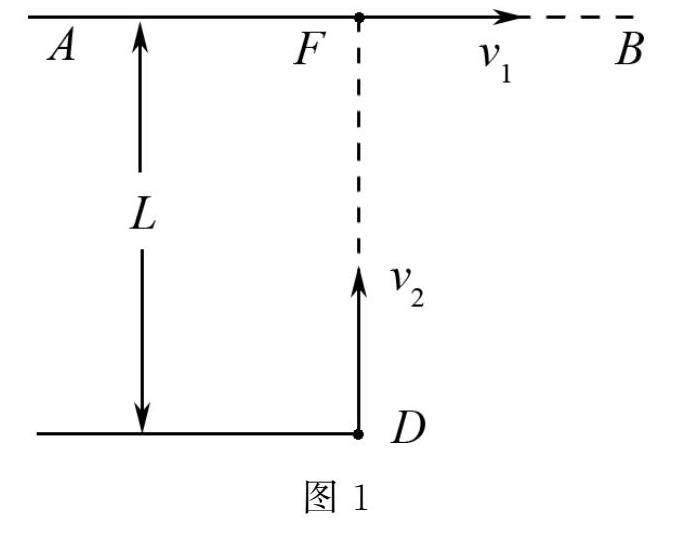
例1 草原上有一只羊被狼追逐，羊以恒定的速度v1沿着直线AB逃跑，狼则以恒定的速率v2追击，狼的速度方向始终对准着羊.已知在某一时刻羊在草原上的F处，狼在草原上的D处，且FD⊥AB，如图1所示，求出此时狼的加速度大小.

解虽然狼在做匀速率运动，但是FD⊥AB，其速度的方向在不断的变化，因此其加速度方向也在不断的变化.

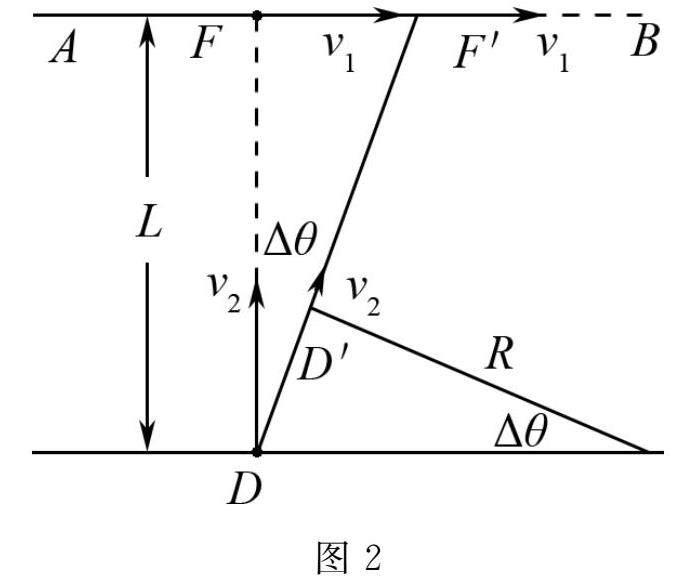
从所求的时刻开始的一段很小的时间（Δt→0）内，结合图2，狼的运动轨迹可近似看做是一段圆弧（其本质上是一条条很小的线段，但是因为Δt→0，就可以看做是圆弧，此处运用了微元法）.

设圆弧的半径为R，则可得狼的加速度a=v22R.在Δt时间内，设羊和狼分别到达了点F′和D′，则此时狼的速度方向转过的角度Δθ=v2ΔtR，而羊在这段时间里跑过的距离是v1Δt=LΔθ.

联立上述两式可得v2ΔtR=v1ΔtL，故可得R=v2v1L，所以代入公式a=v22R可得a=v1v2L.

评析此题的解答过程与求解做匀速圆周运动的物体的向心加速度的過程相类似.将无数个很小的时间内的直线运动合成为圆弧运动是解答物理问题的一个常用方法，在解答此题时就可以转化为圆周运动问题来求解.运用相关的公式，代入即可解得物理量的大小.

类型2 质量元

对于质量连续变化的问题，微元法的使用对象是微小的质量元.并且由于此质量元很小，其它物理效应可以忽略，所以可以看成质点来研究.

例2 某粮店为了方便顾客买米，购买了一个自动称米机，如图3所示.但是细心的顾客认为在称米的过程中容器底部会受到米流落下来所带来的冲力的影响，导致实际的米量与称上的数值并不相同；而卖家则反对，并认为当顾客所需的米量满足时，仍然有一部分米在空中下落，并没有对称造成影响，这些米相当于送给了顾客.双方因为这个问题争执不下，那么哪一方才是正确的呢？

解设米的流量恒定为Q，米流在出口处的速度可以看做是零，不计空气阻力.

自动称米机能够在出口处立即切断米流，使其不再下落.若切断后，装米的容器内的米的总质量为m1，正在空气中下落的米的质量为m2，设落到容器内米堆上的一小部分米的质量为Δm.

在Δt时间内可知Δm=QΔt.以Δm为研究对象，设其落到米堆上之前的速度大小为v，经过Δt时间，其变为静止状态.如图4所示，Δm受到两个力的作用，即其本身的重力Δmg和米堆对其的支持力F.

对此过程使用动量定理可得：（F－Δmg）Δt=Δmv，

即F=ΔmΔtv+Δmg=Qv+QgΔt.

设米在空中运动的时间为t，则m2=Qt，v=gt，故Qv=m2g，F=m2g+Δmg.

设F′为反作用力，根据牛顿第三定律，则称米机的读数应为：

M=Ng=（m2g+F′）g=m1+m2+Δm.

可见，称米机的读数包含了容器中静止的米的质量，也包含了刚落到容器中米的质量，还有在空中下落的米的质量，所以其读数是准确的，双方的说法都是错误的.

评析由此题可以看出，将质量元看做是一个质点，同样可以使用物理定律来研究其与其它物体的关系，之后再将质量元合成即可得到总质量与物体的关系.

类型3 电荷元

在电磁学中微元法将原本总的电荷变成多个连续分布的小电荷，或者是在电荷增加或者减小的连续变化过程中构造电荷元.