微元法生成SPWM的算法研究与实现

2015-06-01范云飞等

软件导刊 2015年5期

范云飞等

摘要：提出用微元法生成SPWM的算法。采用微积分学中微元法这一原理，将基波分割成有限数量的微元。基于采样控制理论，使用等周期、不同占空比的PWM对每项微元等效替代，将其产生的SPWM通过低通滤波器形成所需基波。与现有成熟的SPWM算法进行了对比，讨论了其优点和创新点部分，并推理论证；基于Msp430f169处理器，给出使用MATLAB产生正弦表的程序，对其提出了改进方案。

关键词：逆变技术；SPWM；采样控制理论；微元法；MATLAB

中图分类号：TP312

文献标识码：A 文章编号：1672-7800（2015）005-0062-03

作者简介：范云飞（1993-），男，四川南充人，四川理工学院自动化与电子信息学院学生，研究方向为图像处理、智能控制、工业嵌入式；通讯作者：任小洪（1960-），男，四川南充人，四川理工学院自动化与电子信息学院教授、硕士生导师，研究方向为智能测控技术、无线传感网络技术。

0 引言

逆变技术作为非常重要的一门技术，主要应用于电气火车、变频电源、数控机床、光伏并网、燃料电池静置式发电站等领域。早期逆变主要采用模拟电路实现，精度差，不易进行幅值校正与相位匹配，现在常用微处理器生成SPWM方法。目前行业内成熟的逆变SPWM算法很多，较为常用的有对称规则采样法、不对称规则采样法、等效面积法等，其共性问题是原理复杂、程序繁琐、不易理解，初级学者不易上手。本文基于采样控制理论，提出用微元法生成SPWM的算法，在原理复杂度与程序结构上均有较大改进，更适合中低端单片机进行逆变控制。

1 微元法

1.1 微元法原理

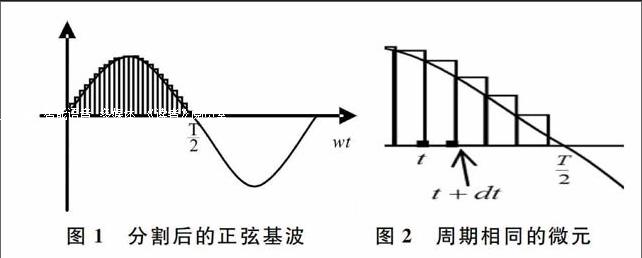
令所要产生的正弦波峰值为1，PWM峰值也为1，将要产生的正弦基波进行有限项切割，见图1。计算每项微元对应的函数值，即对应三角函数值，用与微元项周期相同的PWM波对应一组微元项，见图2，则每项微元所对应的函数值是其对应PWM的占空比。在误差范围内，每项微元对应的占空比产生的一系列PWM波即为所需的SPWM波形。

1.2 原理论证

取直流电压幅值为1，所需的正弦波幅值为1，任取正弦基波时刻t（正半周期内），则表明SPWM每一微元项的占空比为sinωt。令微元频率为F，则微元周期为1F。在周期t至t+1F内，此SPWM所对应的冲量为1F·1·sinωt。由定积分原理可知：

由采样控制理论可知，冲量相等而形状不同的窄脉冲加在具有惯性的环节上时，其效果基本相同。所以，原题设得证。

为了SPWM输出经过积分电路后获得一个较为精确的正弦波，输出SPWM波形中的PWM周期应该远远小于积分电路的积分常数τ[2]。而PWM周期过小，则所需的计算量大大增加，造成系统性能降低，且不能明显提高精度[3]。

2 实验论证

2.1 不规则采样实验

以Msp430f169为处理器，基波频率为F，半周期内有限微元数量为N，则基波周期为：

T=1F（6）

微元周期（载波周期）为：

dt=T2·N=12·N·F（7）

则SPWM中，每项微元周期dt对应占空比η为：

η=sin（2·π·t2N），t=0，1，2，3…，N-1（8）

用定时器A和比较器产生SPWM波，表1中数据是将基波周期定为25HZ，载波周期定为32KHZ所产生的正弦数值表，在单片机中用等周期中断查表修改生成与PWM有关的寄存器TACCRx，即可产生SPWM波。

2.2 微元法实验

以Msp430f169为处理器，使用微元算法生成正弦表，见式（7）、式（8），将基波周期定为25HZ，PWM周期定为32KHZ，用MATLAB仿真，其MATLAB源代码如下：

MainFreq = 8 ；F = 25 ；N = 320 ； t = 0 ：N-1 ；

TACCR0 = round（MainFreq *1000000/（ F *N*2））

data=sin（pi/N*t）*（ MainFreq *1000000/（ F *N*2））；

data=round（data）

微元法产生的正弦表同不对称规则采样法产生的表相同。将此微元法生成的正弦表导入Msp420f169进行查表生成SPWM，其生成的双通道SPWM通过示波器显示如图3所示，显示了基波的正半周逆变波形和负半周逆变波形。

将生成的两路SPWM分别通入低通滤波器，即有如图4的波形。

所以，将生成的SPWM驱动相应桥路后通过低通滤波器即可生成所需正弦波，即完成正弦逆变。

2.3 算法对比

上述实验数据表明，在中低端处理器中不能体现算法的精度，原因是中低端单片机自身的系统误差，具体体现在：①中低端处理器系统时钟较低；②自身输出PWM的分辨率跟不上算法精度。同时，精度高的算法较此微分法运行时间长，表明微元法具有一定优势。

因为自然采样法在计算SPWM波的脉宽时要解超越方程，所以在实际控制中不能保证时效性。对称规则采样法、不对称规则采样法均有使用正弦调制波与三角载波相交原理，其中具有复杂的几何运算，且其使用的正弦调制波与三角载波相交原理在初学时不易明白和掌握，同时，其逆变算法不易从特殊推广到一般。本文提出的基于微元法的SPWM算法只需将对应时间的函数值转化为输出PWM的占空比即可产生SPWM，对比之下，此算法具有原理通俗易懂、算法简单、易于推广的优点，适合逆变初学者。

3 算法改进

处理器不易计算三角函数，若此方法用在DSP等高速处理器上，可直接将MATLAB程序转译为DSP代码。若用于单片机等低速处理器，可将三角函数进行傅立叶展开，取前几项，在精度可接受的情况下，也可粗略控制逆变电路。三角函数傅立叶变换等式[5]为：

sin（t）=t-t33！+t55！-t77！+…（9）

当取前3项时，等效变换为：

sin（t）≈t-t33！+t55！（10）

此时，繁琐的三角函数被化为简单的多项式，简化程度可观。

4 结语

本文提出了用微元法生成SPWM，诠释了数字芯片处理模糊量的经典方法，此法用微积分学理念解释了SPWM原理，其原理相比现有成熟的SPWM算法简单通俗，适合初学者参考，也适合研究人员参考。

参考文献：

[1] 熊军华，王亭岭，陈建明，等.三种SPWM形生成算法的分析与实现[J].微计算机信息，2008，24（7）：307-309.

[2] 沈建华，杨艳琴，翟骁曙.MSP430系列16位超低功耗单片机原理与应用[M].北京：清华大学出版社，2004.

[3] 胡寿松.自动控制原理[M].第5版.北京：科学出版社，2007.