基于深度学习的概念课教学
2024-05-14李成玉
李成玉
在新课标、新教材、新高考的“三新”背景下,课堂教学模式的优化显得更加重要.构建以学生的学为中心的课堂教学模式,从学生学的角度来设计“学历案”,从教材入手,剖析实质,挖掘内涵,深度学习,这更加符合人本主义学习理论,充分体现了高中数学课堂教学中以教师为主导、学生为主体的教学原则,合理构建起“教”与“学”之间的桥梁,还学生课堂的主体地位,给深度学习提供更加肥沃的土壤.
特别地,涉及数学中的概念课教学,合理依托“学历案”的创设,有针对性地进行设计,对于概念的深层理解与拓展应用更加自然,联系并拓展数学知识与实际应用,成为“三新”背景下深度学习的一种基本常态.
1 深度学习的基本思维
1.1 概念内涵的深层理解
基于数学概念课堂的教学实践与深度学习,不仅仅只是停留在数学概念的表层,而是要有效挖掘概念的应用场景与来龙去脉,合理联系概念的本质内涵关联概念的外延,全面构建概念的知识结构与网络链接等,进而更深层次地理解与掌握数学概念,为数学概念的掌握、应用等奠定基础.
1.2 数学思维的深层应用
基于数学概念课堂的教学实践与深度学习,结合数学概念的深入学习,形成良好的数学知识,而這关键的一点,就是构建更加完善与全面的数学思维.借助深度学习,通过构造、类比、联系、创新等思维方式,加深对数学知识的理解与掌握,提升数学思维能力,形成数学习惯,为构建良好的数学思维品质与良好的学科核心素养提供条件.
1.3 创新应用的深层拓展
基于数学概念课堂的教学实践与深度学习,由数学概念到数学知识,由数学知识到数学思维,由数学思维到数学能力,层层递进,为数学创新意识与创新应用埋下伏笔.基于深度学习,可以更加有效把握“四基”,提升“四能”,从而形成更加完善与系统的知识网络体系与框架,对于数学应用与创新应用等方面的提升与拓展都有帮助.
2 深度学习的教学实践
下面以“3.1.1函数的概念”为例(大体安排1课时),通过合理教学设计,基于概念教学,进行教学创设,推进深度学习.
2.1 导学聚焦
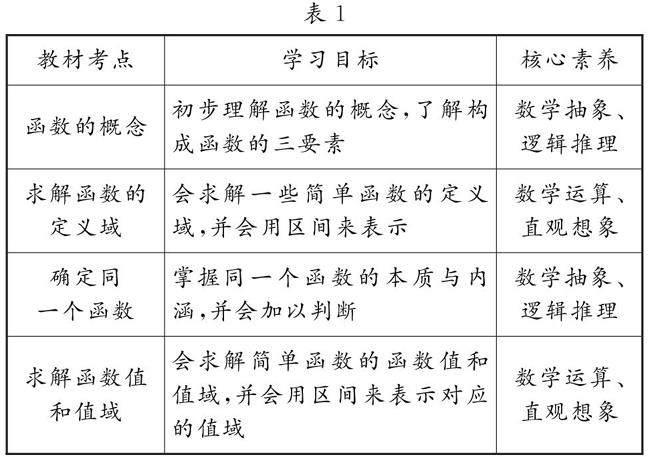
导学聚焦如表1所示.
2.2 自主学习
预习必修第一册第60页~66页第三章“函数的概念与性质”的内容,并带着以下相应的问题来思考与学习:
(1)[JP4]函数的定义是什么?构成函数的三要素是什么?
(2)函数的自变量、定义域是如何定义的?函数的定义域必须满足哪些条件?
(3)函数的值域是如何定义的?函数的值域是由哪些方面确定的?
(4)区间的概念是什么?如何用区间表示对应的数集?
2.3 新知初探
2.3.1 函数的有关概念
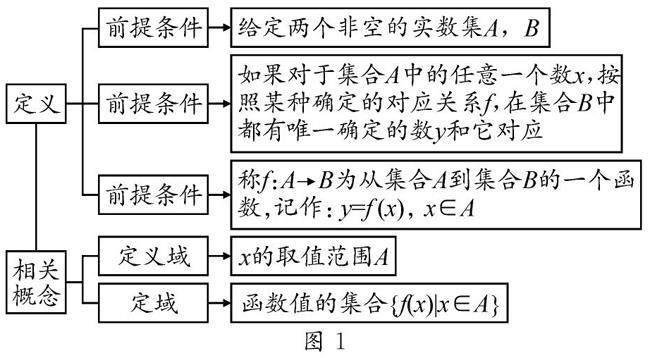
函数的定义及其相关概念如图1所示.
微思考1:(1)函数概念中的集合A和集合B有什么特点?
(提示:A,B为非空数集,集合A中的元素具有任意性,集合B中的数具有唯一性.)
(2)对应关系f一定是解析式吗?
(提示:不一定.对应关系f可以是解析式、图象、表格或文字描述等形式.)
(3)f(x)与f(a)有何区别与联系?
(提示:f(a)表示当x=a时,函数f(x)的值,是一个常量,而f(x)是以x为自变量的函数,一般情况下,它是一个变量,f(a)是f(x)的一个特殊值.)
2.3.2 区间的概念及其表示
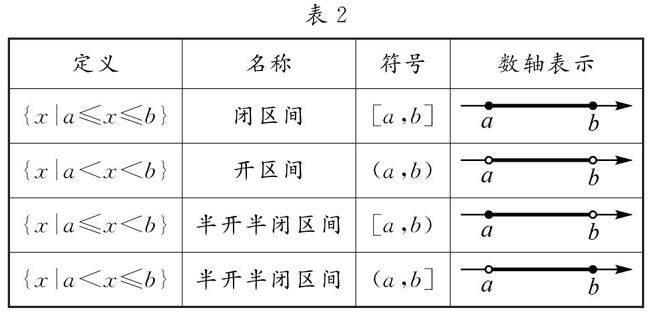
(1)区间定义及表示
设a,b是两个实数,而且a 微思考2:(1)区间是数集的另一种表示方法,那么任何数集都能用区间表示吗? (提示:不是任何数集都能用区间表示,如集合{0}就不能用区间表示.) (2)“∞”是数吗?以“-∞”或“+∞”作为区间一端时,这一端可以是中括号吗? (提示:“∞”读作“无穷大”,是一个符号,不是数.以“-∞”或“+∞”作为区间一端时,这一端必须是小括号.) 2.4 讲练互动 2.4.1 探究点1——函数的概念 例1 如图2中可作为函数y=f(x)的图象的是( ).(D) 设计意图:回归概念,实例剖析,合理归纳总结.(1)判断所给的对应关系是否为函数的方法.先观察两个数集A,B是否非空,再验证对应关系下,集合A中x的任意性,集合B中y的唯一性. (2)根据图形判断对应关系是否为函数的步骤——①任取一条垂直于x轴的直线l.②在定义域内平行移动直线l.③若l与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数. 2.4.2 探究点2——求解函数的定义域 例2 求下列函数的定义域: (1)y=(x+1)2x+1-1-x; (2)y=3-x|x|-5. 答案:(1){x|x≤1且x≠-1}; (2){x|x≤3且x≠-5}. 设计意图:借助实例,归纳总结求解函数定义域时的注意事项.若f(x)含分式,则应考虑分母不为零;若f(x)含偶次根式,则被开方数大于或等于零;若f(x)是由几个式子构成的,则函数的定义域是使几个部分都有意义的自变量x的集合;若f(x)是实际问题的解析式,则应符合实际问题,使实际问题有意义. 3 深度学习的教学启示 3.1 立足课堂,夯实“四基”,深度融合 基于数学概念课堂的教学实践与深度学习,脚踏实地,从立足课堂教学做起,从数学概念抓起,合理深度学习,更加全面有效地把握概念的实质与内涵,有效夯实“四基”,为概念的进一步把握与应用奠定基础,有效提升概念学习的深度与维度,形成数学知识之间的深度融合,有效构建更加合理、完善的数学知识体系. 3.2 把握实质,提升“四能”,深度创新 基于数学概念课堂的教学实践与深度学习,从把握数学实质做起,从数学概念抓起,合理深度学习,更加有效地落实概念的理解与应用,有效提升“四能”,从而合理联系不同知识点之间的联系与应用,拓展数学中不同维度知识的实质,为创新意识与创新应用的养成提供场所,进而更加合理有效地把握数学学科中的基本概念、基础知识、思维方法等的内核与精髓,为深度创新与应用奠定基础. 基于此,以“学历案”的编写与设计,以数学概念的课堂教学进行深度学习,由数学概念到数学知识,由数学知识到数学思维,由数学思维到数学能力,合理“串点成线、织网铺面”,构建一个更加完善的数学知识网络体系,从而全面夯实学生的“四基”,培养学生的“四能”,增强学生的创新意识与创新应用,培育学生的理性思维,促进学生高阶思维和核心素养的全面发展.
