发挥信息技术优势 提升课堂教学效果

吴久辉

摘要：新课程改革的进一步深入，对高中数学的教学手段、教学方式等提出了全新的要求.将信息技术与高中数学教学相结合既能满足学生的发展需求，也符合新课改的要求，在发展学生思维、培养学生的创新意识、提升教学质量等方面发挥着重要的作用.本文中展示了几何画板在高中数学教学中的优势，以期通过适时、适度、适当的应用，提升课堂教学效果，实现学生的可持续发展.

关键词：信息技术；几何画板；教学效果

数学是一门比较抽象的学科，有些内容仅凭教师单方面的讲授学生很难理解和掌握.基于此，在高中数学教学中，教师有必要更新教学方式和教学手段，将抽象的内容生动、直观地呈现出来，这样既易于学生理解和掌握，又可以调动学生参与的积极性，有利于深度学习的达成.而将信息技术与数学教学相结合，可以将知识系统、直观地呈现出来，有效淡化数学知识的抽象感，使数学课堂丰富起来、生动起来，切实提升课堂教学效果［1］.在“直线和圆的位置关系”教学中，笔者借助几何画板，将圆与直线的位置关系形象、直观、准确地呈现出来，在帮助学生理解知识的同时，激发学生学习兴趣，提升学生数学思维能力和数学核心素养.现结合具体案例，谈谈几何画板的教学优势.

1 巧借几何直观，促进理解

解析几何既是教学重点，也是教学难点，许多学生在学习这部分内容时容易产生畏难情绪，从而影响最终学习效果.确实，对于初学解析几何的高一新生来讲，这部分内容比较抽象，涉及层面较广，综合应用比较灵活，仅凭教师讲授很难让学生将相关知识、方法等学懂、吃透.在实际教学中，为了让学生更加直观地感悟直线与圆的位置关系，大多教师会渗透数形结合思想，以期借助形的直观淡化问题的抽象性，帮助学生克服畏难情绪，提高学生参与课堂的积极性.在具体实施过程中，教师若选择课上手工绘图，这样不仅会浪费宝贵的课堂时间，而且难以准确表达蕴含其中的数学关系.而利用几何画板可以有效解决以上问题，快速、直观、准确地呈现图形，更易于学生理解和掌握.

案例1 中点轨迹问题

教学中，教师设计了如下几个问题：

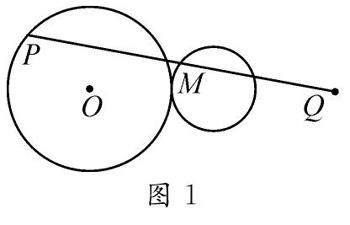
（1）已知P是定圆O上一动点，Q为圆O外一定点，连接PQ，M是PQ的中点，当P在圆O上运动时，点M的轨迹是什么？

（2）已知P是定圆O上一动点，点Q在过圆心O的定直线上，且线段PQ为定长，M是PQ的中点，当点P在圆O上运动时，点M的轨迹又是什么？

（3）在平面直角坐标系xOy中，P，Q分别为y轴和x轴上的两动点，且线段PQ为定长，M是PQ的中点，当动点P在y轴上运动时，M的轨迹又是什么？

教学中，教师先让学生思考并提出自己的猜想，然后运用几何画板进行动态演示，让学生借助图形进一步观察（如图1～图3），帮助学生加深对中点轨迹问题的理解.

通过直观演示可以轻松得到如下结论：问题（1）中，中点M的运动轨迹是圆；问题（2）中，中点M的运动轨迹是椭圆；问题（3）中，中点M的运动轨迹是圆.

这样借助几何画板就将中点轨迹的三个问题直观、快速、准确地呈现出来了.通过经历以上过程，学生可以感受轨迹的产生过程，有利于培养空间意识，提升直观想象素养.另外，通过动态展示，抽象的问题会变得更加直观、简洁、生动，便于理解和掌握.通过经历以上过程，还可以帮助学生积累丰富的活动经验，有利于发展学生的数学思维和核心素养.

2 借助直观精准，促进发现

直线与圆相结合的图形运动问题是高考的一个重要考点，该类型的题目比较抽象，具有一定难度.在日常教学中，若教师仅是就题论题式的讲授，将影响学生知识体系的建构，不利于学生解决问题能力的提升.因此在实际教学中，教师不妨借助多媒体的直观化、系统化、精准化，引导学生对相关知识进行归纳总结，让学生的脑海中形成清晰的知识脉络，从而提高迁移水平[2].

对于两个非同心圆的一般方程，若将两圆的一般方程作差，则得到一个二元一次方程，即一条直线l的方程.该直线与已知两圆可能会有一定的特殊的关系，这是一个值得探究的问题.两圆的位置关系有多种，受其影响，直线l与两圆的特定关系也会有所不同.这种不同很难单纯地靠说或板书来表达，教学中可着重演示这一动态变化过程，引导学生在变化中逐渐抽象概括，从而发现规律.在具体实施过程中，教师不妨借助几何画板来动态演示，引导学生通过观察、抽象概括等过程，提高教学实效性.

案例2 直线和两圆的位置与方程的关系

教学中，教师以两圆相交这一位置关系为引例，开启探究之旅：

问题 如图4，作两相交圆圆O1和圆O2，其交点为M，N，令点M，N所在直线为l，在直线l上取一点P（异于点M，N），过点P分别作圆O1和圆O2的切线PE，PF，连接O1O2.结合图形，说说你有何发现？

学生通过直观观察易于发现：（1）在直线l上任取一点作两圆的切线，则切线长相等；（2）直线l与两圆的连心线垂直.基于以上发现，教师让学生度量两圆及直线的方程，观察、猜想并验证它们之间的关系.猜想及证明过程如下：

猜想：若圆O1和圆O2相交，则直线l的几何意义是两圆的公共弦所在的直线.

证明：设P1（x1，y1），P2（x2，y2）是两圆的交点，则有x21+y21+D1x1+E1y1+F1=0和x21+y21+D2x1+E2y1+F2=0成立，即P1（x1，y1）滿足方程（x21+y21+D2x1+E2y1+F2）－（x21+y21+D1x1+E1y1+F1）=0，整理得（D1－D2）x+（E1－E2）y+F1－F2=0.同理，P2（x2，y2）也满足上式.所以直线l表示两圆的公共弦所在的直线.

在此基础上，教师让学生继续思考：两圆相离、相切或内含时，是否有符合以上条件的直线l？这样借助几何画板的直观、快速、准确，打开了学生的思维大门，让学生对蕴含于图形中的一些特殊结论了然于心，有利于提升学生学习信心，发展学生数学核心素养.

3 提供实践机会，提升素养

几何画板是研究几何问题的重要工具，可以将抽象的知识和复杂的问题直观地展示出来，从而为知识的理解和问题的解决提供便利.在现实教学中，几何画板以教师操作为主，这样虽然高效，但是学生的思路被教师牵着走，学生的发现局限于教师的预设中，影响学生创新意识的培养.在实际教学中，教师可以提供机会让学生自己操作，这样既可以调动学生参与的积极性，又能激活学生的思维，提高学生的动手探究能力和创造力.在课堂教学中，只有真正将主动权交给学生，才能充分释放学生的无限潜能，提升学习品质和教学有效性[3].

案例3 和两个定圆相切的动圆圆心轨迹

如图5，已知两定圆O1和O2的半径分别为r1，r2，动圆M与两圆相外切.

（1）如果两定圆相离，那么圆心M的轨迹是什么？

（2）如果两定圆外切，情况会怎样？

（3）如果两定圆相交、内含、内切，又能得到怎样的结论？

（4）如果两定圆内切于动圆M，圆心M的轨迹又会怎样呢？

对于以上问题，若直接让学生推理分析，容易滋生学生的畏难情绪，因此教师不妨提供机会让学生动手实践探究，让学生通过操作、观察、分析、归纳等活动轻松地解决问题.另外，通过动手实践探究形成的直观认识，会给后续的推理验证提供助力，有利于学生发现、分析和解决问题能力的提升.

事实证明，适度地将几何画板等多媒体技术应用于数学教学实践中，可以使抽象、枯燥的数学知识变得形象、直观、生动，可以有效激发学生学习兴趣，从而让学生的学变得更加积极、主动.值得注意的是，在实际操作中，教师切勿独揽课堂，要提供机会让学生去操作、去发现，这对学生提高自主探究能力、发展直观想象素养、提升数学思维能力等都是极其有益的.同时，教学中要提供机会让学生去合作、交流，让学生充分体会绘图的乐趣以及体验发现的喜悦，充分激发学生的主体性和主动性，促进学生数学核心素养的落实.

总之，几何畫板作为优质的教学软件，操作简单，功能强大，将其应用于教学能发挥传统教学无法比拟的作用.在实际教学中，教师要适时、适度、适当地加以应用，充分发挥其直观、生动、快捷等优势，加快新知内化进程，助力学生全面提升.

参考文献：

［1］闵启蒙.几何画板在高中数学教学中的应用策略[J].当代家庭教育，2020（7）：97.

［2］刘卫富.高中数学运用《几何画板》辅助解题的探究[J].数理化解题研究，2020（3）：28-29.

［3］黄山.信息技术环境下的三角函数教学——浅谈几何画板在教学中的运用[J].考试周刊，2019（47）：86-87.