以“圆锥曲线”教学为例谈数形结合思想的渗透

闻君

摘要：数形结合既是一种数学思想方法，也是一种解题策略，是沟通数与形的桥梁，连接具体与抽象的纽带.本文中以“圆锥曲线”相关内容的教学为例，充分展示了数形结合在加强基础知识理解、提高学生解题能力、发展学生数学思维能力和数学能力等方面的优势，以期在日常教学中，通过合理有效的渗透，实现个体认知结构的优化和解题能力的提升，促进学生的全面发展.

关键词：数形结合；思维能力；数学能力

数形结合将抽象思维转化为形象思维，从而实现抽象、复杂问题直观化、形象化，凸显数学本质，促进学生分析和解决问题能力的提升[1].数形结合实现了“数”与“形”相互沟通，其为数学学习提供方向，有利于数学能力和数学素养的发展与提升.

“圆锥曲线”既是高中数学的重点，也是教学难点，还是高考的考点，其在高中数学教学中的地位和价值是不言而喻的.在“圆锥曲线”教学中，教师中应该重视渗透“数形结合”思想，以此借助图形的形象、直观激发学生的学习兴趣，加深相关知识的理解，帮助学生突破教学的重难点，提高学生应用相关知识解决问题的能力.那么在圆锥曲线教学中，如何发挥数形结合思想方法的优势，以助学生更好地把握知识，提高教学有效性呢？以下笔者结合自己的教学经验谈几点粗浅的认识，供参考！

1 巧借数形结合，促进知识理解

高中范围内圆锥曲线主要包括椭圆、双曲线和抛物线这三大板块，这三大板块的内容具有一定的抽象性和相似性.在日常教学中，若教师直接呈现相关概念、结论等让学生熟记，很容易造成混淆，从而影响解题效果和学习信心.基于此，在研究定义、性质等相关内容时，教师不妨渗透数形结合思想，以此充分发挥图形直观的优势，帮助学生在脑海中形成清晰的知识脉络，建构完善的知识体系[2].

例如，在学习“椭圆”的定义时，为了让学生更好地理解椭圆的定义，教师可以先引导学生将文字语言转化为符号语言——|MF1|+|MF2|=2a（其中|F1F2|<2a），在此基础上，借助图形来观察△MF1F2，并引导学生利用“三角形的三边关系”去理解定义，以此加深对“|F1F2|<2a”的理解.学习了双曲线的定义后，教师可以用同样的方式让学生理解，为什么定义中强调“|F1F2|>2a”.这样通过文字语言、符号语言和图形语言的相互转化，学生脑海中有了图形和定义，日后在研究圆锥曲线的标准方程时，自然可以借助图形获得等量关系，从而轻松地实现由“形”到“数”的转化，增强学习信心.

又如，在教学“拋物线的定义”时，教师可以利用几何画板进行演示，让学生体会“数随形动”，借助几何直观获得其中的数量关系，得到抛物线的定义.这样借助形使抛物线的定义更加生动形象，更易于学生理解和掌握，以便学生建立关于抛物线的图形和数量关系的知识体系，为数学知识的应用打下坚实的基础.

2 巧借数形结合，直观把握性质

在日常教学中发现，学生能够快速地求出圆锥曲线的标准方程，但是在描述各量之间的关系，并用蕴含其中的数量关系解决问题时，部分学生常感无从下手.究其原因就是学生的脑海中并未建立直观图形，这样学生在表述其中蕴含的数量关系时就显得缺乏逻辑性和层次感.基于此，教学中，教师若能借助图形将其中蕴含的数量关系直观地表示出来，定能达到事半功倍的效果.

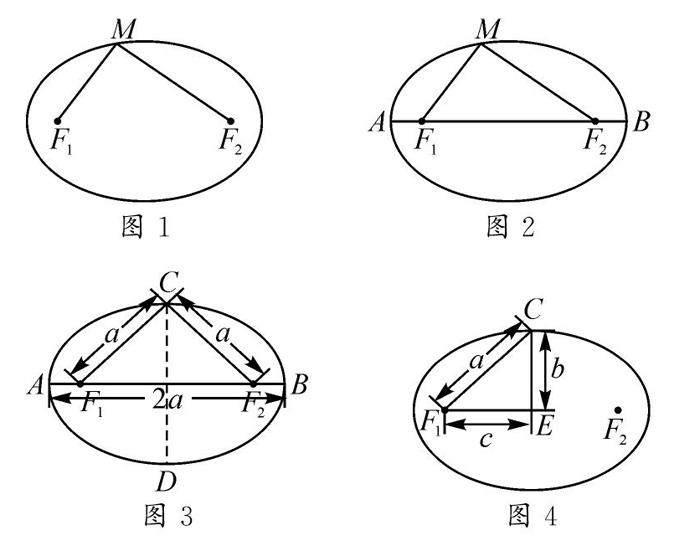
例如，椭圆标准方程中引入a，b，c三个量，教学中教师不仅要让学生知道相关的量分别代表的几何意义，还要提供机会让学生去提炼其中的等量关系.在实际教学中，为了让学生更好地把握知识，教师给出图1～4所示的图形让学生观察、抽象.如对于图1，M是椭圆上一点，F1，F2为椭圆的焦点，则有|MF1|+|MF2|=2a；对于图2，若椭圆的长轴端点分别为A，B，F1，而F2为椭圆左、右焦点，则|AF1|+|AF2|=|AF1|+|BF1|=2a；对于图3，若椭圆短轴端点是C，D，则|CF1|+|CF2|=2a，|CF1|=|CF2|=a；对于图4，结合勾股定理，易得a2=b2+c2.这样借助图形的直观可以帮助学生更好地理解其中蕴含的数量关系，从而为解题带来便利.

又如，学习了“抛物线的性质”后，教师给出了这样一道题：抛物线y=4x2的焦点坐标是[CD#3].该题是一个基础题，但是解题效果并未达到预期，部分学生因误认为2p=4，所以得到了（1，0）这一错解.对于这一错误，若教师给出抛物线标准方程让学生观察、套用，学生虽然能够获得正解，但是这样的教学缺少了一定的探究性，难以诱发学生的深层思考.基于此，教师不妨引导学生将方程转化为x2=14y，并画图.让学生借助图形去观察、去体会，从而使问题迎刃而解.在日常教学中，当学生解题过程中出现一些模棱两可的情况时，教师可以引导学生去画图，直观观察、理解，以此消除困惑，提高学习信心.

再如，有这样一道问题：方程（x+3）2+y2+（x－3）2+y2=10表示什么？问题给出后，先让学生独立求解.从解题反馈来看，学生看到该方程就联想到两点间的距离公式，从而得到的结论是：平面内一点（x，y）到（－3，0）和（3，0）两点的距离之和为10.显然从代数角度分析还不够具体、形象，需要从几何角度进一步抽象：平面内一点到两定点的距离之和为常数，且该常数大于两定点间的距离，根据椭圆的定义可知，该点的轨迹是椭圆.学生通过分析知晓该点的轨迹是椭圆后，教师可以预留时间让学生画出椭圆，并写出a，b，c的值.这样，通过数与形的相互转化，顺利地得出该方程表示焦点在x轴上的椭圆，其标准方程为x225+y216=1.

学习了圆锥曲线的相关性质后，教师不要急于让学生去记忆，应该尝试引导学生借助图形去分析、去抽象、去感悟，这样可以使圆锥曲线的性质更加直观、形象，以此帮助学生直观化地把握性质，有效提高解题效率和解题准确率.

3 巧借数形结合，将几何问题代数化

在学习数学的过程中，既要借助形的直观来理解数，也要用数的严谨分析形，通过形与数的相互转化，形成正确的解题思路，提升学生分析和解决问题的能力.

例如，直线与圆锥曲线的位置关系是高考的一个重要考点.在研究位置关系时，若仅从形的角度去观察，显然不具说服力，为此在研究位置关系时，需要将几何问题代数化，运用代数知识来解决.在研究位置关系时，教师可以鼓励学生联想研究圆与直线位置关系的方法，利用方程思想解决问题，通过判断一元二次方程的实根个数，确定圆锥曲线与直线的位置关系.

在学习的过程中，教师要有意识地引导学生进行新旧知识的类比，通过新与旧的有效沟通，提高学生自主探究能力，帮助学生建构完善的体系.

4 巧借数形结合，拓展数学思维

数与形是相互联系的有机整体，二者相互补充，密不可分.在研究圆锥曲线中的数量关系和几何关系时，教师要有意识地引导学生将二者有效地联系在一起，通过彼此的相互转化实现化抽象为具体、化无形为有形，帮助学生快速地形成解题策略，提高解题效率[3].

例如，学习了双曲线相关知识后，教师给出了这样一道练习：已知双曲线x29k2－y24k2=1与圆x2+y2=1没有交点，求实数k的取值范围.从解题反馈来看，学生看到“交点”二字，首先想到的就是利用方程思想解决问题，将两方程联立，通過消元将其转化为一元二次方程，根据Δ<0，得到不等式，从而通过解不等式，求得k的取值范围.该思路是合理的，但是解题过程中涉及复杂的运算，这样不仅会占用较多的解题时间，而且容易出现错解的风险.基于此，不妨换个角度，将代数问题几何化，借助图形的直观寻找解题的突破口.结合已知易得到一个圆心在原点，半径为1的圆，而该圆与焦点在x轴上的双曲线无交点，则说明双曲线的实半轴大于圆的半径，所以由a=9k2=|3k|，可得|3k|>1.显然借助形来分析，问题会变得更加简洁，有效地优化了运算过程，提高了解题效率和解题准确率.

总之，无论是从加深知识理解的角度，还是从提升解题能力的角度来分析，研究圆锥曲线离不开“数”与“形”的相互转化.因此，在日常教学中，教师要将“数形结合”思想方法融于圆锥曲线的课堂教学实践中，让学生充分感知数形结合的应用价值，以此培养数形结合意识，提升学生数学核心素养.

参考文献：

［1］郭文.数形结合思想在高中数学解题中的运用探究[J].科技资讯，2020（10）：237-238.

［2］刘宗明.数形结合思想在高中数学教学中的实践探究[J].数学学习与研究，2019（15）：31.

［3］赖敏.数形结合简析，分步突破细化——以圆锥曲线问题的突破为例[J].数学教学通讯，2021（6）：79-80，88.