回归教材重基础 精研真题提素养
2024-05-14严振君
严振君
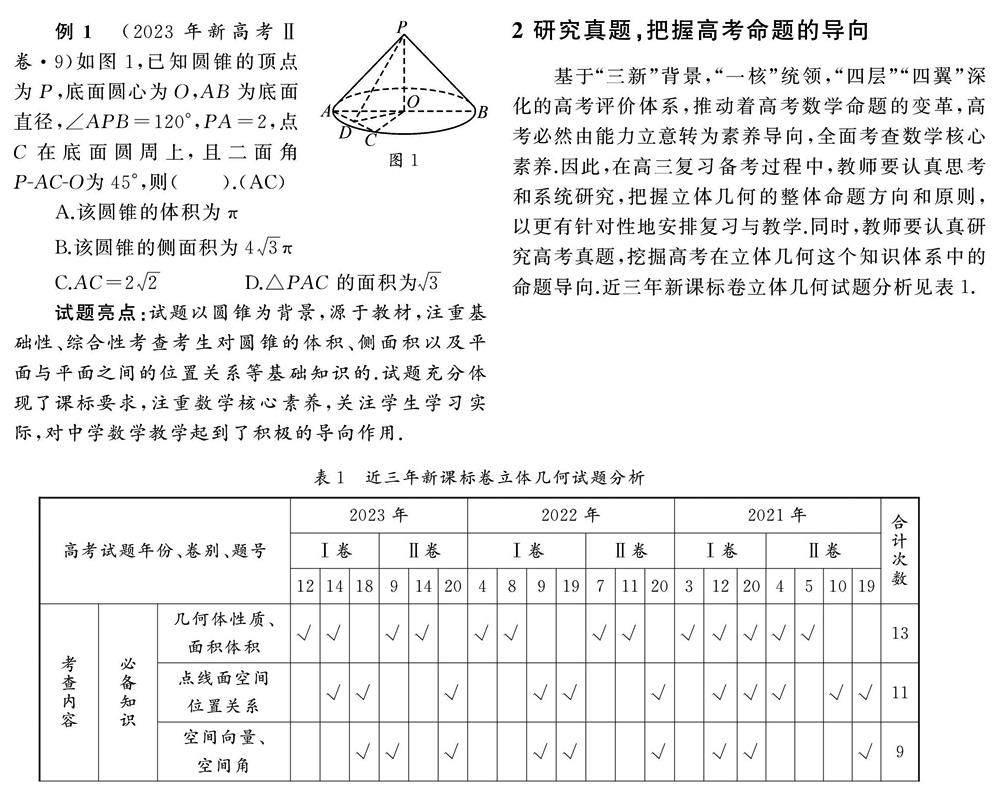

高考立体几何试题的“四基”切入,落实对学生及数学基本能力、数学核心素养等方面的考查.基于此,新课标下的立体几何的复习备考应该更加灵活、全面.
1 回归教材,建立完整的知识体系
高中数学教材是全面落实数学课程体系的重要载体,是落实课程目标以及培养学生数学核心素养的重要教学资源.同时,教材中的一些典型例(习)题、相关栏目等,也是历年高考数学命题的一个重要素材.
教师可以有针对性地对一些典型例(习)题、教材中重要公式和定理的推导过程与推导方法等加以拓展与探究,帮助学生建立完整的知识体系.
1.1 熟悉教材,抓住知识点的联系
在回归教材时,梳理数学知识间联系、探寻基本思想和方法的脉胳,主要是通过教材中的典型例(习)题,以及一些特殊栏目,阅读、探究等,从这些问题中挖掘素材,包括蕴含其中的数学思想方法,合理拓展相关知识,开阔学生的视野,发散学生的思维,提炼出通性通法,准确把握数学知识的本质与数学能力的要点.
1.2 挖掘教材,寻觅高考题的“影子”
教材的内容具有其他数学教学参考书、练习卷等教辅所不可替代的作用和教育教学功能.回归教材,挖掘教材,引导学生深入领会教材中对应例(习)题、相关栏目等典型问题中所展示出来的专家学者的命题意图,并加以研究和开发,合理追根溯源.这样处理不但可以丰富教学内容,还可以就地取材,减少所谓的[LL]“补充内容”,减少资料书的使用,从而更好地从高考真题中寻觅其“影踪”,提升教材的综合应用与拓展空间.
试题亮点:[HTK]试题以圆锥为背景,源于教材,注重基础性、综合性考查考生对圆锥的体积、侧面积以及平面与平面之间的位置关系等基础知识的.试题充分体现了课标要求,注重数学核心素养,关注学生学习实际,对中学数学教学起到了积极的导向作用.
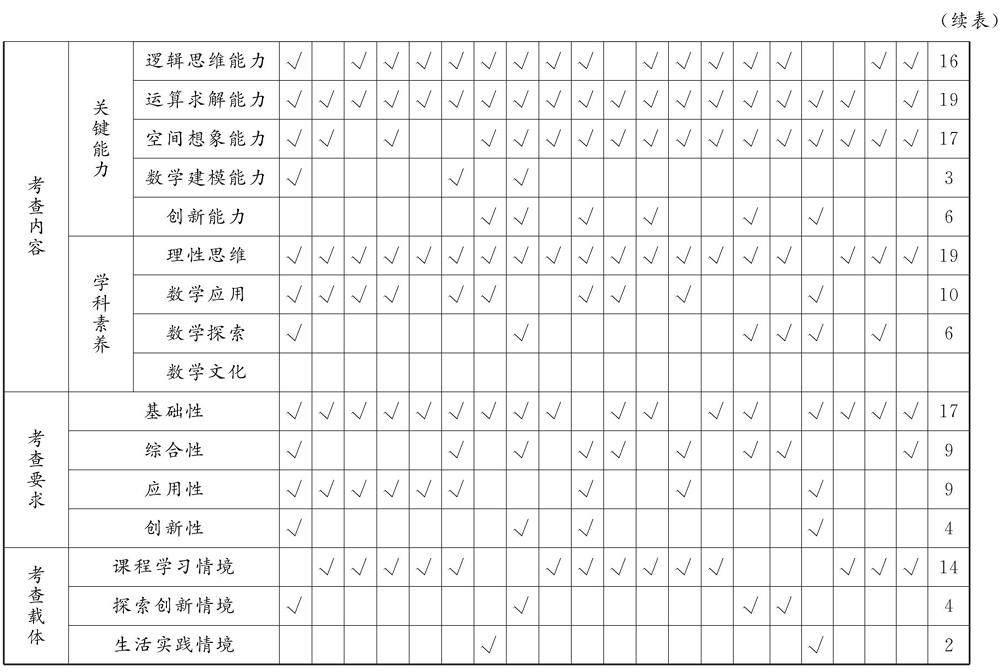
2 研究真题,把握高考命题的导向
基于“三新”背景,“一核”统领,“四层”“四翼”深化的高考评价体系,推动着高考数学命题的变革,高考必然由能力立意转为素养导向,全面考查数学核心素养.因此,
在高三复习备考过程中,教师要认真思考和系统研究,把握立体几何的整体命题方向和原则,以更有针对性地安排复习与教学.同时,教师要认真研究高考真题,挖掘高考在立体几何这个知识体系中的命题导向.
近三年新课标卷立体几何试题分析见表1.
試题亮点:试题以正四棱锥和球设置探索创新情境.试题的正确运算基于空间想象,同时还需要依靠严密的逻辑推理,才能发现空间几何体中相关量之间的关系,进而完成对问题的求解.试题在考查立体几何基础知识、基本方法的同时,考查考生空间想象、逻辑推理以及数学运算等关键能力和几何体的构图能力.
3 夯实基础,提升应考的基本能力
高考对立体几何的基本能力的要求:
(1)理解并记忆空间几何体涉及到的公式、公理、性质定理与判定定理,并熟练掌握每一个公理或定理的作用;学会画图,能够构建符合题目要求的图形,以便快速找到内在联系.
(2)熟练掌握基本模型(切、接模型,正方体模型,长方体模型,在长方体的8个顶点中任取四个构成的三棱锥模型,外接球模型);掌握垂直、平行问题的一般处理方法,特别是怎样作辅助线;掌握空间角的基本概念,能利用几何法(定义法)处理简单的空间角问题;掌握利用向量法解决空间几何体问题的一般方法和书写格式;注意解三角形与平面几何知识在解题中的应用等.
4 抓住本质,培养解题的核心素养
教师在教学中可以抓住立体几何中“形”的几何本质,从几何法思维切入加以空间想象与直观分析,结合逻辑推理与数学运算等深入培养数学抽象、直观想象、逻辑推理等核心素养;也可以抓住立体几何中“数”的代数属性,从向量法思维切入加以代数运算与逻辑推理,从而以空间向量的形式巧妙数学运算,达到数学运算与逻辑推理相结合的目的.
在复习备考阶段,教师要合理引导并鼓励学生在解题时多采用一些基本方法来分析与处理,特别在解决立体几何的解答题时,可以灵活选用几何法与向量法等不同方法,多思维角度来分析与应用,引导学生的思维活动,凸显问题本质.
从近年高考立体几何试题的分析不难得出,立体几何考查的主要内容还是基于常规、熟悉、简单的空间几何体,借助这些空间几何体来考查相关的数学基础知识与基本能力等.在复习过程中,教师要特别注重解题的通性通法的教学.
