Top-k空间偏好查询方法研究

2024-05-10鲍金玲张志威

长春师范大学学报 2024年4期

田春,鲍金玲,张志威,刘刚

(1.吉林化工学院信息与控制工程学院,吉林省吉林市 132000;2.白城师范学院计算机科学学院,吉林白城 137000)

0 引言

随着无线通信技术的快速发展和移动通信设备的不断普及,基于位置服务的应用越来越广泛,查询要求也越来越复杂,比如Top-k空间关键字偏好查询[1-5]和Top-k空间偏好查询[6-13]。

Top-k空间关键字偏好查询是指在查询中考虑查询对象周围的空间属性和文本属性是否满足用户的查询需求,返回前k个最优的空间对象。例如,一位游客计划在北京预订一个周围有饭店的宾馆,希望获得周围1公里内饭店评价等级最高的前k个宾馆排名列表,并且这些饭店都能提供“西餐和停车场”,然后从中选择自己满意的宾馆。而Top-k空间偏好查询是根据空间对象周围的特征对空间对象进行等级评价,返回k个最佳对象的排序列表。例如,一位游客计划在北京预订一个周围有饭店和超市的宾馆,希望获得周围1公里内饭店和超市评价等级最高的前k个宾馆排名列表,然后从中选择自己满意的宾馆。在上述Top-k空间关键字偏好查询和Top-k空间偏好查询中,宾馆是游客感兴趣的设施,超市和饭店是游客关注的周边设施,“周围1公里”是游客提出的空间约束条件,“西餐和停车场”是饭店的文本约束条件。两者最主要的区别在于Top-k空间偏好查询不考虑空间对象中的文本属性。

在实际生活中,Top-k空间偏好查询的应用很广泛,可以应用在地理信息系统、城市建设规划、资源调度与分配、旅游规划等领域。近年来,国内外很多大学和研究机构对Top-k空间偏好查询展开了深入研究,并取得了许多有价值的研究成果。本文对欧式空间和路网环境下的Top-k空间偏好查询方法进行研究,分析和总结现有方法的优点和不足。

1 问题描述

定义1 数据对象指用户感兴趣的设施类型,例如上述查询实例中的“宾馆”。数据对象集用D表示,p表示数据对象集D中的一个对象点。

定义 2 特征对象指用户关注的周边设施类型,例如上述查询实例中的“超市和饭店”。特征对象集用F表示,f表示特征对象集中的一个对象。

定义3 特征对象分数指用户对特征对象的评级,用符号w(f)表示。每个特征对象的分数被归一化为[0,1]范围内的数值。

定义5 将路网结构表示为一个图结构G=(V,E,W),其中V表示路网路段中的交叉节点集合,E表示路网中路段集合,每条边分配一个有向或无向的方向,W表示路段对应的权重,这里表示该路段的长度。

定义6 路网距离指从查询点到查询对象的最短路径长度,用l(ni,nj)表示,其中ni表示起点,nj表示终点。

定义7 Top-k空间偏好查询是指给定一个数据对象集D{p1,…,pn}和m个特征对象集F1,…,Fm,查询Q(D,F,θ,k)就是根据数据对象周围满足约束条件的特征对象得分来计算数据对象点的得分,返回得分最高的k个数据对象点,具体表示为:

(1)

当θ表示范围约束时,Top-k空间偏好范围约束查询是指在数据对象集D中,查找r范围内各类特征对象集Fi分数和最高的前k个数据对象点。对于每一类特征对象集,数据对象p的第i个分量范围得分是指r范围内特征对象f∈Fi的最高得分,具体表示为:

(2)

当θ表示最近邻约束时,Top-k空间偏好最近邻约束查询是指在数据对象集D中,查找最近的各类特征对象集Fi分数和最高的前k个数据对象点。对于每一类特征对象集,数据对象p的第i个分量最近邻得分是指最近特征对象f∈Fi的最高得分,具体表示为:

(3)

当θ表示为影响力约束时,Top-k空间偏好影响力约束查询是指在数据对象集D中,查找各类特征对象集Fi中对象的分数与权重的乘积,以及其和最大的前k个数据对象点。r是用户指定的空间范围,数据对象集D与特征对象f之间的距离越近,特征对象f的影响力分数越高。数据对象p的第i个分量影响力约束得分具体表示为:

(4)

在欧式空间中,r指的是欧式距离,d(p,f)表示数据对象p与特征对象f的直线距离;路网环境中r指的是路网距离,l(p,f)表示数据对象点p与特征对象f的路网距离。

对象点欧式空间分布如图1所示,横轴与纵轴刻度值表示距离。从图1可读取对象点的坐标,例如,p1的坐标为(0.5,4)。假设用户查询为Q1(D,(F1,F2),θ,2),其中k=2,D={p1,p2,p3}。a、b表示两类不同的特征对象。F1={〈a1,0.7〉〈a2,0.8〉〈a3,0.5〉〈a4,0.3〉〈a5,0.7〉},F2={〈b1,0.8〉〈b2,0.6〉〈b3,0.6〉〈b4,0.4〉}。数据对象集D={p1,p2,p3}代表“宾馆”,用实心三角形表示;特征对象集F1={a1,a2,a3,a4,a5}代表“饭店”,用实心矩形表示;特征对象集F2={b1,b2,b3,b4}代表“超市”,用空心矩形表示。特征对象后边的数字表示特征对象的等级分数,分数一般来源于用户的评级,归一化为[0,1]范围内的数值。

图1 欧式空间查询示例图

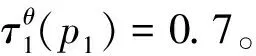
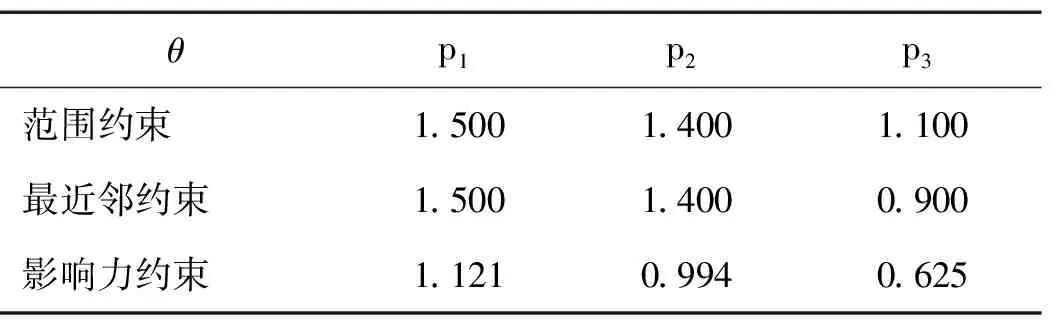
表1 数据对象p1,p2,p3得分

将图1按照路网中的状态抽象为图结构G=(V,E,W),如图2所示,V表示路网中的交叉节点集合v1,…,v9;E表示路网中的相连节点的边集合;W表示边的权重,在此表示节点之间的路网距离,表示边上的数字,例如l(v1,p1)=0.5,l(p1,a1)=1数据对象集D={p1,p2,p3}代表“宾馆”,用实心三角形表示;a和b表示两类不同的特征对象,特征对象集F1={a1,a2,a3,a4,a5}代表“饭店”,用实心矩形表示;特征对象集F2={b1,b2,b3,b4}代表“超市”,用空心矩形表示,括号中的数值表示特征对象的分数。

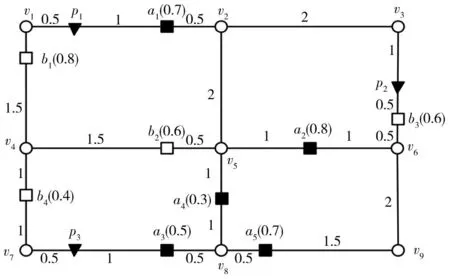
图2 无向路网环境查询实例图

根据图2,在路网环境中,用户查询为Q2(D,(F1,F2),θ,2),分别处理范围约束、最近邻约束和影响力约束下的Top-k空间偏好查询。这与欧式空间查询要求相近,不同之处是所有距离均为路网距离。根据三种约束查询的要求,可得出数据对象p1,p2,p3的得分表,如表2所示,其中数据对象p1,p2为查询结果。

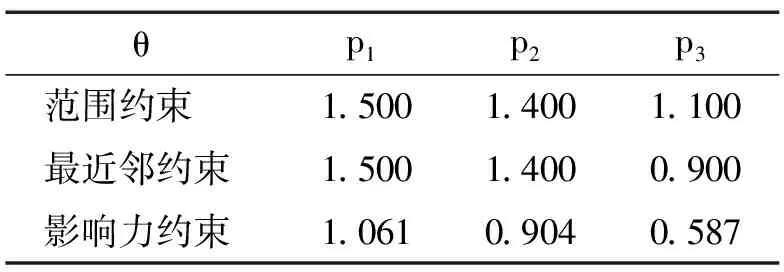
表2 数据对象p1,p2,p3得分表

2 欧式空间中的Top-k空间偏好查询方法

根据空间索引结构,本文将查询方法划分为两类:基于R-tree索引结构的查询方法[6-8]和基于网格索引结构的查询方法[9-10]。

2.1 基于R-tree索引结构的Top-k空间偏好查询方法

R-tree是Guttman在1984年提出的一种动态空间索引结构,用来访问二维或者更高维区域对象组成的空间数据。基于R-tree索引,YIU等[6]提出了SP算法、GP算法、BB算法和FJ算法,解决范围与最近邻约束下的Top-k空间偏好查询。在上述工作基础上,YIU等[7]将算法扩展到影响力约束下的Top-k空间偏好查询,并对BB算法做出改进,提出了BB*算法。ROCHA等[8]基于R-tree索引提出了SFA算法,解决范围约束、最近邻约束和影响力约束下的Top-k空间偏好查询。

2.1.1 SP算法

SP算法采用R-tree索引数据对象点和MAX aR-tree索引特征对象点。以查询Q1(D,(F1,F2),θ,2)为例,首先,利用R-tree对图1中数据对象点构建索引,如图3所示,假定每个节点限定子节点个数为3,位置上相邻的结点尽量在树中聚集为一个父结点,叶子节点e2中存储包含数据对象p1,p2最小外接矩形的坐标和数据对象p1,p2的唯一标识符,e3中存储数据对象p3的最小外接矩形的坐标和数据对象p3的唯一标识符,根节点e1中存储能够覆盖子节点e2,e3区域的最小外接矩形和指向子节点e2,e3的指针。然后,利用MAX aR-tree索引特征对象点,如图4所示,叶子节点中存储包含特征对象最小外接矩形的坐标以及特征对象的唯一标识符,非叶节点中存储覆盖所有子节点区域最小外接矩形坐标、子结点中特征对象分数的最大值以及指向子节点的指针。

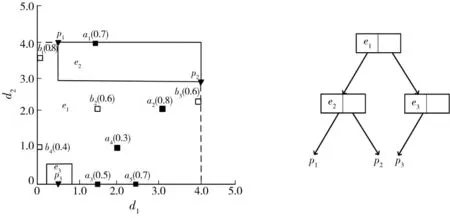
(a)空间区域划分 (b)R-tree示例图

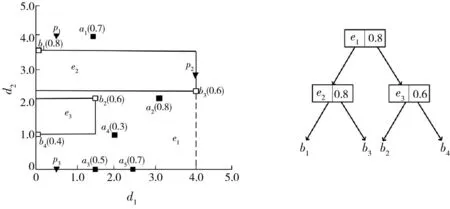
(c)F2中对象点的区域划分 (d)R-tree示例图

SP算法的基本思想是通过计算每个数据对象点的得分来检索查询结果。为了提高算法效率,通过数据对象的得分上界进行剪枝。在SP算法中使用两个全局变量wk和γ,其中wk存储得分最高的k个数据对象点的信息,γ是wk中的最低分,τ+(p)是数据对象得分的上界。在遍历一个特征对象树时,得到当前已知数据对象的分量得分τc(p),其余没有遍历的特征对象树,对应的数据对象的得分上界设置为1。此时可以得出数据对象得分的上界τ+(p)为已知的分量分数之和。当一个数据对象上限分数不大于γ时,该数据对象被剪枝;而数据对象点的实际分数大于γ时,更新wk和γ。

由SP算法的基本思想可知,当数据对象规模增大时,SP算法效率会明显降低,而k增大时,SP算法的查询效率基本不受影响。

2.1.2 GP算法

为了提高Top-k空间偏好查询的效率,文献[6-7]在SP算法的基础上提出了GP算法。GP算法与SP算法不同的是,当访问数据对象树的一个叶子节点时,将叶子节点中所有对象节点存储在一个集合中,然后在遍历特征对象树的过程中同时计算它们的分数。GP算法的查询效率略高于SP算法,k增大时,GP算法的查询基本不受影响。

2.1.3 BB算法

BB算法是在GP算法剪枝策略的基础上,利用数据对象树中所有非叶项的上界T+(e)对数据对象点进行剪枝。在满足空间约束的特征对象树中,最低级别的非叶项e存储子树中特征分数的最大值,由此可以计算出目前已知的数据对象树中非叶项的分量分数Tc(e),而未知的数据对象树中非叶项的上界设置为1。

此时上界T+(e)为已知的分量分数之和。如果数据对象树中非叶项的上界T+(e)<γ,对该非叶项的子树中包含的数据对象点进行剪枝。当数据对象树中的非叶项的上界T+(e)≥γ时,展开非叶项的子树,求所包含的数据对象点的得分。

(a)F1中对象点的空间区域划分 (b)R-tree示例图

运用BB算法计算数据对象树中非叶项的上界,对无效数据对象点进行剪枝。当数据对象和特征对象规模增大时,BB算法效率明显优于GP算法和SP算法,而k增大时,BB算法的查询效率基本不受影响。

2.1.4 BB*算法

BB算法中,当数据对象和数据对象树非叶项的分量分数为未知的情况时,数据对象得分的上界τ+(p) 和数据对象树中非叶项的上界T+(e)都设置为分量得分的最大取值1,两个上界均不够紧致,所以剪枝效果不理想。为了增强以上两个上界的紧致性,加强剪枝效果,BB*算法[7]利用一个大顶堆按照特征对象树中的特征分数降序遍历每类特征树中的数据项,通过从堆中弹出来的特征对象分数来计算数据对象的得分。数据对象的分量得分τc(p)为当前访问的特征对象树对应的大顶堆弹出的得分,该数据对象其余分量的得分上界不会大于从对应的特征对象大顶堆中最后弹出的分数,这使得上界τc(p)更加紧致。计算数据对象树非叶项的上界T+(e)时,逐一访问特征对象树中最低级别的非叶项e,获取每个非叶项子树中特征分数的最大值,得到更加紧致数据对象树非叶项的上界T+(e)。当数据对象规模和特征对象规模增大时,BB*算法的效率明显优于前面的三个算法,而k增大时,BB*算法的查询效率同样不受影响。

2.1.5 FJ算法

FJ算法[6-7]的主要思想是对特征对象树进行多路空间连接,逐一检索数据对象点附近满足空间约束的特征对象组合,并将特征对象组合按照总分数进行降序排序,然后按照排序顺序检索数据对象点。FJ算法结合了特征树的非叶项,对那些总分数小于已查询到的第k个数据对象点的分数的特征对象组合,以及不能满足空间约束的特征对象组合进行剪枝。如果得分最高的特征对象组合的所有项都是叶子节点,则检索其空间邻域中的数据对象点,否则展开得分最高的非叶项。FJ算法受特征对象种类的数目影响最大,当特征对象的类别较少时,FJ算法的性能要优于SP、GP、BB和BB*算法,在特征对象类别为2的情况下,效率最佳;而特征对象种类增多时,需要检索的特征组合数目呈指数级增长,查询效率明显降低。当k增大时,FJ算法的剪枝能力减弱,查询效率明显降低。

2.1.6 SFA算法

SFA算法[8]将数据对象和特征对象映射到距离-分数空间,在距离-分数空间中横坐标表示距离,纵坐标表示等级分数。算法根据距离-分数支配关系过滤无效的映射对,得到不同约束下Top-k空间偏好查询所需要的Skyline集,然后利用R-tree索引Skyline集,聚合从每个R-tree中检索到的数据对象的分量分数,最终返回前k个Top-k空间偏好查询的结果。

查询实例1,Q1(D,(F1,F2),θ,2),SFA算法根据图1中的对象点,利用R-tree对Skyline集建立索引,如图5所示。数据对象p1到特征对象集F1={a1,a2,a3,a4,a5}的距离分别为d(p1,a1)=1,d(p1,a2)=3.20,d(p1,a3)=4.123,d(p1,a4)=3.35,特征对象集F1中对象的分数分别为w(a1)=0.7,w(a2)=0.8,w(a3)=0.5,w(a4)=0.3,w(a5)=0.7,所以数据对象p1与特征对象集F1映射到距离-分数空间的坐标分别为(p1,a1)=(1,0.7),(p1,a2)=(3.2,0.7),(p1,a3)=(4.123,0.5),(p1,a4)=(3.35,0.3),(p1,a5)=(4.47,0.7)。同理可得到其余的数据对象和特征对象对的映射坐标。根据支配关系得到Skyline集,利用R-tree索引Skyline集,Skyline集为S1{(p1,a1),(p2,a2),(p1,a2),(p3,a2)(p3,a3),(p3,a5)(p2,b3),},S2{(p1,b1),(p2,b1),(p3,b1), (p3,b2),(p3,b4)}。

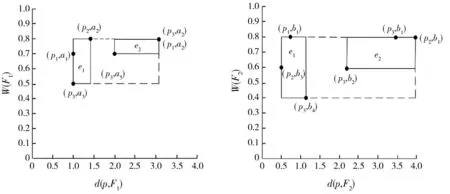
(a)根据S1建立的R-tree (b)根据S2建立的R-tree

SFA算法可以扩展到大规模数据集,算法的查询效率比较稳定。当数据对象和特征对象规模增大时,SFA算法效率明显优于上述其他算法,k增大时SFA算法的查询效率基本不受影响。

2.2 基于网格索引结构的Top-k空间偏好查询方法

网格索引通过对地理空间进行网格划分,将查询区域划分成大小相等或不等的网格,建立一个倒排文件——栅格索引,每一个网格在栅格索引中有一个索引记录,在这个记录中标记所有位于或穿过该网格的对象。孙焕良[9]和刘俊岭[10]采用网格索引结构解决Top-k空间偏好查询。

文献[9-10]利用网格索引二维空间的数据,结合概念划分的剪枝策略,分别针对范围约束和最近邻约束下的Top-k空间偏好查询提出了TopRNG-G算法和TopNN-G算法。根据图1中的对象点创建网格索引,如图6所示,每个网格对应着一块存储空间,存储对象点的信息。

(a)欧式空间查询示例图 (b)网格划分

TopRNG-G算法主要结合概念划分的思想,利用网格到查询对象点的距离进行剪枝,当该距离大于范围距离r时,对网格内所有点进行剪枝。TopNN-G算法定义一个距离的全局变量,存储查询点到已找到的最近邻特征对象的最远距离,利用概念划分思想将查询点周围的单元格合并成概念矩形,然后根据查询点到概念矩形的最小距离进行剪枝,当该距离大于当前最佳距离时,则对网格内的所有点进行剪枝。

当特征对象规模增大和特征对象种类增多时,TopNN-G算法和TopRNG-G算法查询效率优于FJ算法,当k增大时,利用网格索引的算法与利用R-tree索引的算法基本都不受影响。

2.3 欧式空间Top-k空间偏好查询方法总结

基于R-tree索引的SP、GP、BB、BB*、FJ和SFA六种算法均支持范围约束、最近邻约束和影响力约束的Top-k空间偏好查询,基于网格索引的TopNN-G算法和TopRNG-G算法分别支持最近邻约束和范围约束下的Top-k空间偏好查询。综合现有研究,对以上八种算法查询性能进行比较与分析,SFA算法的查询效率明显优于其他算法。具体情况如表3所示,分别考虑数据对象规模、特征对象规模、查询的特征对象种类和k的变化情况对算法性能的影响,可知,当数据对象规模增大时,FJ算法查询效率所受影响最小,GP算法所受影响最大,查询效率明显降低;当特征对象规模增大时,SFA算法的查询效率所受影响最小,GP算法的查询效率所受影响最大;当查询的特征对象种类增多时,FJ算法的查询效率所受影响最大,SFA算法的查询效率所受影响最小;当k增大时,FJ算法的查询效率所受影响最大,SFA算法的查询效率所受影响最小,而BB*、TopNN-G和TopRNG-G算法对于上述参数变化,查询效率所受影响较小。

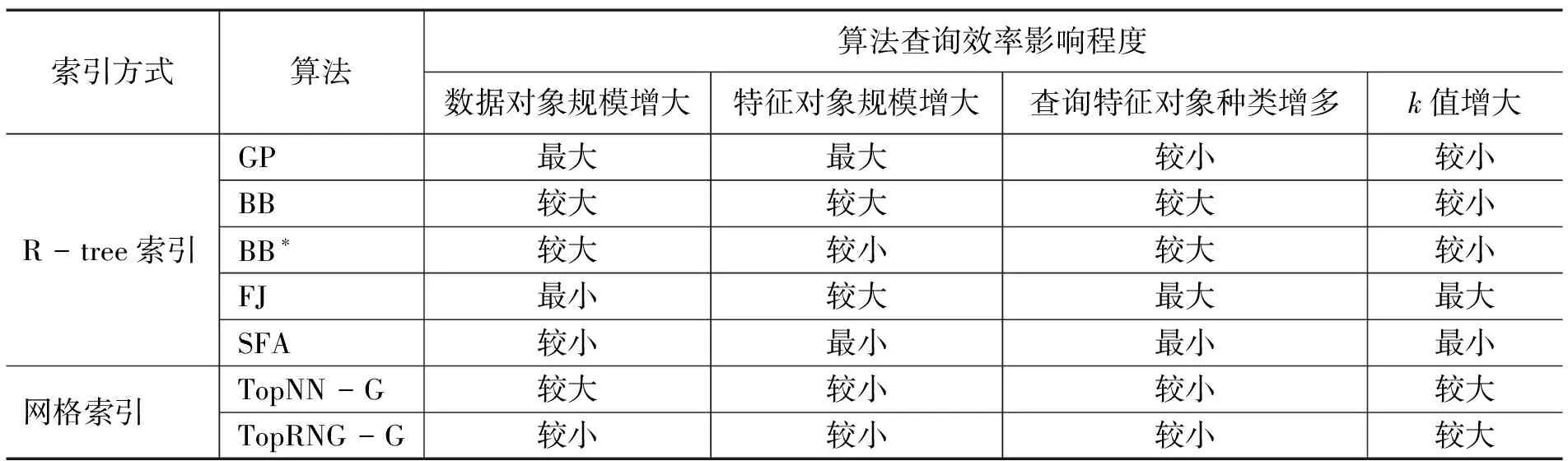
表3 算法查询效率分析表

3 路网环境下Top-k空间偏好查询方法

路网环境下Top-k空间偏好查询更贴近日常生活,目前也取得一定的研究进展。根据路网特征,本文将查询方法划分为无向路网和有向路网两类,即无向路网环境下Top-k空间偏好查询方法[11]和有向路网环境下Top-k空间偏好查询方法[12-13]。

PAPADIAS等[14]提出了INE算法和RNE算法,实现路网环境下的k近邻查询。通过对INE算法的改进,可以解决有向与无向路网环境下最近邻和影响力约束的Top-k空间偏好查询。通过对RNE算法进行改进,可以解决有向与无向路网环境的范围约束下的Top-k空间偏好查询。

3.1 无向路网环境Top-k空间偏好查询方法

CHO等[11]针对无向路网环境下Top-k空间偏好查询提出了ALPS算法。该算法预计算路网中所有交叉节点的最短路径表,然后将任意两个交叉节点之间包含的数据对象提前划分成数据段,计算每个数据段到每个特征对象点最大和最小距离,再将数据段与每个特征对象点映射到距离-分数空间,其中横坐标表示距离,纵坐标表示等级分数,根据Skyline方法确定数据段和特征对象组对之间的支配关系,过滤掉被支配的数据段或者数据对象点,然后使用一个大顶堆按照数据对象的分量分数降序遍历每个Skyline集,最后基于NRA算法[15]思想将各个堆中弹出的数据对象的分量分数相加,返回得分最高的数据对象。

查询实例2为Q2(D,(F1,F2),θ,2),ALPS算法根据图2中的对象点,利用R-tree对Skyline集建立索引(图7),构造图2中对象点的Skyline集。数据对象p1到特征对象集F1的路网距离分别为l(p1,a1)=1,l(p1,a2)=4.5,l(p1,a3)=5,l(p1,a4)=4.5,l(p1,a5)=6,特征对象集F1中对象的分数分别为w(a1)=0.7,w(a2)=0.8,w(a3)=0.5,w(a4)=0.3,w(a5)=0.7,所以数据对象p1与特征对象集F1映射到距离-分数空间的坐标为p1⊗a1=([1,1],0.7),p1⊗a2=([4.5,4.5],0.8),(p1⊗a3)=([5,5],0.5),(p1⊗a4)=([4.5,4.5],0.3),(p1⊗a5)=([1,1],0.7)。同理可得,其余数据对象和特征对象对映射到距离-分数的坐标。根据数据段和特征对象对在距离-分数空间的支配关系得到Skyline集:S1{(p1⊗a1),(p1⊗a2),(p2⊗a2),(p3⊗a2),(p3⊗a3),(p3⊗a5)},S2{(p1⊗b1),(p2⊗b1),(p2⊗b3)(p3⊗b1),(p3⊗b2),(p3⊗b4)}。

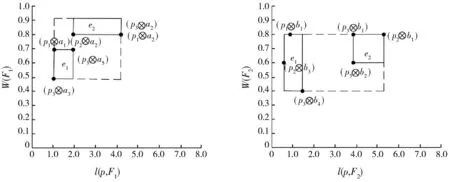
(a)根据S1建立的R-tree (b)根据S2建立的R-tree

3.2 有向路网Top-k空间偏好查询方法

在无向路网环境抽象后的图2中,设置路段方向后,得到有向路网的抽象图,结构如图8所示。ATTIOUE等[12-13]将Top-k空间偏好查询扩展到有向路网,并提出了TOPS算法。TOPS算法的基本思想是预处理节点之间的距离,定义了静态维度、静态等式、静态支配和完全支配,并根据上述特征过滤特征对象。每个特征对象都与一个轴节点相关联,因此将共享同一轴节点的特征对象组合在一起。计算数据对象到特征对象组最大距离和最小距离,将数据对象和特征对象组对映射到距离-分数的二维空间,利用Skyline方法过滤掉被支配的数据对象和特征对象,利用R-tree索引过滤后的Skyline集,使用一个大顶堆按照数据对象的分量分数降序遍历每个Skyline集,然后基于NRA算法[15]思想将各个堆中弹出的数据对象的分量分数相加,返回得分最高的数据对象。

图8 有向路网环境查询实例图

查询实例3为Q2(D,(F1,F2),θ,2)。根据图8中的对象点,利用R-tree对Skyline集建立索引,如图9所示。根据定义的静态维度、静态等式、静态支配和完全支配,得到每个数据对象有用的特征对象:{(p1⊗a1),(p2⊗a1),(p3⊗a1)(p3⊗a2)(p3⊗a3)(p3⊗a5)}{(p1⊗b1)(p2⊗b1)(p2⊗b2)(p2⊗b3)},将数据对象和特征对象组映射到距离-分数空间。根据数据对象和特征对象组对之间的支配关系得到Skyline集:S1{(p1⊗a1),(p1⊗a2),(p2⊗a1)(p2⊗a2),(p3⊗a3),(p3⊗a5)},S2{(p1⊗b1),(p2⊗b1),(p2⊗b3)(p3⊗b1)(p3⊗b2),(p3⊗b4)}。

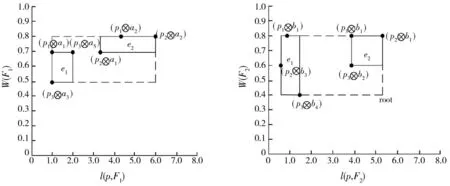
(a)根据S1建立的R-tree (b)根据S2建立的R-tree

3.3 路网环境下Top-k空间偏好查询方法总结

综合现有研究,对无向路网环境和有向路网环境下的Top-k空间偏好查询算法性能进行比较与分析,无向路网环境下,ALPS算法的查询效率明显优于改进的INE算法和改进的RNE算法;有向路网环境下,TOPS算法的查询效率明显优于改进的INE算法和改进的RNE算法。

在无向路网环境下,分别考虑数据对象规模、特征对象规模、查询的特征对象种类和k的变化情况对算法性能的影响,具体情况如表4所示,当数据对象规模和特征对象规模增大时,ALPS算法的查询效率所受影响较小,改进的INE算法和改进的RNE算法的查询效率所受影响较大,查询效率明显降低;当特征对象种类增多时,改进的INE算法和改进的RNE算法查询效率所受影响较小,ALPS算法的查询效率所受影响较大;当k值增大时,改进的INE算法、改进的RNE算法和ALPS算法查询效率所受影响较小。

表4 无向路网环境下R-tree索引各算法查询效率分析表

在有向路网环境下,分别考虑数据对象规模、特征对象规模、查询的特征对象种类和k的变化情况对算法性能的影响,具体情况如表5所示,数据对象规模和特征对象规模增大时,TOPS算法的查询效率所受影响较小,改进的INE算法和改进的RNE算法的查询效率所受影响较大,查询效率明显降低;当查询特征对象种类增多时,TOPS算法的查询效率所受影响较小,改进的INE算法和改进的RNE算法查询效率所受影响较大,查询效率明显降低;当k值增大时,改进的INE算法和改进的RNE算法查询效率所受影响较小,TOPS算法的查询效率所受影响较大。