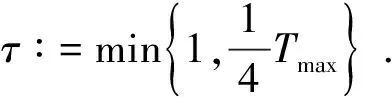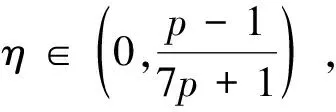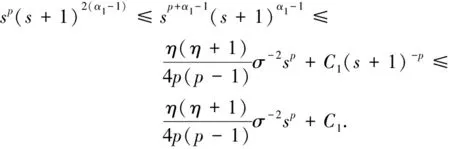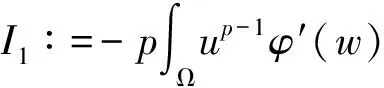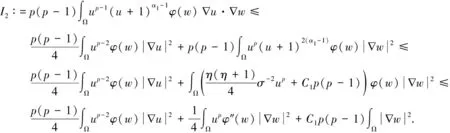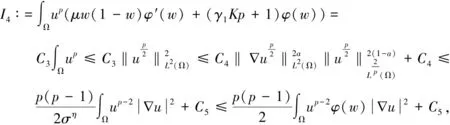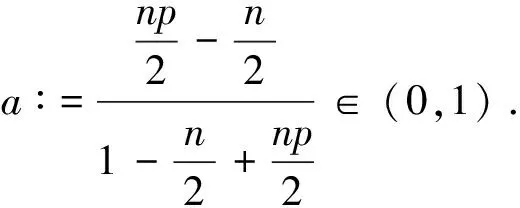带有竞争的非线性捕食者-食饵模型解的有界性

赵司军,王 辉,2

(1.伊犁师范大学数学与统计学院,新疆 伊宁 835000; 2.伊犁师范大学应用数学研究所,新疆 伊宁 835000)

0 引言

在生态系统中,捕食关系被视为生物种群之间最主要的关系之一,是指一个生物种群捕食另一个生物种群以获取所需的能量和营养物质.捕食关系对于生态系统的结构和功能具有重要影响,能够调节生物种群的数量和分布,保持生态系统的平衡和稳定.1987年KAREVIA和ODELL[1]提出了以下模型:

(1)

其中,u(x,t)和w(x,t)分别代表捕食者和食饵的密度.常数d和D分别表示捕食者和食饵的扩散速率,d,D>0;-χ∇·(u∇w)表示捕食者对食饵的趋向性;γ表示从食饵到捕食者的转换率;函数h(u)和f(w)表示种内相互作用,uF(w)表示种间相互作用.

许多学者都对模型(1)进行了研究,得到了模型解的动力学的研究结果,如全局存在性[2-5]、一致有界性[4,6]和渐近行为[6]等.在模型(1)单个捕食者的基础上,也有研究人员考虑了以下双捕食者的情形:

其中,u(x,t)和v(x,t)代表两类捕食者的密度,w(x,t)代表食饵的密度.

ZHENG[7]成功证明了在二维有界区域中模型(2)存在唯一的全局经典解.同时,针对β1=β2=0的情形,ZHENG也研究了模型(2)的常值稳态解的全局渐进稳定性.鉴于自然界中捕食者朝着食饵的运动远不是模型(2)所描述的那么简单,在文献[7]的研究基础之上,本文考虑以下带有竞争机制的非线性捕食者-食饵模型:

定理1假设γ1,γ2,θ1,θ2和μ都是正常数,β1,β2则为非负常数.如果条件:

αi<1,i=1,2

1 预备知识

首先简述一下模型(3)经典解的局部存在性结果.

引理1.1 假设定理1中的条件成立,则存在最大存在时间Tmax∈(0,∞],使得满足:

的唯一的三元函数组(u,v,w)是模型(3)在Ω×(0,Tmax)中的经典解.同时可知,

u(x,t),v(x,t)>0,0

进一步地,若Tmax<+∞,则有

(5)

在证明定理1时,除了局部存在性外,还需要借助以下结论,详细的证明过程可参阅文献[7]和[8].

引理1.2 假设定理1中的条件成立,则对任意t∈(0,Tmax),存在某个常数C>0,使得

2 定理1的证明

从估计模型(3)解的第三个分量w开始讨论.

引理2.1 假设定理1中的条件成立,则存在一个常数C>0,使得对于任意t∈(0,Tmax),有

证明 利用模型(3)中的第三个方程,由Young不等式计算可以得到:

根据u和v的非负性,可以推出:

从而引理2.1得证.

根据引理2.1, 立即得到以下推论.

推论2.1 假设定理1中的条件成立,则存在一个常数C>0,使得对于任意t∈(0,Tmax-τ),有

受到CAO等[9]所使用的试验函数的启发,接下来将使用加权积分的方法来获得Lp有界性.

引理2.2 假设定理1中的条件成立,则对任意p∈(1,∞),对任意t∈(0,Tmax),存在某个常数C>0满足:

和

因为α1<1,利用Young不等式,可以找到常数C1,C2>0,使得对于任意s>0,有下列不等式成立:

(13)

和

(14)

结合(3)中第一个和第三个方程,对任意t∈(0,Tmax),可以得到:

(16)

进一步地,将(16)中右边最后四项分别记作I1,I2,I3,I4.首先,通过Cauchy-Schwarz不等式得到:

再次使用Cauchy-Schwarz不等式,联立(11)和(13)可以得到:

(18)

类似地,联立(11)和(14)可以得到:

(19)

对于I4,记C3∶=μKη+γ1Kp+1,由式(6)、式(11)、Gagliardo-Nirenberg不等式和Young不等式可以推导出,存在常数C4>0和C5>0使得:

(20)

综合上述估计,将(17)～(20)一起代入(16),结合(12),对任意t∈(0,Tmax),可以得到:

(21)

其中,c6∶=C1p(p-1)+pησηC2.

联立引理1.3和推论2.1,对任意t∈(0,Tmax),存在C7>0满足:

根据(11)有φ(w)≥σ-η.在(22)两边同时乘以ση,可以证明(9)成立,其中C∶=σηC7.类似地,也可以证明式(10)成立.至此,引理2.2得证.

定理1的证明在引理2.2结论的基础上,根据抛物方程的正则性理论,对任意t∈(0,Tmax),存在一个常数C>0满足:

‖w(·,t)‖W1,∞(Ω)≤C.

此外,利用Moser-Alikakos迭代技巧[10],对任意t∈(0,Tmax),可以得到:

‖u(·,t)‖L∞(Ω)+‖v(·,t)‖L∞(Ω)≤C,

其中,C也是一个常数,C>0.

结合引理1.1,由此完成了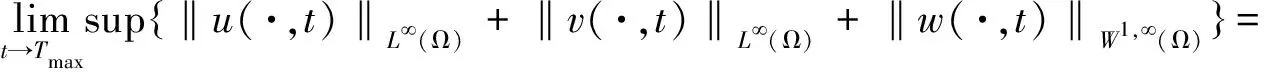定理1的证明.