因惑而思，辨而明之——论小学数学课堂“思辨”教学的策略

江苏省如皋市白蒲小学 孙明霞

“明辨之，笃行之。”“有弗思，思之弗得，弗措也。有弗辨，辨之弗明，弗措也。”思辨是复杂的，受人脑的支配，更与思维密不可分。新课标指出，学生学习应当是一个生动活泼的、主动的和富有个性的过程。除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。显然，相依而生的就是学生思辨能力的发展，即数学思维的发展。今天的课堂要求教师“限时讲授”，为的就是把课堂的“话语权”还给学生，让学生说得自由、清楚，说得有理、精彩！

当然，这对教师的课堂驾驭能力无疑提出了更高的要求。课中的生成点拨，应凌驾于整个课堂之上，教师要有俯瞰课堂的能力。诚然，精彩的、有价值的“思辨”并不是一蹴而就的，尤其是小学生，在学生第一阶段尝试“学走路”的活动中，教师恰如其分的“扶”尤为重要。那么，究竟该如何去“扶”？又该何时“放”呢？

一、分层设疑，有思有辨

在学习活动中，每个学生都是独立的个体，他们有各自的思维方式与并不统一的思维水平。这些需要教师清晰地认识到，且这也是教学中不可逃避的现实。我们无法将学生“拔”成同一高度，却可以顺势而为、因势利导。在教学中，教师应根据学生的实际需要，顺应学生的思维层次，让教学设计本身就有思考的空间，每个学生都能有思考的切入点，给予学习滞后的学生登上更高阶梯的时间与空间。

如在执教“用数对确定位置”一课时，笔者设计了如图1 的活动导学——“数对含义辨析”，给处在不同思维阶段的学生思考的突破口。

图1

活动思辨问题设置了三个层次。其一，对于数感较强，且能很快掌握数对含义的学生来说，他们从第1问就已经直接可以从提供的数对中发现这些数对的第一个数字，即表示列的数相同，由此推理得出A、B、C、D、E五个点在同一列。当然能这样思考出来的学生对数对含义的掌握已很深刻，且已将其内化为自己的理解认知了。他们的抽象思维和逻辑推理能力很强，能较快地发现问题的本质。然而，更多的学生是不能快速内化新知、触摸问题本质的，那么就需要教师给学生一个“垫脚石”，帮助他们通过新的途径解决问题。其二，第2 问中，明确提出让学生仔细观察，一一对比数对中暗含的特点。抽象的数对并不能满足所有学生探究时的发现。于是，有了“小提示”：“可以用笔涂一涂哦！”当学生一个一个找出这些点并依次涂上颜色后，便能一眼看出这些数对所表示的点有何特征与联系。这时，“数形结合”给了学习稍稍滞后的学生发现与思考的机会。这样每个学生都有了自己的思辨，而且这些思辨的角度、程度不一，也就给了他们思维碰撞的机会。愈辨愈晰，愈思愈明，学生慢慢迈向问题本质，如此，思辨的本质是如此惊人的一致！思辨的过程尤为精彩：动笔描点、绘制出数对所在点的位置的学生会有惊奇的发现，乐于与同伴分享自己的作品，并从中描述自己的发现，而这个描点图，也证实了学生对抽象数对规律的发现。如此分层设疑，是高水平的相辅相成，让人人有思，人人可辨！

教师在课堂中看似波澜不惊，实则是不露痕迹地各给所需，让每个学生都有适合自己的垫脚石，使学生在不知不觉中进行思与辨。

二、引“矛”攻“盾”，是辨亦思

“头脑不是一个需要被填满的容器，而是一个需要被点燃的火把。”教师的责任就是用自己的星星之火去点燃学生思辨的火把，在课堂中，将难点变成“矛盾”的激发点，抓住生成，引“矛”攻“盾”，引发“头脑风暴”，在生生的思辨、你来我往中，激发学生的求知欲望，打开学生思维的闸门，让学生进入“心求通而未通，口欲言而未能”的境界。

在执教“可能性”一课时，笔者设计了“猜球”这一活动。教学片段如下：

师：老师给你们准备了三个口袋，一起来看看——（1 号：2 黄、2 绿、2 红。2 号：3 绿。3 号：2 红2 绿）

师：老师昨天在家摸了其中一个袋子里的球，但摸的究竟是几号口袋，记不起来了。我一共摸了4 次，分别是绿球、绿球、绿球、绿球。是几号口袋呢？

（学生兴趣盎然、激烈地猜测着）

师：想想，要摸到绿球，这个袋子里就得放什么球？

生1：袋子里放绿球。

生2：袋子里一定要全都是绿球。

……

课堂中，教师切中肯綮：“想想，要摸到绿球，这个袋子里就得放什么球？”教师适时在趋于平静的思维“湖面”上丢下一颗引发“思辨”的石头，在有价值的分歧点上，一石激起千层浪。教师“四两拨千斤”，以智激智，着意引领。渐渐地，大部分学生开始倾向生1的观点。争辩，亦是思维最好的触媒剂，不同的人会有不同的思考，教师必须尊重学生独特的个性，并使之自由发展。而这样的“头脑风暴”，让学生的思维进入高度活跃期、发散期。一旦学生的思维被激活了，则教学效率显著提高。

三、以“退”为“推”，辨“知”思“质”

诚然，“思辨”的课堂不是一味地高歌猛进，适时的以“退”为进，更是让“思辨”走向深刻。在苏教版数学教材中，不难发现有很多需要学生不断自主探究、发现的活动。如“钉子板上的多边形”“和与积的奇偶性”，这些活动如只是一味地对照表格数据或算式去观察、提出猜想等，无疑是生涩、枯燥的，所谓的小组交流也只是答案的校对，这会降低学生自主探究的积极性。教师可以适时地借助简单、有趣的游戏来刺激学生的好奇心，其实就是以蕴含数学思想的数学游戏等助推学生思考，给学生创设争辩的机会，让他们在“百家争鸣”的探索中产生灵感与动力。

如在教学“钉子板上的多边形”时，教师应用极限思想，开展了这样的游戏活动：

导入部分，给每个学生一张有格点的A4 纸，要求在格点纸上尽可能地画出一个面积最大的图形。

师：来，将自己的作品举起来，相互展示一下！看看，怎样画的图形面积最大？

师（总结）：看来，这图形的面积可能与什么有关？

生1：多边形边上的钉子数。

生2：多边形所包含的钉子数（即多边形内的钉子数）。

……

师（总结）：看来，影响多边形面积的因素很多。我们从简单的入手，先来研究多边形的面积与边上钉子数的关系。（板书：多边形的面积、多边形边上的钉子数）

由此游戏引入探究影响多边形面积的诸多要素，让学生产生“思辨”的必要，而不是生硬地告知。其实，很多自然科学的发现就是人类在不设限的无尽假设中发现、证实的。

在课堂最后，教师再次借助了游戏的形式：

师：这回还是一个比赛，规则有所不同：

比赛规则：在3 号格点纸上，尽可能地画出一个面积最小的图形。

生1：我找到了面积最小的图形，不过，我不是画出来的，而是算出来的。

生2：当多边形内部钉子数越来越多，边上的钉子数也越来越多，这多边形的面积就越来越大！

师：反过来，要使面积小，这内部钉子数最少为0，边上钉子数最少为3，还能再少吗？2 行不？算算看。

看似简单的游戏，导入是利用“极限思维”发现规律，提出猜想，在生生“思辨”中发现问题所在，于是，越辨越清晰，由表及里。教师抛出一个有价值的问题，引发生生思辨。教师不动声色，让生生之间进行认知碰撞，迸发思维的火花；答案不完整或错误时，不贸然否定学生的见解，而是给学生充分的时间与空间，让学生展示自己的思维过程。延迟性评价给思维稍慢的学生一个独立思考的时间。最后，教师巧妙地留下“核心问题”，将该矛盾升华。

四、巧设“变式”，“思”“辨”合一

“变式”是对新知本质的深刻理解和内化建构，指教师在分析学生现有知识经验的基础上，充分给予学生时间，通过引导使学生对知识的理解更进一步，对问题的思考更加深刻。或许时间能给他们思想“发酵”的机会，他们的收获会更有价值。

在执教“简单的周期”一课时，笔者在课堂最后的五分钟做了这样的设计：

【祖玛游戏】

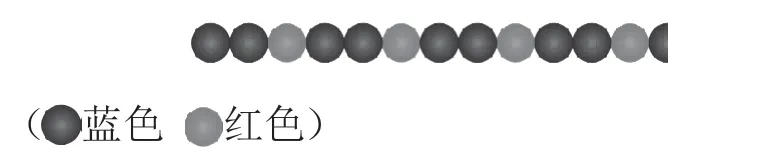
1.玩之前，祖玛的排列有规律吗？这也是一种周期现象。

2.照这样排下去，左起第22 个什么颜色？

3.消失两个蓝祖玛后，左起第22 个什么颜色？

（学生意见不一，教师提醒）

4.（打掉开头两颗蓝色球后）刚才是3 个球为一组，现在还是3 个球为一组，刚才是求第22 个，现在还是求第22 个，为什么两次球的颜色不一样呢？

5.第一次每组是2 蓝1 红，现在是每组1 红2 蓝，什么变了？什么没变？（每组个数一样，但是组内的顺序不一样，也就是规律发生了变化）

6.红色打不掉了（开头反而多了一颗红球），请问，左起第25 个是什么颜色？

7.那减2 呢？减3 呢？减4 呢？

8.哪种方法最简洁？

遵循已知，拓展未知，推陈出新，巧用“变式”。同时，独辟蹊径，让获得的活动经验有得以用武之处。由此，这样的活动经验不再仅仅停留于手指尖、口头上，而是深化于心的思维活动过程，学生在思考中获得的活动经验。

问渠那得清如许，为有源头活水来。缺乏“思辨”的课堂，是沉寂的内河，毫无生机与活力。“百家争鸣”的思维激变，是越说越清晰。教师所说的一定是必要的，无效的一定不说！这压缩的不是时间，留给学生的不是压力，而是更多自主思考的空间、时间、自由、话语权。到达思维终点的路径有很多，但有些学生需要思维的“缓冲”时间与区域，这些都需要教师提供台阶，每个学生都是自己成长站台的守望者，他们前行的速度不一，教师要善做“时差”的调节者，让学生都有“思辨”的机会，越“辨”越清晰、越“辨”越精彩！