应用“认知修订”模型，让审辨思维向高阶漫溯

万川

小学中段是学生自信心形成的關键时期。在“平行四边形的认识”一课中，由于学生首次尝试通过定义的方式来理解概念，他们在如何用数学语言进行完整且规范的表达方面容易遇到困难，对于平行四边形涉及的概念本质也存在一定的理解障碍。为了帮助学生顺利跨越这一难关，培养他们的数学素养和自信心，教师在教学中可以引入“认知修订”的对话模型，帮助学生把握概念的本质，发展审辨思维，养成勇于质疑、慎重思考的思维习惯，为他们在后续学习中批判性思维能力和数学素养的提升打下坚实的基础。

“认知修订”对话模型的应用

在低学段，学生已对某些知识有所涉猎，具备了一定的基础认知，进入中高学段后，针对这些知识点进行深入研究，这样的过程被称为“认知修订”的对话模型。在这一过程中，学生的既有经验和知识得以与新知识形成有效的双向互动，进而促进其认知结构的优化和完善。

根据课型及学生特点，“平行四边形的认识”一课便可运用“认知修订”的对话模型来更好地引导学生学习。从学段和学情角度来看，本课是学生对平面图形的第二阶段的学习，在之前的课程中，学生已经掌握了一些平面图形的基本研究方法及素养。这节课的学习一方面是让学生进一步把握线段、射线、直线的特征，理解构成图形的基本要素的本质；另一方面是让学生为认识其他图形积累一些基本的操作和思维活动经验，为后续图形的测量以及运用图形知识分析解决问题打下基础。

作为一节数学概念课，“平行四边形的认识”的学习目标为：体验平行四边形边的基本特征的数学论证过程，经历实物、几何图形、语言等多种进阶式数学表征的抽象进程；认识平行四边形的高和底，发展抽象能力、空间观念、论证意识、整体思维和推理能力。因此，教师应紧紧围绕“什么样的图形是平行四边形”“什么是平行四边形的高和底”这两个核心问题，组织学生进行系统的探究学习活动，采用“课前预学，激活认知—课上活动探究，修订理解—课后作业补充，拓展思维”的整体思路进行教学设计。

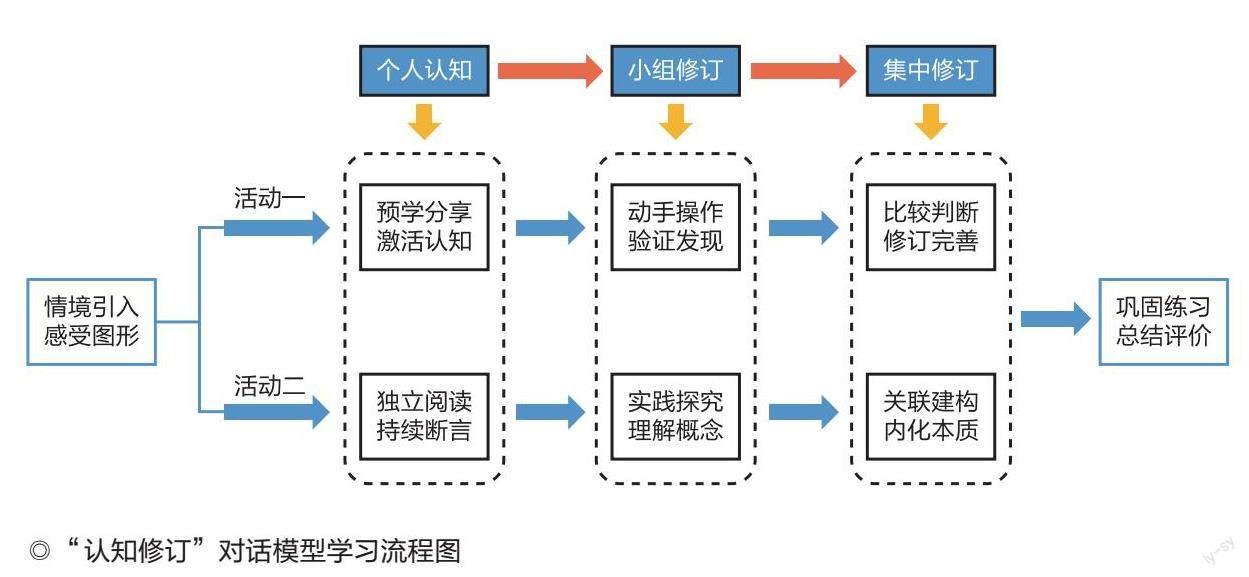
具体来讲，核心活动一为“操作比较，完善认知”。通过三个环节——预学分享、激活认知，动手操作、验证发现，比较判断、修订完善，聚焦“什么样的图形是平行四边形”的问题。核心活动二为“持续探究，理解本质”。通过三个环节——独立阅读、持续断言，实践探究、理解概念，关联建构、内化本质，聚焦“什么是平行四边形的高和底”的问题。在活动过程中，教师应积极搭建合作平台，让学生能够相互倾听和理解，尊重彼此对“平行四边形边的特点”这一论据的发现与论证，交流彼此对“平行四边形的概念”“平行四边形的高和底”的断言，并在两轮的个人认知、小组修订和集中修订中，达成对平行四边形本质特征认识的进阶修订。

对比前测，把握“审辨”思维的逻辑起点

为引导学生思中学，教师可以先通过预学单的方式，把握学生审辨思维的逻辑起点。在讲授“平行四边形的认识”一课前，笔者在两个班级进行了预学单前测，设置了“判断哪些图形是平行四边形”“用一句话描述什么样的图形是平行四边形”以及“关于平行四边形你还知道些什么？还想学些什么”三个问题。通过对预学单的梳理可以得出，学生对平行四边形有一定的认知，但对于平行四边形的描述和分析仍存在困难。预学单前测是促进学生自我思考、真实表达的重要手段。通过预学单前测，学生可以与自己的已有经验进行独立对话，从而深入了解事物的本质。这不仅有助于培养学生的探索意识，还能渗透求真意识，提升其学习效果。同时，预学单前测所获得的数据可以为教师提供明确的参考，帮助教师了解学生的认知起点，为后续学习活动的设计与实施提供方向。

活动论证，发展“审辨”思维的关键能力

以预学单中“描述什么样的图形是平行四边形”的问题为切入点，笔者设计了“动手操作、验证发现”的小组修订环节，让学生通过观察和操作，从具体的实例中归纳出平行四边形边的特点，并进行推理和验证。这种全方位的验证方式不仅丰富了学生对于平行四边形边的认识，也为他们修订原有认知积累了新的补充论据，实现了认知的第一次进阶。在随后的“比较判断、修订完善”的集中修订环节，笔者引导学生结合新的证据，对原有的认知进行分层次的修订。在集体交流和辨析的过程中，通过深入感知、溯因推理和演绎论证，学生们逐渐明确了什么样的图形是平行四边形，进而对平行四边形的概念产生了更加清晰的认识，并深刻体会到“平行”这一核心属性的重要性。这一过程不仅增进了学生对“个人感性认知非终结性断言”的理解，更使他们对定义的合理性有了更加坚定的认知，实现了认知的再次飞跃。

在动手操作、比较验证、修订完善的过程中，以推理论证为载体，学生可以初步体会在数学概念教学中被广泛应用的定义方法的作用，进一步认识到数学知识的关联性和特殊性，建立各个概念之间的联系，提高用数学语言描述现实世界的能力，增强思维的灵活性和缜密性。同时，在抽象概括和合作交流中，学生也提升了探究实践和表达能力，增强了思维的批判性和包容性。

关联建构，培育“审辨”思维的内在核心

在讲解“什么是平行四边形的高和底”时，笔者首先通过“独立阅读、持续断言”环节，引导学生读一读、讲一讲、判一判，形成对平行四边形高和底的初步认知，把握垂线、对边等关键要素。由于这一环节主要停留在视觉辨认层面，缺乏直观的操作体验，因此，接下来笔者又设计了“实践探究”环节，让学生在直观操作中进行对比辨析，突破原有的视觉思维定式。在此环节中，笔者提出了一系列问题，如“高是什么”“底是什么”“同一个平行四边形有不同的高和底是为什么”等，引导学生实现对平行四边形高和底的认知进阶。通过这样的关联建构，学生得以进一步厘清数学知识内部的关系，修正最初对平行四边形认识的断言，深化对平行四边形边的相对性的理解。在辩证想象平行四边形高和底的关系的过程中，学生的几何思维水平从“描述分析”向“抽象关联”发展，实践能力、归纳能力、空间观念、建构思维和辩证意识得到锻炼，实现了审辨思维的高阶发展。

为引导学生进一步思考和探索平行四边形的本质，在最终的巩固练习环节，笔者设计了三个不同层次的问题，即让学生思考“为何某个图形是平行四边形”“为何不同的图形可以通过改变成为平行四边形”以及“某一图形能否通过补画变成平行四边形”。这三个问题的设置，旨在从不同角度深化学生对平行四边形的认识，锻炼他们的辩证思考能力。通过问题的解决，学生不仅能够在多角度的辩证思考中深化对平行四边形概念的理解，实现对平行四边形认知的意义建构，同时也提升了对其内涵和外延的灵活应用能力。这种持续的探索和修订过程，正是培育学生“审辨”思维的核心所在，促使他们以更加开放和多元的视角来审视问题，避免思维的僵化，让学生在观察中思考，在探索中论证，在思辨中实现认知的升华，不断提升自身的批判性思维素养。