负泊松比内凹六边形蜂窝夹层板的吸声性能

孔维凡, 付涛

( 昆明理工大学 机电工程学院，昆明 650500 )

当今隔/吸声复合材料的快速发展，出现了多种隔/吸声结构，蜂窝夹层板结构作为一种简单高效的隔/吸声结构，因其轻质性、高的比强度和比刚度，常被应用到航空航天、汽车、船舶和高速列车等各类载运设备的蒙皮结构中，以此来提升载运设备的隔/吸声性能。夹芯层的结构有多种形式，例如蜂窝形夹芯、波纹夹芯、点阵夹芯、正交加筋夹芯等[1-6]。采用特定排布方式的夹芯层不仅能够在解决噪声方面取得很好的效果，同时夹层板结构轻质化的特性能减轻结构的质量和制造成本。

微穿孔板是一种典型的共振式吸声结构，是在穿孔板共振器基础上发展而来的新型吸声结构，其特点是孔径微小，从而具有更大的声阻[7-13]。传统的蜂窝结构工艺简单，但吸声频宽和性能较不足。张丰辉等[14]通过在蜂窝腔体内加入波纹结构，同时对面板和波纹结构进行微穿孔设计，实现了低频段的有效吸声降噪。刘志恩等[15]针对传统微穿孔板吸声结构吸声带宽较窄的问题，基于微穿孔板串并联耦合机制，提出了3 种不同结构形式的复合微穿孔板结构来进行改进。Liu 等[16]提出了一种智能微穿孔面板，该板由传统的穿孔板和表面粘合压电陶瓷组成，实现了在低频范围内的良好吸声。Rafique 等[17]提出了一种不同深度J 形空腔的不均匀微穿孔板复合结构，该结构在低频范围内有优秀的吸声性能。Jiang 等[18]提出了一种具有N 型混合芯的微穿孔夹层板结构，分析了该结构在宽频域内有出色的吸声性能。Zhang 等[19]研究了在低频范围内，声音通过多孔芯的双壁圆柱壳和内壳微穿孔结构比相应的非穿孔结构在吸声吸能方面更加优秀。Wang 等[20]提出了一种以面心立方为夹层芯的结构，该结构具有优秀的力学性能和声学性能。胡齐笑等[21]基于体积流连续原理，采用改进型传递矩阵法，推导了多穿孔率复合微穿孔板吸声系数公式，探讨了多穿孔率对吸声性能的影响。王卫辰等[22]针对不规则孔的微穿孔板几何参数无法直接获知，造成吸声性能计算困难的问题，提出一种微穿孔板几何参数估算方法。紧接着根据微穿孔板几何参数对高吸声性能区域的影响，探讨了马氏理论适用极限与微穿孔板几何参数的关系，及微穿孔板受粉尘污染后吸声性能演变规律。

微穿孔板和薄板组成的空腔为夹芯层，夹芯层的合理设计可以使夹层板具有更好的吸声性能。负泊松比结构是一种常见的吸声结构，该结构具有轻质性、工艺简单、力学性能和吸声性能优异[23-25]等优点。Kun 等[26]对比了4 种负泊松比材料的吸能情况，得出了蜂窝六边形结构为最优结构，在这种结构下能够优秀的吸收冲击性能。Liu 等[27]对负泊松比蜂窝芯夹芯板进行屈曲和振动研究，得出了蜂窝芯层泊松比为负的板比正泊松比具有更高的承载能力。Qin 等[25]提出了一种具有负泊松比的新型凹形甲虫形结构的设计，该结构采用变密度拓扑优化方法开发，并调整设计参数从6 个数据集中获得最佳结果，结果表明该结构具有优秀的能量吸收性能。Zhang 等[28]针对折返结构变形过程中应力集中和负泊松比的问题，提出一种余弦形折返结构负泊松比超材料。通过将折返结构单元中的斜梁优化为单余弦、串联余弦和多余弦屈曲梁，设计了不同配置的改进折返结构单元，得出了该结构能够使最大应力降低。虞科炯等[29]提出了一种引入正弦函数曲线的负泊松比蜂窝结构，通过改变振幅、胞壁厚度等微结构几何参数，建立了参数化的正弦曲线负泊松比蜂窝结构模型，得出了该结构能够显著地降低峰值冲击力。在对负泊松比结构的研究中，大多数都是关于负泊松比结构力学性能的研究，有关负泊松比结构吸声性能的研究较少。

在此背景下，为了改善传统蜂窝夹层板结构的吸声特性，本文提出了一种负泊松比内凹六边形蜂窝夹层板结构，该结构上面板为微穿孔板，夹芯层为负泊松比内凹六边形蜂窝，其由19 个具有内延伸管的单元腔体谐振器构成，对该结构进行仿真，并通过实验验证了仿真结果的有效性。同时，研究了胞元参数对蜂窝夹层板结构吸声系数的影响。

1 实验与仿真分析

1.1 腔体谐振器的结构设计

图1 为胞元的结构及空间排布方式。构件包含10 个不同尺寸的内延伸管。各单元有序的对称排布，以标号为10 的单元腔体谐振器为中心，单元1～9 围绕中心对称布置。图2 为多个吸声构件组成的圆柱形负泊松比内凹六边形蜂窝结构图，可知，负泊松比内凹六边形蜂窝结构由19 个具有内延伸管的单元腔体谐振器(Cavity resonator with internal extension tube，CRIETs) 组成，各单元腔体结构有7 个参数影响结构的尺寸。通过实验和仿真对胞元倾角、内延伸管孔隙率、内延伸管管长、腔体壁厚及腔体深度进行了调整和选择，从而得到了优秀的吸声性能。

图1 胞元的结构及空间排布方式Fig.1 Structure of cells and spatial arrangement

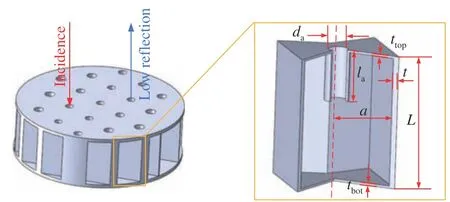
图2 多个吸声构件组成的圆柱形负泊松比内凹六边形蜂窝结构图Fig.2 Cylindrical negative Poisson's ratio concave hexagonal honeycomb structure composed of multiple soundabsorbing components

1.2 实验过程

图3 为B&K 驻波管测量设备及试件照片。如图3(a) 所示，实验设备是B&K 驻波管测量系统(4206，丹麦Bruel&Kjaer Ltd.)，测试范围是500～950 Hz。测量系统由B&K 驻波管、扬声器、放大器、信号处理器、传感器和测试软件组成，测试件是直径为100 mm、高为30 mm 的负泊松比内凹六边形蜂窝结构，放置于B&K 驻波管中间。B&K 驻波管左端的扬声器产生声波信号，位于试件两侧的4 个传感器收集管中的声波信息并反馈至系统，然后由软件计算出结构的吸声系数。如图3(b)所示，通过3D 打印聚乳酸(PLA)材料制作了直径为100 mm、高为30 mm 的圆柱形试样。制备流程如下：首先通过3D 打印出负泊松比内凹六边形蜂窝的壳体，然后打印出圆形面板，最后用胶水将壳体和圆形面板胶粘为一体。试件的各尺寸参数如表1～表3 所示。

表1 胞元的参数Table 1 Parameters of cells

表2 10 个不同尺寸内延伸管的直径daTable 2 Diameter da of 10 different sizes of inner extension pipes

表3 内延伸管的管长laTable 3 Pipe length la of the inner extension pipe

图3 B&K 驻波管测量设备(a)及试件照片(b)Fig.3 B&K standing wave tube measurement equipment (a) and photograph of the specimen (b)

1.3 仿真过程

采用有限元仿真软件COMSOL Multiphysics中的压力声学-频域模块进行仿真。试件模型上方层为空气层，下层为负泊松比内凹六边形蜂窝结构，如图4 和图5 所示，空气域定义为空气，在顶端给予一个端口入射声波1 Pa，通过上层空气层到达下层，仿真模型与实验测量试件的参数相同，试件的边界为硬声场边界，考虑到黏滞效应和热效应对吸声效果的影响，设置了热黏性层阻抗。

图4 负泊松比结构模型的网格划分Fig.4 Meshing of negative Poisson's ratio structure model

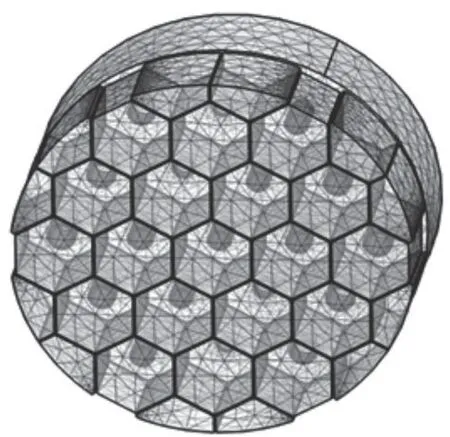
图5 正六边形蜂窝结构模型的网格划分Fig.5 Meshing of regular hexagonal honeycomb structure models

系统整体的吸声系数：

式中：Ei为入射声；Eα为被材料或结构吸收的声能；Er为被材料或结构反射的声能；r为反射系数。

阻抗Z为媒质在波阵面某个面积上的压强与通过这个面积的体积速度的复数比值，其中，体积速度是穿过一面积S的介质流动速度；利用软件中的网格函数，将模型划分为自由四面体网格，预定义为较细化，最小单元大小为1×10-6。对试件模型进行仿真，可以得到结果及模型网格。

1.4 实验与仿真数据对比

图6 为负泊松比内凹六边形结构实验和仿真的频率-吸声系数曲线。可知，实验和仿真结果吻合度较高，通过实验验证了仿真的有效性。在500～750 Hz 之间存在的差异不显著，实验和仿真之间的误差在可接受范围内。在500～950 Hz 内，仿真结果有8 个吸声系数峰值且在700～900 Hz 内有较高的吸声系数。实验与仿真存在误差是由于试件制备时，微穿孔板和蜂窝夹芯结构及底板在胶接过程中，会在底面板上残留少量粘接剂。实验件用胶带缠绕放入B&K 驻波管中，试件和B&K 驻波管管壁之间会存在缝隙，这些因素都对吸声系数的测量存在影响。同时，由于在有限元计算过程中，建立的无壁厚空气域模型忽略了实际情况下较低频段中腔内声波因壁面反射对整体结构耦合效果的影响，因此实测结果会存在有一定的偏差。分别通过实验和有限元仿真得出了负泊松比内凹六边形蜂窝模型在550～950 Hz 之间具有优秀的吸声特性。通过实验与仿真结果的对比，验证了该模型具有优秀的吸声特性。

图6 负泊松比内凹六边形结构实验和仿真的频率-吸声系数曲线Fig.6 Frequency-absorption coefficient curves for experiments and simulations of concave hexagonal structures with negative Poisson's ratio

1.5 负泊松比内凹六边形蜂窝结构与传统蜂窝结构吸声性能对比

图7 为负泊松比内凹六边形蜂窝结构和传统六边形蜂窝结构的频率-吸声系数曲线。可以得出，在相同的结构尺寸下，负泊松比内凹六边形蜂窝结构对于传统蜂窝结构在吸声方面有更强大的性能，在500～550 Hz 之间，负泊松比内凹六边形蜂窝结构的吸声系数大于传统蜂窝结构的吸声系数，在550～600 Hz 之间，负泊松比内凹六边形蜂窝结构的吸声系数略小于传统蜂窝结构的吸声系数，在500～950 Hz 之间，由图4 和图5 经过有限元计算可得，负泊松比内凹六边形蜂窝结构的吸声系数平均值为0.824，传统蜂窝结构的吸声系数平均值为0.78，在研究频率范围内的平均吸声系数提升了5.64%。该结构实质上是以牺牲810～820 Hz、860～890 Hz、920～950 Hz 频率下的性能来换取较低频率下的性能提升和整体频带的平衡。

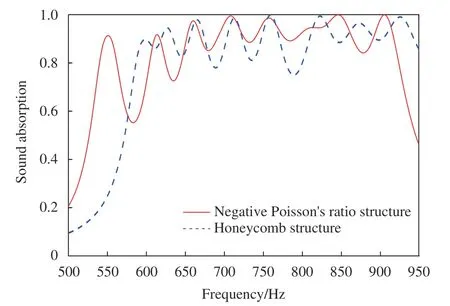
图7 负泊松比内凹六边形蜂窝结构和传统六边形蜂窝结构的频率-吸声系数曲线Fig.7 Frequency-absorption coefficient curves of negative Poisson's ratio concave hexagonal honeycomb structure and traditional hexagonal honeycomb structure

2 结果与讨论

2.1 内凹倾角θ 对吸声性能的影响

圆柱形吸声结构由19 个负泊松比内凹六边形组成，内凹角度θ与结构力学性能密切相关，同时也影响着结构的声学性能，内凹倾角影响着空气腔的体积，由仿真结果可以得出内凹角度对吸声性能存在一定的影响。分别对θ=65°、67°、70°的负泊松比内凹六边形蜂窝结构进行仿真，如图8 所示，随着θ的增大，500～620 Hz 处的吸声系数也有增加，同时，在600～900 Hz 之间，θ=70°时的波谷高于另外两条曲线且平均值大于0.9。随着倾角的增大，空气腔的体积增大，共振频率减小，使其在较低频范围内能够有效的吸声。

图8 不同内凹倾角θ 的负泊松比内凹六边形结构频率-吸声系数曲线Fig.8 Frequency-absorption coefficient curves of negative Poisson's ratio concave hexagonal structures with different concave inclination angles θ

同时，阻抗比变化幅度也验证了内凹倾角θ对吸声性能的影响。如图9 所示，纵坐标为阻抗比Z/Z0，其中，Z0为空气声阻抗，Z0=ρ0c0，空气密度ρ0=1.29 kg/m3，空气中的声速c0=343 m/s。声阻抗的实部常称“声阻”，其虚部称为“声抗”。实部代表着损耗项，反映了声源能量的损耗，能量以声波的形式传播出去了，而虚部代表着能量的贮存。阻抗是机械波传导时介质位移需要克服的阻力，阻抗越大则推动介质所需要的力就越大，阻抗越小则所需力就越小。内凹倾角θ=70°的情况下，具有更平坦的阻抗特性。当结构声阻抗比的实部接近0 时，结构的最大吸声系数随着实部的变大而缓慢减小，随着实部的减小而缓慢增大，结构在此时的吸声系数变化率较小；由图9 声阻比的虚部和图8 中频率-吸声系数的关系可知，负泊松比内凹六边形蜂窝结构在600 Hz、650 Hz、700 Hz、750 Hz、800 Hz、850 Hz、900 Hz频率范围附近的结构声阻抗率的虚部都接近-1，这使结构在此频率范围内的吸声系数均接近结构的极大吸声系数。

图9 不同内凹倾角的负泊松比内凹六边形结构频率-阻抗曲线Fig.9 Frequency-impedance curves of negative Poisson's ratio concave hexagonal structures with different concave inclination angles

2.2 内延伸管孔隙率P 对吸声性能的影响

通过对管径大小的改变，进而影响孔隙率的变化。管径作为内摩擦力产生的重要构件，其结构参数da是影响吸声器共振和系统阻抗的关键因素。孔隙率是面板上管孔的面积与总截面的面积之比，与单一管孔的截面积和管孔数量相关，不同区域的孔隙率主要影响不同的吸声系数峰值。表2 中管径尺寸依次增加0.2 mm，孔隙率分别为P1=10.0416%、P2=10.8544%、P3=11.6992%，同时，全部管径都为表2 中10 个不同管径的平均值da=5.18 mm 时，孔隙率P4=10.73296%，如图10 所示，从整体上来看，当孔隙率变大时，曲线往高频方向移动。在500～600 Hz 时，幅值逐渐升高，在550 Hz 时，P2的吸声系数最高，P2在680～950 Hz 处吸声系数平均值在0.9 以上。因此，可以得出P2在500～950 Hz 频率范围内有着最为平稳的吸声系数曲线。内延伸管管径全部相同的结构在此频率范围内的吸声性能不理想，吸声系数仅有3 个峰值，且在800～950 Hz 频率范围内的吸声系数小于0.5。对比管径相同的负泊松比内凹六边形蜂窝模型，由10 个不同管径的胞元按照一定的排列顺序组成的结构吸声性能优于全部胞元管径相同结构的吸声性能。

图10 不同孔隙率P 的负泊松比内凹六边形结构频率-吸声系数曲线Fig.10 Frequency-absorption coefficient curves of negative Poisson's ratio concave hexagonal structures with different porosities P

减小管径会使孔隙率减小，共振频率降低，能够在低频范围内更好地吸声。通过合理地选择管径的尺寸，可在一定的范围取得良好的吸声效果。不同的管径影响着不同的峰值。较小的管径可以在一定程度上增大结构的声阻，从而获得较大的吸声系数，但过小的管孔却不易制作而且会增加制造成本，而管径过大会导致吸声性能较差，P1的吸声系数在570～670 Hz 频率段内高于P2，而P2在500～950 Hz 中的大多频率段高于P1，P1试件的制作难度和成本都比P2高，但整体吸声效果P2却更好，P2在整体程度上优于P1。因此应根据实际情况选择合适的管径。

2.3 内延伸管管长la 对吸声性能的影响

随着管长的增加，共振频率减小，使吸声系数曲线往更低频方向移动，能够有效消除在更低频范围内的噪声。如图11 所示，730～950 Hz 段内吸声性能的下降主要是由于在这段频率内管长的增加使内延伸管的体积增大，空腔体积减小，阻抗变大，这些都会对吸声性能产生影响，不同内延伸管管长吸声系数的降低幅度又有所不同，管长越长，吸声系数下降的越快。各胞元内延伸管管长相同时，吸声频率范围缩小到700～820 Hz 之间，相比于负泊松比内凹六边形各胞元有着相同的管长值，不等管长值的负泊松比内凹六边形蜂窝结构有着更高的吸声系数。管长依次增加1 mm，如表4 所示。

表4 负泊松比内凹六边形结构试件各胞元内延伸管管长laTable 4 Length of intracellular extension tube la in negative Poisson's ratio concave hexagonal structure specimen

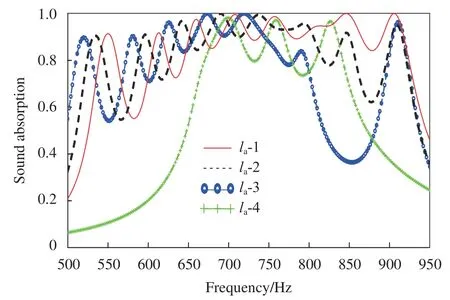
图11 不同内延伸管管长la 的负泊松比内凹六边形结构频率-吸声系数曲线Fig.11 Frequency-absorption coefficient curves of negative Poisson's ratio concave hexagonal structures with different inner extension tube lengths la

采用数值模拟对负泊松比内凹六边形蜂窝结构中的声波能量耗散进行分析，可以得出内延伸管的尺寸在能量耗散方面有着较大的影响。图12给出了两种不同内延伸管管径(从左到右管的直径分别4.7 mm 和4.6 mm)蜂窝胞元结构内的声波能量耗散情况，其中，图12(a)～12(c)分别表示在入射声波频率为550 Hz 时，结构内部的热功耗密度、黏性功耗密度和总热黏性功耗密度。可以看出，与黏性耗散相比，单个蜂窝胞元内的热耗散很小，黏性耗散主要集中在内延伸管处。当声音频率接近共振频率时，内延伸管内的空气柱剧烈振荡，并与管壁之间产生黏性摩擦，从而大幅消耗声波的动能。

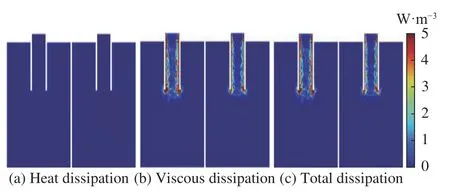
图12 两种不同内延伸管管径的负泊松比内凹六边形结构蜂窝胞元结构内的能量耗散密度云图(从左到右管的直径分别为4.7 mm 和4.6 mm)Fig.12 Energy dissipation density cloud in two different inner extension pipe diameter honeycomb cell cell structures in negative Poisson's ratio concave hexagonal structure ( Tubes diameters from left to right are 4.7 mm and 4.6 mm, respectively)

2.4 腔体壁厚t 对吸声性能的影响

腔体壁厚是影响结构力学性能的重要参数，同时也影响结构的吸声性能。改变腔体的壁厚也会影响结构的振动和声学性能，腔体壁厚对频率-吸声系数的影响如图13 所示，可以看出，在500～600 Hz 和900～950 Hz 之间吸声系数基本没有变化，在700～750 Hz 之间，吸声系数随着壁厚的增加而增加，在650～700 Hz 和750～900 Hz 之间，吸声系数随着壁厚的增加而减小。当腔体壁厚增大时，空腔体积减小，共振频率增大，吸声性能也会相应的减弱，此时，吸声峰值对应的频率向高频移动，在不同频率附近，减小的幅度又有所不同。

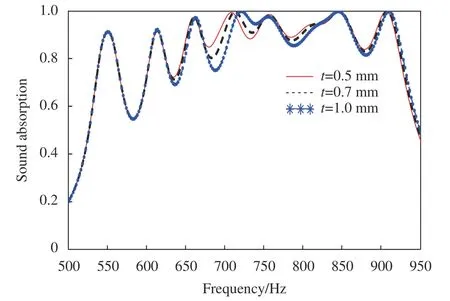
图13 不同腔体壁厚t 的负泊松比内凹六边形结构频率-吸声系数曲线Fig.13 Frequency-absorption coefficient curves of negative Poisson's ratio concave hexagonal structures with different cavity wall thicknesses t

2.5 腔体深度L 对吸声性能的影响

改变负泊松比内凹六边形蜂窝结构的腔体深度对结构的最大吸声系数影响并不大，却对共振频率有着较大的影响。由于该结构是亥姆霍兹谐振器的组合，因此可看作是由质量和弹簧组成的一个共振系统。当入射声波的频率和系统的共振频率一致时，腔体内的空气产生激烈振动摩擦，加强了吸收效应，形成了吸收峰，使声能显著衰减。由图14 可以看出腔体深度越大，共振频率越低，负泊松比内凹六边形蜂窝结构的吸声峰就越往更低频方向移动，因此可以通过较大的腔体深度消除穿透性比较强的低频噪声。但腔体深度的增加又会带来结构体积的增加，试件L=30 mm 在500～950 Hz 中已有较好的吸声系数，同时阻抗的变化率小，对吸声性能的测量不会产生过大的干扰，因此腔体深度的尺寸选择仍需结合实际情况。

图14 不同腔体深度L 的负泊松比内凹六边形结构频率-吸声系数曲线Fig.14 Frequency-absorption coefficient curves of negative Poisson's ratio concave hexagonal structures with different cavity depths L

3 结 论

(1) 通过COMSOL Multiphysics 仿真软件对蜂窝夹层板结构在目标频率范围内进行吸声系数的计算，并运用B&K 驻波管测量系统进行验证，得出了蜂窝夹层板结构在500～950 Hz 低频范围内吸声系数的实验结果基本符合有限元计算的结果。

(2) 负泊松比内凹六边形蜂窝夹层板结构相较于传统的蜂窝夹层板结构有着更优异的吸声性能。夹芯层为负泊松比内凹六边形胞元结构能够有效地减小共振频率，使在更低频的范围内有着优秀的吸声性能。在500～950 Hz 频率范围内，负泊松比内凹六边形蜂窝结构比传统蜂窝夹层板结构的平均吸声系数提升了5.64%。达到了低频高效降噪的目的。

(3) 采用COMSOL 仿真软件研究了胞元参数对蜂窝夹层板结构吸声系数的影响，当胞元倾角增大、内延伸管孔隙率减小、腔体壁厚减小时，结构的吸声性能增强。腔体深度的增加和内延伸管管长的增加都会导致共振频率向更低频方向移动，其中腔体深度的改变更明显。这种内部多腔体结构使其在吸声方面具有巨大的潜力和出色的可设计性。针对不同的应用需求，可以通过合理设计和优化，取得良好的吸声性能。