基于多尺度损伤机制的CFRP 铝合金粘接板冲击行为研究

姚潞, 何文涛, 马岩, 于航, 王艳超, 许家婧*

( 1.南通大学 交通与土木工程学院，南通 226019；2.中国海洋大学 工程学院，青岛 266100；3.南通大学纺织服装学院，南通 226019 )

随着国家“碳达峰、碳中和”目标的提出，如何减少环境污染并提高能源利用率已经成为我国乃至全世界工业领域亟待解决的问题。尤其在交通运输领域，日益增长的汽车排放尾气时刻考验着自然环境，而汽车的质量与油耗、碳排放成正比关系。同时对于电动汽车而言，电池续航里程的大小与车身结构质量是密切相关的，减轻结构质量能显著提高电车的续航里程。因此，汽车轻量化研究对节能减排具有重要意义，是交通结构领域的重要研究方向。碳纤维增强聚合物(CFRP)铝合金粘接板近年来凭借其质量轻、高强度/模量及较优的抗冲击性能等诸多优点，在汽车、航天航空、轨道交通及船舶海工等交通运输领域开始逐渐推广[1-3]。

众所周知，CFRP 与金属板有多种连接方式。对于机械连接(螺栓、铆接等)给结构带来的开孔应力集中与局部缺陷问题，CFRP 与铝合金粘接能够保证结构的完整性，有利于载荷作用内部应力的传递，近年来受到国内外广大学者的关注与研究。针对CFRP 铝合金粘接板，已有学者对其开展了拉伸、弯曲、疲劳等力学特性的研究[4-6]，总结了力学响应的变化规律，揭示了结构的失效模式与损伤演化行为。对于交通结构，不管是汽车碰撞，还是航空器起飞着陆，大部分时候处于较低的速度。另外低速冲击会导致金属塑性变形与结构复杂损伤，为了更好地了解材料的损伤机制，科研人员采用实验方法对CFRP 铝合金粘接板的抗低速冲击行为进行了深入研究。基于复杂的结构组成与不同载荷工况，研究了不同因素对CFRP 铝合金粘接板冲击响应、损伤模式与失效机制的影响[7]。通过不同的加载方式，CFRP 铝合金粘接板内部的损伤特征可以描述为纤维/基体损伤、复合材料层间与金属/复合材料界面之间的分层损伤、金属塑性变形和裂纹，甚至是粘接板内部的穿透和穿孔[8]。实验结果真实可靠，但是花费成本较高，研究周期较长，并且难以深入揭示内部复合材料在载荷作用下的渐进损伤演化过程与失效机制。为了克服实验的缺点，采用数值模拟的方法研究结构在加载过程中的损伤变形与失效模式逐渐受到研究人员的青睐。

近年来随着仿真模拟的推广，根据已有的复合材料数值研究成果，目前常用的有限元模型包括微观力学模型、宏观力学模型及多尺度力学模型。微观力学模型是基于纤维、基体尺度，分析复合材料结构各项组分材料之间的微观断裂损伤行为[9]，但是作为结构而言，微观尺度建模工程巨大，同时耗费大量计算资源，在实际复合材料结构计算过程中难以实现。目前采用最广泛的模型是宏观力学模型，将复合材料简化为各向异性的均质化材料，从而基于宏观力学角度对复合材料结构进行有限元分析。然而宏观模型仅仅分析了结构的宏观力学性能，忽略了纤维/基体内部微观应力对结构宏观应力的影响。其次复合材料的渐进损伤都是基于微观失效开始的，而其宏观模型并不能从微观角度考虑损伤初始。根据实验观察，载荷作用下复合材料都是从微观尺度的损伤失效逐渐开始累积，到一定程度变成宏观可见的损伤模式，这也说明复合材料的宏-微观尺度之间存在必定的某种耦合关系。针对上述问题，一些学者采用多尺度方法建立有限元模型，通过耦合不同尺度模型之间的应力/应变信息来揭示复合材料相关结构的微观损伤失效与宏观力学性能之间的关系。Qi 等[10]通过建立代表性体积单元(RVE)模型施加不同方向的载荷预测了单向CFRP 层合板的宏观力学性能。随后建立简化的细观RVE 模型模拟不同方向铺层的CFRP 层合板结构，并对比实验数据验证了细观模型的准确性。Ge 等[11]采用多尺度分析方法研究了孔隙缺陷对三维五向编织复合材料弹性常数的影响，并通过实验验证了数值模型预测结果的可靠性。Gholami 等[12]创建了一种多尺度平行有限元算法，研究了湿热老化(湿度、温度、时间)对复合材料力学强度的影响。然而上述研究都是通过复合材料的宏-微观信息传递，从而预测其基本宏观力学参数，并没有涉及复合材料结构的损伤失效分析。然而实际的复合材料结构在承受载荷的过程中，往往是从微观尺寸发生损伤失效，逐渐传递到宏观尺寸。因此在宏-微观信息传递过程中，除了常用的模量、强度参数，还需要将材料的宏-微观损伤失效关联起来。王猛等[13-14]通过聚类分析方法，获得用于细观单胞模型向微观单胞模型再向宏观模型传递信息的应力-应变放大因子，完成宏观模型到微观单胞模型的损伤信息传递，并对微观尺度下的模型进行损伤评估与分析，最后通过实验测试对提出模型的准确性进行了验证。蒋宏勇[15]通过桥联模型建立了CFRP 宏细微观损伤模型，结合多尺度损伤耦合分析方法研究了CFRP 薄壁结构的微观损伤模式与宏观力学响应。Ha 等[16]提出了一种微观失效准则(MMF)，并引入应力放大系数(SAFs)将复合材料宏-微观信息进行传递，从而准确预测结构的损伤失效。可以看出，针对纯复合材料的损伤失效，已经有不少科研人员进行了相关的研究并取得了不错的研究成果[17-18]，但是目前关于复合材料金属粘接结构，还都是宏观力学性能分析，很少基于纤维/基体的微观尺度结构分析。

本文针对CFRP 金属粘接板结构，基于应力放大系数考虑宏-微观的应力-应变信息传递，结合MMF 失效准则从纤维/基体尺度计及材料的失效与渐进损伤演化，建立复合材料金属粘接板的有限元数值模型，对其抗低速冲击性能开展研究。首先依据纤维分布，建立微观RVE 模型计算单向CFRP 板的宏观力学弹性参数，并获取应力放大系数矩阵以便后续宏-微观信息传递。随后，借助Fortran 语言开发复合材料宏-微观信息传递的渐进损伤子程序，用于有限元仿真模拟，并基于实验结果对模型的准确性进行验证。最后从纤维/基体微观尺度、粘接面细观尺度及结构宏观尺度出发，考虑纤维体积分布、纤维铺层角度等设计变量对结构的抗冲击性能进行综合评估。

1 CFRP 铝合金粘接板的制备与低速冲击测试

采用热压成型技术制备CFRP 铝合金粘接板(铝板/粘接面/CFRP 板/粘接面/铝板)，铝板采用厚度为0.5 mm 的凯撒2024-T3 板，CFRP 板([0°/90°/0°/90°])为T300 单向碳纤维预浸料(预浸料厚度0.125 mm)按一定方向铺设粘接而成，CFRP 与铝板之间采用环氧树脂加热粘接(厚度忽略)，最终一体化成型CFRP 铝合金粘接板。为了实验方便，将成品用数控机床切割成实验件大小，长150 mm、宽40 mm、厚度1.5 mm。

低速冲击试验采用的设备为Instron 9400 落锤冲击试验机[19]，如图1 所示，整个设备包括冲头、夹具、传感器、反弹射装置等。在落锤冲击实验中，冲头的冲击速度是通过调节冲头高度来实现的。本文用到的冲头质量为5.23 kg，在冲头接触到试件发生反弹时，冲击试验机中安装的气动卡具将会卡住弹起的冲头，以免冲头的二次冲击对实验装置造成不必要破坏。

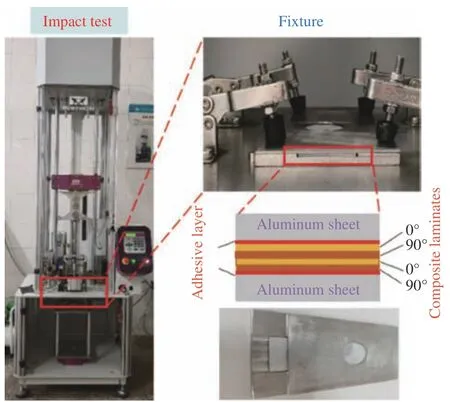
图1 碳纤维增强聚合物(CFRP)铝合金粘接板的低速冲击实验Fig.1 Low-velocity impact test for carbon fiber reinforced polymers(CFRP) aluminum alloy adhesive plate

2 RVE 模型的构建与验证

本文首先考虑纤维体积分数，建立微观纤维/基体的RVE 模型，对RVE 模型施加周期性边界条件与单位载荷，最后根据均质化理论计算单向CFRP 预浸料的力学弹性参数，并通过实验数据验证RVE 模型的准确性。

2.1 RVE 模型的周期性边界条件

为了解决RVE 模型的边界位移与边界应力不连续问题及相邻RVE 单元的相互作用，有必要采用周期性边界条件准确模拟微观结构的力学行为[20]。对于周期性边界条件，理论上要求在RVE模型中相对面必须具有一样的节点坐标，并且建立相应的约束方程来绑定每对节点，构成互相影响的关系，如图2 所示。本部分将相对面节点的位移插值设为常数，公式如下所示：

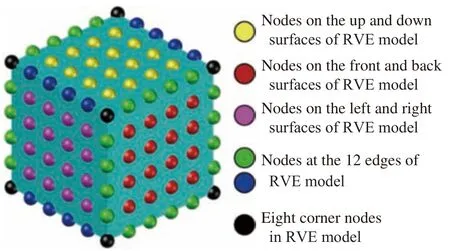
图2 代表性体积单元(RVE)模型的单元节点分布规律Fig.2 Distribution rule of nodes in representative volume element(RVE) model

2.2 不同RVE 模型的构建与对比

关于RVE 模型的选择也有很多种，包括正方体、六面体模型，还有纤维随机分布的RVE 模型。本文建立了5 种不同的RVE 模型(图3)，所有的模型中纤维的体积占比都是60vol%，正方形、均匀分布(25 根纤维)、随机分布1 (纤维直径0.2)、随机分布2 (纤维直径0.1)，4 种情况的边长都是1；长方形的短边为1，长边为，纤维与基体的材料属性如表1 所示[16]。分别对这5 种RVE 模型施加周期性边界条件，最终计算出对应的单向CFRP 力学性能参数，如表2 所示。为了更清楚地观察不同RVE 模型预测结果的准确性，将预测结果与实验结果(单向CFRP 预浸料产家提供)对比分析，如图4 所示。从图中看出，因为均匀分布的RVE 模型可以看成正方形的排列组合，所以这两种情况预测结果十分相近。随机分布1 因为纤维直径较大，纤维之间的基体分布多，对其力学弹性参数的影响较大，所以误差最大。长方形与随机分布2 的RVE 模型预测结果相对较好，但是随机分布2 的模型内部纤维数量较多，在划分网格计算分析时会占用较多的计算能耗，因此本文最终选择长方形的RVE 模型对复合材料的力学性能进行预测，同时也为计算宏-微观模型之间应力放大系数奠定基础。

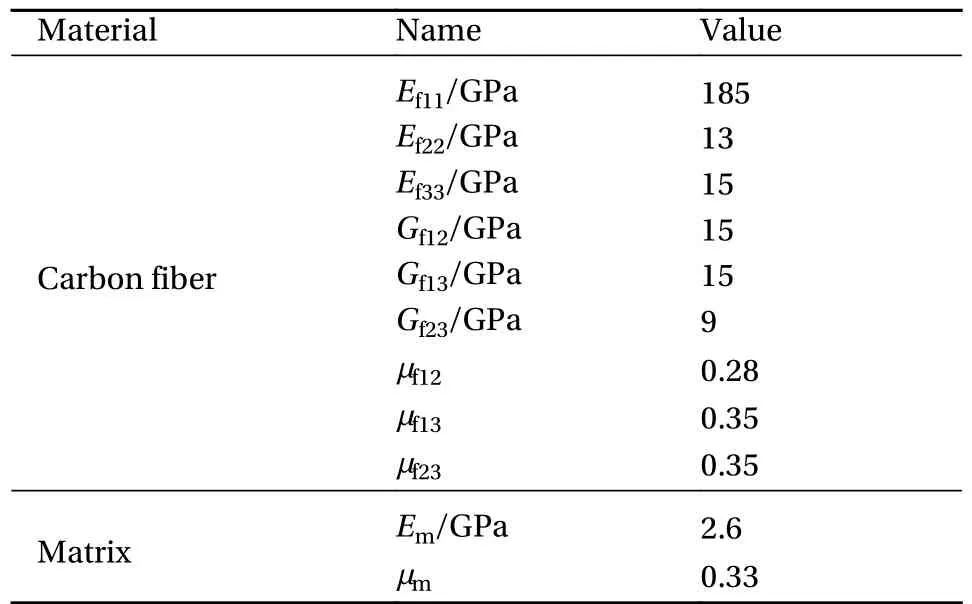
表1 T300 碳纤维与基体的力学性能参数Table 1 Material properties of T300 carbon fiber and matrix

表2 CFRP RVE 模型力学性能参数与实验对比Table 2 Comparison of RVE models of CFRP and experimental tests

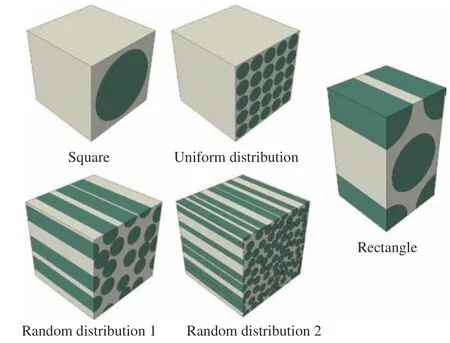
图3 不同的CFRP 的RVE 模型Fig.3 Different RVE models of CFRP

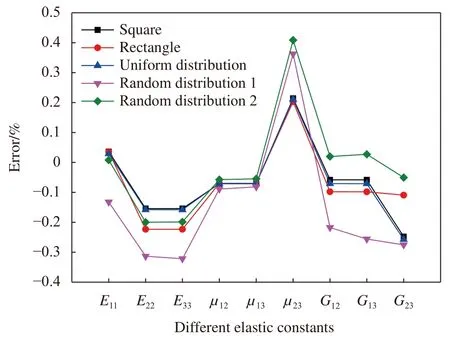
图4 不同CFRP RVE 模型弹性常数的数值与实验误差Fig.4 Numerical and experimental error of elastic constants for different CFRP RVE models

2.3 宏-微观应力放大系数

为了在后期宏观结构分析过程中考虑纤维/基体的微观损伤失效及演化过程，需要确定结构在计算过程中宏-微观应力转化放大系数，进而从宏观应力计算得出微观应力[21-22]。这里先建立单向CFRP 的长方形六面体RVE 模型，施加周期性边界条件，并对RVE 模型施加宏观单位荷载工况。为了计算纤维与基体的微观应力，在RVE 模型中的纤维基体部分选择一些有代表性的参考点，且尽可能的扩大选点范围，如图5(a)所示。图中F代表纤维，选取了8 个点，M 代表基体，选取了10 个点，下标分别表示取点顺序。随后对RVE 模型施加宏观单位载荷并开始计算，如图5(b)所示，最后通过提取参考点的应力计算每个参考点的应力放大系数Mi，公式如下：

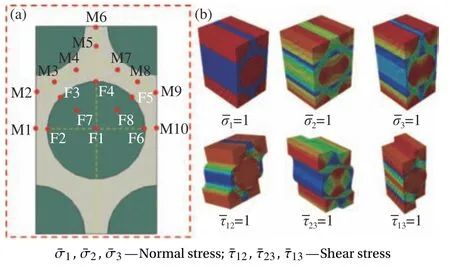
图5 CFRP RVE 模型的选点分布(a)及宏观单位载荷加载工况(b)Fig.5 Distribution of key points (a) and macro unit loadings (b)in RVE model of CFRP

3 CFRP 铝合金粘接板数值模型的建立

在对CFRP 铝合金粘接板进行数值模拟的时候，必然会考虑不同材料的本构模型，本章节分别介绍CFRP 基于微观应力的失效准则、损伤演化模型，铝合金的延性损伤模型及粘接面的内聚力损伤失效模型。

3.1 CFRP 微观失效准则与渐进损伤演化模型

3.1.1 复合材料微观失效准则

在对结构进行宏观加载分析时，采用上述应力放大矩阵将宏观应力转换成微观应力，基于MMF 微观失效准则[23-24]对复合材料的微观损伤模式进行判断。

(1) 纤维失效准则(最大纵向应力准则)：

其中：σ1为微观尺度下纤维参考点在1 方向的微观应力；T 与C 分别代表拉伸与压缩状态；分别表示纤维在拉伸与压缩状态下的失效强度。

(2) 基体失效准则(改进的Von Mises 准则)：

其中：σ1、σ2、σ3、σ12、σ23、σ13为RVE 模型中对应的基体参考点的应力分量；分别代表了基体的拉伸强度和压缩强度；l1表示基体的第一应力不变量；是参考点的临界Von Mises应力；是临界第一应力不变量。

3.1.2 微观损伤演化模型

(1) 纤维损伤演化模型：

当纤维积分点应力满足失效条件时，其损伤演化规律如下所示：

式中：σf表示纤维微观尺度应力；为纤维拉伸、缩的损伤变量，在计算过程中取所有参考点的最大值。

当纤维发生损伤后，其弹性参数可以按照下式进行折减：

式中：Ef1、Ef2分别是纤维未发生损伤时沿纤维方向和垂直于纤维方向的弹性模量；是损伤发生后沿纤维方向和垂直于纤维方向的弹性模量。

(2) 基体损伤演化模型：

基体采用等效应力描述损伤演化过程，具体如下式所示：

其中：km是基体损伤后的最大等效应力；γ代表基体的损伤形状参数；为基体的损伤因子，由基体的应力状态计算可得。

材料发生损伤后，与纤维一样，基体的力学性能也会出现下降，按照下式进行衰减：

式中：σm代表基体的微观应力；Cm代表基体的初始刚度矩阵；Em、分别表示基体材料在损伤前后的弹性模量；εm代表基体的微观应变；表示基体的损伤变量，取所有参考点的最大值。

3.1.3 宏观损伤演化模型

上述材料损伤演化是基于纤维/基体微观尺度，然而在结构计算时都是宏观应力应变，因此在计算得到微观损伤演化规律后，需要将微观损伤变量转换成宏观损伤变量，从而继续到宏观结构里面进行迭代计算：

式中：E1、E2代表宏观单向碳纤维预浸料在1 和2 方向的弹性模量；Vf、Vm分别表示预浸料内碳纤维与基体的体积分数；d1、d2表示单向预浸料在1、2 两个方向的宏观损伤变量，最终损伤后的宏观结构刚度矩阵更新状态如下：

式中：Cij代表损伤后的宏观刚度矩阵；代表初始刚度矩阵。

3.1.4 复合材料多尺度模型框架及有限元计算流程

复合材料结构考虑纤维/基体微观尺度损伤，计算宏观力学性能的步骤可以分为如下几步，如图6 所示流程：

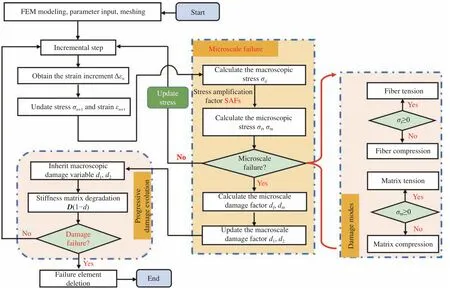
图6 考虑纤维/基体微观损伤的复合材料渐进损伤演化程序Fig.6 Progressive damage progress of composite laminates based on the fiber/matrix micro-damage

(1) 依据纤维基体体积分布，建立合适的RVE模型并选择合适的参考点；

(2) 对RVE 模型施加单位宏观荷载，提取参考点的微观应力，组成应力放大系数矩阵；

(3) 基于应力放大系数矩阵，根据宏观结构有限元计算结果，计算对应积分点的纤维/基体微观应力，再依据微观失效准则，微观损伤演化规则，宏观损伤演化规则，更新材料的宏观刚度矩阵，继而进行有限元中的迭代更新计算，多尺度损伤模型的所有输入参数如表3 所示。

表3 CFRP 多尺度模型的需求参数Table 3 Parameters of CFRP multiscale model

3.2 铝合金延性损伤演化模型

铝合金是一种各向同性材料，本文采用2024-T3型号铝合金，选用ABAQUS 提供的各向同性弹塑性本构模型进行模拟，相关材料参数可以通过实验测得，如表4 所示[25]。该模型采用延性损伤演化理论(Ductile model)来描述材料的损伤起始和损伤演化。对于延性损伤准则，损伤起始条件如下：

表4 2024-T3 铝合金板的材料属性Table 4 Material properties of 2024-T3 aluminum

式中：ωD为一个随着应变单调递增来表征损伤的状态变量；pl为等效塑性应变，用来表征材料的损伤程度，定义域为[0, 1]；η为应力三轴度；为等效塑性应变的应变率；为损伤起始的等效塑性应变。一旦损伤在某个积分点发生，该积分点所在单元被视为失效，随后将被从模型中删除。

3.3 粘接面内聚力损伤模型

金属层/复合材料层之间的分层损伤起始及传播是结构在载荷作用下的重要失效模式。本文采用了ABAQUS 内置的内聚力模型来模拟结构中金属/复合材料之间粘结层的损伤初始与演化。粘结层的初始线弹性行为基于牵引-分离准则，伴随着分层损伤的初始及演化。线弹性行为可以表示为

其中：tn、ts、tt代表不同方向的界面牵引力；εn、εs、εt代表不同方向的应变；Enn、Ess、Ett代表不同方向的刚度系数(两个面内剪切方向，一个厚度方向)。在计算过程中，需要判断内聚力单元是否达到损伤失效，本文采用了二次名义应力准则：

当内聚力单元达到损伤起始后，开始进入刚度衰减过程，本文采用了B-K 损伤演化准则计算断裂能：

表5 内聚力单元参数Table 5 Material properties of cohesive elements

3.4 CFRP 铝合金粘接板有限元模型及验证

本文采用ABAQUS 软件对CFRP 铝合金粘接板有限元模型进行建模，如图7 所示。CFRP 层合板与上下表面铝板采用实体单元C3D8R 进行建模，CFRP 与铝板之间的粘接面采用内聚力单元(Cohesive element)模拟。在CFRP 铝合金粘接板上、下都采用钢板进行固定，钢板与冲头在模型里面都被设置成刚性体。粘结板结构与固定板及冲头之间的接触设置成通用接触，摩擦系数设为0.3。在对结构进行网格划分时，冲击区域的网格局部细化(1 mm)，其余区域的网格划分为2.5 mm。冲击能量通过给冲头一定的初始速度来实现，本文冲头质量为5.277 kg，因此基于能量等效，40 J的冲击能量相当于冲头3.894 m/s 的初速度。

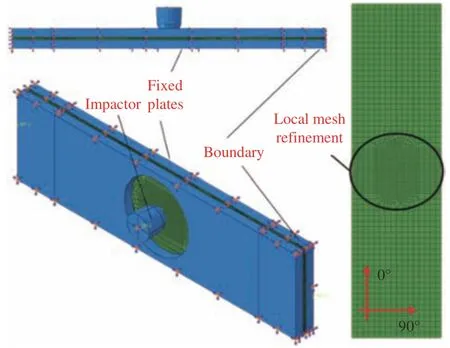
图7 CFRP 铝合金粘接板的有限元模型Fig.7 Finite element model of CFRP aluminum alloy adhesive plate

图8 对比了CFRP 铝合金粘接板在冲击载荷作用下的实验与数值仿真结果。通过载荷-位移曲线对比可知，仿真模型的冲击载荷峰值在5.12 kN，实验测得的冲击载荷峰值为5.40 kN，两者误差为5.18%。除此之外，数值模拟的冲击载荷曲线在上升阶段与初始下降阶段都较准确地预测了载荷的趋势，尤其是在点A、B 处，仿真模型都较准确地预测到了载荷的变化。只有在下降阶段后期，难以保证曲线走势的高度统一。这主要是由于复合材料的失效模式复杂多样，使结构冲击损伤后的力学性能难以准确预测，最终导致冲击载荷下降的后面阶段预测值与实验值出现部分误差。图9 展示了结构在冲击载荷作用后的损伤失效形貌，实验与数值模拟结果都刻画出结构的圆形损伤区域。在40 J 的冲击能量下，粘接板反面也能看到明显的穿孔，表明冲头几乎全部贯穿了CFRP铝合金粘接板。由此可见，本文基于复合材料多尺度损伤机制建立的CFRP 铝合金粘接板数值模型，能够较准确地预测结构的低速冲击载荷-位移响应，捕捉响应的突变时刻及结构的失效形貌。

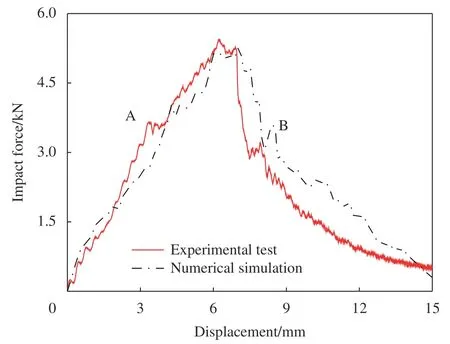
图8 CFRP 铝合金粘接板的数值与实验冲击载荷-位移响应对比Fig.8 Comparison of impact load-displacement curves of experimental and numerical results of CFRP aluminum alloy adhesive plate

图9 冲击载荷后CFRP 铝合金粘接板的失效形貌对比Fig.9 Comparison of damage morphologies of CFRP aluminum alloy adhesive plate after impact

4 结果与讨论

对于上文开发的考虑复合材料多尺度损伤的CFRP 铝合金粘接板冲击加载有限元模型，结合实验结果验证了模型的准确性。本部分基于该模型，数值模拟研究了复合材料中纤维不同铺层方向与不同体积分布对结构抗冲击性能的影响，并对比了它们的冲击载荷响应与失效模式。

4.1 纤维铺层方向对CFRP 铝合金粘接板冲击行为的影响

碳纤维板是由众多单向CFRP 预浸料以一定的角度叠加铺设而成，因此其整体的力学性能与纤维铺设角度密不可分。本部分将纤维层合板内四层单向纤维层分别设置成[0°/90°/0°/90°]、[0°/0°/0°/0°]、[45°/-45°/45°/-45°]、[90°/90°/90°/90°]，基于数值模拟研究分别预测不同结构的冲击响应与失效形貌。

图10 列出了不同纤维铺设角度下CFRP 铝合金粘接板的冲击载荷-位移曲线与冲头冲击过程中的结构吸能曲线。可以明显看出，4 种铺层方式下结构的冲击载荷位移曲线几乎类似，尤其在曲线上升阶段。在载荷曲线达到峰值之后，伴随着不同铺层角度导致的损伤失效不同，后期的冲击载荷逐渐呈现波动式下降。从不断增加的冲头位移可以看出，冲头在冲击过程中一直向下，没有出现回弹，表明最后冲头的冲击动能一部分转换成了CFRP 铝合金粘接板的变形能，另一部分被结构的复杂损伤失效所耗散。由吸能曲线可以看出，4 种不同铺层角度下，结构整体的吸能情况也非常相近，能量先是快速上升，在冲击后面阶段逐渐趋于平缓，最终达到40 J 的能量值。综上所述，不同纤维铺层方向对CFRP 铝合金粘接板的抗冲击力学响应几乎没有影响。

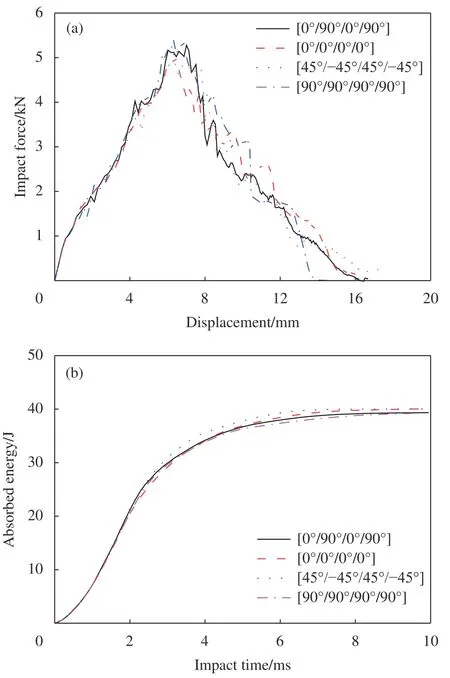
图10 不同铺层方向下CFRP 铝合金粘接板的冲击响应Fig.10 Impact response of CFRP aluminum alloy adhesive plate under different layer angles

图11 列出了不同铺层方向下CFRP 铝合金粘接板冲击后的变形损伤。由于铺层方向只是改变了复合材料层在面内方向的力学性能，对于厚度方向的力学性能影响较小，因此图中不同工况的应力云图并没有显示出较大的区别。

图11 不同铺层角度下CFRP 铝合金粘接板的冲击损伤形貌Fig.11 Damage morphologies of CFRP aluminum alloy adhesive plate under different layer angles

为了更清楚地观察内部复合材料层的失效模式，图12 列出了内部4 层复合材料层的损伤应力云图，图中仅截取了粘接板中间的受冲击部分。在第一种工况([0°/90°/0°/90°]) 中，第一层为0°铺层纤维，第二层为90°铺层纤维，因此在冲头冲击过后，第一层的纤维出现沿着90°方向的断裂，第二层纤维出现沿着0°方向的断裂。第二种工况([0°/0°/0°/0°])与第三种工况([90°/90°/90°/90°])中的复合材料层都为单向铺层，因此整体CFRP 板出现了明显的纤维裂纹，第二种工况中纤维铺层都沿0°方向，因此表示纤维断裂的单元删除沿着90°方向。而第三种工况完全相反，纤维铺层都沿90°方向，表示纤维断裂的单元删除出现在0°方向。在第四种工况([45°/-45°/45°/-45°])中，因为铺层方向沿着±45°方向，所以明显的单元删除也出现在斜向方向。除此之外，图中的应力云图也明显受到纤维铺设方向的影响，应力集中的方向与纤维铺设方向一致。

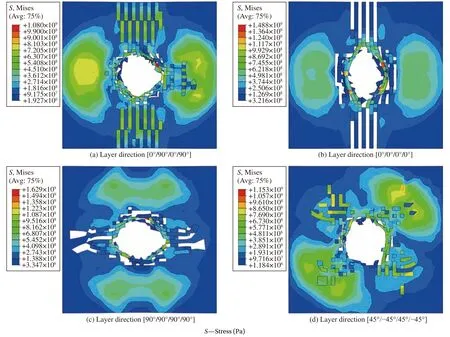
图12 不同铺层角度复合材料层失效模式Fig.12 Failure models of CFRP under different layer angles

4.2 纤维体积分数对CFRP 铝合金粘接板冲击行为的影响

单向CFRP 预浸料的力学性能与其内部的纤维体积分数密不可分。本部分基于纤维/基体的复合材料多尺度模型，对碳纤维体积分数与结构的抗冲击性能的关系进行数值模拟研究。表6 给出了不同纤维体积分数的RVE 模型力学弹性参数，显然单向CFPR 预浸料的拉伸模量与剪切模量都随着纤维体积分数的增加而变大。基于表中的弹性参数，结合第四章节建立的CFRP 铝合金数值模型，研究不同纤维体积分数粘接板的抗冲击性能。图13 展示了不同纤维体积分数Vf情况下冲击载荷-位移曲线与粘接板的吸能曲线。不同于纤维铺层方向的改变，Vf的变化对结构的抗冲击响应有较大影响。从载荷-位移曲线图中，可以看出当Vf=0.4 时，冲击载荷的峰值比其他几种工况都要大；而Vf=0.8 时，冲击载荷峰值相对最小。这可能是由于低Vf时，结构弹性模量较小，从而表现出较低的刚度。由于低Vf的CFRP 铝合金粘接板抵抗变形的能力较差，在冲头接触的一瞬间，冲头表面与粘接板接触面积较大，从而引起较大的冲击载荷峰值。根据冲头的最终位移情况可以看出当Vf较低时，冲头的位移达到一定位置后不再增加；反之Vf较大时，冲头位移一直增加，即使当冲击载荷为0 时，位移还是继续变大。结合图14 的变形形貌可知，在低Vf时，结构变形多为弹性变形，冲头冲破粘接板后多为结构与冲头的摩擦力在阻止冲头继续向下移动；而高Vf时，冲头冲击瞬间结构发生失效损伤，粘接板模型单元在冲击处都被删除，此时冲头在冲破粘接板后继续向下移动。从吸能曲线图也可以看出，由于摩擦力的产生，低Vf的粘接板吸收冲击能较多；而在高Vf的粘接板冲击过程中，结构在被冲破的瞬间出现较多单元删除，后期不在有摩擦力的产生，因此最终整体结构吸收冲击能较小。

表6 CFRP 铝合金粘接板RVE 模型力学性能参数与实验对比Table 6 Comparison of mechanical parameters of RVE model of CFRP aluminum alloy adhesive plate and experimental tests

图13 不同纤维体积分数Vf 的CFRP 铝合金粘接板的冲击响应Fig.13 Impact response of CFRP aluminum alloy adhesive plate under different fiber volume fractions Vf

图14 不同纤维体积分数的CFRP 铝合金粘接板的失效形貌Fig.14 Damage morphologies of CFRP aluminum alloy adhesive plate under different fiber volume fractions

从结构的失效形貌图14 可以看出，当纤维体积含量较低时，应力波传播范围较大，整体结构的弹性变形范围比较广，但是整体结构的穿孔比较小。这是由于当CFRP 铝合金粘接板被冲破后，随着冲头的拔出，粘接板会出现回弹现象，最终影响了结构的穿孔大小。而当纤维体积分数变大后，粘接板的穿孔面积逐渐在变大，表明在被冲头冲破时，粘接板出现了较多的单元损伤删除，从而当冲头拔出后不再会影响穿孔面积。同样的现象从图15 的纤维层损伤图中也可以看出，随着纤维体积分数的增加，纤维层的穿孔面积也逐渐变大。这些结构的损伤失效现象也都验证了之前冲击响应规律的发生。

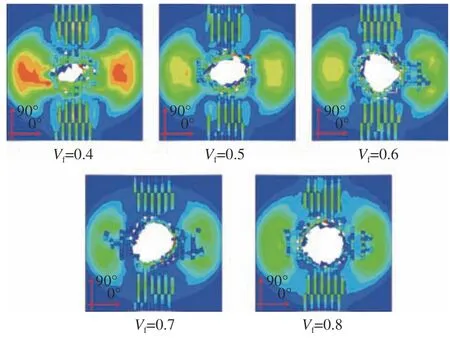
图15 不同纤维体积分数下复合材料层失效模式Fig.15 Failure models of CFRP under different fiber volume fractions

5 结 论

从纤维/基体微观尺度出发，借助应力放大系数考虑复合材料宏-微观的结构信息传递，结合微观失效准则(MMF)从纤维/基体尺度考虑复合材料的初始失效与渐进损伤演化，再考虑碳纤维增强聚合物(CFRP)/铝合金粘接面的损伤本构模型，建立CFRP 铝合金粘接板的多尺度有限元模型，对其抗低速冲击性能开展数值模拟，并参数化研究内部纤维铺层方向与纤维体积分数对结构冲击行为的影响。

基于本文的研究，最终可以总结出一些结论如下：

(1) 基于纤维/基体尺度建立不同的微观代表性体积单元(RVE)模型，在综合考虑计算效率与精度后，选择长方形RVE 模型预测单向CFRP 预浸料的力学弹性参数；

(2) 借助微观RVE 模型计算应力放大系数实现复合材料宏-微观信息传递，结合MMF 失效准则考虑复合材料初始失效与渐进损伤演化的宏-微观转换，并考虑CFRP/铝合金粘接面建立CFRP 铝合金粘接板的数值模型，最终准确预测结构的抗冲击响应与失效模式；

(3) 通过对结构的参数化模拟分析，结果表明CFRP 铺层角度的变化对CFRP 铝合金粘接板的抗冲击性能影响有限，最终的载荷响应与吸能效果都相近，只是由于纤维铺层方向的不同，内部复合材料的失效模式有所变化；

(4) 纤维体积分数对CFRP 铝合金粘接板的抗冲击性能影响较大，体积分数较低时，冲击载荷较大，结构损伤范围较广，以结构弹性变形为主；纤维体积分数较大时，冲击载荷较小，结构损伤范围局限于冲头接触区域，结构单元失效删除较多。