基于能量准则的复合材料层合板低速冲击近场动力学模拟

姜晓伟, 汪海, 朱建辉

( 1.中国航发商用航空发动机有限责任公司，上海 200241；2.上海交通大学 航空航天学院，上海 200240；3.南京航空航天大学 航空学院，南京 210016 )

航空复合材料结构在服役过程中承受的冲击载荷来源广泛，如航空发动机复合材料风扇叶片所受的鸟撞冰撞冲击载荷、复合材料风扇机匣所受的叶片飞脱冲击载荷及飞机复合材料机翼、机身所受的冰雹、鸟撞冲击载荷等。航空复合材料结构冲击相关的验证试验往往成本巨大、实施困难，因而航空工业界对于可靠、稳定的复合材料冲击损伤分析方法具有迫切需求。复合材料低速冲击(Low-velocity impact，LVI) 模拟是航空复合材料结构冲击分析的一个重要问题，复合材料承受LVI 载荷，易在材料内部引发目视不可检分层损伤(Barely visible impact damage，BVID)，这种服役过程中极易出现检测逃逸的损伤会进一步扩展导致结构的整体性破坏。

目前航空复合材料结构冲击损伤所采用的模拟分析手段大多基于有限元方法(FEM)[1-3]，有限元方法在复合材料分析领域发展多年，已经得到了大量的实例验证并应用于型号任务的复合材料结构设计分析工作。但是正如这些研究工作[4-6]中指出的，有限元理论建立于连续介质力学的基础之上，其连续性假设和基于偏微分方程的理论架构，在处理诸如复合材料冲击损伤裂纹扩展等不连续性问题上，始终存在着底层理论上的先天缺陷，造成比如网格无关性差、损伤扩展路径需要预制、控制参数物理意义不明确及三维耦合损伤扩展难以分析等困难。尽管近年来出现了如扩展有限元(XFEM) 等有限元框架下的新理论，有限元方法在复合材料冲击损伤分析领域的困难依然未得到彻底解决。

近年来，Silling 等[7-9]提出的近场动力学理论(Peridynamics，PD)作为计算力学领域的前沿性理论，在复合材料冲击损伤模拟与分析中体现出了一定的优势。Xu 等[4]采用键基近场动力学方法分析了复合材料层合板的冲击损伤，基于键临界伸长率准则给出了低速冲击引发的分层和基体损伤，模拟得到的不同冲击能量下的损伤面积与试验值吻合得很好；Askari 等[10]采用键基近场动力学研究了混杂铺层复合材料高能量和低能量下的冲击问题；Sun等[11]模拟了复合材料层合板在不同冲击速度下的损伤，推导了应变率相关的键基近场动力学本构模型，讨论了冲击速度对损伤模式和损伤面积的影响；Zhou 等[12]研究了复合材料面内动态破坏过程，采用了裂纹速率相关的动态断裂韧性，在此基础上，Zhou 等[13]进一步模拟了三维复合材料层合板的冲击损伤，给出了面内损伤模式和面外分层；Baber等[14]采用键基PD 模拟了z-pin 复合材料低速冲击损伤，定量地比较了模拟与试验的冲击力和分层损伤面积，两者符合得很好；Weckner 等[15]研究了近场动力学模拟复合材料高能量冲击问题(HEDI)，盲测(Blind prediction)的结果表明，近场动力学能够预测高能量冲击过程中复合材料层合板的损伤模式、冲击力及面外位移。Wu 等[16]采用非常规态近场动力学模型模拟了玻纤层合板在低速冲击下的动力学断裂过程，在非常规态框架下考虑了材料的粘弹性效应，仿真的断裂模式与试验结果吻合得很好。Baber 等[17]采用一种改进的近场动力学方法模拟了复合材料低速冲击损伤，考虑了层内和层间的剪切非线性及应变率效应，仿真的结果和试验结果吻合得很好。目前为止，还未见到基于能量准则的复合材料层合板低速冲击近场动力学模拟工作。

本文应用常规态近场动力学理论模拟复合材料层合板低速冲击损伤过程，并引入用于复合材料低速冲击损伤判定的能量准则。在建立的球型域常规态近场动力学复合材料模型基础上[18]，基于考虑时间步长下不同断裂混合比的能量失效判定准则，模拟复合材料低速冲击损伤过程，获取冲击接触力、分层损伤面积及分层形状。首先对复合材料低速冲击近场动力学模拟的模型刚度进行验证，对比近场动力学模拟的冲击接触力、冲击速度及冲击位移与有限元结果的一致性。再开展复合材料低速冲击近场动力学损伤模拟，定量比较近场动力学模拟结果与试验结果的冲击力、分层损伤面积及分层形状，并给出冲击过程中复合材料层合板纤维断裂、基体开裂及分层损伤扩展的过程。文中的数值计算采用GPU 并行计算，选用PGI CUDA FORTRAN 编译器。

1 复合材料近场动力学计算模型

1.1 控制方程

本文所选用的计算模型是球型域常规态复合材料近场动力学模型[18]，该模型是在Madenci等[19]、Colavito 等[20-21]提出的近场动力学层合板理论(PDLT)的基础上建立的，该模型可以考虑横向泊松比效应。模型的控制方程为

图1 近场动力学符号Fig.1 Peridynamic notations

其中，

其中，

其中：s(k)(j)是PD 键的伸缩比；代表的是面内纤维方向或垂直于纤维方向的键伸缩比；δ是域的半径，且

三维的PD 体应变θ(k)定义为

PD 复合材料模型中的材料参数a、d、b、bF、bT的计算公式为

其中，C11、C22、C33和C55是正交各向异性复合材料刚度矩阵C的参数，定义为

其中：ν为泊松比；E为弹性模量；G为剪切模量。

1.2 基于能量的失效判定准则

对于冲击分层损伤，引入了考虑时间步长下不同断裂混合比的能量失效判定准则。在每一个时间分析步，分别计算物质点I 型、II 型及III 型不同断裂模式的累积吸收功，再根据当前分析步的断裂混合比，计算得到物质点的临界层间断裂韧性。基于能量准则的复合材料低速冲击近场动力学损伤判定过程如下所示：

(1) 计算物质点i在当前时间步吸收的功率pIabs(i)、pIIabs(i)、pIIIabs(i)：

其中：H为积分域；v'为键关联物质点速度；v为物质点速度；V'为物质点体积。

(2) 计算物质点i累积吸收的功wI(i)、wII(i)、wIII(i)：

其中，k为第k个时间步。

(3) 计算物质点i层间断裂韧性Gc(i)：

其中，GIc、GIIc为I 型、II 型层间断裂韧性；η为相关系数。

(4) 计算物质点i对应键的临界断裂功wc(i)

键临界断裂功的推导过程见文献[22]：

(5) 计算当前时间步键(i,j)累积吸收的功wt(i,j)：

(6) 判定键(i,j)是否不可逆地断开

如果(wt(i,j))/(wc(i))≥1，则认为该键不可逆地断开。

对于冲击面内损伤，考虑纤维断裂和基体开裂两种损伤模式，判定准则参考Hu 等[23-24]，当两个物质点之间的键伸长率超过一个临界值，就不可逆地断开键的连接。面内纤维方向键和其他方向键的临界伸长率的计算公式为

其中，XT、XC、YT、YC是复合材料的强度值。

损伤状态变量µ定义为

纤维断裂、基体开裂和分层损伤因子的计算公式为

式中：J是面内近场域中纤维方向物质点总数；是面内近场域中非纤维方向物质点总数；是面外近场域中上层方向物质点总数；是面外近场域中下层方向物质点总数。

2 复合材料低速冲击近场动力学模拟刚度验证

采用近场动力学模拟图2 所示圆形板冲击过程，不考虑复合材料的损伤，来验证常规态近场动力学复合材料球型域模型在冲击载荷作用下的刚度可靠性。该算例中被冲击板的直径为75 mm，厚度为2 mm，铺层为[0/90]2s，单层厚度为0.25 mm，相应的复合材料的材料参数如表1 所示。冲击小球的直径为15 mm，质量为0.5 kg，初速度为1 m/s，初速度垂直于板面，圆形板外圆周面固支。

表1 复合材料圆形板材料参数Table 1 Composite circular laminate material parameters

图2 复合材料低速冲击刚度验证示意图Fig.2 Composite low-velocity impact stiffness validation diagram

近场动力学计算量较大，为提高计算效率，采用1/4 模型进行计算。近场动力学计算的复合材料层合板在冲击载荷作用下的变形云图如图3所示。近场动力学(PD)和有限元(FEM)计算冲击过程冲击力随时间的变化如图4 所示，冲击小球速度随时间的变化如图5 所示，冲击小球位移随时间的变化如图6 所示，可以看到，PD 和FEM计算的结果吻合得很好。可见采用常规态近场动力学复合材料球型域模型模拟复合材料低速冲击过程，模型刚度准确可靠。

图3 复合材料低速冲击刚度验证变形云图Fig.3 Deformation cloud for low velocity impact of composite

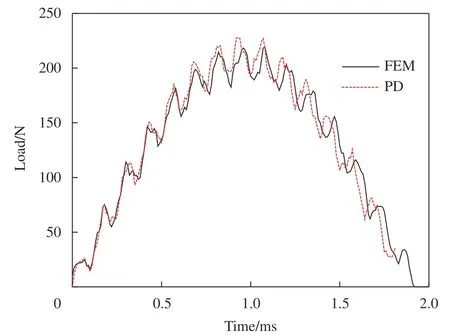
图4 复合材料低速冲击刚度验证冲击力-时间曲线Fig.4 Low velocity impact load-time curves of composite

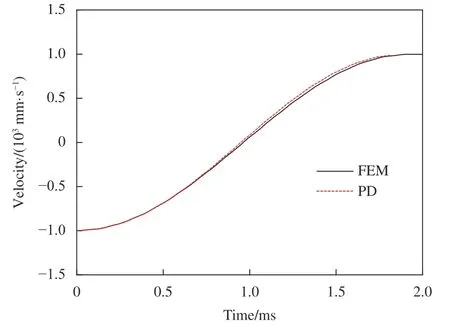
图5 复合材料低速冲击刚度验证冲击速度-时间曲线Fig.5 Low velocity impact velocity-time curves of composite

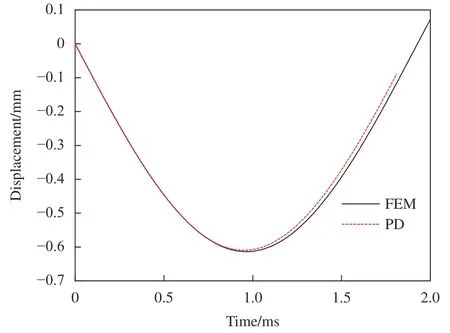
图6 复合材料低速冲击刚度验证冲击位移-时间曲线Fig.6 Low velocity impact displacement-time curves of composite

3 复合材料低速冲击近场动力学损伤模拟

图7 为复合材料低速冲击损伤模拟示意图，其试验数据取自文献[25]，被冲击板长125 mm，宽75 mm，厚度为4.16 mm，铺层为[02/452/902/-452]s，单层厚度为0.26 mm，相应的复合材料的材料参数如表2、表3 所示。冲击小球的直径为16 mm，质量为2 kg，初速度为2.55 m/s，初速度垂直于板面。

表2 碳纤维增强环氧树脂复合材料(T700/M21)的面内材料性能[25]Table 2 In-plane material parameters of carbon fiber reinforced epoxy resin composite (T700/M21)[25]ρ=1 580 kg/m3

表3 T700/M21 复合材料面外材料性能[25]Table 3 Out-plane material parameters of T700/M21[25]

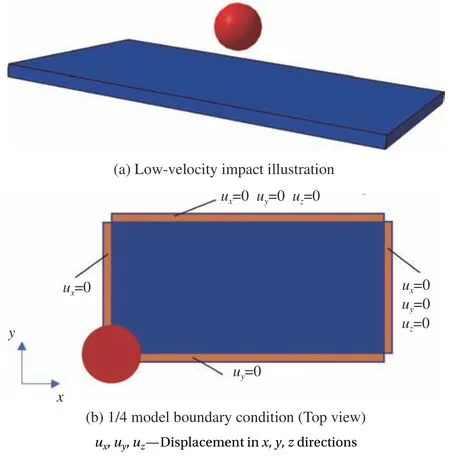
图7 复合材料低速冲击损伤模拟示意图Fig.7 Schematic diagram of low velocity impact damage simulation of composite

近场动力学计算的复合材料低速冲击损伤模拟的冲击力-时间曲线如图8 所示，可以看到，相比于不带损伤的有限元(FEM_NoDamage)和近场动力学(PD_NoDamage)结果，考虑损伤情况下复合材料层合板冲击力-时间曲线(PD_Damage)有明显下沉，最大冲击载荷减小，整个冲击下降回弹过程时间变长。

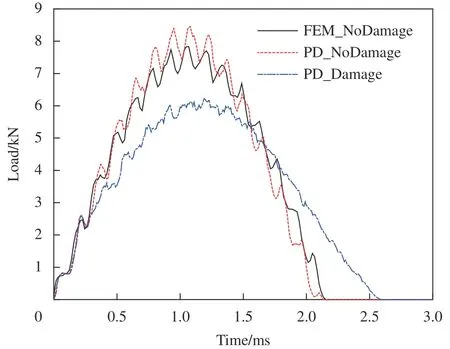
图8 复合材料冲击损伤模拟冲击力-时间曲线Fig.8 Low velocity impact damage modeling load-time curves of composite materials

图9、图10 和图11 给出了复合材料低速冲击损伤模拟在不同时间步每一层的分层损伤、纤维断裂和基体开裂。可以看到该复合材料层合板在低速冲击载荷作用下，主要发生分层损伤和基体开裂这两种失效模式。分层损伤和基体开裂随着冲击力的增大而扩展(0.5～1.5 ms)，而当冲击小球回弹，冲击力减小以后，分层损伤和基体开裂几乎不再扩展(1.5～3 ms)。

图9 复合材料低速冲击损伤模拟每一层的分层损伤随冲击时间的变化Fig.9 Delamination variation of composite each ply under low-velocity impact with time

图10 复合材料低速冲击损伤模拟每一层的纤维断裂随冲击时间的变化Fig.10 Fiber breakage variation of composite each ply under low-velocity impact with time

图11 复合材料低速冲击损伤模拟每一层的基体开裂随冲击时间的变化Fig.11 Matrix crack variation of composite each ply under low-velocity impact with time

复合材料低速冲击损伤模拟分层形状对比如图12 所示，近场动力学模拟的分层形状是每一层分层损伤的包络图，可以看到，近场动力学模拟出了半弧状的分层损伤，与试验C 扫分层形状较吻合。表4 给出了分层面积的比较，近场动力学的1/4 模型模拟的分层面积为93.56 mm2，从而近场动力学模拟的整块复合材料层合板的分层面积为374.24 mm2，与试验分层面积312.3 mm2相比，误差为+19.8%，该误差量级在工程可接受的范围内。文献[25]中基于有限元方法，对上述低速冲击过程采用粘接单元来模拟层间分层，模拟得到的分层面积为358.1 mm2(+14.7%)，与本文采用近场动力学模拟的误差在同一个量级上。值得说明的是，近场动力学模拟不需要像粘接单元一样预制裂纹扩展路径，且基于能量的损伤判定准则，只需要输入材料的断裂韧性，不存在粘接元刚度等的可调参数，此外近场动力学的计算较容易收敛。

表4 复合材料低速冲击损伤模拟分层面积比较Table 4 Delamination area comparison of composite under low-velocity impact

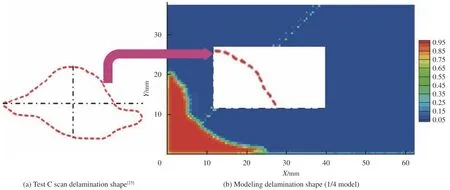
图12 复合材料低速冲击损伤模拟分层形状对比Fig.12 Delamination shape comparison of composite under low-velocity impact

4 结 论

近场动力学模拟复合材料层合板低速冲击损伤具有一定优势，本文在球型域常规态近场动力学复合材料模型基础上，建立了考虑时间步长下不同断裂混合比的能量失效判定准则，并开展了基于能量准则的复合材料层合板低速冲击近场动力学模拟。结果表明：

(1) 近场动力学模拟的复合材料低速冲击冲击接触力、冲击速度及冲击位移与有限元结果具有较好的一致性，近场动力学复合材料低速冲击模拟刚度可靠；

(2) 近场动力学模拟复合材料低速冲击损伤结果表明，考虑损伤情况下复合材料层合板冲击力-时间曲线有明显下沉，最大冲击载荷减小，整个冲击下降回弹过程时间变长；

(3) 近场动力学能够模拟复合材料低速冲击过程中层合板纤维断裂、基体开裂及分层损伤扩展过程，典型复合材料层合板在低速冲击载荷作用下，主要发生分层损伤和基体开裂这两种失效模式。分层损伤和基体开裂随着冲击力的增大而扩展(0.5～1.5 ms)，而当冲击小球回弹，冲击力减小以后，分层损伤和基体开裂几乎不再扩展(1.5～3 ms)；

(4) 近场动力学基于能量准则模拟的分层损伤面积和分层形状与试验结果具有较好的一致性，验证了所建立的考虑时间步长下不同断裂混合比的能量失效判定准则的有效性。