单元整体教学理念下单元起始课的设计与实施策略

郑琳琳

初中数学单元整体教学实施的前提是教师充分了解学生，解读教材，分析前后知识之间的关联，把握前后知识的迁移和转化规律，再对比学生已有的知识体系，从整体上构建教学目标和内容，系统落实教学活动。这样教学有利于培养学生的数学核心素养，帮助学生构建结构化的数学知识体系，形成研究一类数学问题的通理、通法。在单元整体教学理念的引领下，笔者认真研究了人教版数学八年级第十四章《整式的乘法》内容，以第一课时《单项式与单项式相乘》的教学为例，阐释单元整体教学理念下单元起始课的设计与实施策略。

一、以整体视角引入学习，明确学习路径

课堂上，笔者先提问：“在七年级，我们已经学习了整式的加法，你认为还需要研究整式的什么运算呢？”学生很容易通过数的运算联想到要进行整式的乘除法运算。接着，笔者要求学生解决问题1，并猜测一下整式乘法有哪几种类型。

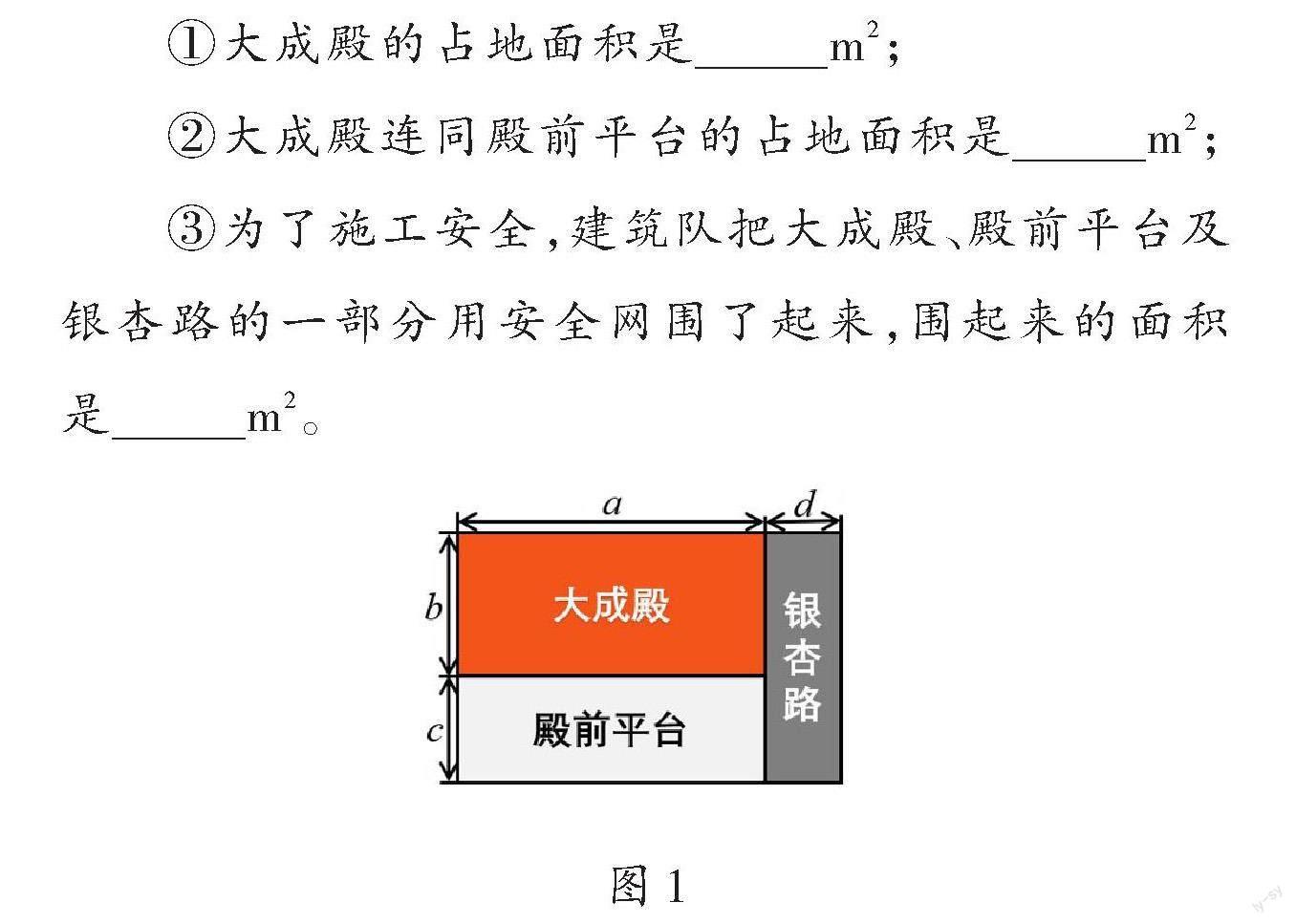
问题1：大成殿是湖北省重点保护文物，襄阳市文物保护管理处会定期对大成殿进行修缮，相关数据如图1所示，请列式表示（单位：m）：

①大成殿的占地面積是     m2；

②大成殿连同殿前平台的占地面积是     m2；

③为了施工安全，建筑队把大成殿、殿前平台及银杏路的一部分用安全网围了起来，围起来的面积是     m2。

学生作答后发现：整式乘法的类型有单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘。笔者引导：“今天我们学习单项式与单项式相乘。回顾整式加法中同类项的内容，我们是从特殊的数的运算入手，研究一般的式的运算。本节课，我们类比这一过程，研究单项式与单项式相乘。”随后，笔者对引例中的单项式与单项式相乘进行处理，赋予数值后形成“（1.8×103）×（1.1×103）”算式。学生运用已有知识解决问题后，笔者追问学生在计算过程中用到了哪些运算律及运算性质。有的学生回答乘法交换律和乘法结合律，有的学生回答幂的运算，即同底数幂的乘法，这正是单项式与单项式相乘计算法则的依据。

这样引入，学生了解了整个单元要学习的内容，明确学习新知可以借助已有知识和经验，可以类比相似内容的学习路径，有利于学生整合新旧知识，尝试建构更完整的数学知识体系。

二、设计有层次的问题，合作探究运算的一般方法

本环节，笔者结合法则的形成过程，设置有层次的问题，引导学生合作探究，最终解决问题。在探讨单项式与单项式相乘的法则时，笔者通过有层次的问题，引导学生由特殊到一般地理解运算法则，形成运算的一般方法。笔者先将“（1.8×103）×（1.1×103）”一般化为“1.8c3·1.1c3”，让学生对比两种运算有什么相似之处。学生通过计算，从运算律和运算性质两个方面回答了笔者提出的问题。接着，笔者让学生说一说单项式与单项式相乘应该怎样计算。有的学生说“要先把有理数相乘，再把同底数幂相乘”，有的学生说“因为是单项式与单项式相乘，应该先把系数相乘，再把同底数幂相乘”。对于学生的解题思路，笔者没有马上回应，而是继续对乘法算式进行一般化处理，呈现“1.8c3·1.1b2c3”，让学生小组讨论上一个算式与这个算式在计算时有什么区别和联系。学生思考后回答：“相同点是1.8c3和1.1c3仍然要相乘，不同点是这个算式中的第二个因式中多了一个b2。”笔者追问：“你能对单项式与单项式相乘的计算方法进行补充吗？回顾这几个实例，你能谈一谈单项式与单项式相乘的一般步骤吗？”交流讨论之后，学生回答：“首先是把系数相乘，同底数幂相乘，然后是把只在一个单项式中含有的字母连同指数作为积的一个因式。” 这样教学，学生在观察、讨论、概括中总结出单项式与单项式相乘这一运算的本质特征，体会到数的运算与式的运算的通理、通法，形成了从特殊到一般的研究运算法则的方法，巩固了类比和转化的数学思想。

三、梳理知识结构图，总结学习式运算的方法与路径

课堂小结环节，笔者让学生回顾知识内容，总结研究问题的方法，形成知识结构图（如图2），以把握学习式运算的整体脉络，并通过知识结构图明确接下来的学习内容和研究方向。

知识结构图把本节课的内容（单项式与单项式相乘的法则）、研究的依据（运算律和幂的运算）、使用的方法（类比和转化）、以后要研究的内容有机联系起来，让学生进一步体悟从数到式、由特殊的到一般的研究过程，了解研究这类式的运算都要从特殊的数出发，为后续学习提供了方法和路径指导。

（作者单位：襄阳市第五中学附属初级中学）

责任编辑  刘佳