风电虚拟惯量延时的影响机理模型解析及替代性研究

2024-04-22张峰，田宇，丁磊

电力系统自动化 2024年7期

张峰，田宇，丁磊

（电网智能化调度与控制教育部重点实验室（山东大学），山东省济南市250061）

0 引言

随着“碳达峰·碳中和”目标的提出，新能源发电受到越来越多的重视。然而，新能源发电通过电力电子设备并网，转子转速与电网频率解耦特性使其无法像同步机一样自发响应系统频率变化［1-2］。在新能源渗透率不断提高的背景下，电网的频率安全性将会受到严峻的挑战［3］。

为应对新能源渗透率提高导致的电网频率安全性降低的问题，国内外电网运行导则均规定并网运行的风电机组需具备响应电网频率变化的能力［4-5］。已有文献也提出了多种风电调频策略，主要有功率备用［6-7］和利用转子动能［8-9］两种模式。相比于功率备用模式，利用转子动能的模式可以使风电机组运行在最大功率点跟踪（maximum power point tracking，MPPT）模式，经济性更好。因此，本文主要研究利用转子动能的调频模式。目前，利用转子动能的风电调频策略主要有综合惯性控制［10］、虚拟同步机控制［11］和变锁相环控制［12］。其中，综合惯性控制原理清晰、简单易行，是本文的主要研究对象。综合惯性控制通过对风电机组转子侧变流器的功率控制环节进行改进，在原有功率指令上附加调频功率，进而改变变流器的功率参考值，其主要包括虚拟惯量控制［13-14］和下垂控制［15-16］。其中，虚拟惯量控制使用频率变化率作为输入信号，旨在模拟同步机的惯量响应；下垂控制使用频率偏差作为输入信号，旨在模拟同步机的一次调频。

然而，与同步机零延时的惯量响应不同，风电机组采用虚拟惯量控制参与电网调频时本质上是快速功率响应，固有测频、通信环节，故此过程存在一定延时［17］。为保障频率微分量测的准确性，虚拟惯量控制一般需要5～10 个工频周期的测频时间，再兼顾通信延时，其固有延迟时间可达300 ms［18-20］。然而，目前对虚拟惯量延时特性的研究较少，延时对系统频率动态的影响机理尚不清晰，需要对虚拟惯量延时特性展开建模分析。此外，虚拟惯量存在测频精度需求高、频率微分环节放大量测误差等固有缺陷，相较下垂控制可靠性较差，并且上述缺陷导致虚拟惯量一般具有比下垂控制更长的功率响应延时。因此，为规避虚拟惯量的不足之处，文中探究了风电调频使用下垂控制替代虚拟惯量控制的可行性。

针对上述问题，本文在解析求解考虑风电机组虚拟惯量延时特性的系统频率响应（system frequency response，SFR）模型的基础上，研究风电调频使用下垂控制替代虚拟惯量控制的可行性。具体而言，基于对风电机组虚拟惯量控制和下垂控制延时特性的分析，建立了包含风电机组与常规同步机组的SFR 模型，基于劳斯（Routh）近似法解析求解风电调频分别使用综合惯性控制与仅使用下垂控制时的频率最低点。然后，在风电调频使用两种控制方式频率最低点相等的前提下，给出风电调频仅使用下垂控制时的系数设定方法。进一步，分析得出在设定下垂控制系数下，风电机组能够在仅使用下垂控制时实现替代虚拟惯量控制的目的，并能取得比使用综合惯性控制时更佳的调频效果。最后，搭建了包含常规同步机组与风电机组的两区域模型，验证了本文分析的正确性。

1 虚拟惯量延时特性建模及系统频率解析

建立了考虑延时环节的SFR 模型。针对高阶模型难以求得时域解析解的问题，基于Routh 近似法实现对高阶模型的降阶及系统频率动态解析求解，并基于系统频率关键指标解析表达式分析了延时对系统频率动态的影响，为虚拟惯量的可替代性分析提供了理论基础。

1.1 风电虚拟惯量延时特性建模

风电机组通过电力电子设备并网，转子转速与电网频率解耦，使其无法自发响应系统频率变化。因此，若期望风电机组参与电网频率调整，则需对其变流器功率控制环节附加功率控制模块，其控制结构框图如附录A 图A1 所示，调频原理如下。

正常运行时，风电机组工作在MPPT 模式下。当系统频率f偏离频率额定值f0后，风电机组采用综合惯性控制参与电网调频。综合惯性控制通过对变流器控制策略进行改进，将频率变化率和频率偏差信号引入变流器功率控制环节，在风电机组原本的功率指令上增加一个附加功率ΔP，附加功率的大小与频率变化率及频率偏差成正比。其中，附加功率中与频率变化率成正比的被称作虚拟惯量控制，附加功率中与频率偏差成正比的被称作下垂控制，综合惯性控制是虚拟惯量控制和下垂控制的结合。表达式为:

式中:ΔP为风电机组综合惯性控制附加调频功率；Δf为系统频率偏差；kd为虚拟惯量控制系数；kp为下垂控制系数。

然而，与同步机零延时的惯量响应不同，风电机组采用综合惯性控制参与电网调频的本质是快速功率响应，存在以下环节所需时间:

1）测频时间:从电网中测量得到频率变化率及频率偏差信号所需时间。

2）通信时间:将测量得到的系统频率信号传递给风电机组转子侧变流器功率控制环节所需时间。

3）响应时间:从风电机组得到功率指令到响应至额定功率所需时间。

上述均是风电机组功率响应过程中存在的延时环节。计及延时环节，风电机组参与电网调频时的功率响应原理如附录A 图A2 所示。实际中，虚拟惯量为保障频率微分量测的准确性，通常具有比下垂控制更长的测频时间，但可以通过改进测频方法，使两者实际测频时间相差较小［21-22］。本文为简化分析需要，认为当风电调频使用综合惯性控制时，其下垂控制功率响应延时与虚拟惯量控制一致，故可用虚拟惯量延时代表风电机组功率响应延时。进一步，将延时环节近似等效为一阶惯性环节［23］，简化后风电机组功率响应表达式为:

式中:ΔPwind为调频期间风电机组实际输出调频功率；Td为风电机组虚拟惯量控制功率响应延时的等效时间常数；s为拉普拉斯算子。

由式（2）可知，调频期间风电机组实际输出调频功率的大小由虚拟惯量控制系数和频率变化率信号、下垂控制系数和频率偏差信号共同决定，而功率响应的时间则取决于延时大小。由此可见，延时主要影响了风电机组调频功率的响应时间，进而影响了系统频率动态。

为分析延时对系统频率动态的非线性影响机理，文中在经典SFR 模型的基础上加入了风电机组功率控制环节［24-26］，建立了考虑风电机组功率响应延时的SFR 模型，如图1 所示。图中:ΔPL为扰动功率；ΔPG为系统一次调频响应功率；α为风电渗透率水平；M为系统惯性时间常数；D为系统阻尼系数；FH为系统汽轮机高压缸做功比例；TR为系统再热时间常数；R为系统一次调频调差系数。

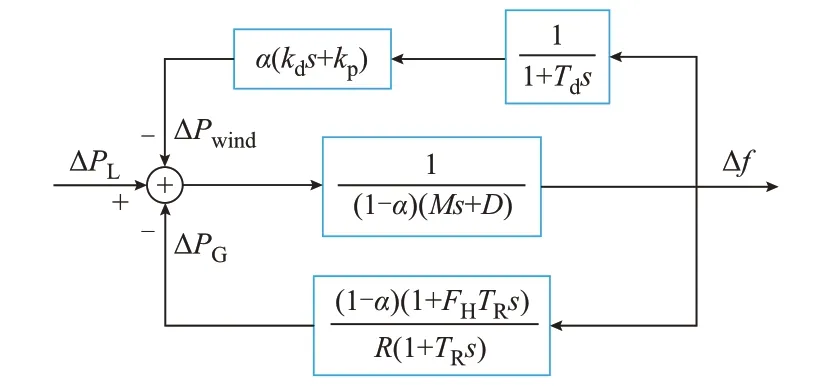
图1 风电机组参与电网调频的SFR 模型Fig.1 SFR model of wind turbine generators participating in power grid frequency regulation

风电机组在调频期间采用综合惯性控制，同时兼顾了风电渗透率水平及风电机组功率响应延时。

基于SFR 模型可得系统传递函数G(s)为:

经化简可得:

式中

考虑到电力系统中阶跃形式的扰动最常见且影响最大，如发电机切机、负荷突增等，本文假设系统扰动功率ΔPL为阶跃形式。当发生扰动时，系统频率响应表达式ΔfZ(s)为:

由式（4）和式（5）可得，考虑延时特性的系统频率响应模型具有高阶特征，难以直接求其时域解析解。为此，后续将基于Routh 近似法实现高阶模型的降阶及时域求解［27］。

1.2 基于Routh 近似的系统频率最低点解析求解

由式（4）可知，考虑延时特性时SFR 模型为三阶，传递函数特征方程为三阶参数方程。然而，三阶参数方程无法解析求解，使得系统模型无法时域解析，进而也无法得到系统频率动态的解析表达式。为此，文中使用Routh 近似法对系统模型进行降阶，得到降阶模型传递函数R(s)为:

式中

由式（5）可得，降阶模型系统频率响应表达式为:

对式（7）进行拉普拉斯反变换，可求得系统频率响应表达式时域形式Δf(t)为:

式中

令系统频率响应微分等于零，即可求得到达频率最低点的时间。首先，求得系统频率响应微分:

可以看出，当式（9）右侧括号中三角函数项为零时，系统频率响应微分为零。因此，可求得到达频率最低点的时间tm为:

式（10）中，k值需参考-φ和arctan(-δ/Ω)的角度，若两者角度和在二、三象限，则k值取1，否则取0。将式（10）代入式（8），即可得到系统频率最低点Δfmax表达式为:

由式（11）可知，在系统的常规同步机组参数M、D、FH、TR、风电渗透率水平α及系统扰动ΔPL大小已知的情况下，系统频率最低点Δfmax由风电机组的虚拟惯量控制系数kd、下垂控制系数kp及延时Td决定。文中将借助表达式进一步阐述延时对系统频率动态的影响机理。

1.3 虚拟惯量延时对系统频率动态的影响

目前，评价电力系统发生有功扰动后频率响应优劣的指标主要有3 个:系统频率最低点Δfmax、最大频率变化率和稳态频率Δfset。因此，下文基于系统频率响应指标，研究延时对系统频率动态的影响机理。

前文已求得系统频率最低点解析表达式，如式（11）所示；系统频率最大变化率及稳态频降可分别通过拉普拉斯变换初值定理与终值定理求得［28］，如式（12）和式（13）所示。

分析式（12）可得，当不考虑延时特性时，虚拟惯量能够在扰动初始时刻分担扰动功率，使得最大频率变化率随着虚拟惯量系数的增大而减小，实现了同步机惯量支撑的作用。然而考虑延时特性时，虚拟惯量不具备在扰动初始时刻分担扰动功率的能力，其本质是带延时的快速功率响应。此时，系统最大频率变化率与延时大小无关。

分析式（13）可得，稳态频率仅与扰动大小、同步机调差系数、风电渗透率水平、同步机阻尼系数及风电机组下垂控制系数有关，与延时大小无关。

延时对系统最大频降的影响可通过对式（11）分析得到。由式（11）可知，在系统的常规同步机组参数、扰动大小及风电渗透率已确定的情况下，最大频降由风电机组的调频参数kd、kp及虚拟惯量功率响应延时Td决定。因此，将表达式中与风电机组调频参数无关的变量赋典型值［29］，即同步机参数:M=10 s，D=1。调速器参数:R=0.05，TR=10 s，FH=0.3。风电渗透率:α=0.3。扰动:ΔPL=0.1 p.u.。在此基础上，分析得到系统频率最低点会随延时增大而降低的结论，如图2 所示。

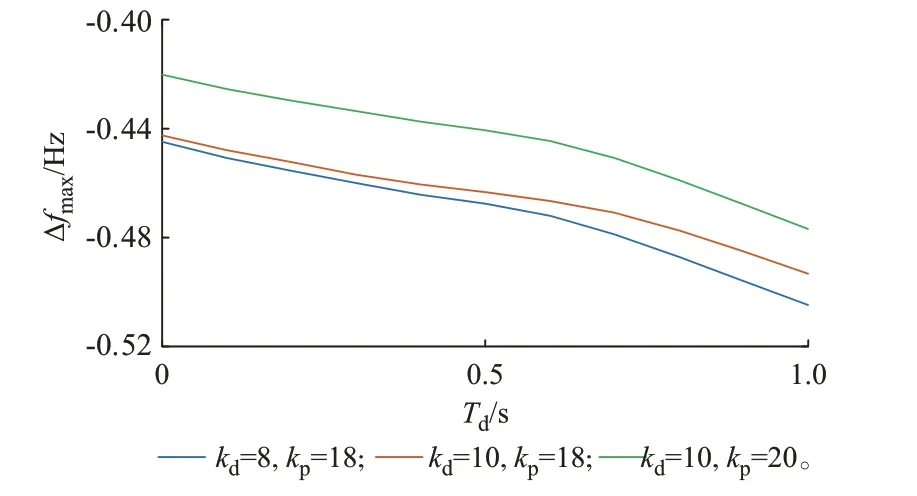
图2 延时对系统频率最低点的影响Fig.2 Influence of time delay on system frequency nadir

综上可得，延时Td对系统最大频率变化率及稳态频率无影响，而系统频率最低点会随着延时的增大而降低。

由此可见，考虑延时特性时，虚拟惯量控制不能在扰动初始时刻分担扰动功率，因为与同步机的惯量响应不同，其本质是带延时的快速功率响应，与下垂控制一致。与此同时，虚拟惯量控制存在测频精度需求高且频率微分环节存在放大量测误差等固有缺陷，相比于下垂控制其可靠性较差，且上述缺陷导致虚拟惯量控制一般具有比下垂控制更长的功率响应延时。因此，为规避虚拟惯量控制的不足之处，文中探究风电机组使用下垂控制替代虚拟惯量控制的可行性。

2 带延时虚拟惯量的可替代性研究

解析求解得到风电调频仅使用下垂控制时的系统频率最低点表达式，基于系统频率最低点指标给出下垂控制系数设定方法，并聚焦于最大频率变化率、稳态频率指标，分析了使用下垂控制替代带延时虚拟惯量的可行性。

2.1 带延时下垂控制时的系统频率最低点解析

文中主要研究利用转子动能的调频模式，故风电机组基于桨叶转子动能提供下垂控制。由前文分析可知，虚拟惯量为保证频率微分量测的准确性，一般具有比下垂控制更长的测频时间。因此，当虚拟惯量和下垂控制能源均来自桨叶动能时，下垂控制功率响应延时小于虚拟惯量。由式（2）可得，风电调频仅使用下垂控制时的功率响应表达式为:

式中:ΔP′wind为调频期间风电机组仅使用下垂控制时的实际输出调频功率；k′p为风电调频仅使用下垂控制时的调频系数；T′d为下垂控制延时的等效时间常数；Δf′为风电调频仅使用下垂控制时的系统频率偏差值。

参照1.1 节，对于风电机组仅使用下垂控制参与电网调频时的系统模型，可通过将图2 所示SFR模型中风电机组功率响应反馈通道的传递函数替换为式（14）得到。由此可见，风电调频仅使用下垂控制时的系统模型可通过将其使用综合惯性控制时的系统模型通过式（15）置换得到。

同理可得，风电调频仅使用下垂控制时的系统传递函数G′(s)及系统频率响应表达式Δf′(s)为:

分析式（16）可得，风电调频仅使用下垂控制时的系统模型为三阶。因此，解析求解系统频率响应表达式时，仍需借助Routh 近似法对其进行降阶处理。进而，得到降阶模型传递函数R′(s)为:

参照式（7）—式（11），风电机组仅使用下垂控制参与电网调频时，系统频率最低点解析表达式Δf′max为:

需要指出的是，由于调频初期系统频率偏差较小，下垂控制功率支撑作用不明显，导致当风电机组仅使用下垂控制参与电网调频时，调频初期系统频率跌落速度较使用综合惯性控制时加快，进而导致到达频率最低点的时间提前。

2.2 下垂控制系数设定方法及替代性分析

1）基于频率最低点等效的下垂系数设定方法

由于发生有功扰动后，系统频率最低点代表了系统频率受扰动后影响程度最大的情况，是评价系统频率安全性的重要指标。因此，文中以系统频率最低点为指标，研究当风电调频分别在仅使用下垂控制和使用综合惯性控制且系统频率最低点相等时的下垂控制系数设定方法。当风电调频分别在使用两种控制方式且系统频率最低点相等时，满足以下关系:

通过式（20）可得，两种控制方式之间调频参数替代关系为:

两种控制方式调频参数之间的替代关系如附录A 图A3 所示。

由式（20）可知，在系统的常规同步机组参数、风电渗透率水平、系统扰动及延时大小已知的情况下，系统频率最低点只由风电机组的调频参数kd、kp、k′p决定。由于替代前后系统频率动态存在差异，导致在式（21）所示的替代关系中含有大量的三角函数项及指数项，无法解析表达替代后下垂控制系数与替代前虚拟惯量系数和下垂控制系数之间的关系。因此，文中使用数值法求解并将数值解采用三维坐标图的形式表达，说明替代前后风电机组调频参数之间存在的替代关系。

将系统频率最低点表达式中与风电机组调频参数kd、kp无关的变量赋典型值，详见文中1.3 节。同时，将风电调频虚拟惯量控制功率响应延时取为Td=500 ms，仅使用下垂控制时功率响应延时取为T′d=400 ms。风电机组的调频控制参数取值范围设置为［5］:kd∈[8，12]，kp∈[15，25]。求解得到当风电调频仅使用下垂控制时的系数设定方法如图3 所示。图中:x、y轴分别表示风电调频使用综合惯性控制时的虚拟惯量系数kd及下垂控制系数kp；z轴表示风电调频仅使用下垂控制时的系数k′p。

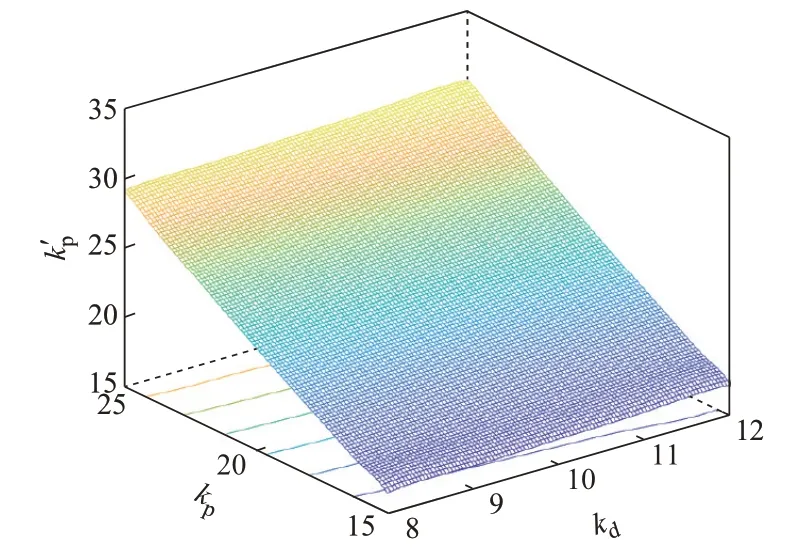
图3 下垂控制系数设定Fig.3 Setting of droop control coefficients

2）基于频率动态关键指标的替代可行性分析

本节聚焦于系统频率动态关键指标（频率最低点、最大频率下降率、稳态频率），分析使用下垂控制替代虚拟惯量控制的可行性。考虑到文中下垂控制系数设定方法是通过令风电调频仅使用下垂控制时与使用综合惯性控制时系统频率最低点相等所得到的，只需分析替代前后对最大频率变化率及稳态频率的影响。

首先，求解风电调频仅使用下垂控制时的最大频率变化率及稳态频率偏差，分别如式（22）和式（23）所示。

对比式（12）和式（22）可得，考虑延时特性时系统最大频率变化率与风电机组调频控制参数无关。因此，风电调频仅使用下垂控制与使用综合惯性控制时的系统最大频率变化率相同。对比式（13）和式（23）可得，系统稳态频率偏差与风电机组下垂控制系数kp呈负相关，kp越大则稳态频率偏差越小、稳态频率越高。由图3 可知，当风电调频仅使用下垂控制时，为取得和使用综合惯性控制时相同的频率最低点，需适当增大下垂控制系数。因此，当风电调频仅使用下垂控制时较使用综合惯性控制时的稳态频率有所提高。

综上，文中基于系统频率最低点指标给出的下垂控制系数设定方法，不仅能取得与使用综合惯性控制时相同的频率最低点及最大频率变化率，而且能提高系统稳态频率。由此可见，风电机组仅使用下垂控制参与电网调频时，通过适当增加下垂控制系数能够实现替代虚拟惯量控制的目的，并能取得比使用综合惯性控制时更佳的调频效果。

3 算例分析

为验证延时影响机理模型分析的准确性，以及所提下垂控制系数设定方法的可行性，在MATLAB/Simulink 仿真平台搭建了包含常规同步机组与风电机组在内的两区域系统仿真模型。仿真结构如附录A 图A4 所示，常规同步机组与风电场运行参数分别如附录A 表A1 和表A2 所示。

3.1 虚拟惯量特征及延时影响仿真验证

3.1.1 虚拟惯量特征分析

如前文所述，虚拟惯量微分环节易对频率量测误差产生放大作用，且风电调频延时特性对风电机组响应功率产生不利影响。设置仿真参数如下:风电场初始风速设置为15 m/s，风电场出力30 MW，系统初始有功负荷103 MW，风电机组调频参数为kd=10，kp=20。假设系统在40 s 时发生6 MW 的负荷突增事件，系统频率动态及其微分信号仿真曲线如附录A 图A5 所示。

由于风电机组虚拟惯量控制输出功率与系统频率微分成正比，而微分环节存在测量精度需求高、放大量测误差等问题，在系统频率出现振荡时影响尤为严重。通过仿真曲线可知，系统频率微分信号中存在许多波动信号，放大量测误差作用明显。

3.1.2 延时对风电机组功率响应及系统频率动态影响

为验证延时对风电机组功率响应及系统频率动态的影响，设置仿真参数与3.1.1 节一致，并在延时大小分别为0.2、0.5、1.0 s 三种情况下，分析延时对风电机组虚拟惯量控制与下垂控制响应功率及其对系统频率动态的影响。仿真曲线如图4 所示。

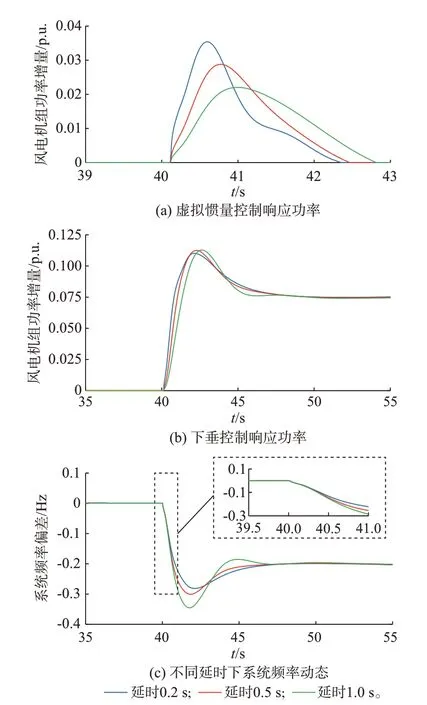
图4 延时对风电机组功率响应及系统频率动态影响Fig.4 Influence of time delay on power response of wind turbine generators and system frequency dynamics

虚拟惯量控制旨在模拟同步机瞬时的惯量响应，在扰动初始时刻分担扰动功率使输出功率突变。然而，虚拟惯量控制本质是带有延时的功率响应，由于延时的存在，其不能在扰动初始时刻提供瞬时功率支撑，同时虚拟惯量控制响应功率的幅值随着延时的增大而减小，如图4（a）所示。而下垂控制旨在模拟同步机的一次调频，其响应功率与频率偏差成正比，在系统频率最低点附近能够提供较强支撑，无论延时大小，其均能在系统频率最低点附近提供较强支撑，如图4（b）所示。

当系统发生负荷突增事件后，风电机组通过虚拟惯量与下垂控制提供调频功率响应电网频率变化。然而，此过程是存在一定延时的功率响应，延时主要影响了调频期间风电机组调频功率响应时间，使得频率最低点随着延时的增大而降低，如图4（c）所示。系统最大频率变化率发生在扰动初始时刻，由于延时的存在，虚拟惯量控制不能在扰动初始时刻分担扰动功率使输出功率突变，因而系统最大频率变化率与延时大小无关，如图4（c）所示。同时，由图4（c）可知，系统的稳态频率也与延时大小无关。

可见，延时对系统频率动态存在不利影响，其主要影响系统频率最低点，且延时越大，系统频率最低点越低，故需要进行机理模型构建及量化分析。

3.2 基于Routh 近似法降阶的有效性验证

该验证部分通过对比模型降阶方法得到的系统频率最低点解析表达式和基于SFR 模型时域仿真得到的结果，验证通过模型降阶方法得到的系统频率最低点解析表达式的有效性。

首先，验证不同延时下模型降阶方法的有效性。在风电机组功率响应延时大小不同的情况下，通过模型降阶方法解析求解得到的系统频率最低点与通过SFR 模型时域仿真法得到的频率最低点对比如图5（a）所示。可见，两者得到的结果十分相近，最大误差不超过0.035 Hz，误差小于10%。因此，通过模型降阶法得到的系统频率最低点解析表达式有效。然后，研究不同风电机组调频参数下模型降阶法的有效性。风电机组的调频控制参数取值范围设置为:kd∈[8，12]，kp∈[15，25]，风电机组功率响应延时取为Td=500 ms。在不同风电机组调频参数下，通过模型降阶方法解析求解得到的系统频率最低点与通过SFR 模型时域仿真法得到的系统频率最低点误差如图5（b）所示。可见，两者得到的结果十分相近，最大误差不超过0.055 Hz，误差小于15%。因此，通过模型降阶法得到的系统频率最低点解析表达式有效。

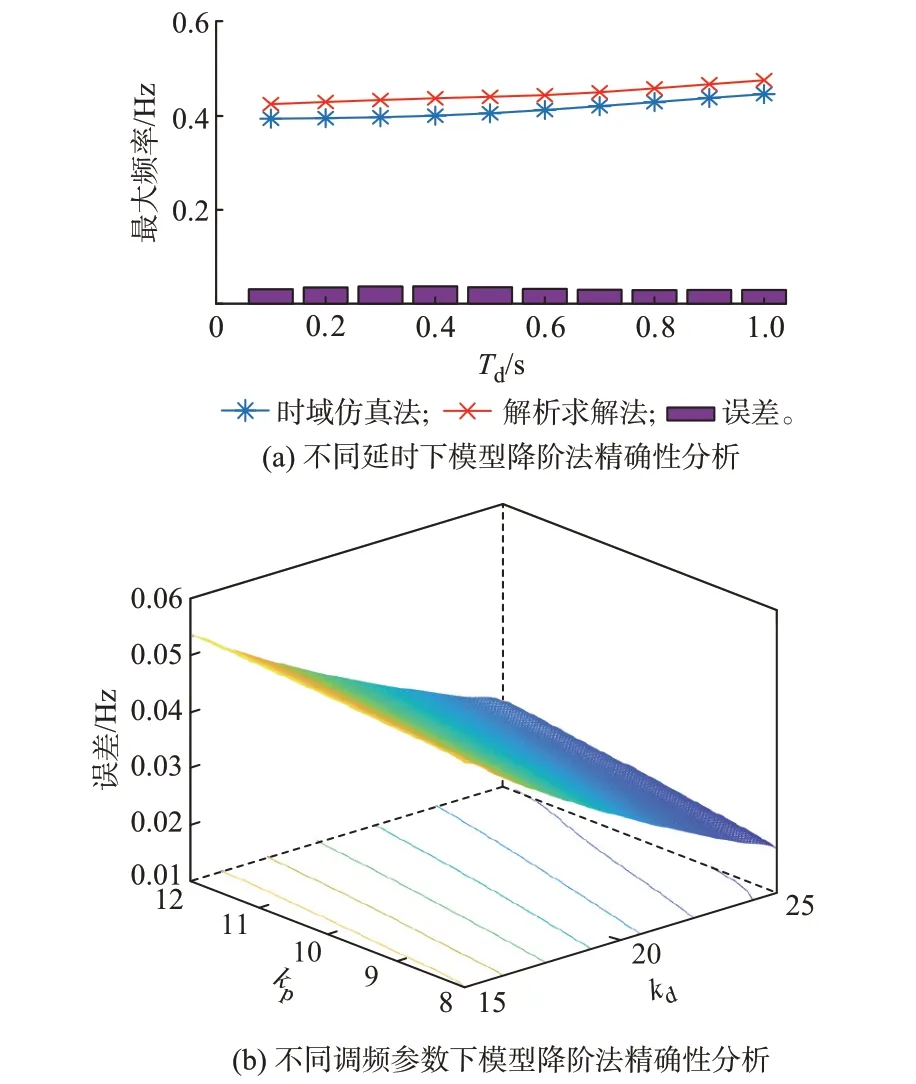
图5 模型降阶法精确性分析Fig.5 Accuracy analysis of model reduction method

由此可见，当系统模型具有高阶特征难以对其进行解析求解时，通过模型降阶法对高阶系统模型进行降阶，然后对降阶模型进行解析求解是有效的。

3.3 下垂控制系数设定方法有效性及替代可行性验证

3.3.1 不同场景下的下垂控制系数设定方法验证

为验证文中所提下垂控制系数设定方法在不同场景下的适用性，本节使用附录A 表A1 和表A2 所示的仿真模型参数，在不同风电渗透率场景下求解风电调频仅使用下垂控制时的调频参数。风电机组出力分别设置为30 MW 和45 MW，得到下垂控制系数设定方法如附录A 图A6 所示。可见，在不同风电渗透率场景下，文中基于系统频率最低点指标给出的下垂控制系数设定方法均可适用。同时，对比风电渗透率不同时所得到的下垂控制系数可以看出，随着风电渗透率的增加，由于系统的惯量水平降低，当发生相同负荷扰动时系统跌落速度加快。为取得与综合惯性控制相同的系统频率最低点，需要增加更多的下垂控制系数。

由此可见，在不同的风电渗透率场景下，均可基于文中给出的下垂控制系数设定方法，得到与风电机组使用综合惯性控制时频率最低点相同的下垂控制系数。

3.3.2 带延时虚拟惯量的可替代性仿真验证

为验证文中风电机组使用下垂控制替代虚拟惯量控制的可行性，设置仿真参数如下:假设风电调频使用综合惯性控制时的调频参数为kd=10 、kp=20，其他参数与3.1.1 节仿真参数一致，求得当风电调频仅使用下垂控制时的调频参数为k′p=24.49。进一步，得到风电调频分别在仅使用下垂控制和使用综合惯性控制时的仿真曲线如图6 所示，频率响应指标对比如表1 所示。

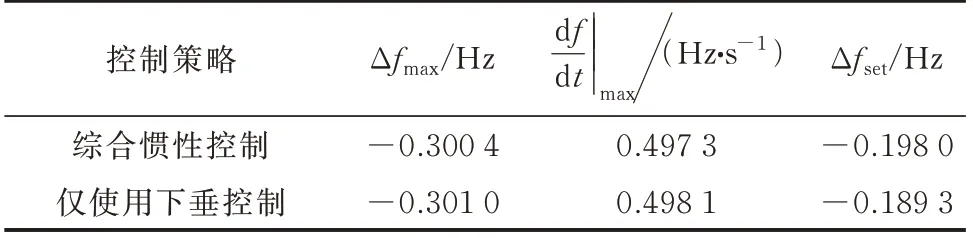
表1 不同风电机组控制策略下的系统频率响应指标对比Table 1 Comparison of system frequency response indices with different control strategies of wind turbine generator

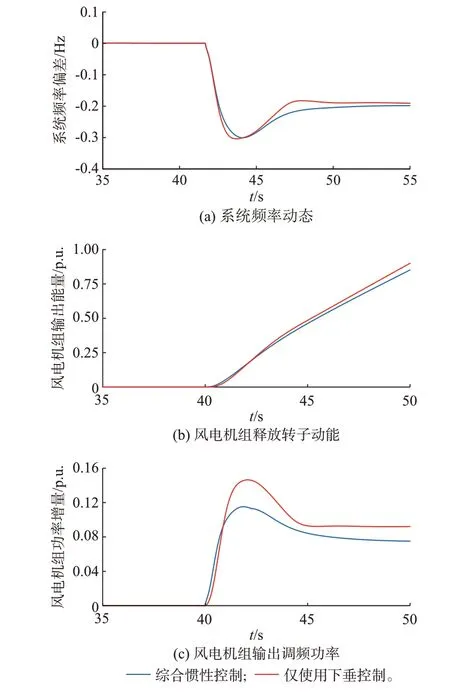
图6 两种控制策略对比Fig.6 Comparison of two control strategies

由图6（a）和表1 可得，基于文中给定的下垂控制系数设定方法，风电机组能在仅使用下垂控制时取得和使用综合惯性控制时相同的频率最低点。同时，系统的稳态频率偏差与下垂控制系数呈负相关，由于风电调频仅使用下垂控制时相较于使用综合惯性控制时增大了下垂控制系数，因而系统稳态频率偏差有所减小，稳态频率有所提高。

风电调频使用综合惯性控制时，同时通过虚拟惯量控制和下垂控制提供功率支撑，而当风电调频仅使用下垂控制时风电机组仅通过下垂控制提供功率支撑。在扰动初期，系统频率变化率较大、系统频率偏差较小，由于虚拟惯量控制输出功率与系统频率变化率成正比，下垂控制输出功率与系统频率偏差成正比，综合惯性控制相较于下垂控制能提供更强的功率支撑。而在系统频率最低点附近，系统频率变化率较小、系统频率偏差较大，由于风电调频仅使用下垂控制时相较于使用综合惯性控制时增大了下垂控制系数，能够提供更强的功率支撑，如图6（b）和（c）所示。

由此可见，基于文中的下垂控制系数设定方法，风电机组能够在仅使用下垂控制时实现替代虚拟惯量控制的目的，并能取得比使用综合惯性控制时更佳的调频效果。