面向多场景辅助服务的大规模电动汽车聚合可调度容量建模

王杨洋，茆美琴，杨 铖，周 堃，杜 燕，Nikos D.HATZIARGYRIOU

（1.教育部光伏系统工程研究中心，合肥工业大学，安徽省 合肥市 230009；2.国网安徽省电力有限公司，安徽省 合肥市 230000；3.国网安徽省电动汽车服务有限公司，安徽省 合肥市 230000；4.雅典国立理工大学，雅典 15780，希腊）

0 引言

在中国“双碳”目标背景下，电动汽车（electric vehicle，EV）得到快速发展。据预测，2030 年全国EV 保有量将近亿辆，储存电能约4 TW·h［1］。EV巨量电能需求的随机性与可再生能源的波动性耦合将加剧电力系统供求时空不匹配性，从而带来电压越限、频率波动等问题［2］。但是，采用EV 与电网互动（以下简称“车网互动”）（vehicle to grid，V2G）技术以及与人工智能技术相结合的现代控制技术，可以将大规模分布式EV 储能聚合成虚拟电厂（virtual power plant，VPP），使其成为电力系统的可调度灵活资源，参与调峰、调频和调压等多层级电力平衡辅助服务，从而实现电力系统整体高效运行［3］。

自然分布的EV 集群（EV fleet，EVF）的聚合可调度容量（aggregation schedulable capacity，ASC）是评估含EV 的VPP 参与特定电力辅助服务能力的重要技术指标。其内涵是指在不影响EV 用户正常使用条件下，EVF 作为能量可以双向流动的特殊负荷与电网进行双向交换能量或功率的上下限［4-5］。

现有研究中，ASC 建模方法主要分为两类:一是针对EVF 整体将自然分布于某一区域的EVF 视为整体进行直接建模的方法［6-8］；二是基于EV 用户个体行为的聚合建模［9-12］。

第1 类方法不关心个体可调度容量（individual schedulable capacity，ISC）。它仅将分属于充电站或配电网内所有的EV 自动视为具有某些相似属性的不同EV 聚合体（EV aggregator，EVA）［6］。这类方法以EVA 整体为对象，假设EV 进入充电站的数量和停留时间均服从一定的概率分布，从而估计充电站不同时刻的EV 数目和电能，进而获得聚合体的ASC。这类方法的模型和参数均建立在经验和假设之上，故泛化能力弱，且忽略了个体控制策略和个体差异性，无法适应充电桩和EV 分布差异很大的省市级规模的ASC 建模场景［7-8］。

第2 类方法由个体EV 的可调度容量模型按照不同的方法聚合成ASC 模型。例如，通常首先根据个体EV 的荷电状态（state of charge，SOC）、充电剩余时间等参数建立每个EV 的ISC 模型，而后对聚合体内所有EV 的ISC 求和得到EVF 的ASC［9］。这类方法主要应用于局部配电网或微网系统中EVF的ASC 建模，因为在微网和低压配电网级别，参与辅助服务的EV 数量少，各个充电站的差异小。

然而随着可再生能源和EV 入网规模的增大，迫切需要EVF 参与地市级配电网与省级输电网协调控制辅助服务。此时，EVF 需要提供兆瓦级的可调范围［13］。这将涵盖大量在地理位置、运行时段、控制策略和额定功率等特性均区别很大的充电桩和EV。因此，省市级大规模EV ASC 的建模问题更为复杂。

现有针对大规模EV 的ASC 建模一般简单将EV 的数量放大［14］，或是假设大量EV 从属于不同参数的概率分布，从而利用蒙特卡洛方法生成ASC 模型［15-16］。此时，通常假设系统内所有EV 从属于一个EVA［14］，或者根据EV 的充电时间等特性设定具体标准分为不同EVA［15-16］。这种聚类方法难以全面考虑影响ASC 模型的多种时空分布因素。因此，难以适用省市级大规模EV ASC 建模。近年来，基于机器学习的自主智能聚类方法在EV ASC 建模中逐渐得到关注。例如，根据EV 的充电时间等特性采用k-means、模糊C 均值［17］或者自组织映射神经网络（self-organizing map，SOM）［18］等方法将相似的EV 或充电桩视为一个聚合体，从而建立配电网或多个充电站大规模EV 的ASC 模型。但现有方法存在受初始值影响较大、容易被异常值影响从而降低聚类效果的问题［19］。而且现有聚类对象一般局限于EV 或者充电桩二者之一，但ASC 模型同时受二者影响。因此，现有聚类方法存在聚类参数考虑不全面的问题。

综上所述，现有大规模EV ASC 模型存在以下问题:1）在大规模EV 数据来源上缺乏真实的大规模EV 充电数据支撑，并且尚未考虑不同辅助服务技术指标对ASC 模型的影响；2）智能聚类方法的应用仅面向EV 个体或者仅面向充电桩进行一次聚类，无法综合考虑EV 和充电桩特性对ASC 的影响；3）聚类算法较为简单，故聚类效果较差，难以应对复杂多维的聚类数据。

针对上述问题，本文面向省市级电力平衡多场景辅助服务，把EV 与充电桩集合定义为EV 广义储能系统（EV generalized energy storage system，EVGESS），以区别于常规储能系统，并提出了一种车-桩信息融合的密度空间聚类（density-based spatial clustering of applications with noise，DBSCAN）和改进的自组织映射（dimension select SOM，DSSOM）聚类组合的双层聚类EV-GESS 聚合体（EV-GESS aggregator，EV-GESSA）ASC 建模方法。本文的创新点如下:

1）本文考虑了调峰、调频和调压的时间尺度和空间参数等技术需求，构建了面向多场景辅助服务的EV-GESS 的ISC 模型以及EV-GESSA 的ASC模型；

2）ASC 模型聚类过程中，结合DBSCAN 和DSSOM 双层聚类算法，从而有效地融合了EV 的时间分布和充电桩的空间分布特性；

3）通过所提出的车-桩信息融合的双层聚类模型和2021 年实际运营数据，获得了某省大规模EVGESS 的ASC 时空特性分布，并对其参与调峰、调频和调压多场景辅助服务的潜能进行了评估；

4）对多种辅助服务场景下的历史ASC 数据的建模和分析，可以成为ASC 多时间尺度时空分布预测的数据基础，进而服务于多场景辅助服务。

1 EV 可调度容量模型

1.1 EV-GESS 的ISC 模型

常规固定电池储能系统的容量由固定的化学电池提供，通过逆变器接口与电网相联系，其额定充放电功率和容量是基本恒定的，其端口输出的SOC 呈现出与充放电功率相关的单调特性，如图1（a）所示。而对于由EV 和充电桩组成的储能系统来说，EV 只有在接入充电桩时才与电力系统发生电能交换。与常规储能系统不同，车-桩系统与电网的接口特性表现为充电桩端口特性，是由充电桩、EV 以及充电策略共同决定的。由于接入EV 的SOC 的随机性，其保有电量也呈现出非单调的波动性质，如图1（b）所示。

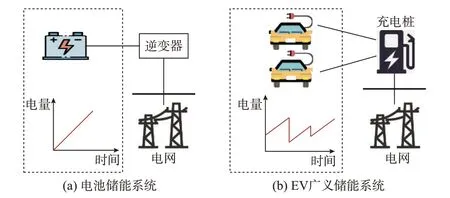
图1 EV 广义储能系统与电池储能系统Fig.1 EV-GESS and battery energy storage system

考虑到现有的EV 充电桩运营数据，大多不记录EV 充电全过程的功率和SOC 变化实时数据。因此，基于EV 实时充电过程数据的个体ISC 建模方法面临缺乏原始数据的困难，因而难以得到应用。但几乎所有的运营充电桩都会记录充电的开始时间、结束时间和充电量等运营记录数据，作为充电的价格结算依据。基于此，本文提出了通过充电桩采集的EV 充电运营记录数据对EV 的ISC 进行建模的方法。

本文采用的建模基础数据为EV 每次充电的充电运营记录，具体包括:本次充电的开始时间、结束时间、本次充电量、初始SOC 和EV 的电池最大容量5 个可变参数，同时还包括充电桩的编号、位置和充电桩额定充电功率和放电功率4 个固有参数。

这些数据不包括EV 编号、车主信息和EV 实时状态等充电过程和行驶过程数据。可以降低车主参与电网辅助服务的隐私泄露疑虑，并间接提升车主的参与率。此外，每次充电过程仅有一条数据，更大大降低了原始数据的传输、记录和存储要求。

基于上述建模基础数据，本文还做出如下假设:

假设1:未调度时每次充电过程EV 均接入即进行充电，完成总充电量后，充电桩即进入停止状态；

假设2:调度过程中，编号为d的EV 的电量不能低于接入时的初始电量Cd，0，而离开时的充电量应当等于初始计划充电量Cd，c。

基于上述数据和假设，本文通过充电过程可行域的边界定量化EV 的ISC，并具体采用可充电容量（schedulable charging capacity，SCC）、可充电功率（schedulable charging power，SCP）、可放电容量（schedulable discharging capacity，SDC）、可放电功率（schedulable discharging power，SDP）4 个指标来描述ISC。

EV 单次充电过程的可行域如图2 所示。

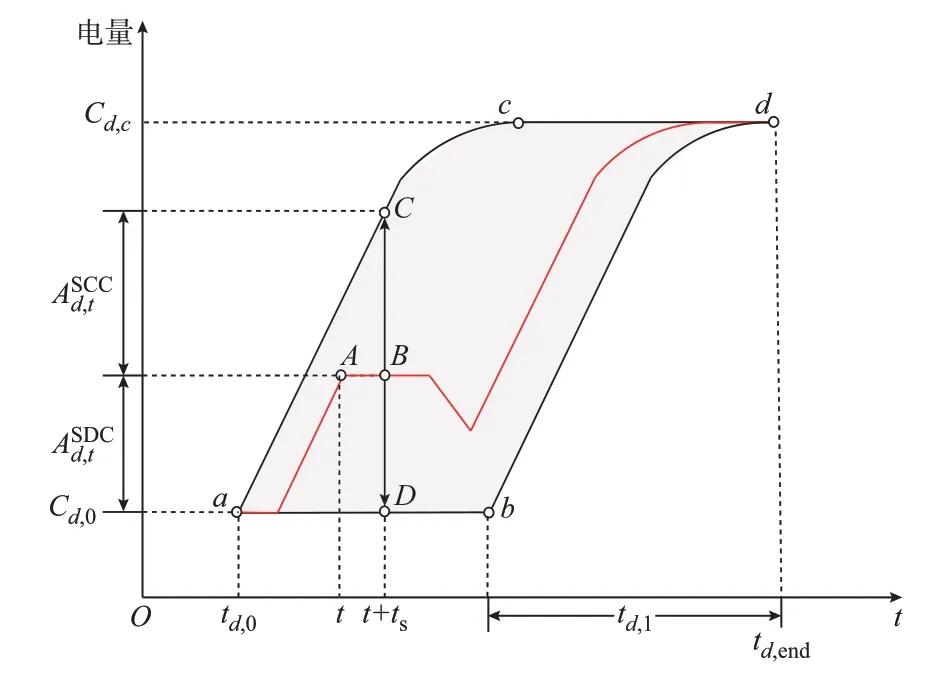
图2 充电过程可行域Fig.2 Feasible domain of charging process

编号d为充电记录编号，EV 在td，0时开始充电，初始电量为Cd，0，在td，end时刻离开。此时其充电过程的可行域为四边形abdc。其中，折线acd为EV 接入时即充电到达成计划充电量而后停止充电直到离开的过程，这是可行域的上限。而折线abd为EV接入时不充电直到距离离开只剩最低充电所需时间td，l的时候才充电的过程，这是可行域的下限。在EV 的调度过程中，必须保证EV 的电量和时间的关系在可行域中，才能满足EV 离开时的电量要求。例如，图中红色折线ad表示的充电过程曲线，t时刻其电量在A点，设响应步长为ts，则在调度时段内［t，t+ts］，其理论上可行域的上下限分别为C点和D点，其SCC（）和SDC（）就是B点离上下限的距离BC和BD。同样地，整个充电过程中，SCC与SDC 的大小均为下一个时刻折线ad沿y轴到线acd和线abd的距离。SCP 和SDP 即为考虑SCC、SDC 以及充电桩充放电限制后的功率上下限。

基于此，对于单次充电过程，SCC/SCP 和SDC/SDP 计算如下:

根据前文假设1，则未调度时Cd，t计算如下:

实际上，充电桩可以大致分为直流快充和交流慢充两种。对直流快充来说，在充电的部分时间可以维持恒定的额定功率，而在SOC 过高或过低的时候充电功率则会降低。交流慢充则可以在整个充电周期内保持充电功率的基本恒定［20］。放电时，两种充电桩均可基本保持恒定放电功率。因此，Pd，c（t）随时间变化，Pd，d不变。本文认为编号为d的充电记录对应充电桩的额定充电功率不大于20 kW时为交流桩，其整个充电过程中充电功率均为额定充电功率。而对于充电功率较大的直流快充，其充电功率先恒定再下降［19］，此时，充电功率Pd，c(t)设计如下:

式中:ks(t)为充电过程中t时刻的估计SOC；为EV 接入时的初始SOC；Cd，max为EV 电池最大容量。

可以看到，在直流快充中，当SOC 大于80%时，其充电功率会不断下降，最终会降低到只有额定功率的一半。

1.2 EV-GESSA 的ASC 模型

EV-GESS 个体通过聚类处理后即形成了EVGESSA。个体EV-GESS 的ISC 模型可以通过其充电记录获得，而EV-GESSA 的ASC 模型则是通过其所属EV-GESS 的ISC 求和得到的。其中，聚类过程将在第2 章详细阐述。本文认为，EVGESSA 的ASC 为所属EV-GESS 的ISC 的闵可夫斯基和，如式（6）和式（7）所示。

式中:Nl是第l个EV-GESSA 的EV-GESS 数目；和分别为第l个EV-GESSA 的原始SCC和SDC；和分别为第l个EV-GESSA 的原始SCP 和SDP。

上述ASC 是在EV 未参与调度时得到的原始值。但调度过程中EV 充放电状态的变化会影响EV 的SOC 等状态，从而影响实际ASC。因此，需要考虑调度计划对ASC 的影响。在调度中，可调度容量变化如式（8）和式（9）所示。

综上所述，不考虑调度的原始ASC 曲线和考虑调度后的实际ASC 曲线的差距是由实际EV 充电功率和调节前的EV 充电功率的差值决定的。如果调度中心仅进行实时调节，在t时刻，由于其过去时间段（0≤τ＜t）调节前后的EV 充电功率已知，其差值是已知的。在此基础上，只要得到了本文提出的可调度容量和功率，即可计算得到当前可用的实际可调度容量和功率。如果调度中心想要制定未来的调度计划，则需要对原始ASC 进行预测，而后滚动修正计算获得调整后的实际ASC 曲线。

1.3 电力系统辅助服务场景对ASC 模型的影响

现有辅助服务市场中，不同场景下对参与调度的集群的时间尺度需求不同。具体来说，应当包括响应时间、响应步长和响应功率的响应持续时间［4，21］。其中，响应时间是指VPP 接到调度指令后，出力达到指令要求时所需的时间。本文假设所有EV 的响应时间是固定的，故不对这一指标进行讨论。

本文选择了响应步长和响应持续时间2 个指标体现时间尺度需求。其中，响应步长ts指可调度容量更新的步长，响应持续时间tl指VPP 响应系统指令后，响应需保持在指令要求的出力状态的时间。

本文重点选取了调峰、调频和调压3 种场景进行讨论。调峰场景下，ts设为15 min，tl设为30 min；而调频调压场景下，ts设为1 min，tl设为3 min［4，21］。可持续时间长度对实际ASC 的影响可以参考附录A 图A1。

不同场景下聚合体可调度容量修正如下:

2 基于车-桩信息融合的双层聚类方法

上文给出了基于个体EV-GESS 的ISC 建模方法以及EV-GESSA 的ASC 建模方法。但是，建立EV-GESSA 的ASC 的前提是已知不同时空分布的EV-GESSA 的分类。本章节将讨论如何通过双层聚类方法将大规模EV-GESS 智能聚合为具有不同时空分布特征的EV-GESSA。

2.1 聚类参数选择

由式（1）和式（2）可以看出，可调度容量的时空分布将受到如下车-桩参数的共同影响。

1）EV 参数（可变参数）:充电接入时间、离开时间、所需充电量、电池额定容量、初始SOC；

2）充电桩参数（固定参数）:额定充电功率、额定放电功率、充电桩经度、充电桩纬度。

其中，充电桩的经纬度决定了EV-GESS 的可调度容量在空间上的分布，而其他参数则决定了其在时间上的分布。

本文主要针对调峰、调频和调压3 种电力平衡辅助服务建立EV-GESS 的ASC 模型。对于调峰和调频来说，充电桩的位置并不是影响辅助服务的决定性因素之一。而对调压来说，充电桩的位置决定了其影响电压的节点，故位置特性影响较大。所以本文提出的聚合模型将根据辅助服务的需求确定是否将位置特性纳入聚类参数中。

由于EV-GESS 的特性是由充电桩的固有特性和接入充电桩的EV 产生的充电记录特性共同决定的，聚类时如果不兼顾EV-GESS 的固定参数和可变参数则难以全面刻画EV-GESS 的真实特性。在大规模EV 应用场景下，仅单个充电桩就可能产生数百到数千条9 维充电记录。因此，总体EV-GESS数据集规模将会迅速增大。而现有的聚类算法，难以处理大规模数据集聚类问题。因此，本文采用了双层聚类模型，其中，一次聚类针对EV-GESS 产生的EV 充电记录数据，聚类参数为EV-GESS 的可变参数，聚类后获得多种充电画像；二次聚类针对EVGESS 本身，将充电桩中各类型充电画像的比例以及EV-GESS 固定参数作为聚类参数，最终形成具有不同特征的EV-GESSA。

本文在一次聚类和二次聚类中分别采用了DBSCAN 和DSSOM 算法。 这是由于虽然DSSOM 算法聚类效果更好，泛化能力也更高，但DSSOM 存在神经网络迭代训练的过程，其聚类速度显著低于DBSCAN，故不适于数据量很大的一次聚类。此外，一次聚类体现为数据量大但数据维度不高，二次聚类体现为数据量较小但数据维度更高，故二次聚类需要降维处理。

本文一次聚类采用DBSCAN，二次聚类采用了深度自编码器和改进的自组织映射（autoencoder-DSSOM，AE-DSSOM）的方法。此外，本文将在算例分析中对不同算法补充的效果进行详细对比分析，从而验证本文算法选择的合理性。

2.2 基于DBSCAN 的一次聚类

2.2.1 一次聚类输入数据

每台EV-GESS 的充电历史记录包含了EV 车主行为习惯信息，一次聚类的目的是根据不同EVGESS 产生的大量充电记录数据，将其聚类为若干类具有不同典型时间和电量特征的聚合体，本文称之为充电画像。充电画像的具体数量则由算法特性和输入数据分布决定。一次聚类过程如图3 所示。

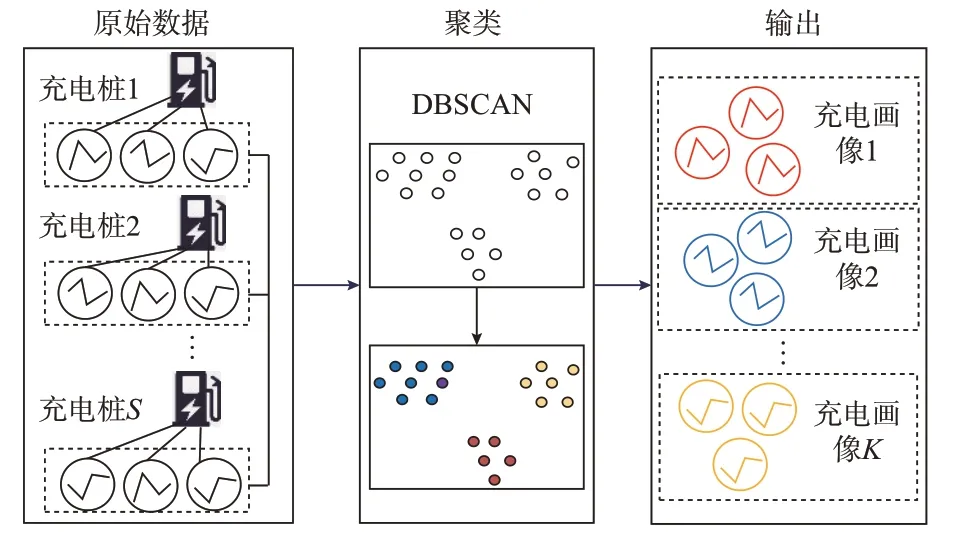
图3 一次聚类过程Fig.3 Process of first clustering

在一次聚类中，所有充电桩下的充电记录作为输入数据，选取的参数有:EV 接入充电桩的充电开始时间、结束时间、充电电量、电池额定容量、初始SOC 和空闲时间比共计6 个参数。其中，前5 个参数可以从充电桩采样数据直接得到，第d个EV 的空闲时间比fd定义如下:

其含义为EV 接入充电桩的总时间中，空闲时间占总充电时间的比例，范围在0～1 之间。越接近1 说明此次充电空闲时间越多，即充电行为具有更高的可转移性，更便于调度。

2.2.2 DBSCAN 聚类算法原理

DBSCAN 聚类算法基本原理与步骤如下:

步骤1:归一化初始数据，设定邻域半径r和最小密度Mmin，将聚类数量l设为1。

步骤2:随机选取一个未被聚类的点O1根据式（12）计算与O1欧氏距离小于r的点的数量M（l），并将这些点和O1聚为一类:

式中:DE(x1，x2)为向量x1和x2的欧氏距离；x1，i和x2，i分别为向量x1和x2的第i个维度元素；I为总维数。

步骤3:如果M（l）≥Mmin进入步骤4，否则进入步骤6。

步骤4:遍历当前类中的其他点，分别计算每个点邻域r中未聚类点的数量，将这些未聚类点包含到当前类中。

步骤5:如果当前类所有点的邻域中未聚类点的数目均小于Mmin，进入步骤6，否则回到步骤4。

步骤6:如果还有未聚类点，回到步骤2，且l=l+1。否则，聚类完成。

DBSCAN 相比常用的k-means 算法具有以下优点［22］。

1）DBSCAN 不需要预先设定产生的聚类个数，降低了先验误差。

2）DBSCAN 对于数据库中样本的顺序不敏感，而k-means 容易被初始点的选取影响聚类结果，故具有更好的聚类稳定性。

3）k-means 聚类后每一类的数量差别不大，这一特性不适用于本文场景。不能假设不同类型的充电记录数量相当，例如，倾向于早上充电的记录相比晚上充电的记录要少很多。

4）少量离群数据对DBSCAN 的影响比k-means小，故DBSCAN 的抗噪声效果更好。

根据充电时间和充电量进行一次聚类所形成的充电画像可以很好地描述充电行为的特征。例如，作为常见的充电行为，夜间慢充很难通过硬性标准合理地规定具体时间和功率以区别于其他充电行为。而通过DBSCAN 聚类算法，可以智能地、非先验地将不同的充电行为区分开，从而可以灵活地适应充电行为数据处理。

2.3 基于AE-DSSOM 的EV-GESS 二次聚类

2.3.1 二次聚类输入数据构成

二次聚类输入数据基于一次聚类的结果以及EV-GESS 的固定参数，其过程如图4 所示。其中，用特征向量描述第s个充电桩的特性。它包括两部分（s=1，2，…，S），一部分是根据一次聚类结果获得的充电画像向量，其作用是描述与此充电桩相连的EV 的行为特性；另一部分为EV-GESS 的固定参数向量，其作用是描述充电桩的固有参数，如充电桩的额定功率，充电桩的空间位置。

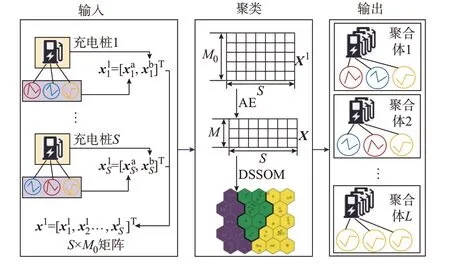
图4 二次聚类过程Fig.4 Process of the second clustering

上述充电画像向量如式（13）所示。

EV-GESS 的固定参数要根据辅助服务场景选取。本文在调压场景中选取经度、纬度、额定充电功率和额定放电功率4 个参数，而在调峰和调频时仅选择额定充电功率和额定放电功率2 个参数。将固定参数向量与充电画像向量合并，从而形成充电桩特征向量，其维度为M0维，在不考虑位置时，M0=K+2，考虑位置时M0=K+4。合计S个充电桩向量形成了充电桩特征矩阵X1作为二次聚类的输入数据。

2.3.2 二次聚类算法

考虑一次聚类结果，并结合EV-GESS 的固定参数，充电桩特征向量有效地描述了EV-GESS 在行为习惯和空间位置上的多种特性。但多维度的输入数据可能会造成聚类速度的下降以及聚类效果的降低。而且大多数维度之间的关系不是完全独立的，存在信息的交叉和冗余。因此，本文选择采用数据降维方法对二次聚类的输入数据进行预处理。

本文采用了AE 降维方法。AE 原理是通过编码器将输入数据压缩成低维度的编码（称为潜在空间），再通过解码器将低纬度的编码解压缩成高维度的数据来重构数据。AE 通过增加多个隐藏层，从而能够对输入数据进行更复杂的非线性变换，从而学习到更抽象的特征表示。其结构如附录A 图A2所示。

通过AE 算法，输入数据实现了降维，从而可以作为DSSOM 的输入数据。DSSOM 是在SOM 的基础上，对各个神经元计算距离、选择获胜神经元以及更新神经元的过程分别进行了改进。其中，SOM算法原理如附录A 算法A1 和图A3 所示。改进DSSOM 算法的核心步骤如下:

1）神经元的距离计算:DSSOM 在神经元与输入数据的距离计算中引入了连接度向量，对神经元j来说，其连接度向量rj=［r1，j，…，ri，j，…，rI，j］。在此基础上，重新计算输入xs与神经元j之间的距离D（xs，wj），计算公式如式（14）所示。

式中:wj为第j个神经元的权重向量；wj，i为wj的第i个参数；ri，j为rj中第i个参数的连接度；I为参数的数量。

可以看到，连接度向量决定了神经元和各个维度之间的权重关系，维度在聚类中的作用越大，则对应的连接度越大。

2）获胜神经元的选择:DSSOM 选择激活度最大的神经元为获胜神经元，激活度形式为:

式中:ac(D(xs，wj)，rj)为神经元j对输入向量xs的激活度；ε为一个大于0 的极小数以防止分母为0。

3）神经元的更新:在DSSOM 中，神经元的权重更新增加了连接度向量rj的更新环节。rj更新前首先要更新距离向量δj，其更新过程如式（16）所示。

式中:β为控制迭代速度的速度参数；e为学习率；Ewin为获胜神经元集合；ew和el分别为获胜和失败神经元的学习率，且0＜el＜ew＜1，这保证了获胜神经元具有更大的学习率，更为保守，而非获胜神经元更倾向于探索不同的新参数。

最后，通过距离向量对连接度向量元素ri，j中的值更新:

不同于SOM，在DSSOM 算法的神经元更新过程中，如果获胜节点的激活度没有达到给定的最小值at，算法不会更新神经元而是创造一个新的神经元，其权重向量等于当前的输入向量xs。然后，将新神经元连接到现有的神经元网络中。可以看到，通过这一设计，使得DSSOM 算法可以根据输入参数的特性智能地改变神经元数目，从而改变最终的聚类数目。

经过上述改造后的DSSOM 算法具体步骤如附录A 算法A2 所示。通过DSSOM 二次聚类，EVGESS 最终被聚类为L个时空分布形态各异的EVGESSA。

3 算例分析

为了验证本文所提建模方法的有效性，本文选择某省级范围4 181 个充电桩在2021 年全年产生的178 万条充电数据作为数据集对本文所提出的方法进行测试。据统计，所选2021 年调查数据涉及充电量约占全省2021 年总EV 充电量的30%。

3.1 个体EV-GESS 的ISC 模型分析

首先，根据1.1 节建立的个体EV 的ISC 模型，对下述某充电记录进行分析:EV 在19:45 接入电网，23:30 离开，共充电15 kW·h，充电桩额定功率为10 kW。基于ISC 模型进行计算，其充电过程中的电量和可调度容量和功率时序分布如图5 所示。

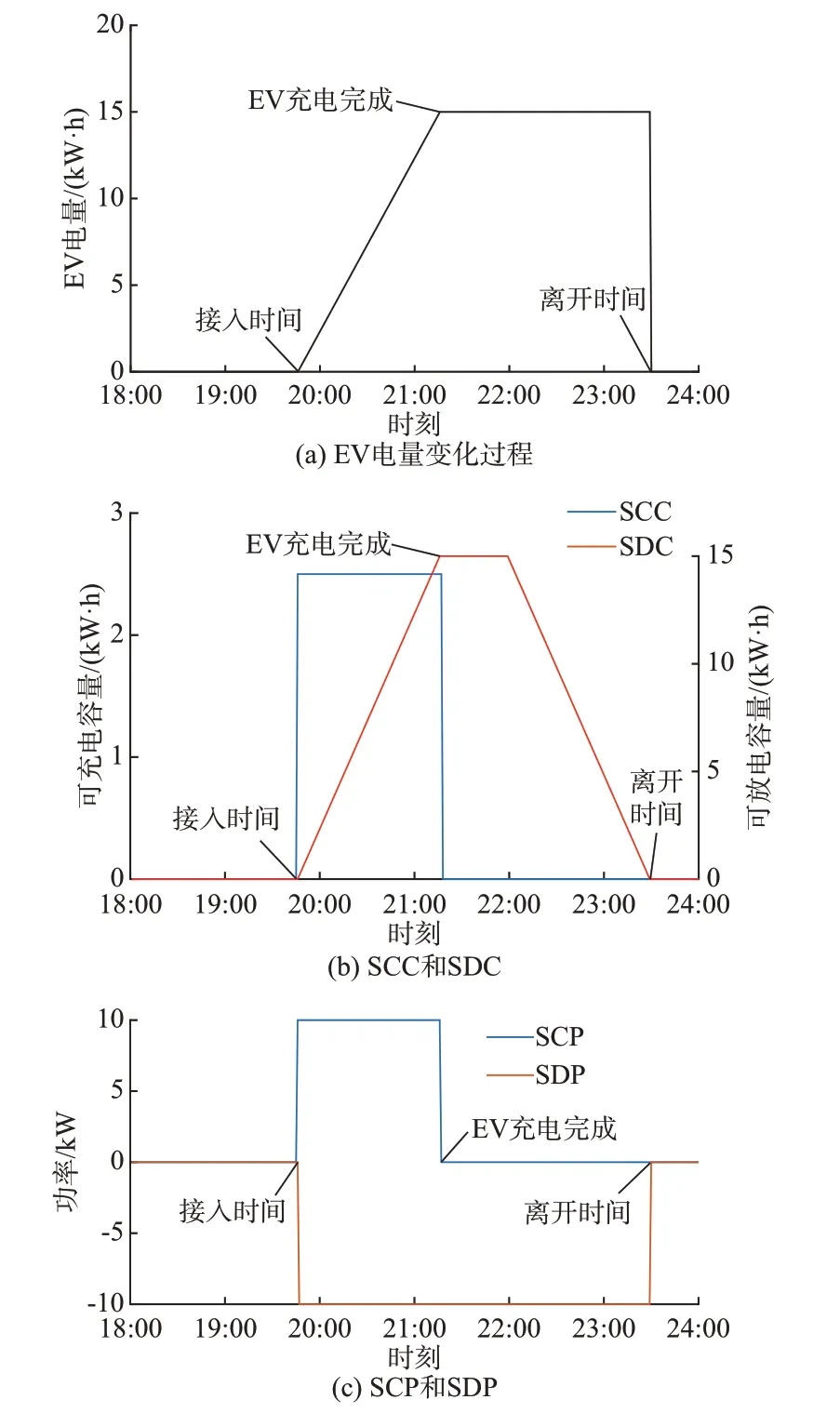
图5 典型EV 充电过程的ISC 曲线Fig.5 ISC curves during typical EV charging process

从图5 可以看到，EV 在19:45 接入电网以最大功率充电直到21:15 充满，而后一直闲置到23:30离开。在其刚接入到充满之前，充电量和SDC 不断上升；直到EV 充电量达到最大，同时SCC 降为0，SDC 达到最大；在该EV 充满到离开过程中，SCC 降为0，SDC 先稳定后下降，直到离开时SDC 降为0。可以看出，本文提出的ISC 模型可以很好地体现EV充电过程中随着电量和停留时间的变化可调度容量和功率随时间的分布。

3.2 一次聚类结果和分析

一次聚类以充电记录数据为输入。其中，对所有充电数据采用式（11）计算得知，全省的fd均值为0.62。一次聚类后，178 万条充电数据被分为8 类充电画像。对每个充电画像所属充电记录的平均充电起始时间、平均充电量和平均fd统计如表1 所示。

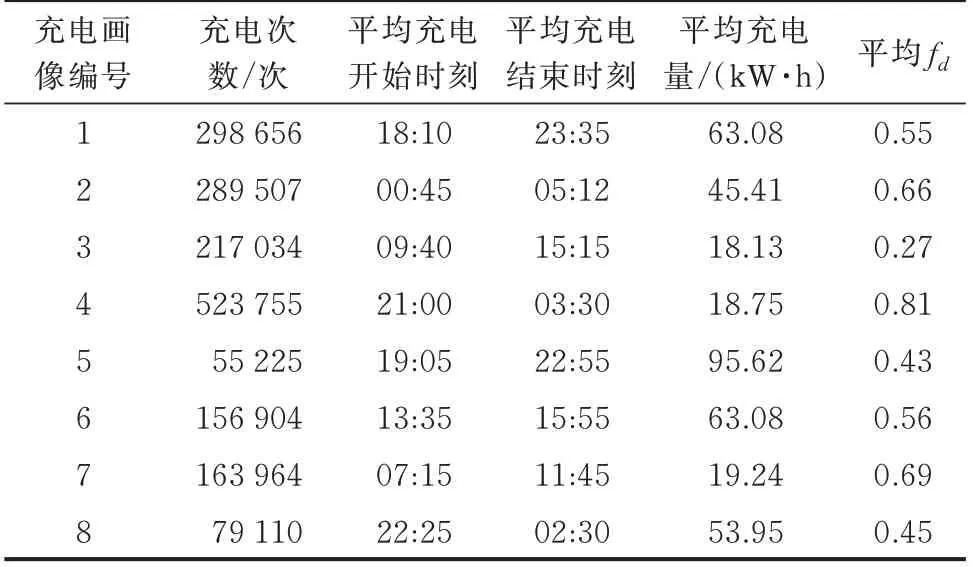
表1 一次聚类结果Table 1 Results of the first clustering

在上述每种充电画像中随机选取200 条充电记录，绘制每条充电记录的充电功率曲线，从而形成8 个充电画像下的充电功率簇，如附录B 图B1 所示。

从表1 和图B1 中可以看到，不同类型的充电画像在充电时间上有明显区别，如分别集中在上午、傍晚、午夜和凌晨的多种充电画像。同时，每一类充电画像有不同的平均空闲时间占比，比如充电画像4，可以视为“午夜型”充电画像，其平均fd为0.81，说明此类充电画像空闲时间很多，便于调度。而充电画像3，可以视为“中午型”，其平均fd为0.27，说明此类充电画像的空闲时间相对较少，不易调度。这说明一次聚类可以有效地得到不同类型的充电画像。而且基于DBSCAN 的一次聚类的充电行为没有规定具体的分类标准，而是智能地根据充电行为的时间和功率特性进行聚类，具有更好地适应性。

3.3 二次聚类分析

在一次聚类结果的基础上，进一步进行二次聚类。二次聚类根据不同场景的辅助服务需求确定聚类参数是否需要位置变量。

3.3.1 不含充电桩位置的二次聚类

在不需要位置变量的场景下，在一次聚类的基础上，对4 181 个充电桩形成充电画像向量，与充电桩额定充电功率相结合，产生10 维向量。

采取AE-DSSOM 聚类，最终将EV-GESS 聚合形成6 类聚合体。每个聚合体内所属的充电桩数目和充电桩的额定充电功率，以及聚合体内充电桩产生的充电记录及其平均fd统计如表2 所示。

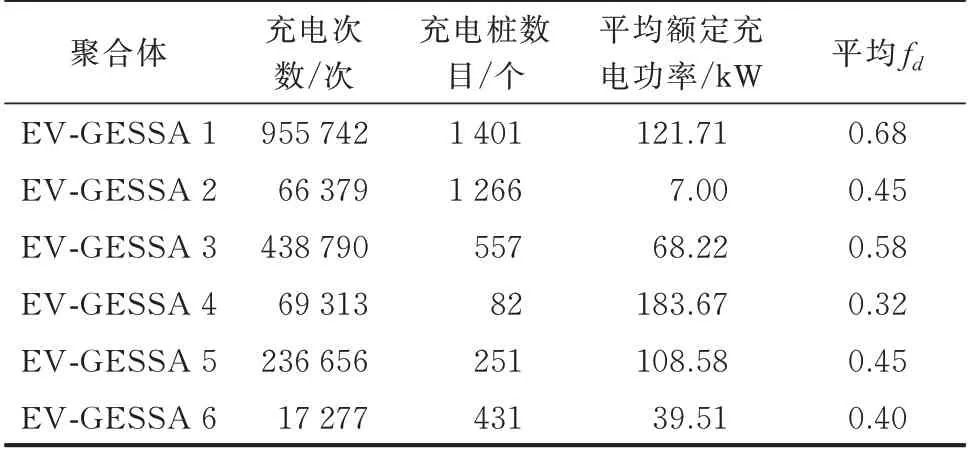
表2 二次聚类结果Table 2 Results of the second clustering

从表2 可以看出，每一类EV-GESSA 有不同的充电时间分布和充电功率。如EV-GESSA 1 以大功率充电为主，EV-GESSA 2 以小功率充电为主，而EV-GESSA 3 以中等功率充电为主。另一方面，不考虑经纬度差别时，充电画像对EV-GESSA 聚类的影响相对变大，不同EV-GESSA 之间的fd差别相对更大。

选取EV-GESSA 1 为例，对可调度容量情况进一步进行分析，结果如附录B 图B2 和B3 所示。图B2 和B3 分别给出了EV-GESSA 1 在调峰和调频2 种场景下的可调度容量和功率曲线。其中，可调度功率即给出了理论上EV-GESSA 1 在调频或者调峰场景下的功率调节上下限。可见，EV-GESSA 1在调峰和调频场景下的可调度容量和功率均呈现出在中午和夜间的双峰特点。但SCC 和SCP 均显著小于SDC 和SDP，这是因为所有EV 都在接入后立即充电。而且，EV 已经以最大功率充电，进一步提升充电容量和功率的空间很小。通过SCC 与SDC的对比可以看到，EV-GESSA 1 在早上09:00 前后SCC 最高，而后迅速降低，但SDC 则降低较慢，且在傍晚达到最低。这说明大量EV 从早上接入电网就迅速充电，直到傍晚才离开。同样地，在20:00 后的夜间时段，SCC 和SDC 均较大，说明EV-GESSA 1在晚间进行充电功率调整的潜力很大。同时，EVGESSA 1 的平均fd为0.68，同样说明了其调度潜力很大。所有EV-GESSA 的可调度ASC 特征统计见附录B 表B1。可以看出，所有的EV-GESSA 都与全局可调度容量分布一样，调峰场景下更长的可持续时间要求降低了SCP/SDP 的范围。

3.3.2 包含充电桩位置的二次聚类

本文的辅助服务调压场景指EV 参与配电网调压，而非全省范围内的输电网调压。因此，选取某省中充电记录最多的A 市作为EV 参与配电网调压的场景。在调压场景下，考虑位置变量，选取一次聚类的结果中属于A 市的数据，对A 市的2 122 个充电桩形成充电画像向量，并与充电桩经度、纬度和额定充电功率相结合，产生12 维向量。

采取AE-DSSOM 聚类，将所有充电桩聚类成6 个EV-GESSA。同样地，对每个聚合体内所属的充电桩数目和额定充电功率，以及聚合体内充电桩产生的充电记录及其平均fd进行统计，并计算了对应的可调资源情况，具体如附录B 表B2 和图B4所示。

从表B2 和图B4 可以看到，不同类型的EVGESSA 包含不同的地理位置和充电功率曲线特性。如EV-GESSA 1 以西北方向的以小功率充电桩为主，而且fd较低，可调潜力较小；EV-GESSA 2 则以中南方向大功率充电桩为主；EV-GESSA 3 在位置上与EV-GESSA 2 相似，但以中小功率充电桩为主，而且其fd更大。类似地，其他EV-GESSA 在地理位置、功率和fd均体现出了不同的特点。

附录B 图B5 以EV-GESSA 1 为例对可调度容量曲线进行详细分析。从图B5 可见，EV-GESSA 1在上午和夜间可调度容量较大。其中，SCC 和SDC在早上10:00 左右后就进入顶峰，说明此时有大量EV 进入开始充电。之后，SCC 在下午约14:30 率先进入最低值，而SDC 在19:00 之后才进入最低值，说明这段时间有很多EV 已经充满电但并未离开，故呈现出一种无法继续充电但可以放电的状态。此外，SCP 和SDP 在中午附近也有很大的上升。其时间特性表明，该EV-GESSA 可以用于中午由于光伏大发造成的配电网电压升高时的调节资源。

3.4 省级规模的EV 灵活资源分析

应用上述所提出的二次聚类模型和聚类结果，可以进一步评估省级范围所有EV-GESSA 的ASC时空分布，从而评估省级规模灵活资源潜力。本文分3 种场景对2 种时间尺度下的EV-GESSA 的ASC 的最大功率和平均功率的可调范围进行对比。3 种场景的数据规模如下:

场景1:采用2021 年调查数据，即4 181 个充电桩产生的178 万条有效充电数据；

场景2:根据2021 年调查数据约占全省总量的30%，推算出2021年全省总充电量规模约为13 936个充电桩产生593 万条有效充电数据；

场景3:以场景2 的数据为基准，按照2030 年EV 保有量约为2021 年的10.3 倍增速［1］，假设车-桩比例保持现有的约3∶1 不变，推算出2030 年的全省约有143 540 个充电桩产生6 107 万条有效充电数据。

不同场景下EV-GESSA 的可调度容量范围如表3 所示。

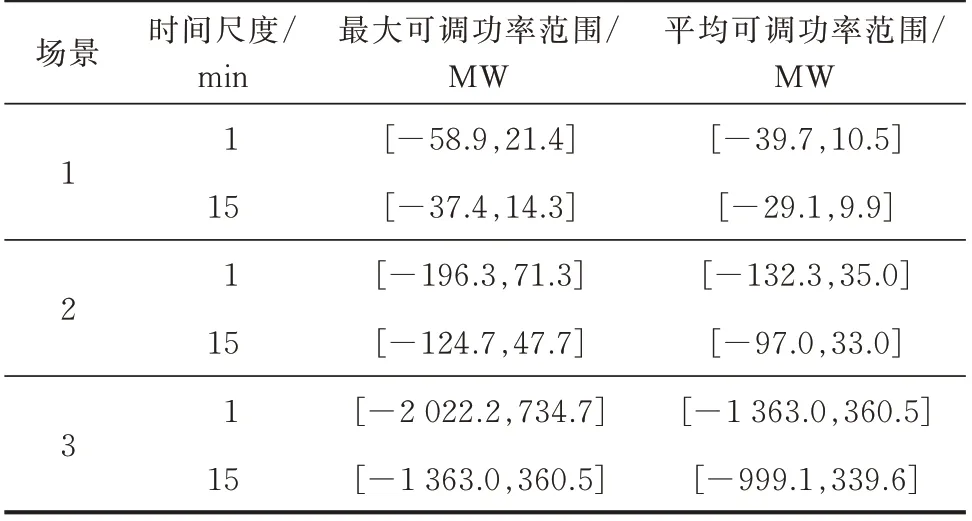
表3 不同场景下的可调度容量范围Table 3 Schedulable capacity ranges in different scenarios

从表3 可以看出，对2021 年调查数据来说，其单日调节能力在不同场景下达到了数十兆瓦级。而根据各地的相关规定，每兆瓦电力平衡辅助服务的补偿约为300～800 元不等［13］［23］。这意味着，仅现有调查数据中的EV 仅与电力平衡辅助服务每小时便有数万元的潜在收益。而到2030 年，全省则有吉瓦级的调节能力，其经济收益将极为可观。

为了评估可调度容量在更长时间尺度上的分布，进一步地对EV-GESSA 1 在单周、单月（12 月）和全年（2021 年）时间长度上的可调度容量和功率情况进行分析。由于SCC/SDC 和SCP/SDP 的波动规律是基本相似的，本文仅选取SCP/SDP 的分布曲线进行展示，结果如图6 所示。

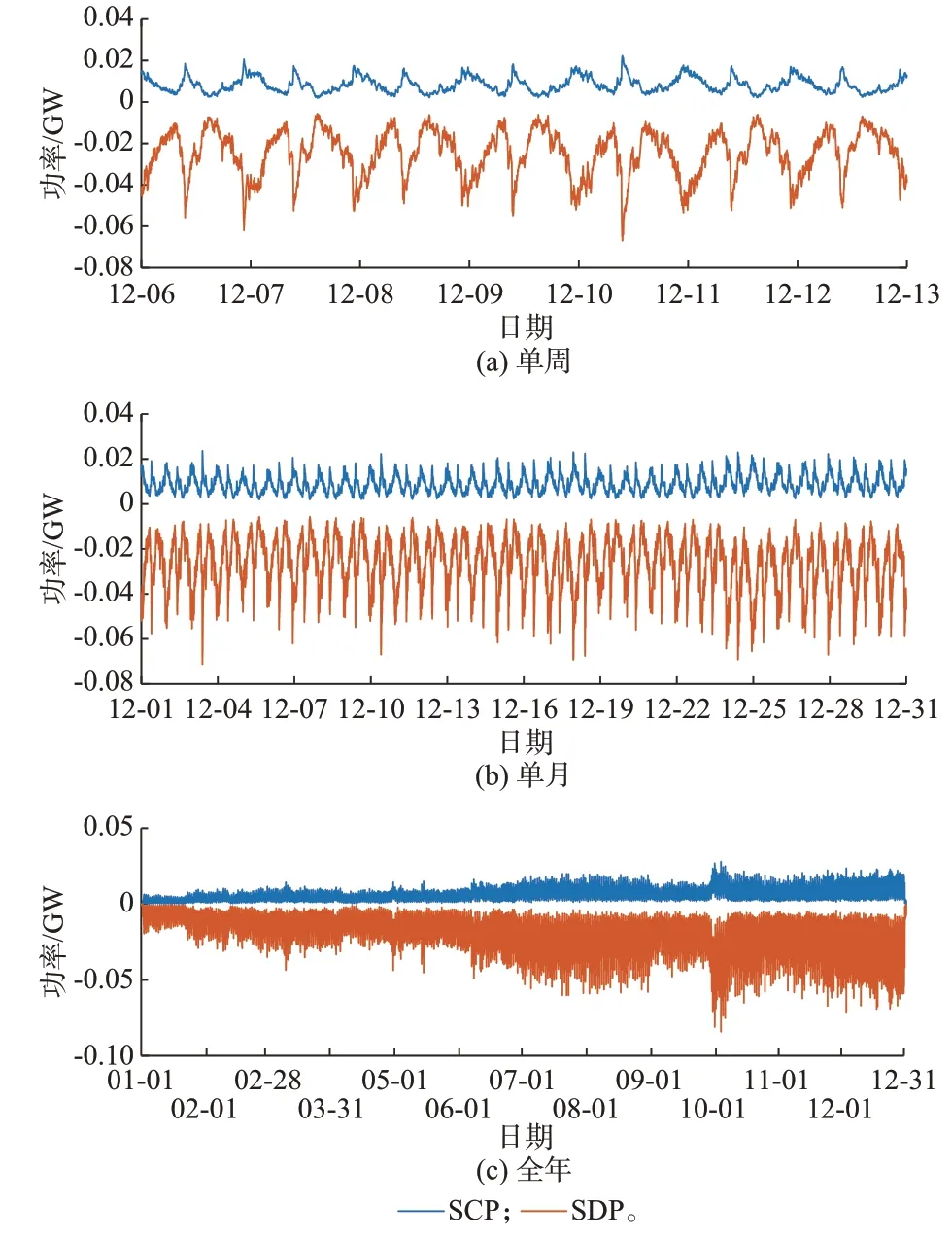
图6 不同时间范围下EV-GESSA 1 的可调度功率分布Fig.6 Schedulable power distribution of EV-GESSA 1 in different time horizons

图6（a）给出了以星期一为开始一周的SCP/SDP 分布。可见，在周末尤其是星期天的时候，SCP/SDP 明显下降，这可能由于非工作日用户充电需求下降造成。而在图6（b）中1个月长度的分布图中同样可以看到的相对低值（如12月5 日、12 月12 日等）。而由全年数据可以进一步看出，一方面2021 年SCP/SDP 有明显的上升趋势，这是由于当前正值新能源汽车大规模发展期，全年有大量新EV 和新充电桩接入电网。另一方面，可以看到“五一”和“十一”等长假对SCP/SDP 的提升效果明显，这和短期周末假期的影响相反。

3.5 聚类算法对比分析

为了验证本文采用的DBSCAN 和DSSOM 聚类算法有效性，本节对包括k-means 和SOM 在内的多种聚类算法在两层聚类的聚类效果和计算时间进行了对比，结果如表4。聚类效果采用Davies-Bouldin 指数（DBI）量化:

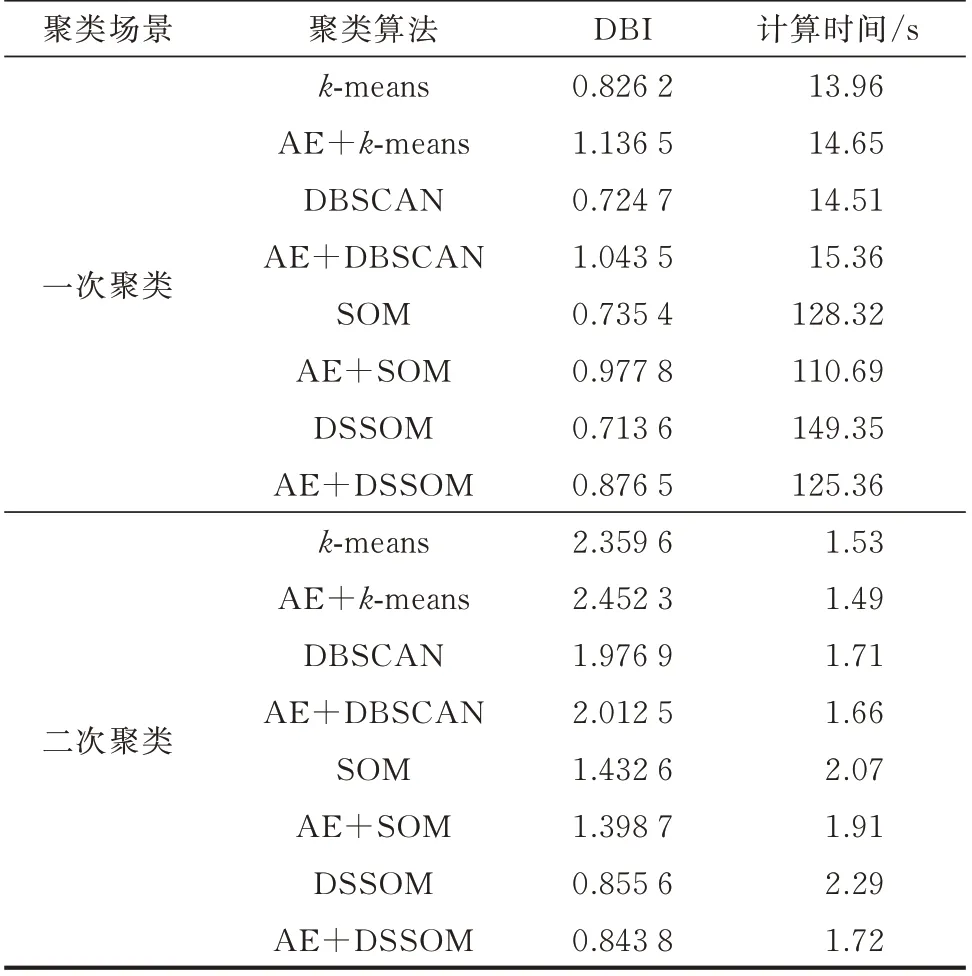
表4 聚类算法对比Table 4 Comparison of clustering algorithms

式中:DBI为DBI 值；G为聚类总数；和分别为第g类和第h类的数据对象与聚类中心的距离均值；dg，h为第h类和第g类聚类中心的距离。DBI 值越小说明聚类效果越好。

本节将基于不同聚类算法的结果分别就一次和二次聚类的算法效果进行分析。

1）一次聚类结果讨论

从表4 可以看出，在不采用AE 时，对比4 种算法可以看到，从聚类效果来看，SOM 和DSSOM 略好于k-means，但与DBSCAN 相当；但从计算时间来看，SOM 和DSSOM 算法的计算时间均达到100 s以上，而DBSCAN 仅需14.51 s。这证明了在数据量巨大的一次聚类中，采用DBSCAN 算法可以获得计算速度和聚类效果的平衡。

在加入AE 进行特征选择下，4 种算法的聚类效果还有所下降。以AE-DBSCAN 为例，AE 环节的引入不仅增加了计算时间，而且DBI 值由0.724 7 增加到1.136 5，上升了56.82%。这说明在数据量庞大但每条数据的维度不高的一次聚类中采用AE 不仅难以实现提高运算速度的目的，而且将会大大降低聚类效果，故一次聚类不适合采用AE 处理。

2）二次聚类结果讨论

从表4 可以看出，在不采用AE 时，对比4 种算法可以看到，由于数据量降低很多，4 种算法的计算时间均较低。而DSSOM 在获得最好的聚类效果（DBI 值为0.855 6）的前提下，其计算时间相对并不长。如相比DBSCAN，DSSOM 在DBI 值降低了56.71%的前提下，计算时间仅增加了0.58 s。总体而言，DSSOM 在二次聚类中可以获得计算速度和聚类效果的平衡。

而在加入AE 进行特征选择后，二次聚类呈现出了与一次聚类不同的效果。一次聚类的数据特性是数据量庞大但每条数据维度不高（6 维），而二次聚类的特性是数据量较小但每条数据维度较高（12 维）。因此，采用AE 进行特性选择降维后，在降低了计算时间的前提下，在SOM 和DSSOM 中还呈现出了提高聚类效果的现象。这是由于通过AE 进行特征选择可以更好地把握高维数据之间的隐含关系，故降低了无关变量对SOM 和DSSOM 算法中神经网络训练的影响，从而产生了更好的聚类效果。因此，对二次聚类来说，AE 特征选择是有效提升聚类速度和效果的手段。

4 结语

针对现有的ASC 模型聚合层级较低，聚合体形成不合理的问题。本文针对大规模EV 参与省市级电网电力平衡辅助服务，提出了基于车-桩信息融合的数据驱动与双层聚类方法。针对不同电力平衡辅助服务场景，分别对ASC 模型的响应步长、可持续时间和空间分布等技术特征进行了分析与评估，基于某省2021 年全年实际EV 充电桩运营数据，采用本方法进行了模拟计算，得出如下结论。

1）本文提出的双层聚类方法，综合考虑EVGESS 的车-桩信息融合，从而可以获得在时间分布、空间分布和fd上形态不同的EV-GESS 的ASC模型。

2）算例分析表明，在省级规模下，2021 年调查数据中的聚合灵活资源，可提供的平均可调功率的上下限在响应步长为1 min 和15 min 时的潜力分别可以达到［-39.7，10.5］MW 和［-29.1，9.9］MW，随着EV 规模的增大，2030 年省级可调功率范围可以达到数吉瓦级。

3）较长时间的可调度容量分析结果表明了在当前形势下ASC 迅速增长的趋势。同时，不同假期影响不同，如周末和春节会降低ASC 而普通法定节假日则会增加ASC。

4）在数据量巨大而数据维度相对不高的一次聚类场景中，采用DBSCAN 算法可以获得计算速度和聚类效果的平衡，而在数据维度相对更高但数据量不大的二次聚类场景中，采用AE+DSSOM 算法相对更好。

5）本文提出的模型可以为大规模EV 参与多场景省市级电力平衡服务ASC 的预测提供基础。由于篇幅的限制，这部分内容将另文讨论。

6）本文仅对现有EV 情况进行了潜力评估，但由于缺乏真实案例数据，未能对真实调度情况下EV 车主的响应情况进行调查分析，故方法有待进一步验证。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。