考虑电力-交通耦合网动态协调的EV集群灵活性挖掘与优化调度

刘志坚，戴 景，杨灵睿

（昆明理工大学电力工程学院，云南省 昆明市 650500）

0 引言

电动汽车（electric vehicle，EV）已成为“碳中和”背景下，提升国家交通领域节能减排竞争力的关键主体［1］。统计资料显示，截至2022 年，中国新能源汽车保有量已达1 310 万辆，呈高速增长态势［2］，规模化EV 的利用在交通系统节能减排方面体现出巨大潜能［3］。随着EV 渗透率不断增长，配电网与交通网之间的联系通过充电站这一中介变得日益紧密［4］。一方面，EV 路径选择与道路拥堵情况相互作用，可能导致充电站利用率不均的问题［5-7］；另一方面，大规模EV 在充电站无序接入配电网，易对配电网的经济安全运行造成冲击［8-10］。但实际上，由于EV 特有的时-空移动灵活性与充-放电储能灵活性，采取有效的调控策略可以为电力-交通耦合网的协调经济运行提供丰富的灵活性资源。

当前，有部分研究致力于发挥EV 的充-放电储能灵活性，且多关注于EV 与电网的交互。文献［11-12］建立了需求响应调控模型，制定EV 的最优充放电计划，实现实时供需平衡，但均将EV 集群的充放电响应能力设定在单一时间断面上，忽视了EV 集群的储能灵活性随调控实时变化这一事实。针对这一问题，文献［13］从EV 集群运营商的角度，提出了EV 集群连续时间断面响应能力模型，并在日内综合考虑单体EV 的响应裕度指标，来实时更新可响应的EV 集群队列，作为参与电网调度的响应边界信息。考虑到对单体EV 按指标分类进行功率调控，大量EV 调度将造成维数灾，文献［14］按比例设定EV 集群的快慢充选择，并采用闵可夫斯基和算法对EV 个体响应能力进行聚合参与主辅市场联合优化。

另一部分研究考虑EV 的时空移动灵活性，对电力-交通耦合网的协调运行进行了研究。文献［15］对考虑城市交通网和配电网相互依赖运行的公共EV 充电站的最优充电定价问题进行建模，但模型只考虑了静态交通流在单一时间片段的分布情况。在动态交通流分配（dynamic traffic assignment，DTA）问题中，常用动态网络加载（dynamic network loading，DNL）模型来描述交通流的动态传播。但是，描述细节交通动力学行为的DNL 模型呈现为高阶运动波模型，过于复杂的DNL 模型集成到耦合模型中时会引入非凸约束集，甚至可能导致对应的DTA 模型的解不存在［16］。关于涉及高阶交通动力学行为的DTA 模型的连续性和收敛性等定性分析在数学上仍在讨论［17］。因此，仅有少数研究针对两网之间的动态互动进行展开。文献［18-19］提出一个弧段、节点权重动态更新的电力-交通耦合网来捕获道路拥堵状况、EV 充电负荷、电价等动态变化情况，但其所提的路段行驶时间通过先验分布进行设定。文献［20］针对路-电耦合网络提出了具有统一性的时空链，以时间格子确定空间位点，每前进一格就实时更新前方路径选择的相关参数。但这些研究均以路径最短原则对EV 个体进行引导，不考虑整个耦合系统的耦合经济运行。而从DTA 的出行选择原则上来说，考虑用户自私的路径选择心理，现有模型较多考虑动态用户均衡（dynamic user equilibrium，DUE）来进行优化［21-24］。

基于以上分析，本文考虑DTA 模型与EV 集群的灵活性调度模型进行集成的实施意义、适用性和可行性，并从电力-交通耦合网的综合效益出发，选择了基于动态系统最优（dynamic system optimization，DSO）理论实现系统最优层面的DTA。首先，构建了基于弧阻抗函数的DNL 模型，描述动态交通流传播情况；然后，对EV 集群的灵活性调度模型进行构建，在兼顾EV 用户特征参数差异性与耦合性的基础上，提出单体EV 灵活运行域数学模型，并采用基于zonotope 线性近似的闵可夫斯基和算法，将各充电站（弧）上的EV 集群聚合成为广义储能。在此基础上，构建双层优化模型，通过对上层交通流最优分配模型与下层配电网灵活性需求响应优化模型之间迭代求解，得到两网当前信息的瞬时单位流量通行成本作为导向，对EV 的出行选择与充放电进行调控。最后，通过与最短路径引导策略在交通流分布、配电网关键节点灵活性供给、电力-交通耦合网综合运行经济效益等方面的比较，验证了本文所提EV 集群调控策略的有效性。

1 基于弧阻抗函数的城市交通流DNL 模型

对于交通网NT(V，A)，其中，V表示节点集合、A表示弧段集合。EV 的路径通常用起讫节点对od来表示，每个路径由节点连接不同路段。为了反映EV 集群在不同弧段、不同节点上形成的异质交通流随时间动态传播的状态，并将其在电力-交通耦合的优化调度中，以简洁的数学形式封装到分析框架中，实现更好的计算效率与模型拓展性，本文提出具有统一性的DNL 模型，对具有时变性、异质性的EV 用户汇聚成的交通流的传播情况进行描述。

1.1 引入虚拟弧段的重构交通网

首先，对交通网进行重构（如图1 所示），使得通行状况不同的节点都能够具有统一的拓扑结构形式（兼具上下游、不在节点滞留），统一看做交叉路口并采用统一的普通交叉路口v∈V的DNL 模型。源节点o∈O⊂V 不具备上游路段，故针对每个源节点o相应引入虚拟节点o′∈O′，以及虚拟弧段o′-o∈Ao；充电站节点r⊂V 受到EV 用户充电排队的影响，存在时滞效应，为统一对路段的时滞效应进行描述，对充电站节点r引入对应的虚拟节点r′∈R′以及充电弧r′-r（标记为弧段c∈C）。则原节点集合扩展为=V∪O′∪R′，弧段集合扩展为=AG∪Ao∪C。其中，O、O′、R′分别表示源节点、虚拟源节点、充电站虚拟节点集合；AG、Ao、C分别表示常规弧、源节点虚拟弧、充电弧的集合。因此，可行路径p∈Pod（Pod表示o-d对之间的可行路径集合）可表示为包含虚弧在内的多条路段的串联形式，如式（1）所示。

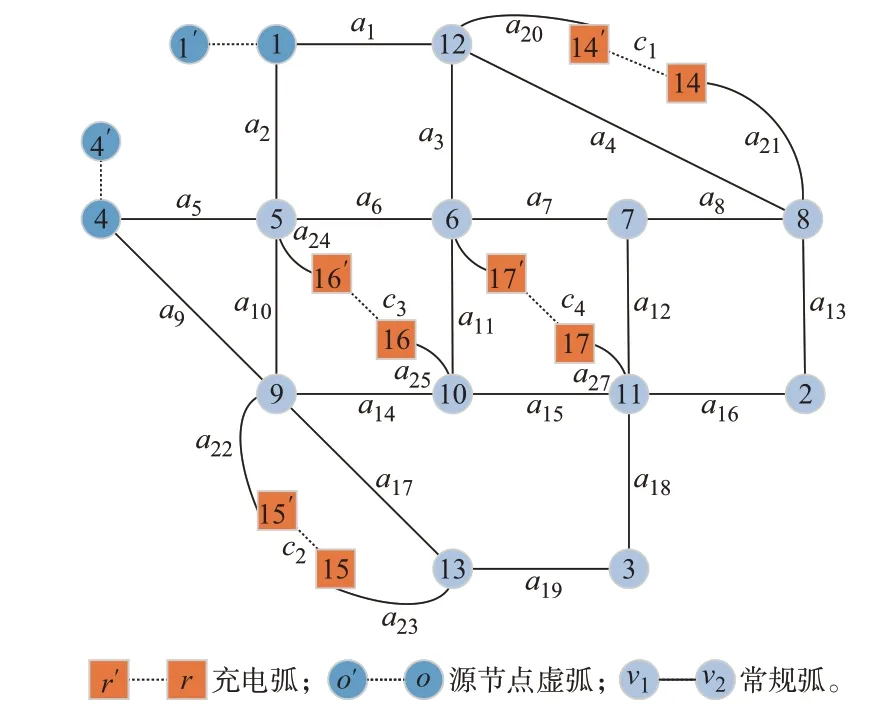
图1 引入虚拟节点及虚拟弧段的重构城市交通网Fig.1 Reconstructed urban transportation network by introducing virtual nodes and virtual arcs

式中:n{p}表示路径p共包含的路段数量；弧段ai，aj∈。

路段承载的交通流会影响各类路段的实时通行时间，进而影响交叉路口上下游路段流量传播的时滞效应。因此，首先参考文献［24］采用瞬时弧阻抗模型来描述各路段对动态流量的阻碍作用。源节点虚弧阻抗τo′-o与常规弧阻抗τa^函数表达式分别如下:

式中:ea^，t为t时刻常规弧a^ 上的瞬时交通流量；ca^为常规弧容量；ta^(0)为常规弧a^ 的零流时间，即无交通流量时一辆EV 自由通行所需的时间；α、β为常数。

由于第m类EV 在充电弧c的弧阻抗函数τc，m需要考虑不同电量特征参数下的EV 充电时间，其兼具时变性与异质性。依据基于排队理论的改进Davidson 弧阻抗函数［25］，将其构建为充电弧c上的瞬时交通流量ec，t的函数，表达式为:

式中:J为影响函数形状的曲率系数；为充电弧c的容量，即站内的充电桩数量；为第m类EV 在充电弧c的基础充电时间；分别为第m类EV 的理想离网电量、最低电量；为第m类EV 的充电效率；为第m类EV 的最大充电功率。

1.2 交通流的DNL 模型

DNL 模型以交叉路口交通流模型作为统一形式，在第3 章将作为模块之一被集成到电力-交通耦合模型中，实现输入时变的路径交通流、输出各路段上瞬时交通流的功能。因此，需先对动态交通流的可行域进行描述:

式中:ea，m，t、分别为t时刻弧段a∈上的第m类EV 对应的瞬时流量、输入流量、输出流量；M 为EV 种类集合；qa为弧段a的通行容量。式（6）描述每条路段上每种类型的EV 汇聚成的瞬时交通流，以及输入、输出交通流之间的耦合关系；式（7）定义了ea，t表示各个路段上的瞬时交通流；式（8）—式（10）表示路段上交通流（瞬时、输入、输出）受路段容量的限制。

1.2.1 交叉路口动态交通流

设流入交叉路口v的路段集合为Iv={a1，a2，…，ai}∈，流出v的路段集合为Ov={κ1，κ2，…，κj}∈(AG∪C)。则交叉路口的流量分配模型可表示为式（11）—式（15）。其中，式（11）定义ρp，a，κ，t为远流向分配比例系数，表示去向为路段κ继而去往路段l的p路径流量占当前路段a进流量的比例，也可以理解为当前经过路段a-κ的交叉路口上的流量若以路径p为引导，将有多少被分配到路段κ-l连接的交叉路口上；式（12）定义ϑa，κ，t为近流向分配比例系数，描述来自路段a去向路段κ的所有路径流量占路段a总流量的比例；式（13）—式（15）用于确定路段a的流出交通流、路段κ的流入交通流、从路段κ去往路段l的p路径流量。

式中:fp，a，κ，m，t、fp，κ，l，m，t分别为t时刻对于p路径而言由路段a到κ、路段κ到l的第m类EV 对应的路径流量；τ*为不同类型弧段的通行时间，响应用瞬时弧阻抗函数（式（2）—式（4））进行计算。

1.2.2 源节点的边界条件

源节点o作为EV 路径的起点，是动态交通网络流量的输入端。为了使所有的弧段都适用1.2.1 节所提出的统一的交叉路口模型，需要对源节点虚弧o′-o引入以下边界条件。其中，式（16）反映了源节点输入的时变流量在源节点o这一特殊节点处的下游分配情况；式（17）反映了出行需求在源节点的输入情况。

式中:fp，o′-o，κ，t为t时刻对于p路径而言由路段o′-o到κ的路径流量为t时刻源节点虚弧o′-o上的输入流量；hp，m，t为t时刻选定了p路径的第m类EV 汇聚成的输入流量；Qod，m，t为t时刻给定的o-d对之间的第m类EV 的出行需求。

2 描述充电站EV 集群响应能力的时变灵活运行域

EV 在充电站接入电网后，可向电网充、放电，在满足自身电量需求的同时，响应电网的灵活性需求。因此，本文采用功率可调节域和电量可调控域对EV 集群的灵活运行域进行描述。但EV 能够为电网提供的时-空移动灵活性与充-放电储能灵活性受出行时空特征参数（起讫点、路径选择、充电站选择、出发时刻、期望在站时长），以及电量特征参数（入网时长、入网电量、期望离网电量、充放电功率、电池容量）等EV 用户参数的影响。因此，首先考虑EV 用户特征参数差异性与耦合性，提出了单体EV的电量灵活运行域，进而考虑单体EV 汇聚成的交通流的时空分布，得到EV 集群参与电网灵活性供给的时变灵活运行域。

2.1 单体EV 的灵活运行域

2.1.1 电量可调控域的关键时间节点

第n辆单体EV 的出行时空特征参数决定了其电量边界在时间轴上的分布以及电量状态的关键拐点。因此，首先对第n辆单体EV 的电量可调控域的关键时间节点进行分析。

如图2 所示，单体EV 的电量可调控域由充电上界和放电下界构成。可以看出，电量可调控域形状由入网时长所决定。随着入网时间增加（离网时刻由tout3n过渡到tout1n，临界离网时刻为tout2n），电量可调控域由abc3fa包围的范围过渡到abc1e1da包围范围，临界状态为abc2da。

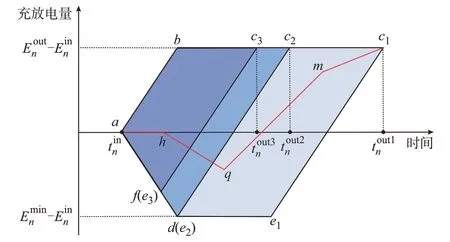
图2 单体EV 的电量可调控域Fig.2 Energy flexible domain of individual EV

考虑EV 里面的排队时间对应于入网时长中的“延迟放电时间”或“延迟充电时间”，假设EV 的入网时长等于充电弧通行时间，则第n辆EV（属于第m类）的入网时长可表示如下:

需保证EV 入网时长不超过期望在站时长Tod，c，m:

2.坚守“守法合规”。尊重国际规则，适应东道国法律要求和业务需要，吸收借鉴国内外先进管理理念、方法和手段，推进管理提升和创新探索，努力打造国际知名品牌，积极建设国际化骨干团队。

可以引入0-1 变量δn，m对EV 短入网、长入网的灵活性供给状态进行标识，则式（21）可用大M法结合式（19）转化为:

因此，充放电边界的关键拐点b、d、e对应的时间节点可表示为:

2.1.2 电量可调控域的电量边界关键拐点

结合单体EV 的电量可调控域模型的关键时间节点与EV 用户电量特征参数，可以对电量边界的动态变化情况进行分析。

入网时间较长的EV 能够完整地完成一次充放电，并可能存在延迟放电时间或延迟充电时间，其充电上界如图2 中折线abc1所示，EV 入网后以最大充电功率充至期望电量后，停止动作直至离开充电弧；其充电下界如ade1c1所示，入网后以最大放电功率放电至最低安全电量后，延迟充电至e1开始以最大功率充电，使离网电量达到期望电量。而入网时间较短的EV，由于不能完整地完成一次全充和全放，其灵活运行域的充放电边界相对更小，在图中表示为abc3fa包围的区域。

因此，第n辆单体EV 的电量可调控域边界可用充电上界、放电下界描述为:

2.1.3 单体EV 的功率可调节域和电量可调控域

电量可调控域所含范围内的任何一条运行线都可表示一种EV 的充放电方式，运行线的斜率即表示单体EV 的充放电功率。以图2 中红线（ahqmc1）为例，ah表示进入充电弧后延迟放电，hq以较低的放电功率放电，qm以较低的充电功率进行充电，mc1以更低的充电功率充电至期望电量后离开充电弧。因此，单体EV 的灵活运行域可用以下单体EV 功率可调节域、电量可调控域表示:

式中:Pn，t为t时刻待聚合的第n辆EV 的功率；η指代前述的有效充/放电率；T为离散时间片段的集合。

可以看出这是一个凸多面体，简写为P(A，b)，具体形式如下:

式中:X∈RN×T为变量矩阵；A∈RS×N为参数矩阵；b∈RS×T为参数向量；T为规划周期内时间片段个数；N为变量个数；S为所有约束个数。

2.2 EV 集群的灵活运行域

EV 通常以集群的形式参与灵活性调控。将EV 聚合成为广义储能可以通过闵可夫斯基和［26］来实现:通过对单体灵活运行域的凸多面体进行顶点对应叠加，以叠加得到的新的顶点集来表示EV 集群的灵活运行域。但随着接入EV 数量增加，凸多面体的维度上升，高维凸多面体的顶点集合获取困难［27］，EV 运行参数的时空耦合性以及差异性导致计算复杂度剧增。因此，提出zonotope［28］来对凸多面体进行线性近似，进而采用闵可夫斯基和算法对EV 集群灵活运行域进行高效聚合。zonotope 通常由一个对称中心u，以及生成向量矩阵H=(hs)，s=1，2，…，S构成:

式中:x为变量向量；αs为生成向量hs方向上的伸缩系数，受αˉ的约束，αˉ为αs的限值。

具体的zonotope 线性近似并聚合得到EV 集群灵活运行域的步骤如下:

步骤1:根据2.1.3 节凸多面体构造生成向量矩阵H；

步骤2:根据凸多面体各平面生成法向量矩阵F=[f1，f2，…，f(S2+S)/2]，计算凸多面体在各个法向量上的延伸距离Δpolytope；

步骤3:根据文献［23］，在凸多面体中寻找最大的内接zonotope，可以用以下优化问题表示:

步骤4:对单体EV 的zonotope 进行闵可夫斯基求和，可以直接通过对称中心、伸缩范围直接叠加得到聚合体的对称中心uagg、聚合体的伸缩范围αˉagg:

因此，EV 集群的灵活运行域可用Zagg(H，uagg，αˉagg)表示，充电弧上的EV 集群能够提供的瞬时灵活性响应能力的可行域为:

式中:Pc，t为t时刻充电弧c上的EV 集群的功率。

3 考虑动态交通流最优分配的EV 集群灵活性调控

3.1 交通网侧动态交通流最优分配模型

DTA 问题的另一个重要构成就是出行选择原则。本文从系统优化运行的层面对EV 出行选择进行指导，并基于DSO 理论对DTA 问题进行最优化模型的构建。DSO 的定义为:假设所有EV 用户均为理性用户，出行者相互配合在各个瞬间选择合理的出行路径使系统的总费用最小［29］。寻求经济出行的单体EV 汇聚成的动态交通流即为动态交通流最优分布。因此，动态交通流最优分布一定满足:任意时刻、任意o-d对之间的路径上一旦有交通流，则该路径对应的一定是最小瞬时单位流量出行成本；只要瞬时单位流量出行成本不是最小，EV 用户就不会选择该路径［30］。这个对路径选择进行指导的瞬时单位流量出行成本可表示为，即瞬时出行成本对当前时刻所使用路径上的出行需求流量hp，t的偏导。

o-d对上的可行路径p的瞬时出行成本由充电成本、通行时间成本以及充电站通行延迟惩罚成本共同构成，可表示为:

式中:λc，t为t时刻充电弧c对应配电网节点的电价；β0、β1分别为常规弧、充电弧的单位通行时间成本。

因此，可将动态交通流最优分布模型用交通网优化（transportation network optimization，TNO）模型表示为:

3.2 充电站对应配电网节点的灵活性需求响应优化模型

在充电站的EV 以集群为整体参与配电网节点的削峰填谷、新能源消纳等灵活性调节服务。因此，从配电网关键节点运行经济性的角度，提出灵活性需求响应优化模型即配电网优化（distribution network optimization，DNO）模型。目标函数考虑最小化分布式电源（distributed generator，DG）发电成本以及弃新能源、弃负荷惩罚费用:

式中:αDG、βDG为DG 对应的发电成本系数；πRE、πLD分别为新能源、非EV 负荷对应的削减成本系数；分别为充电弧c对应的配电网节点的新能源、负荷削减功率；为DG 在充电弧c对应配电网节点发出或吸收的功率。

DNO 问题相应的约束包括EV 集群时变的灵活性裕度描述式（38）、充电站对应的配电网关键节点功率平衡约束式（42）、满足非EV 用户用电需求的负荷功率削减上限约束式（43），以及DG 如燃气轮机的出力上下限式（44）。

为方便后续分析，采用矩阵的形式对DNO 问题进行描述:

式中:pc，t为模型中变量构成的向量；Ac，t、Bc，t、Cc，t、Dc，t为参数矩阵；π为参数向量；λc，t、φc，t分别为等式约束、不等式约束对应的拉格朗日乘子。

3.3 电力-交通耦合下的EV 集群调控策略的双层优化模型

电网与交通网相互耦合的关键点在充电站，而EV 作为电力-交通耦合协同的调控对象，从交通网侧看，EV 用户表现为充电弧流量，从配电网侧看，其表现为接入充电站的具有灵活性响应能力的广义储能。对于EV 用户来说，可以通过当前瞬时单位流量通行成本作为两网运行情况有限的预判，从而对自身的路径选择、接入充电站等做出决策。

因此，实现EV 集群的调控需要考虑电力-交通耦合网的综合效益，可构建交通-配电网优化（transportation-distribution network optimization，TDO）模型如下:

针对T-DO 模型变量之间有着复杂映射和迭代关系的“黑箱函数”问题，可以从电力-交通两侧形成双层迭代优化模型，通过灵活运行域作为边界条件进行传递，充分发挥遗传算法的全局寻优能力进行求解。

具体T-DO 的双层迭代优化模型求解步骤（见附录A）如下:

步骤1:初始化。给定上下层优化问题的收敛系数ε1、ε2。

步骤2:确定本次迭代次数i。初次迭代时，给定各充电弧的初始电价λc，t(i=0)，以及初始充电功率Pc，t(i=0)，并将其赋值给λc，t(i)。

步骤3:上层TNO 模型。根据传入的λc，t(i)对式（40）采用遗传算法（具体计算流程见附录A 图A1）对相应的交通网变量ξTN(i)进行求解，其中，路段交通流与第1 章相对应的DNL 模块生成（具体输入输出见附录A 图A2）。

步骤4:时变灵活运行域计算模块执行（具体见附录A 图A3）。根据交通网侧得到的上层流量分布，得到EV 集群灵活运行域Zagg(H，uagg，αˉagg)。

步骤5:下层DNO 模型。将Zagg(H，uagg，αˉagg)传递到充电站这一层，代入DNO 模型求解得到配电网优化变量ξDN(i)；代入式（47）求解充电站对应配电网节点优化运行的对偶问题DNO-dual，得到沟通引导电力-交通耦合经济运行的充电电价λc，t(i+1)。

步骤6:将得到的λc，t(i+1)传回上层优化模型，重复步骤2 至5，直到上下层同时满足收敛条件。即

4 算例分析

4.1 算例设置

本文根据文献［31］的Nguyen 交通网进行重构，所得重构交通网拓扑结构见图1。作为电力-交通耦合关键节点，充电站设置4 个，为体现各配电网关键节点的灵活性需求差异，分别将c2、c4设定为带风电机组，c3设定为带光伏发电装置，c1无新能源机组。研究时段设为05:00—13:00（长度为5 min 的96 个时间片段），考虑所有EV 的可行路径都包含充电弧，且在该充电弧就能完成充放电，剩余电量足够到达终点，具体的网络路径参数见附录B。此外，EV考虑3 种类型（电动私家车、电动公交车、电动网约车），其出行时空特征参数、电量特征参数等参照文献［14］进行设置，具体见附录B。其余参数设定见表1［32］。本文仿真环境基于MATLAB 平台，上层优化问题采用遗传算法求解，下层优化问题调用Gurobi 9.1.2 求解器进行求解。算例中用于对比的最短路径动态交通流计算也调用DNL 模块。

4.2 算例结果及分析

4.2.1 交通流的最优分布状态

为验证本文所提出的瞬时单位流量出行成本引导下实现的动态交通流最优分布，图3 给出路径p7输入流量及对应的瞬时单位流量出行成本（其他路径见附录C）。

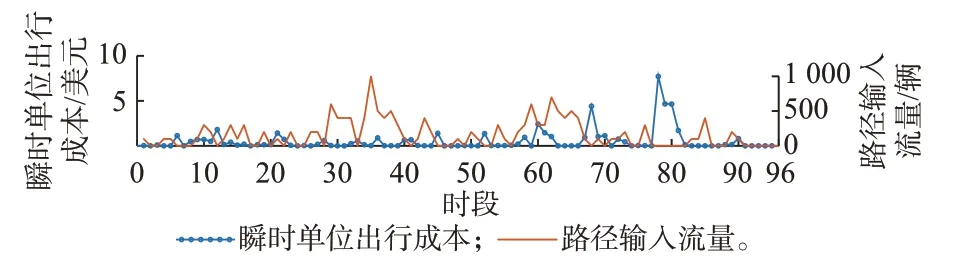
图3 路径7 输入流量及对应的瞬时单位流量出行成本Fig.3 Input traffic flow and corresponding instantaneous travel cost of unit traffic flow of path 7

由图3 可以看出，路径输入流量高峰值往往与瞬时单位流量出行成本曲线贴近底部的值（费用最低点）相对应；一旦瞬时单位流量出行成本升高，EV用户就不会选择该路径，路径输入流量也相应减小。这种与时间相关的路径流量可以看作是不同EV 以随时间波动的瞬时单位流量出行成本为指导做出的自发行为调整所形成的结果。

为进一步研究本文所提出的瞬时单位流量出行成本对EV 出行选择的引导作用，与传统的最短路径引导策略下的交通流分布进行对比，如图4 所示。可以看出，在5 min 为一个单位时间片段的颗粒度设定下，EV 集群调控策略下的交通流在各个路段分布较为均匀，不存在某个路段没有车流的情况，且每个路段的单位时间最大流量不超过35 辆；相反，在最短路径引导策略下，由于含充电弧c1、c2的路径较长，其所涉及路段完全闲置，交通流集中分布于能够到达充电弧c3、c4的路径，导致路径p2-p5所涉及路段的拥堵状况十分集中，且非零交通流路段的单位时间流量在规划周期内全部超过35 辆，最大达到路径容量50 辆。

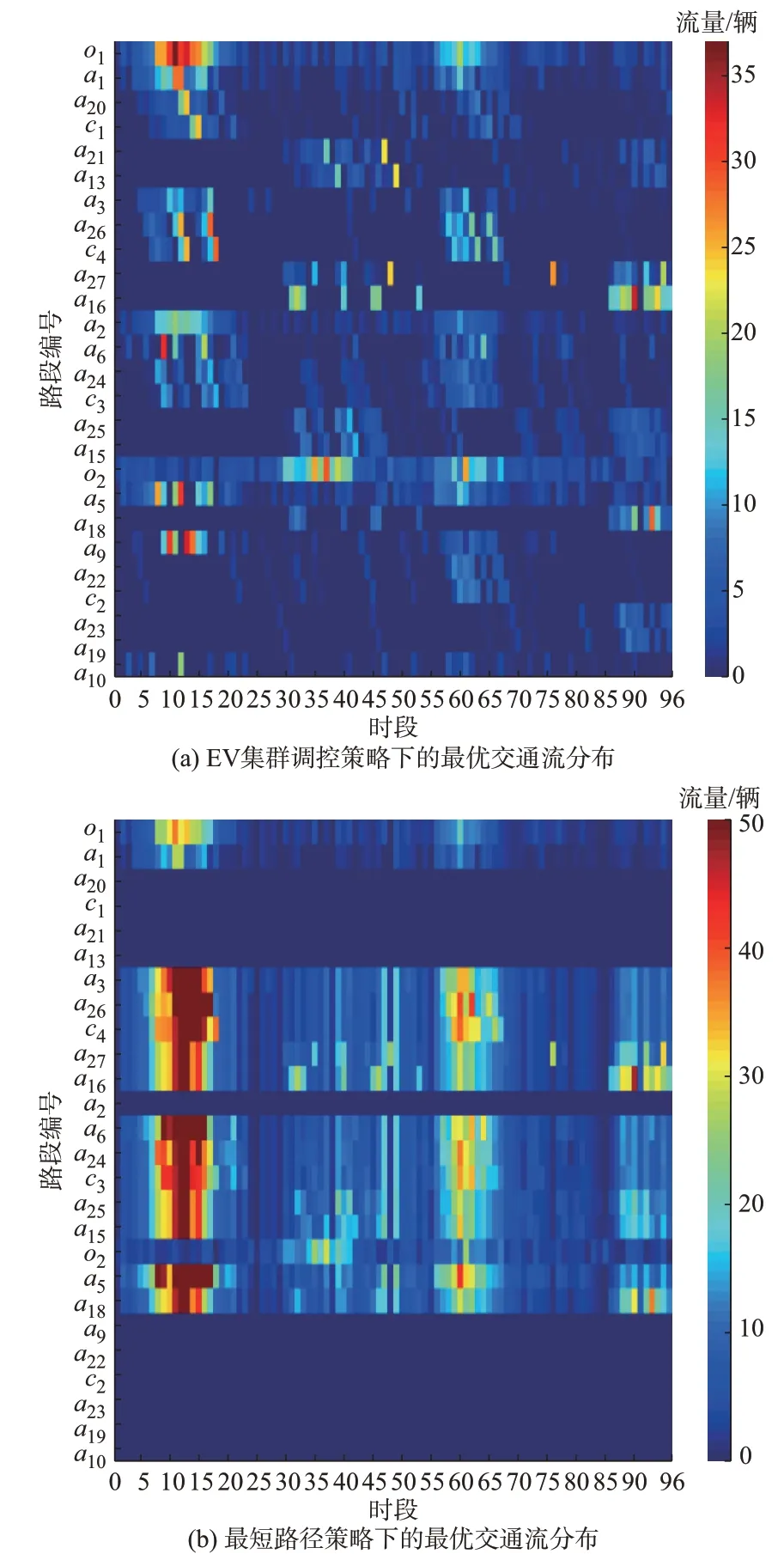
图4 不同引导策略下的交通流分布Fig.4 Traffic flow distribution under different guidance strategies

4.2.2 灵活性响应能力挖掘与EV 集群充放电调控

图5 给出了EV 集群作为广义储能参与充电弧c4对应配电网节点的灵活运行域，其他充电弧的EV集群灵活运行域详见附录D。灵活运行域给出了EV 集群聚合为广义储能并为配电网提供削峰填谷辅助服务的运行边界条件。最短路径策略引导下的EV 集群聚集在c3、c4充电站，导致c1、c2上完全不具备灵活性调节能力，无法满足c1的负荷响应需求，也无法满足c2的多余风电消纳需求；同时，c3、c4上灵活性供给能力与对应配电网节点的多余新能源、负荷的灵活性需求匹配程度不大。

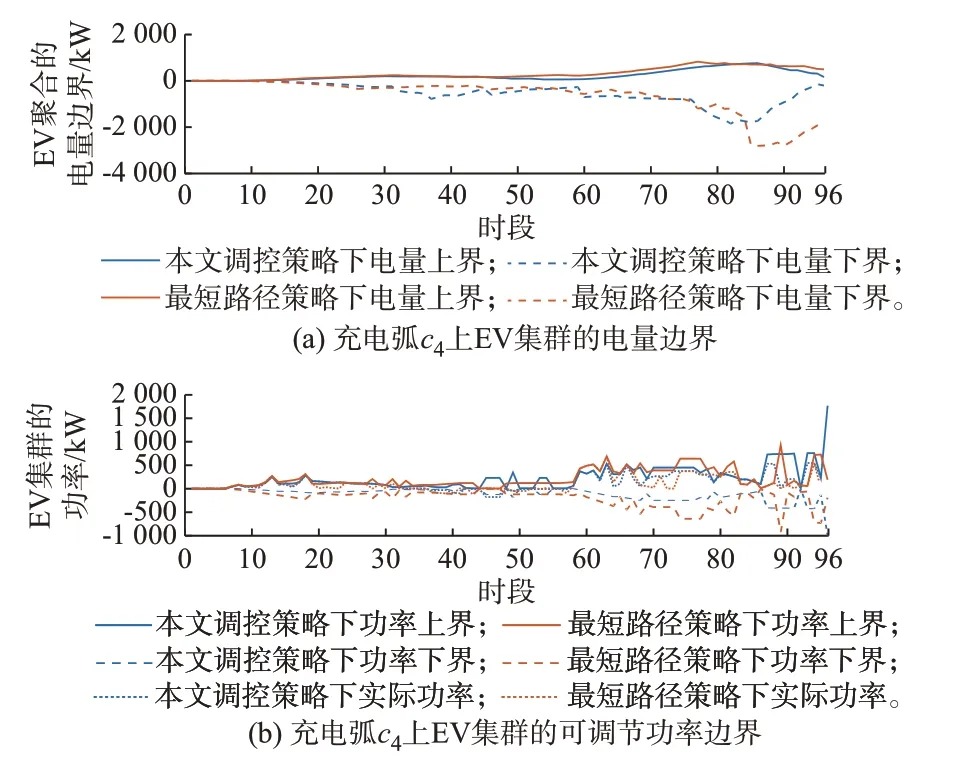
图5 不同引导策略下EV 集群等价的广义储能的灵活运行域Fig.5 Flexible operation domain of equivalent generalized energy storage of EV clusters under different guidance strategies

定义消纳率为EV 集群参与调控消纳的新能源量在无EV 参与调控的原始弃风、弃光量中的占比；定义削峰率为EV 集群参与调控供给的负荷需求在无EV 参与调控的原始弃荷量中的占比。表2、表3分别以消纳率、削峰率两个指标对两种引导策略下EV 集群的灵活性需求响应能力进行衡量。由数据对比可见，EV 集群调控策略引导下的EV 集群相对于最短路径策略多消纳33% 的新能源，多响应25.8%的负荷供应需求。具体两种策略下EV 集群对配电网节点灵活性需求的功率响应细节见附录E。

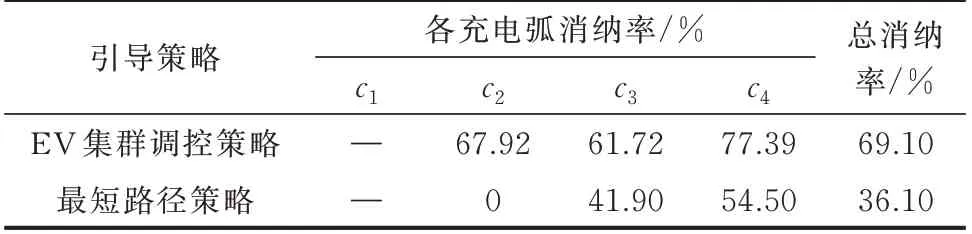
表2 EV 集群的新能源消纳能力Table 2 Renewable energy consumption capacity of EV clusters

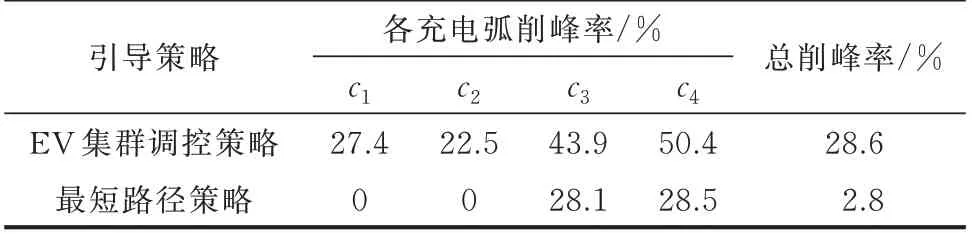
表3 EV 集群的负荷供给能力Table 3 Load supply capacity of EV clusters

4.2.3 经济性比较

进一步，对两种引导策略下的交通侧运行成本及配电网侧运行成本进行比较，如表4 所示。

表4 两种引导策略下的交通网侧和配电网侧经济性比较Table 4 Economic comparison on transportation network side and distribution network side under two guidance strategies

对于交通网侧而言，在最短路径策略下，EV 用户都选择距离自己最近的充电站进行充电，充电站c3、c4的拥堵效应使拥堵费用相对于EV 集群调控策略上涨47.05%。EV 集群调控策略指导EV 用户选择出行更加经济的出行方案，也为交通网动态运行带来了经济分布的流模式。

对于配电网侧而言 ，最短路径策略下c1、c2的灵活性响应效果甚微，配电网优化运行成本高；相反，EV 集群调控策略对EV 的出行选择与充放电进行调控，尽可能挖掘EV 集群的灵活性调节能力，通过接入充电站对相应的配电网节点提供灵活性需求响应服务，减少弃风、弃光、弃负荷，使配电网关键节点实现经济运行。

5 结语

本文考虑EV 作为电力-交通耦合网背景下具有双重属性的跨界主体，构建了动态交通流最优分配下EV 集群灵活性调控的双层模型，以充分发挥EV 特有的时-空移动灵活性与充-放电储能灵活性。通过算例分析，可以得到以下结论:

1）相比于传统的对单一时间片段交通流分布研究，本文提出的基于弧阻抗函数的DTA 模型对路径决策与路段流量时滞效应的内在动态联系进行了深入研究，能够有效描述连续时间片段下交通流的动态传播过程。

2）所提出的单体EV 灵活运行域数学模型能够兼顾EV 用户特征参数差异性与耦合性；同时，引入zonotope 线性近似下的闵可夫斯基和算法，降低了模型聚合的维数与计算量。

3）所提出的考虑中小型电力-交通耦合网综合效益的EV 集群调控策略，在5 min 的时间颗粒度下，耦合模型的求解所需时间大约为2～3 min，所得到的瞬时单位流量出行成本能够同时反映两网当前运行信息，从而指导EV 用户通过调整自身路径选择实现经济出行，实现各弧段交通流、配电网关键节点功率的日内实时经济性调控。

出于耦合模型集成后的计算复杂度以及收敛性方面考虑，本文所提出的DNL 模型忽略了拥堵的波传播特征。为进一步描述真实的交通流动力学行为，采用何种波函数能够方便集成配电网EV 集群灵活性调度模型，这也是后续研究的重点方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。