基于Hammerstein模型的执行机构非线性参数辨识
2024-04-17陈艺文刘鑫屏董子健
陈艺文, 刘鑫屏, 董子健
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
0 引 言
在火电机组中,为了调节执行机构的开度指令与流过其的介质流量能够呈近似线性关系,通常使用阀门流量函数进行控制[1]。然而火电机组的长时间运行会造成阀门内部的磨损,使得执行机构的阀位指令与开度之间原有的对应关系偏离线性关系[2],从而造成火电机组功率非线性控制问题加剧,进而导致火电机组的调频能力下降。当出现上述问题时,运行人员需要对流过执行机构的介质流量进行测量,并采用理论分析和估算得到阀门流量函数的参数,进而对其执行机构非线性特性进行补偿。然而在实际过程中,一些介质流量含有大量粉尘、气液两相流、管道截面积大等问题[3],导致流过执行机构的介质流量难以测量如再热汽温控制系统中的烟气流量,从而无法准确获取并补偿执行机构的非线性特性,甚至严重影响火电机组的安全运行[4]。近年来,大量可再生能源涌入电网,造成新能源的消纳问题日趋严峻,因此对火电机组灵活性改造和提高电网调频调峰能力提出了更高的要求[5]。而火电机组是一个具有非线性特点的复杂系统,其主要原因之一是执行机构具有非线性特性,而执行机构得非线性特性又受到流过其的介质流量难以测量的约束,这个特点使得对火电机组的控制效果很难达到理想水平,因此,为了提高火电机组的控制水平,进而对火电机组进行灵活性改造和提高深调峰能力,必须解决流过执行机构的介质流量难以测量的情况下,执行机构的非线性特性求取问题。
目前获取流过执行机构的介质流量的方法分为直接测量法和间接测量法。文献[6]运用直接测量法的思想设计开发了一种棒状静电传感器速度测量系统,对电站锅炉进行了现场测试。通过实际应用和分析发现,传感器经常发生故障并且容易老化,使得电厂运行和维修成本增加,而间接测量法可以有效的免这一问题,因此越来越多的研究人员开始使用间接测量法代替直接测量法。如文献[7]采用数据和机理相混合的分析法建立了烟气流量的预测模型,并使用数值拟合方法得到模型各项参数。但建立这些模型需要大量的参数,并且当模型太过复杂时,人们就无法精准的预测模型,因此测量流过执行机构的介质流量问题是一个难点。为了进一步研究非线性特性的求取问题,研究人员开始采用特定的模型并求取模型参数来表示非线性系统。如文献[8]使用了类Hammerstein模型的建模方法建立了压电驱动器迟滞模型,并利用参数重组和最小二乘法相结合的方法辨识出压电驱动器迟滞模型的参数。文献[9]提出一种基于Hammerstein模型的电子节气门系统建模方法,并成功辨识出了电子节气门中的线性和非线性子系统。文献[10]通过建立Hammerstein模型,并结合粒子群算法,成功辨识出微燃机-冷热电联供机组的动态特性。上述文献表明可以通过建立Hammerstein模型解决非线性系统的参数求取问题,因此可以将其领域扩展到执行机构的非线性系统参数辨识上,但是在上述文献中使用的算法对Hammerstein模型的辨识精度不高。于是文献[11]针对一类智能算法辨识精度不高的问题,对樽海鞘群算法中的追随者位置更新进行改进,实验结果表明,该算法能够稳定且准确的对永磁电动机的参数进行辨识,但是并没有解决樽海鞘群算法前期收敛速度较慢的问题。文献[12]针对樽海鞘群算法收敛速度慢的问题,提出了一种樽海鞘群与粒子群优化算法结合的特征选择方法,实验结果表明,所提出的算法能够迅速且准确的获得全局最优解。
针对上述问题,本文提出用构建Hammerstein模型代替直接测量介质流量的间接测量法,进而求取执行机构的非线性特性,然后使用粒子群-樽海鞘群混合算法(IPS)求取了Hammerstein模型的各项参数,并与粒子群算法和樽海鞘群算法求取结果相比较,最后基于烟道挡板的开度指令数据和再热器出口温度数据进行了仿真验证。
1 非线性特性模型分析
1.1 Hammerstein模型
非线性系统因其复杂性,一直以来都无法用一个特定的模型来表示。目前被提出并广泛用于表示非线性系统的有volterra级数、块状结构非线性模型等,相较于其他的块状结构模型,Hammerstein模型现已拥有非常丰厚的理论研究基础,在此之上,可以将其领域扩展到执行机构的非线性辨识上[13]。
Hammerstein模型由一个非线性环节后置一个线性环节构成,该非线性模型因其容易构建,且可被灵活使用等优点而被诸多领域采用[14],例如化工过程、换热过程、控制、信号处理及生物医药等。也因此,该模型的系统辨识在目前的块结构非线性模型系统辨识中是聚焦了颇多的研究者的目光[15]。Hammerstein模型图如图1所示。

图1 Hammerstein 模型图Fig.1 Hammerstein model diagram
其差分方程表示为
A(z-1)y(k)=B(z-1)x(k)+C(z-1)ξ(k)
(1)
(2)
(3)
(4)
(5)
式中:u(k)和y(k)分别为可测量的系统输入和系统输出;x(k)为不可测量的无记忆非线性增益环节的输出;ξ(k)为高斯白噪声序列,其均值为0、方差为σ2,ξ(k)和u(k)不相关。z-1为时间序列算子,也叫滞后算子;A(z-1)、B(z-1)、C(z-1)是滞后多项式。此时,辨识Hammerstein模型各项参数的问题就是在一个适应度函数的评价下,求取一组合适的非线性增益参数{ri}和线性子系统参数{aj}、{bj}、{cj},使适应度函数的值最小[16]。
1.2 执行机构与被控对象分析
本文以锅炉中的再热器为研究对象,进而研究执行机构的非线性特性的参数求取问题。
为使再热汽温能保持在规定的安全范围内,通常以烟气侧挡板开度加以控制,如图2所示。其主要原理是在再热汽温控制过程中,将烟气挡板装配在烟道中,通过调整过热侧、再热侧烟气挡板的开度来改变烟气在两个平行烟道中的释放量,然后对错列布置在两个平行烟道内的低温再热器和低温过热器进行调温,进而使得再热汽温保持在所需的安全范围内[17]。
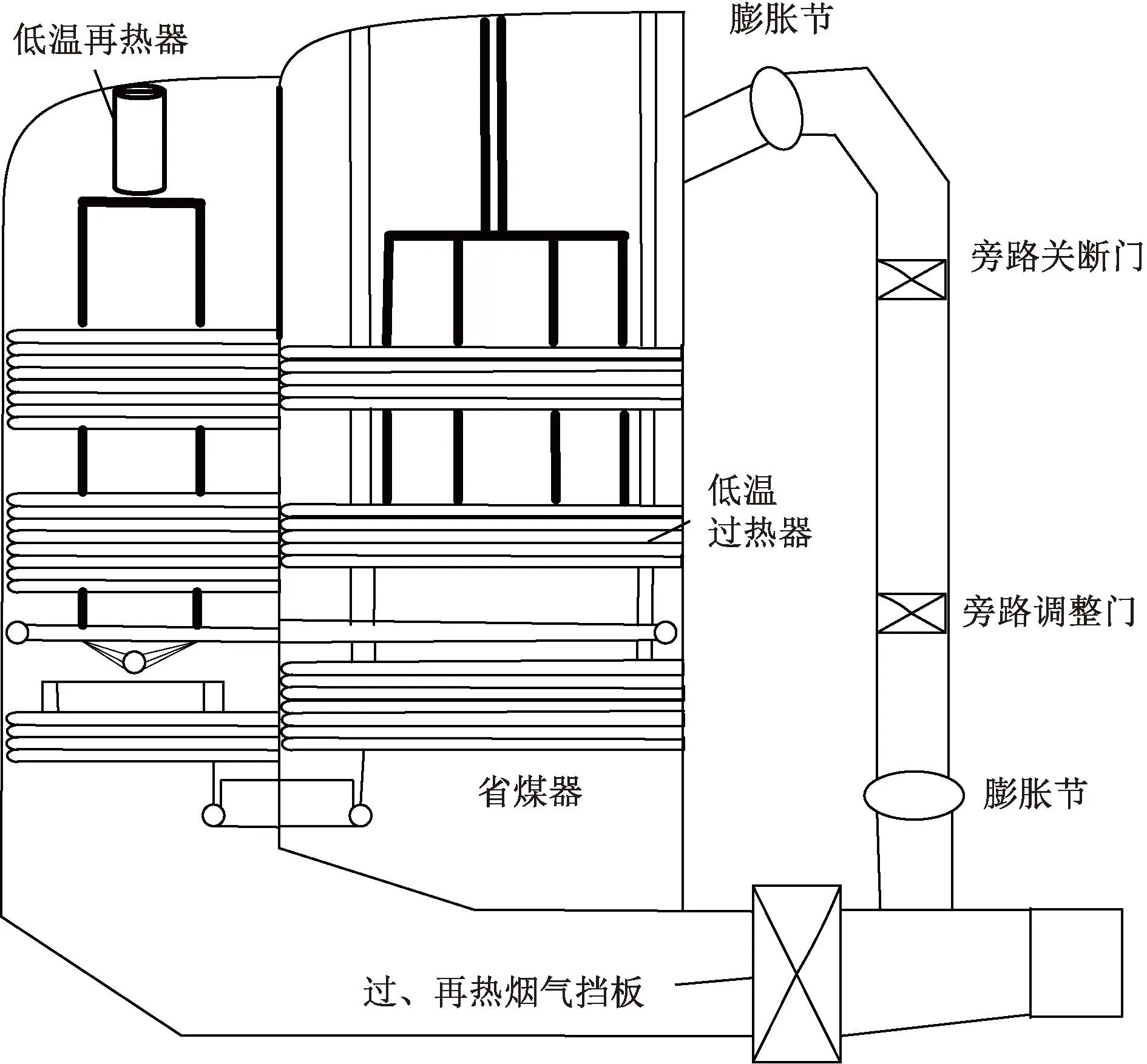
图2 烟道挡板结构图Fig.2 Structural drawing of flue baffle
在实际过程中,烟气流速w可以近似表示为
(6)
烟气流量Q为
Q=wF
(7)
式中:w0烟道入口流速,T0为烟道入口温度,F为烟气流通面积。
烟气温度T与再热汽温T1的关系为
T=kT1
(8)
因此烟气流量Q和再热汽温T1的关系为
(9)
令
(10)
则
Q=KT1
(11)
式中:k,K均为比例系数。
式(11)表明再热汽温与烟气流量呈线性关系,即被控对象是线性的。然而,发电机组经过长期运行或在检修之后,烟道挡板内部结构的磨损会导致流过其的烟气流量与开度之间存在非线性关系,即执行机构是非线性的。因此可以用Hammerstein模型中的非线性子系统和线性子系统分别表示烟道挡板和再热器,从而构建出烟道挡板-再热器Hammerstein模型,其模型图如图3所示。此时辨识出Hammerstein模型的各项参数就可求取烟道挡板的非线性特性。

图3 烟道挡板-再热器模型图Fig.3 Model diagram of flue baffle reheater
2 基于IPS的非线性特性模型的辨识方法
2.1 适应度函数
适应度函数是评价群体质量的重要基础之一。对适应度函数的选择,是种群中个体位置变化与更新的重要基础之一,它对算法的收敛性和快速性具有很大的作用,是评估精度高低的重要指标。
基于最小二乘法的思想,将实际模型的输出与参数模型的输出之间的差的平方和作为系统辨识模型的适应度函数[18]。即
(12)
式中:J为算法的适应度函数;y为被控对象即再热器出口温度的实际测量值;y(k)为被控对象的辨识参数值。此时要辨识的非线性系统问题就转化为适应度函数上的极小化问题,然后使用粒子群算法和樽海鞘群算法求解这个极小化问题,进而得到烟道挡板-再热器Hammerstein模型的各项参数值。
2.2 粒子群算法
粒子群优化算法[19](Particle Swarm optimization,PSO)的原理是在一个M×D维的搜索空间,M为粒子数量,D为空间维数,粒子位置矢量和速度矢量分别表示为xi=(xi1,xi2,…,xiD),i=1,2,…M,vi=(vi1,vi2,…,viD),i=1,2,…M,然后利用适应度函数对所有粒子的当前位置做出评估,并从中找到最好的位置即个体极值,而全局最好的位置为全局极值。其中令粒子个体极值pbest=(pi1,pi2,…,piD),粒子全局极值为gbest=(pg1,pg2,…,pgD)。通过这两个极值,其余粒子开始进行迭代更新。对于第j次迭代,PSO中的每一个粒子按照更新公式(13)、(14)变化粒子的两种属性:
(13)
(14)
式中:vidj和xidj分别为粒子i在第j次迭代的第d维分量的速度和位置矢量;pid为粒子i在第d维分量的个体极值pbest;pgd为第d维分量的群体全局极值gbest;w为惯性权重;q1、q2为学习因子;m1、m2为[0,1]范围内的随机数。
PSO算法相对于其他的寻优算法,需要调整的参数较少,实现较为简单且搜索速度较快,但是PSO算法在算法后期,种群容易受到局部最优解的欺骗,出现“早熟”收敛现象[20],从而使得算法寻优精度较低。
2.3 樽海鞘群算法
樽海鞘群算法[21](Salp Swarm Algorithm,SSA)是一种群智能优化算法,广泛用于解决多种优化问题。该算法最初是受到樽海鞘生物的群居方式的启发,通过观察樽海鞘捕食的链式的群行为而建立的数学模型,这个链式的群行为又叫樽海鞘链。
具体原理是假设在一个D×N的搜索空间,N为种群数量,D为空间维数。种群初始化公式是按照式(15)进行变化的:
XD×N=rand(D,N)×(ub(D,N)-
lb(D,N))+lb(D,N)
(15)
式中:rand(D,N)为D×N矩阵,其矩阵内部值为[0,1]的随机数,ub和lb分别为搜索空间的上界和下界,也就是搜索的范围。
SSA采用式(16)更新领导者位置:
(16)
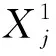
式(16)表明食物的位置决定着领导者的位置更新。q1是SSA算法中的重要参数,它随着迭代数变化而自适应调整,q1的取值公式如式(17)所示:
(17)
式中:l是目前的迭代次数;Lmax是SSA算法中种群的最大迭代次数;q1是一个2→0的递减函数。
樽海鞘链移动时,它的运动符合牛顿运动规律。根据这一规律,其追随者的位置公式如式(18)所示:
(18)
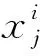
(19)

2.4 粒子群-樽海鞘群混合算法
受到文献[12]的启发,本文将SSA算法和PSO算法结合在一起,先利用PSO算法生成初始化种群,在混合算法前期时,通过利用PSO算法的更新机制对种群位置进行更新,来解决SSA算法前期收敛速度慢的问题。达到混合算法中期时,由于PSO算法在参数寻优过程中容易陷入局部最优,所以利用SSA算法的更新机制对种群位置进行更新,来解决PSO算法后期陷入局部最优的问题。粒子群-樽海鞘群混合(improved PSO-SSA,IPS)算法的具体流程如图4所示。
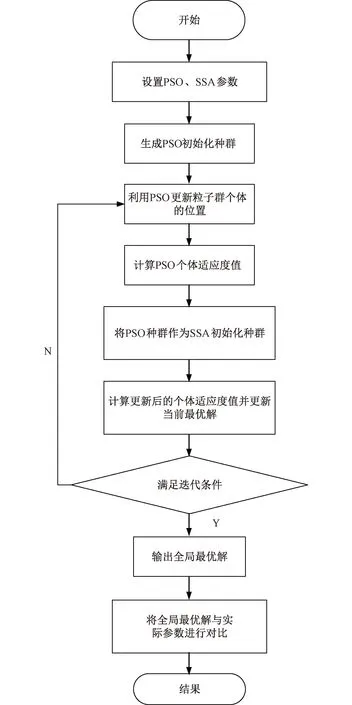
图4 IPS算法辨识流程Fig.4 IPS algorithm identification process
其具体步骤如下:
步骤1:初始化粒子群和樽海鞘群算法参数,包括PSO算法的速度范围,粒子范围,种群大小,学习因子等参数以及SSA算法的搜索上下界。生成PSO算法的初始化种群。
步骤2:计算PSO算法每个解的适合度函数,通过适应度函数的大小来确定最佳解。
步骤3:将PSO算法迭代后的种群位置、最佳的群体极值以及最佳的适应度值分别作为SSA算法的初始种群位置,食物位置,最佳适应度值。
步骤4:利用SSA算法中的领导者更新公式对初始种群位置进行迭代更新,并计算适应度函数的值。
步骤5:判断适应度函数的值是否逐渐减小,若不满足此条件,则返回步骤2,直至满足迭代条件,满足迭代条件时,输出全局最优解。
步骤6:将算法输出的全局最优解与要辨识的非线性模型的实际参数进行对比,计算误差。
3 非线性特性求取结果与分析
利用Matlab/Simulink软件建立再热汽温模型,以660 MW超超临界燃煤锅炉为例,其再热器出口温度维持在630 ℃左右。将烟道挡板指令作为输入,干扰选用均值为0,方差为0.01的高斯白噪声,选择三阶多项式作为再热器的执行机构模型,选择烟气流量与再热器之间的等效传递函数作为被控对象,从而构建出再热汽温模型,如图5所示,其中Constant为常量模块,Product为乘法模块,Add为加法模块。针对烟道挡板-再热器Hammerstein模型4个线性子系统参数和3个非线性增益参数辨识问题,利用PSO,SSA,IPS等3种算法进行了仿真研究。
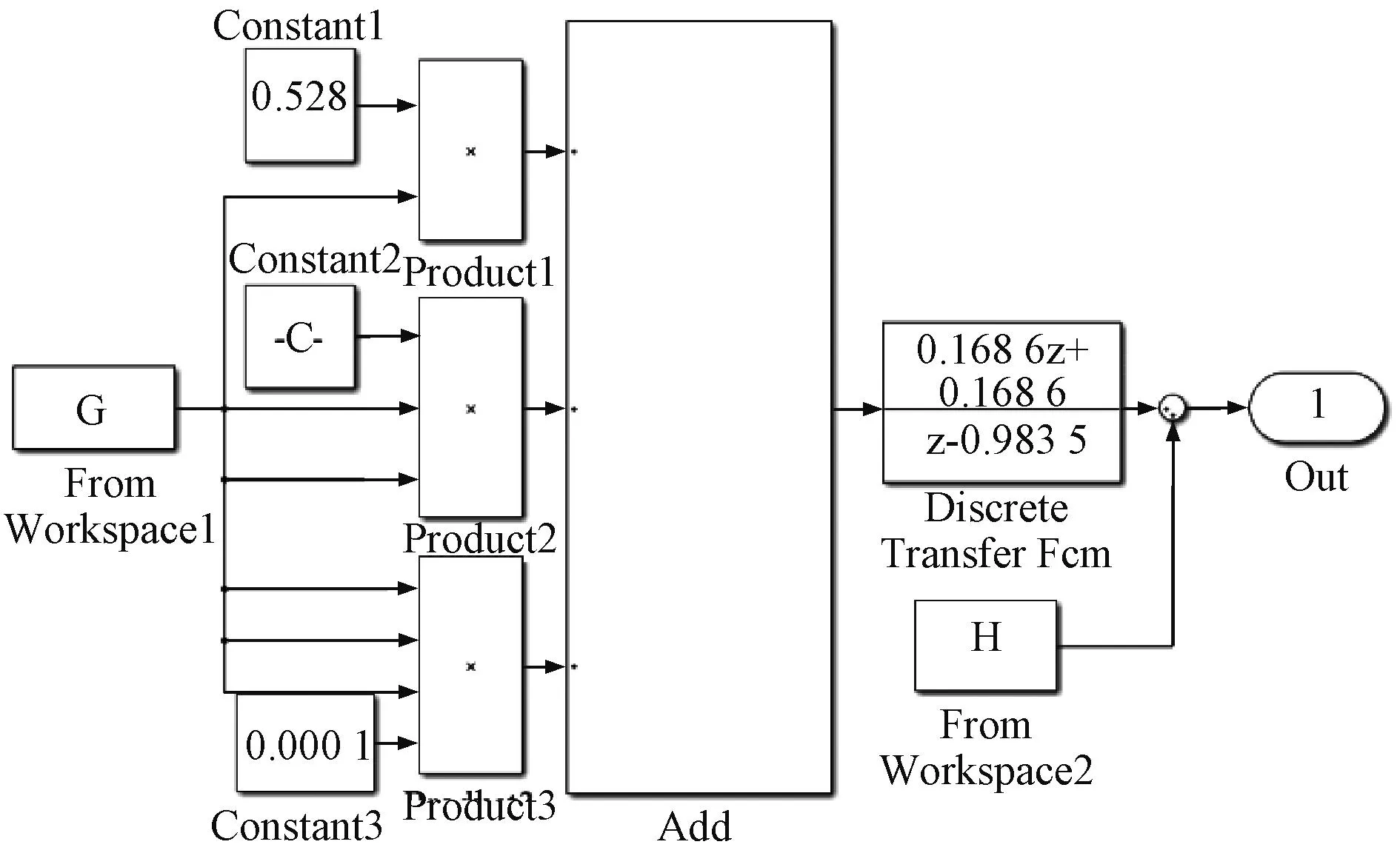
图5 再热汽温模型核心模块Fig.5 Reheat steam temperature model core module
3.1 参数设置
首先将PSO算法中的学习因子、惯性权重、速度范围等参数单独设置。其次为了不同算法之间的对比,将PSO算法的粒子的位置范围、最大迭代次数、种群数目等参数和SSA算法设置相同。而IPS算法各项参数同PSO算法和SSA算法设置相同。
3.2 实验结果及分析
在烟道挡板-再热器Hammerstein的模型中,三个算法辨识的模型输出与实际输出对比如图6所示。在图6中,根据辨识的再热器出口温度结果和再热器出口实际温度可以看出三条曲线与原始数据曲线基本相吻合,这表明PSO算法和SSA算法以及IPS算法都能够辨识烟道挡板-再热器Hammerstein模型的参数,但是PSO算法辨识的结果和实际值明显存在偏差,导致该曲线的辨识误差较大。
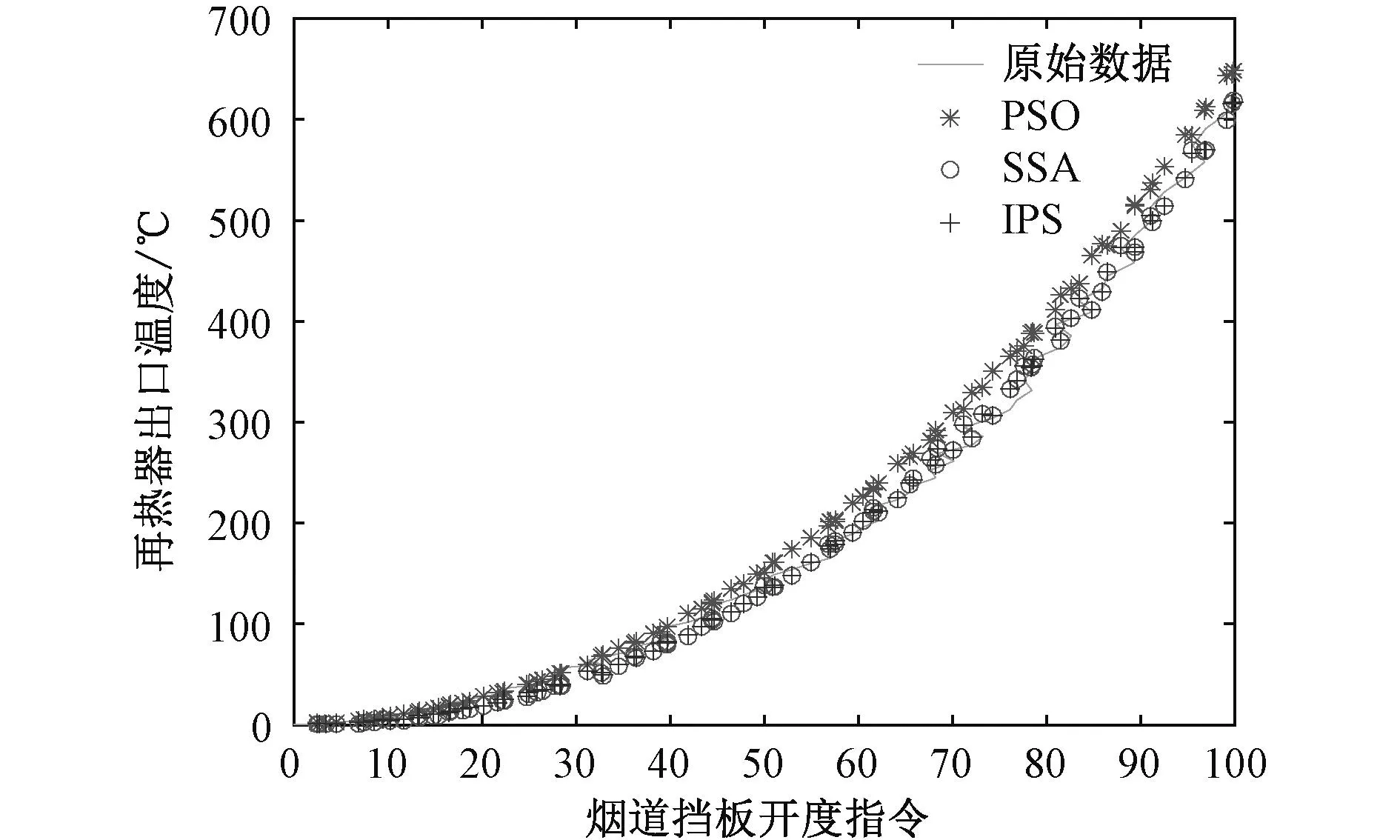
图6 不同算法的输出结果对比Fig.6 Compare output results of different algorithms
适应度函数J的优化过程如图7所示,从图中可以看出,三种算法的适应度函数值在迭代过程中逐渐趋于稳定。但是在前200次的迭代过程中,SSA算法的收敛速度比PSO算法和IPS算法的收敛速度慢,说明IPS算法能有效提高SSA算法辨识的速度。

图7 最佳适应度函数迭代过程Fig.7 Iterative process of optimal fitness function
PSO算法、SSA算法和IPS算法的最优参数辨识结果如表1所示。在表1中给出了实际参数值和三种算法辨识后的参数对比。从表1可以看出,在PSO算法中,参数r2与实际参数值的辨识误差相对于其他参数与实际参数值的辨识误差较大,而在SSA算法和IPS算法中,参数r2的辨识误差明显减少,其他参数的辨识误差也明显减少。

表1 不同算法参数辨识结果
从上述结果来看,无论是PSO算法还是SSA算法,都能通过建立Hammerstein模型的方法解决一些介质流量难以测量的执行机构非线性参数辨识问题,但IPS算法对参数的辨识精度更高,收敛速度更快,可以准确且快速的求取Hammerstein模型的各项参数。但由于受到现阶段电站控制系统的软硬件条件的限制,上述方法在工程实践中的在线实施需要一定的条件,所以现阶段所提方法主要适用于远程计算机的离线使用。
4 结 论
本文通过构建Hammerstein模型解决了流过执行机构的介质流量难以测量的非线性特性求取问题,并用PSO算法和SSA算法进行验证。另外,针对PSO算法陷入局部最优的问题以及SSA算法的前期收敛速度慢的问题,提出了改进的IPS算法。仿真结果表明,IPS算法对Hammerstein模型参数的辨识精度更高,收敛速度也更快,可以准确且快速的求取Hammerstein模型的各项参数。因此通过建立Hammerstein模型的方法能够解决流过执行机构的介质流量难以测量的执行机构非线性特性的求取问题,但是上述寻优算法的不确定性可能会导致所求非线性特性具有一定的误差。
