考虑负荷供电连续性的孤岛配电网负荷恢复策略

李 硕， 顾雪平

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

随着现代社会对电能供应依赖度的提高,如何保证可靠供电成为一个具有挑战性的问题。大规模输电系统难以避免地会发生各种事故,在区域电网互联而相互影响增大的情形下,可能导致连锁故障引发大规模停电事故[1-3]。输电网发生大停电故障时,传统的配电系统将因失去供电电源而造成停电,对人民生产生活产生巨大影响。随着配电网中新能源的接入和高级控制、测量装置的发展,配电网可对其包含的光伏、风电等分布式电源进行实时控制和测量[4],使得在上级输电网发生大停电事故的情况下由分布式电源保障本地主要负荷的电能供应,提高了供电可靠性,减小了因主网大停电带来的经济损失[5]。

国内外对配电网恢复进行了大量研究,从分布式电源自身特性出发,文献[6]考虑分布式能源独立维持孤岛运行的能力,并计及储能、电动汽车作为应急资源对系统恢复的影响,提出了考虑电动汽车配置的主动配电网鲁棒恢复模型。文献[7]考虑风电光伏等间歇性电源出力的不确定性,计及可控负荷的影响,利用可控负荷平衡间歇性电源出力波动,以最大化恢复负荷用电量为目标提出配电网短时恢复的供电策略。文献[8]提出了考虑分布式电源(DG)运行特性的孤岛划分策略,以保证配电网发生故障后关键负荷的供电。文献[9]考虑可调度和不可调度DG进行微电网划分。从负荷类型出发,文献[10]在传统负荷恢复策略的基础上,综合考虑可控负荷、重要负荷、分布式新能源占比、静态安全域和线路开关次数等因素,提出了计及可控负荷参与的主动配网动态恢复策略。文献[11]利用投入与产出确定负荷的失负荷价值,基于失负荷价值设置负荷权重,利用萤火虫算法进行求解。从恢复步长考虑,文献[12,13]基于固定时间步长考虑复电顺序约束,文献[14]进一步提出改进时间步长和变时间步长模型。

综上所述,传统配电网恢复研究所有负荷的整体供电情况,没有考虑单个用户负荷在总时段内的实际通电情况,极易因追求最大化恢复量而产生负荷单时段供电场景。由于新能源出力的波动性,当波动难以平抑时会频繁投切非重要负荷[15],极易产生非重要负荷短时段通电现象,导致负荷的连续供电需求无法保障,降低了非重要负荷供电可靠性。

针对负荷因平抑分布式电源出力波动的投切操作而导致的供电连续性无法保障问题,本文从单个负荷恢复角度出发,引入单负荷供电连续性系数,对连续多时段供电的负荷给予更高的权重,对单时段、双时段等短时供电场景给予较低的权重,使得负荷恢复时尽量减少短时段供电的场景,提高负荷供电的连续性和可靠性。

1 分布式电源及负荷时变模型

1.1 分布式电源

分布式电源包括风力发电机、光伏发电、储能电站、柴油机和燃气轮机等。输电网故障时配电网无法得到上级电网供电,可通过改变配电网的拓扑结构,协调其中的分布式电源,进行配电网的应急响应和负荷恢复,实现孤岛状态下配电网的灵活运行和可靠供电[16]。此时分布式电源可为重要电力负荷连续稳定供电,其出力的波动部分可以通过投切非重要负荷来进行平抑。

1.2 负荷时变模型

电力系统中负荷主要分为一级负荷、二级负荷、三级负荷。一级负荷停电将会造成重大经济损失、严重人身事故以及严重扰乱公共秩序;二级负荷停电将造成较大经济损失和公共秩序混乱;剩余的其它负荷是三级负荷。在配电网恢复过程中,一级负荷必须保障连续供电,二级负荷保证尽量连续供电,在一二级负荷恢复的基础上尽量恢复三级负荷。

本文根据配电网各节点的日负荷时变曲线,通过对每一个小时时段的日负荷曲线进行积分计算,即可得到各节点在某一时间段内的用电功率[17]。

(1)

式中:Wi(k)为i节点第k个时段的用电量;pi(x)为i节点负荷曲线函数。

将负荷分为民用、商用、工业三大类,其同一类负荷的用电需求趋势相同,因此考虑同一类负荷的用电需求系数近似相同。负荷不同时段所需有功功率可以通过用电需求系数与额定功率的乘积得到:

(2)

Pi(t)=αi(t)Pi,n

(3)

式中:Pi,n为i节点负荷额定功率;αi(t)为i节点t时段负荷用电需求系数;Pi(t)为i节点t时段负荷功率。

2 考虑负荷供电连续性的配电网恢复策略

先对配电网恢复时长进行估计,对故障时段内的分布式电源出力、负荷所需功率进行预测,在满足潮流约束、网络拓扑约束等约束的基础上合理开断线路,使得加权后的总恢复负荷最大。

2.1 目标函数

在传统配电网恢复以最大化恢复负荷量为目标的基础上,引入供电连续性系数Ci(t)来表示单个负荷供电的连续性程度。在重要负荷连续供电的前提下,从单个负荷供电角度出发,做以下定义:若负荷获得三个时段及以上的连续供电,则供电连续性系数为优;若获得两个时段连续供电,则供电连续性系数为良;若仅有单个时段供电,则供电连续性系数为差。通过引入供电连续性系数,使得寻优时在满足恢复最大负荷量的基础上,尽量使负荷连续供电,减少因分布式电源出力的波动而频繁投切负荷,延长负荷连续供电时长,提高供电可靠性。

目标函数为

(4)

式中:T代表恢复运行总时段数;Ci(t)为负荷供电连续性系数,其表示负荷i的供电连续情况,根据供电连续时段数可分为优、良、差三个级别;Ki(t)表示负荷i在时段t内是否供电,若负荷供电则取值为1,若不供电取值为0;ωi为负荷i的等级权重系数,一级负荷权重最高,二级负荷次之,三级负荷权重最低;Pi(t)为负荷i在t时段的有功功率大小。

负荷供电连续性指标Ci(t)取值可由下式确定:

当t>2时,

Ci(t)=

式中:Ci(t)代表负荷i在t时段的供电连续性系数;若t时段负荷供电,t-1时段不供电,则第t时段负荷供电连续性为差;若t时段与t-1时段负荷均供电,t-2时段不供电,则第t时段负荷供电连续性为良;若t时段、t-1时段、t-2时段负荷均供电,则第t时段负荷供电连续性为优。

当t≤2时,若负荷i第一个时段供电,则Ci(1)为差;若负荷i第一个时段与第二个时段均供电,则Ci(2)为良;若负荷i第一个时段不供电,第二个时段均供电,则Ci(2)为差。

2.2 约束条件

在目标函数的基础上,加入约束条件对寻优进行约束,使得结果满足配电网辐射结构、能量守恒定理、线路传输能力限制以及分布式电源出力限制。

1)潮流约束

配电网潮流可用distflow公式计算,但是其含有非线性部分的二次项,求解器无法对其进行求解,可用线性化方法对distflow公式进行简化,其二次项代表网损,因为其功率损耗远小于支路上流动的有功无功,因此忽略网损计算结果与原来结果近似,在配电网恢复问题中线性化的distflow公式已经被广泛应用[18,19],线性化的distflow公式如下:

(6)

(7)

(8)

(9)

(10)

2)线路容量、节点电压约束

线路流过有功无功不能超过线路实际传输容量,节点电压不能越限。

式中:D表示预定的数据包传输时延要求,即必须在时延D内将数据包传输至目的节点t。而elapsedtime表示数据包到达节点si已消耗的时间。因此,D-elapsedtime表示剩余时间remainingtime。

(11)

(12)

(13)

(14)

Vmin≤Vi≤Vmax

(15)

式中:Smax为线路最大容量;Vmax为节点电压最高限值;Vmin为节点电压最低限值。

3)网络辐射约束

配电网恢复要保证重构网络的辐射性和连通性,线路之间存在联络开关,其正常状态下保持断开状态,在重构过程中可能会因联络开关的闭合形成环网,因此在传统辐射网络约束的基础上,加入因为联络闭合而形成的环网集合,使得寻优过程中避开环网集合。

W=E+NS

(16)

Lm∉L′,m=1,2,….,M

(17)

式中:W为恢复节点总数;E为恢复支路总数;NS为孤岛数;M为环网集合数,其数值与联络开关数有关;Lm为第m个环网支路构成的集合;L′为全部闭合支路构成的集合,当所有环网集合均不全属于闭合支路集合时,就不会形成环网。

4)连通性约束

若当某相邻节点之间的支路选中时,其支路两端节点也会闭合,否则线路断开,这种逻辑关系与上述辐射约束共同作用,使得所有选中的节点和支路都相互连通。

Lij(t)≤Ki(t)

(18)

Lij(t)≤Kj(t)

(19)

式中:Lij(t)为0-1变量;若t时段节点i与节点j之间的线路闭合,则取值为1,反之为0;Ki(t)为0-1变量,若t时段节点i恢复则取值为1,反之为0。

5)节点、支路约束

当形成多个孤岛时,每个节点和支路只能属于某一个孤岛,通过约束使得所划分的孤岛相互独立。

(20)

(21)

6)分布式电源出力约束

实际分布式电源有功及无功出力不能超过其最大限值。

(22)

(23)

式中:Pmax,Pmin为分布式电源最大、最小有功出力;Qmax,Qmin为分布式电源最大、最小无功出力。

3 算例分析

本文采用改进PG&E69节点配电系统[17]算例,在yalmip中调用gurobi求解器进行求解。故障时段为7:00～15:00,系统额定电压为12.66 kV,总负荷有功功率为4 059.4 kW,总无功功率为2 865.9 kvar,虚线为网络联络开关,在节点9处接入额定功率为1 000 kW的DG1,在节点18处接入额定功率为900 kW的DG2。网络拓扑图如图1所示,其中虚线为联络开关;不同负荷类型的日用电需求如图2;分布式电源以光伏为例,不同时段出力标幺值如图3;负荷优先级分类如表1。

表1 负荷优先级

图1 PG&E69节点配电系统Fig.1 PG&E69node distribution system

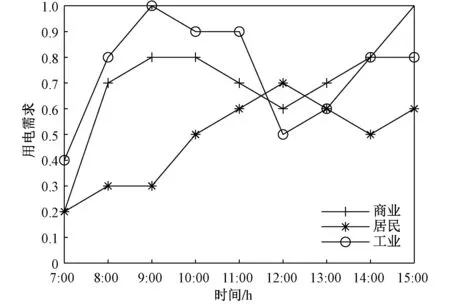
图2 不同负荷类型的日用电需求Fig.2 Daily electricity demand for different load types

图3 分布式电源出力标幺值Fig.3 Distributed power output standard value

将文献[20]目标函数作为对照组进行计算,和本文目标函数计算结果进行对比,对照组中是以恢复负荷的量最大作为目标函数。差、优、良供电连续性参数Ci(t)分别为1、3、6,对照组和本文恢复结果统计如表2、图4所示。两目标函数对一级负荷和二级负荷的恢复完全相同,其中一级负荷恢复比例为100%,二级负荷仅有22节点未恢复,其余二级负荷均恢复,节点22有功功率为1 kW,二级负荷总负荷量为550.6 kW,其恢复比例为99.82%。三级负荷恢复量由于本文目标函数中供电持续性指标的加入而有所不同。

表2 两种方法恢复结果统计

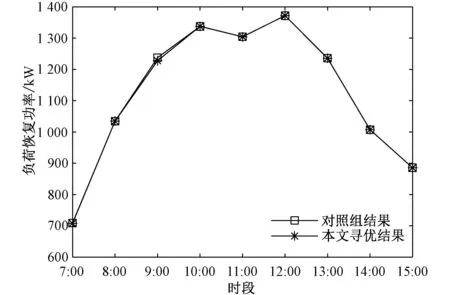
图4 两种方法不同时段恢复功率Fig.4 Recovery power of two methods in different periods

对照组共恢复负荷量10 124.94 kW,本文目标函数恢复负荷量为10 113.85 kW,占对照组总恢复的99.89%;对照组开关动作次数为88次,本文目标函数下开关动作次数为66次,占对照组总次数的75%。其中减少的负荷量是为了延长非重要负荷供电时长,非重要负荷由于分布式电源波动存在单一时段或双时段的短时供电问题,通过连续供电参数的介入,使得非重要负荷供电趋于连续,减少单一时段或双时段等短时供电场景产生,也使得开关状态趋向稳定,避免频繁开断。两种方法详细恢复结果如表3所示;本文方法第四时段恢复网架结果如图5所示,线路开关状态如图中实线所示,实现双孤岛运行。

表3 两种方法恢复结果

图5 第四时段恢复网架图Fig.5 Fourth period of restoration of the grid plan

提高供电连续性是以牺牲部分可恢复负荷为代价的,由于寻优更趋近于供电连续性,因此某单一时刻的可接通最大负荷必然因供电连续性系数影响转而接通计及供电连续性系数后更大的负荷节点。对照组目标函数只考虑供电量最大,因此本文比对照组恢复总供电量略低,但供电连续性大大提高。

将对照组与本文结果的供电连续情况进行对比,一级负荷和二级负荷在两结果中的连续性完全相同,此处不再进行赘述。剔除通电时长为连续三时段以上的三级负荷节点,剩余含有短时供电场景的情况如图6、7所示。对照组单时段供电数为10,双时段供电数为4;本文目标函数计算结果的单时段供电数为4,双时段供电数为0。经过供电连续性参数的引入,极大改变了非重要负荷供电不连续的问题,使得短时供电场景大大降低,提高了非重要负荷供电的可靠性。

图6 负荷单时段供电情况Fig.6 Single time supply situation of loads

图7 负荷双时段供电情况Fig.7 Double-time power supply situation of loads

4 结 论

本文提出了一种考虑负荷供电连续性的配电网负荷恢复方法,通过供电连续性参数Ci(t)的引入使得负荷恢复更加趋向于连续供电,大大减小了因为分布式电源波动而产生的短时(单时段或双时段)供电问题,同时使线路总投切次数降低,减少了开关设备的操作负担和维护成本。本文方法中,一部分负荷供电连续性的保障是以牺牲另一部分负荷的短时供电为代价的,在总体恢复负荷量相对最大的前提下尽量保证已恢复负荷的供电连续性,故与单纯以负荷恢复量最大为目标的恢复策略相比,总负荷恢复量略微减小(下降0.11%)。

供电持续性指标Ci(t)的大小反映了对负荷供连续性的要求,其值越大负荷恢复的结果更加趋于连续。Ci(t)的取值与分布式电源波动大小有关,分布式电源出力波动越大,则因波动导致负荷投切越频繁,供电间断性问题越突出,需适当增大Ci(t)的值,减少因波动产生的供电间断问题。需要进一步研究的是,如何评价分布式电源出力波动幅度对Ci(t)取值的影响,以实现负荷供电连续性与恢复负荷量最大化之间的协调优化。