基于改进蝙蝠算法的多目标移动储能调度

2024-04-17李永刚

华北电力大学学报(自然科学版) 2024年1期

李永刚，林卉

(华北电力大学电气与电子工程学院，河北保定 071003)

0 引言

环境污染和资源枯竭等问题日益严重,大力发展清洁能源已经成为世界各国应对该问题的共识。为实现“双碳”目标,构建以新能源为主体的新型电力系统,一方面,目前部分电网公司采用单一类型移动储能提供保供电、应急等服务,并未统筹协调多类型移动储能,并发挥其在配电网优化运行方面的作用,造成移动资源闲置与浪费;另一方面,电网中火电成本上升导致火力发电份额下降,而且新能源发电可靠性低、波动性强,加之冬季供暖等因素引起负荷激增,发电峰值期与负荷高峰期存在时空匹配度低的问题,出现配电网综合线损高、负荷峰谷差大等问题;“三北”地区经济发展相对滞后、电力需求不足,而化石能源和新能源都比较富足,风能与光能充足,即使火电机组全停仍有弃风弃光。随着可再生能源在配电网中渗透率的不断提升,其出力不确定性导致的弃风、弃光现象日趋严重。针对该问题,在高比例可再生能源背景下提出一种含三类移动储能协调调度的方法。

为平抑新能源发电功率的波动,储能技术受到广泛关注[1]。随着大容量储能电池[2]的出现、氢燃料发电车的兴起及电动汽车数量的高速增长,各类型移动储能资源[3]的容量及规模已达到支撑配电网优化运行的要求。近年来出现的全电驱动移动式储能兼具规模化储能和动态转移的能力[4],与传统的固定储能相比具有更高的灵活性。为了减少负荷峰谷差、降低网损,已有的研究对电动汽车参与调度的定价已经开展了不少的工作。文献[5]确定了电动汽车需求响应控制方法;文献[6]提出了一种在V2G模型下考虑供需双方需求的电动汽车日内调度策略;文献[7]提出了计及用户响应电价关联和多主体共赢的电动汽车充放电定价多目标优化方法。上述研究中并未计及交通能耗并进行电价补贴,仅考虑用户出行特性[8]设置电价。文献[9]提出了一种考虑风电概率的并网微电网能源优化调度新专家能源管理系统;文献[10]建立了一种考虑风力发电机和电动汽车的不确定性的契约模型;文献[11]提出了园区级能源互联网的能源效率优化调度。现有的研究对清洁能源发电的新型电力系统下的储能调度已有一定的研究,但并未涉及提高新能源利用率的优化调度。

文献[12]提出了一种基于移动储能的用于系统管理的提前一天能源管理系统;文献[13]提出了一种基于移动储能和电力交易的毫米波系统柔性增强策略。对于现有的与移动储能调度相关的研究中,均是对电动汽车、以卡车为载体的移动储能进行研究,且移动储能类型单一。

文献[14]研究了一种考虑用户满意度的负载聚合器参与的双层最优调度策略;文献[15]以微网运行成本和环境保护成本为目标建立微网经济调度模型。已有研究中并未涉及以负荷峰谷差、网损、新能源利用率、配电网运行成本四个指标为目标的调度模型。

针对上述问题,本文通过BP神经网络预测风力发电、光伏发电及需求侧负荷用电量确定移动储能充放电时间段,移动储能分为电动汽车、移动储能车、氢燃料发电车三类,计算移动储能前往充电站的交通能耗,针对电动汽车交通能耗,建立相应的补贴体系,以吸引电动汽车用户参与调度。其余类型则只计及交通能耗成本,不进行相应补贴。然后,建立以的配电网负荷峰谷差、新能源利用率、配电网运行成本为目标,利用超平面的概念自适应地确定不同目标函数的权重,将多目标归一化,建立三类移动储能协调调度模型。而后,使用改进蝙蝠算法求解,得到多类型移动储能协同调度的方案。其中,基本蝙蝠算法进行了K-means算法初始化、自适应步长速度更新、反向搜索、变异操作、引入高斯和柯西混合算子等改进,得到改进蝙蝠算法,该算法有效提升计算速度、优化速度、局部和全局搜索能力。

1 移动储能参与配电网优化运行调度的行为分析

1.1 移动储能参与配电网运行调度的方式

调度移动储能参与配电网运行,可减少负荷峰谷差、提高新能源利用率。电网调度中心根据24小时新能源、用电负荷预测功率,采集移动储能每一时段可参与调度功率、实时位置等信息,考虑负荷峰谷差、新能源利用率、配电网运行成本目标,优化移动储能24小时功率调度指令并下发给各移动储能,移动储能按照功率指令执行。

1.2 电网源荷特性

根据电网小时级风力发电功率、光伏发电功率、负荷功率的历史数据,采用BP神经网络[16]预测第二日新能源出力功率及负荷功率。基于文献[17]所提短期负荷预测模型,预测模型在一周的预测误差最小。

1.3 移动储能充放电调度

通过特定的软件获得所有移动储能的预约信息,其中包括下一时段移动储能是否参与调度,若参与调度可提供的功率及容量,对不同种类移动储能进行功率分配。移动储能在不同时段充电或放电取决于预测需求侧负荷大小、电动汽车随机充电功率、新能源发电利用率。

1.4 移动储能充放电交通轨迹及能耗

本文在移动储能调度模型中考虑了交通网络的实时路况信息[18],通过移动储能开始位置与充电站之间的最短路径结合实时路况信息计算移动储能前往充电站的交通能耗。A*算法[19]是启发式搜索算法中的一种,利用路径搜索算法,从移动储能设置的起点开始,搜索到目标点,计算相应的阻抗成本,最终可以得到成本最优的充电可行路径规划。

先通过交通路网确定移动储能行驶路线的数量及位置,以路口为交叉点,为每条路径标号,通过A*算法计算移动储能当前位置与充电站的距离,根据每公里电耗或油耗,求得移动储能的交通能耗。

1.5 移动储能运行特性建模

1)电动汽车

本文从电动汽车用户自身参与意愿的角度考虑,对电动汽车从实时位置至充电站这一路段中,对电动汽车的交通能耗进行直接的电价补贴,这一举措极大地提升了电动汽车参与调度的意愿,进而扩大了电动汽车时空及功率调度范围。

在可参与调度的电动汽车中同意参与下一时段调度的电动汽车功率总量如下:

(1)

(2)

配电网需要支付给参与充、放电调度的电动汽车的总成本如下:

(3)

(4)

电动汽车t时段参与调度总功率如下:

(5)

电动汽车调度流程如图1所示。

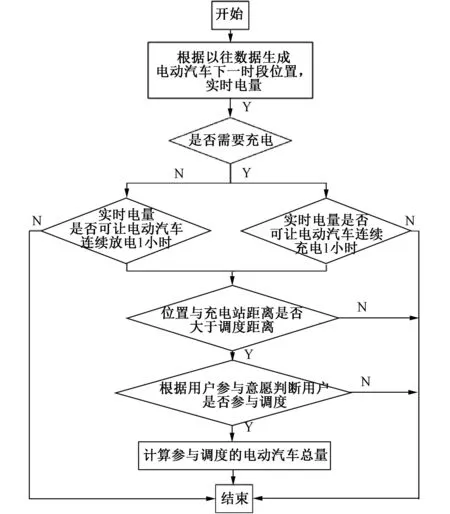
图1 电动汽车调度流程图Fig.1 Electric vehicle participation scheduling process

2)移动储能车

移动储能车为配电网资源,当移动储能车需要充当应急电源车时,在固定的位置进行应急供电,此时无法参与调度;当移动储能车处于闲置状态时,且其电量在可调度范围内时,可以参与调度,其前往充电站调度的距离同样可以用A*算法求解,以此得到交通能耗,由于移动储能车行驶为油耗,移动储能车参与调度的成本仅为充电成本与行驶油耗成本。移动储能车还需要作为应急电源车,根据以往数据,计算出移动储能车需要进行应急的时间段以及数量,在应急时段的移动储能车无法参与调度,而电量不足以充电1小时的移动储能车不参与充电调度,电量不足以放电1小时的移动储能车不参与放电调度。

t时段移动储能车充、放电总功率如下:

(6)

(7)

实际参与调度的移动储能车数量少于移动储能车总数与其参与调度的几率之积,t时段移动储能车参与调度的充电总成本如下:

(8)

移动储能车参与调度时,前往充电站行驶的油耗总成本与每公里油耗、行驶距离有关,移动储能车参与调度交通能耗成本如下:

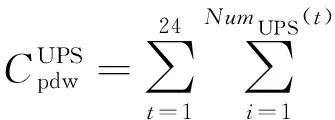
(9)

计算移动储能车每一时段的可调度容量流程如图2所示。

图2 移动储能车调度流程图Fig.2 Scheduling flow chart of mobile energy storage vehicle

3)氢燃料发电车

氢燃料发电车为配电网资源,但其仅能放电,其他步骤与移动储能车一致。

氢燃料发电车参与放电的总功率与氢燃料发电车的总量、参与调度几率、放电功率有关,计算如下:

(10)

氢燃料发电车充氢总成本与氢燃料发电车充氢单位成本、t时段实际参与放电调度的氢燃料发电车数量有关,氢燃料发电车充氢总成本计算如下:

(11)

氢燃料发电车参与调度时,前往充电站行驶的油耗总成本为每公里油耗与行驶距离之积,如下:

(12)

计算氢燃料发电车每一时段的可调度容量流程如图3所示。

图3 氢燃料发电车调度流程图Fig.3 Scheduling flow chart of hydrogen fuel generator vehicle

2 移动储能参与配电网优化运行的调度模型

2.1 目标函数

移动储能调度总功率如下:

(13)

式中:Pmess(t)为t时段移动储能调度总功率。

负荷峰谷差为峰值时段负荷与谷值时段负荷的差值,移动储能调度前后负荷峰谷差如下:

(14)

min[Plo(t)+Pmess(t)]

(15)

负荷峰谷差过大会有相应的负荷峰谷差惩罚成本,通过调度移动储能减少的负荷峰谷差惩罚成本如下:

(16)

通过调度移动储能减少负荷峰谷差所减少的负荷峰谷差惩罚成本如下:

(17)

新能源利用率如下:

(18)

式中:ηN(t)为新能源利用率。

通过调度移动储能减少的新能源弃电惩罚成本如下:

(19)

式中:fxny为配电网提高新能源利用率所得利润,ϑxny为新能源弃电单位惩罚成本,Pxin(t)为t时段减少的弃风弃光量。

以配电网运行成本最小为目标,计算公式如下:

(20)

式中:Pfpdw为配电网降低的运行成本。

当使用加权和方法求解多目标优化问题时,目标函数可视为在目标空间中运动的超平面。它的目的是寻找使不同目标的线性加权和值最小的最优解。超平面是比其周围空间小一维的子空间,如超平面是二维空间中的一条线,三维空间中的一个平面。本文利用超平面的概念确定自适应权值。目标函数定义为冲突目标函数Efgc、fxny、Profitpdw的线性加权和,超平面的斜率分别为权重值w1、w2、w3。为了在求解到平衡解前找到一个新的解,在该方法中,构造一个超平面来通过三个已知的解(q1、q2、q3),并使用超平面的系数作为下一个权值。通过求解矩阵形式的方程确定新的权值w1、w2、w3,如下所示:

(21)

其中第一个3×3矩阵包含已知解在目标空间中的位置,在已得到的权值基础上,逐步进行多目标优化,寻找新的最优解,从而得到最后的最优权重。

将多目标转换为单目标函数:

f=w1Efgc+w2fxny+w3Pfpdw

(22)

式中:f为最终求解的目标函数值。

2.2 约束条件

1)电动汽车充电电价约束

从配电网角度出发,为了引导更多电动汽车参与调度,必须设定合理的补贴电价。

ϑchmin≤ϑch(t)≤ϑchmax

(23)

ϑdismin≤ϑdis(t)≤ϑdismax

(24)

式中:ϑchmin、ϑchmax分别为电动汽车充电电价的最小、大值。ϑdismin、ϑdismax分别为电动汽车放电电价的最小、大值。

2)移动储能充放电功率约束

移动储能充放电功率必须小于等于最大值,如式(32)所示。

(25)

3 移动储能参与配电网优化运行调度模型的求解算法

基础蝙蝠算法随着算法迭代次数的增加,在以后的迭代中,群体的个体差异越来越大。群体的多样性越来越小,最终趋于零。在这方面,对基础蝙蝠算法进行了改进,并提出了一种改进蝙蝠算法。

1)K-均值算法初始化:先随机生成N只蝙蝠作为聚类中心,有多个聚类,重复随机生成N只蝙蝠,并将每只蝙蝠分成最近的一组,计算聚类中心,直到集群中心的变化区域小于给定阈值Δ,将最后的聚类中心输出为初始种群N中的蝙蝠个体。

2)自适应步长:提出了一种基于自适应步长的蝙蝠速度更新方法,蝙蝠速度根据以下公式更新如下,该算法的初始步长较大,从而提高了收敛速度。在算法的后期,步长变小,搜索得到细化。

(26)

(27)

式中:stepmin为最小步长,Tmax为最大的迭代次数,t为当前的迭代次数,K为系数。

3)反向搜索和变异

所有蝙蝠都按照适应度从高到低的顺序排列,选中适应度,最后一个蝙蝠排名N2,产生一个随机数字rand3值为0-1,当rand3>0.5时,根据公式(28)更新其位置,使种群向两个方向进化,从而增加种群的多样性。当0

(28)

(29)

式中:rand为0-1的随机数,xmax为蝙蝠的最大位置,xmin为蝙蝠的最小位置。

4)引入柯西变异逆累积分布函数

通过柯西逆累积分布函数对蝙蝠进行变异:

(30)

(31)

4 算例分析

4.1 算例参数

本文选取IEEE 33节点电网为例对充放电场景进行仿真验证。建立仿真场景,以中国某地区的负荷、风力发电、光伏发电数据为例进行分析。以一天24小时为一个周期,时间尺度为1小时。电动汽车以比亚迪e6[20]为研究对象,充放电功率为7 kW,电池容量为82 kW·h。移动储能车的充放电为功率100千瓦,电池容量450千瓦时。氢燃料发电车的额定输出功率为110千瓦,单台氢燃料发电车的输总容量为700 kW·h。

4.2 算例结果

分别对以下6种场景进行仿真研究。

表1 6种场景

图4 移动储能参与调度功率Fig.4 Mobile energy storage participating in power dispatching

图4分别为场景1～6的移动储能参与调度功率分布图,除场景2为单一类型移动储能参与调度外,其余场景均为三类移动储能参与调度,蝙蝠算法和改进蝙蝠算法求解的场景中移动储能车和氢燃料发电车参与调度的功率远大于电动汽车的功率,这是由于求解多目标函数时,权重会改变,当权重不同时,移动储能参与调度的功率分配也会不同。从整体来看,移动储能的种类与数量越多,移动储能的利用率越高,参与调度功率越大。

参考表2的数据,其中场景1、2的削峰填谷效果最差,可以得知当移动储能类型单一或移动储能数量较少时,负荷峰谷差的减少量较小。对比场景3、4、6可以看出,用改进蝙蝠算法求解的削峰填谷效果最优,蝙蝠算法求解的效果最差。总的来讲,移动储能数量与种类越多,削峰填谷的效果越好,且由改进蝙蝠算法求解的效果最优。

表2 不同场景下的负荷峰谷差

参考表3的数据,当仅有电动汽车参与调度和由蝙蝠算法求解时,弃风弃光不仅没有减少,反而增加了,这是因为在求解多目标函数时,多目标的自适应权重会改变,因此出现了弃风弃光量增加的情况。当计及交通能耗时弃风弃光降低量要低于不计及交通能耗的降低量。总的来说,多类移动储能参与调度、计及交通能耗并用改进蝙蝠算法求解时弃风弃光量最小。

表3 不同场景下弃风弃光量

由表4可以看出,由于电动汽车参与调度时时,配电网的成本最高,仅由电动汽车参与调度时降低的运行成本是最小的。当移动储能类型单一时,降低的运行成本远低于多类型移动储能协调调度。使用不同算法求解时,改进蝙蝠算法求解的效果最佳。总的来讲,由多类移动储能参与调度、计及交通能耗并用改进蝙蝠算法求解时配电网调度后降低的运行成本最多。