构网型并网逆变器状态空间建模及稳定性分析
2024-04-17刘淇玉李永刚吴滨源黄齐林张梦琪
刘淇玉, 李永刚, 王 月, 吴滨源, 黄齐林, 张梦琪
(1.新能源电力系统国家重点实验室(华北电力大学),河北 保定 071003;2.国网江苏省电力有限公司南通供电分公司,江苏 南通 226006)
0 引 言
并网逆变器是新能源发电单元接入电力网络的重要接口元件[1]。随着“30·60碳达峰、碳中和”目标的提出与逐步实施[2],以风电、光伏为代表的可再生能源渗透率大幅提升,多种类、多工况运行的并网逆变器在现代“双高”(高比例可再生能源和高比例电力电子化设备)电力系统中应用也愈加广泛[3]。受并网逆变器多尺度控制耦合影响,其与电网阻抗形成复杂交互,稳定性问题凸显[4],严重危害电力系统安全稳定运行,亟需开展相关研究[5]。
现有并网逆变器按并网属性可分为:跟网型并网逆变器和构网型并网逆变器两类[6]。文献[7]在同步控制器、内环控制器、摇摆特性和电网强度等方面阐述两类逆变器的对偶特性;文献[8]探讨了两类并网逆变器与同步发电机间的耦合机理;文献[9]介绍了适用于两类并网逆变器的控制技术,一种是P-Q下垂控制,另一种是V-F控制。
跟网型并网逆变器通过锁相环跟随电网电压相角,采用电流PI控制调节交流侧并网电流,其控制简单高效,在现代电力系统中应用广泛。然而,弱电网下[10,11],受锁相环带宽影响,并网逆变器、锁相环和电网间存在耦合,使系统易失去同步并由此引发稳定性问题。
构网型并网逆变器通过功率控制环追踪电网相角变化,借助电压PI控制器实现对交流侧并网电压的实时控制,在弱电网中较跟网型并网逆变器表现出更强的适应性[12]。然而,文献[13-14]指出:构网型并网逆变器在强电网中也存在稳定性问题。文献[15]对构网型并网逆变器进行稳定性分析,证明逆变器的电压和频率是以分散和自治的方式调节和控制的,并且遵循一种类似于下垂的非线性行为。
现有并网逆变器稳定性分析方法包括:基于阻抗的稳定判据和基于状态空间模型的参与因子分析[16]。基于阻抗的稳定判据将并网逆变器和电网划分为两个独立子系统,分别获取其等效阻抗[17],通过Nyquist曲线对并网逆变器系统进行判稳。然而,该方法无法确定引起系统失稳的关键设备甚至控制环节。基于状态空间模型的参与因子分析[18]首先计算系统状态矩阵特征值,通过判断特征值实部是否为正来评估系统稳定性[19],然后计算各状态变量参与因子值,系统设计者或设备厂商可由此重调控制参数,从而使系统恢复稳定。因此,基于状态空间模型的参与因子分析较基于阻抗的稳定判据更受研究人员青睐。
目前,关于构网型并网逆变器建模文献较少,基于状态空间模型对并网逆变器稳定性的分析也不够深入,针对这一空缺,本文对构网型并网逆变器的状态空间建模和稳定性分析问题开展研究,主要贡献总结如下:(1)详细呈现构网型并网逆变器状态空间建模的相关细节,包括功率控制环、电压控制环、时滞环节和LCL滤波环节;(2)对强电网下构网型并网逆变器失稳现象进行了复现,并基于所提模型开展参与因子分析,验证模型有效性;(3)基于模型对构网型并网逆变器主要环节参数变化引起的失稳问题进行分析。
基于上述分析,本文以构网型并网逆变器为分析对象,建立构网型并网逆变器的状态空间模型,通过求解特征值分析并网逆变器系统稳定性。搭建IEEE 4节点典型系统仿真,验证本文模型的有效性和实用性。
1 构网型并网逆变器模型建立
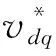

图1 构网型并网逆变器典型拓扑Fig.1 Typical topology of grid-forming inverter
1.1 基于下垂控制的功率控制环建模
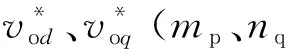

图2 基于下垂控制的功率控制环结构Fig.2 Power control loop based on droop control
基于下垂控制的功率控制环状态空间模型可以通过组合功率计算器模块、低通滤波器和下垂控制器来实现,如式(1)所示。
(1)
式中:vp= [vod,voq,iod,ioq]T,xp= [P,Q]T,γp= [ω]T,
式中:vodq0和iodq0:电压工作点和电流工作点。
1.2 电压控制环节
图3为一个经典的基于PI控制的电压控制环,根据输入的电压指令输出电流指令。电压控制环状态方程与输出方程可根据其结构示意图表示如下:

图3 电压控制环结构Fig.3 Voltage control loop structure
电压控制环状态空间模型如式(2)~式(4)所示:
(2)
(3)
(4)
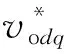
式(2)~(4)可通过线性化方式得到其状态空间模型,如式(5)~(6)所示。
Δφdq=
BV2[Δildq,Δvodq,Δiodq]T
(5)
(6)
式中:
1.3 时滞环节
图1所示结构中,电压信号经过硬件设备后会产生延时,可由式(7)表示:
v=e-τ·sv*
(7)
式中:v*为未经过硬件设备的电压信号值;v为经过硬件设备后产生延时的电压信号值;τ= 1.5Ts为数字计算延迟(Ts)和脉宽调制延迟(0.5Ts)产生的延迟时间;Ts为逆变器采样周期。
为了评估延迟环节对系统稳定性的影响并揭示状态之间的相互作用,采用Pade近似将时滞指数项等效为式(8)所示的传递函数,用于在状态空间模型中进行特征值分析。
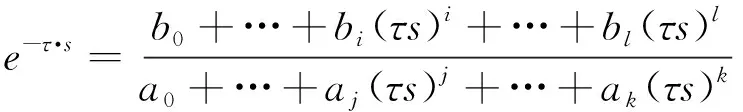
(8)
(9)
(10)
式中:l、k分别为Pade近似中的阶数。
为分析时滞环节中各因素之间联系,式(8)可进一步转换为状态空间表达式如式(11)所示:
(11)
(12)
1.4 LCL滤波环节
由滤波器结构可列写滤波器及其和逆变器耦合电感的状态方程,如式(13)~(18)所示:
(13)
(14)
(15)
(16)
(17)
(18)
式中:Lf为滤波器电感;Cf为滤波器电容;Rf为滤波器电阻;Lc为滤波器与逆变器间耦合电感;vbdq是连接逆变器的母线电压;ω为逆变器输出电压的角频率。将母线电压vbdq和角频率ω视为逆变器的输入变量。
式(13)~(18)经线性化后可由式(19)所示。
(19)
式中:
2 理论基础
2.1 特征值分析
特征值分析对研究线性系统稳定性有着良好的效果,该方法通过计算系统状态空间表达式的特征值并将计算结果绘制在坐标系中而判定系统的稳定性,其中,该坐标轴虚轴表示振荡频率,实轴表示稳定区域。若特征根位于左半平面(即特征根实部为负),则判定系统稳定;若特征根位于右半平面(即特征根实部为正),则判定系统不稳定。可根据系统参数的改变绘制不同的特征根点,不同特征根点形成的变化轨迹称为系统的根轨迹。
2.2 参与因子分析
为了揭示系统不同组件对于谐波稳定性的影响,实现不稳定分量的定位溯源,本文利用参与因子建立状态变量、系统参数与系统不稳定模式之间的映射关系,通过计算不稳定模式下不同状态变量的参与程度,获取不同组件参数信息。定义第k个状态变量和第i个特征值的参与因子pki如式(20)所示:
(20)
式中:λi为第i个特征值;ak为第k个状态变量;uik为左特征向量元素;vji为右特征向量元素。
式(20)可进一步表达为式(21)~(22):
p=[p1,p2,…,pn]
(21)
p1=[p1i,p2i,…pni]T=[u1ivi1,u2ivi2,…univin]T(22)
式中:右特征向量矩阵和左特征向量矩阵被定义为U=[u1i,u2i,…,uni]T,V=[vi1,vi2,…,vin]。uki是指右特征向量矩阵U的第k行和第i列上的元素,用于测量第k个状态变量在第i个模式中的相对参与度。vik是指左特征向量矩阵V第i行和第k列上的元素,可以评估该分量对模式的贡献。
3 算例介绍
3.1 系统说明
结合前述功率控制控制环、电压控制环、时滞环节和LCL滤波环节的状态空间表达式,建立单个构网型并网逆变器状态空间表达式如式(23)所示:
(23)

3.2 系统建模
建立三相逆变器并网系统,该系统包括逆变器单元、线路和负载,具体拓扑结构如图4所示。
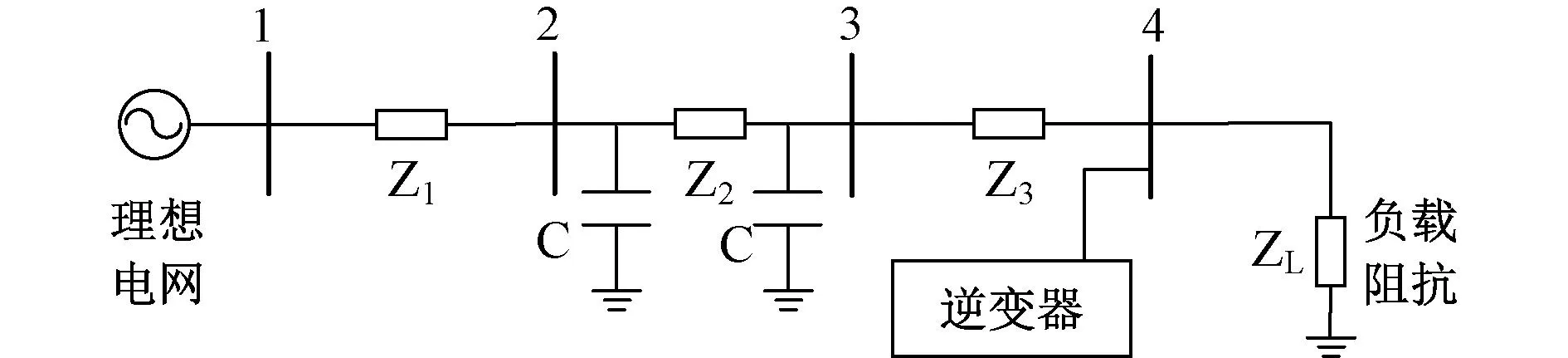
图4 典型三相逆变器并网系统单相等效电路Fig.4 Single phase equivalent circuit of typical three-phase inverter grid connected system
建立整个系统的小信号模型需建立线电流和负载电流的线性化方程,整体小信号状态空间模型可以如式(24)所示:
(24)
式中:Δx为整个微电网的状态向量;A为状态矩阵,Δx=[Δxinv,Δiline1,Δiline2,Δiline3,Δiload];Δiline1、Δiline2和Δiline3为第1条线路、第2条线路和第3条线路的电流状态;Δiload为负载线路的电流状态。
系统控制器参数与初始工作点分别如表1、表2所示。
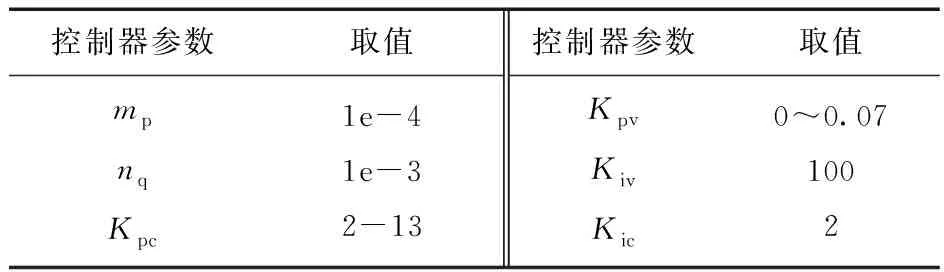
表1 状态空间模型中的控制器参数
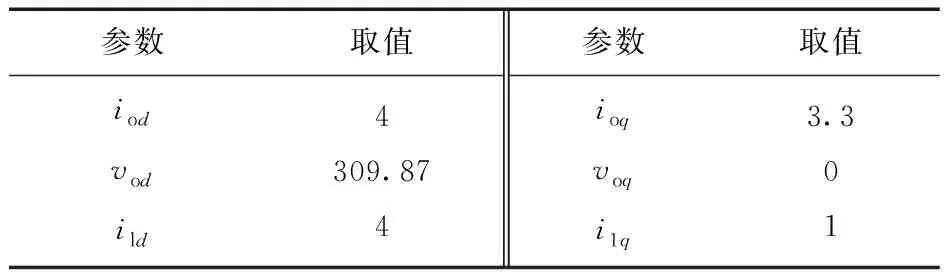
表2 三相逆变器并网系统初始稳态运行点
3.3 强电网下构网型并网逆变器稳定性分析
本文所建立的三相逆变器并网系统为单馈入系统,本文参考文献[22],定义短路比(Short Circuit Ratio, SCR)交流短路容量与电力电子设备的额定容量的比值,如式(25)所示:
(25)
式中:Sac为交流系统的短路容量;Prated为新能源并网逆变器额定功率;Id_rated为新能源并网变换器额定电流;Ug为电网母线额定电压;Xg为公共耦合点与电网间等效阻抗。
短路比对系统稳定性判定具有重要意义,SCR越大,电网越强。认为小干扰稳定意义下的临界短路比(Critical Short Circuit Ratio,CSCR)如下:单馈入系统出现实部为0的特征值时,系统处于临界稳定状态,此时系统对应某一短路比,该短路比即为该单馈入系统小干扰稳定意义下的临界短路比。
图4所示系统所用新能源并网逆变器额定功率为10 kW,电网电压为380 V,经过计算得到电抗与短路比间换算关系如表3所示。
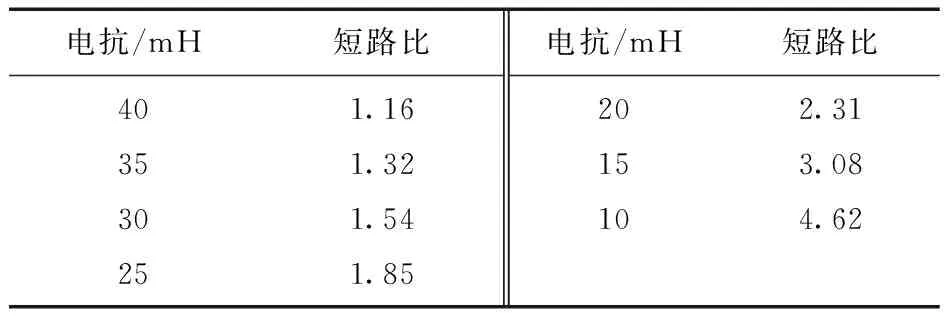
表3 系统电抗与短路比间换算关系
图5由弱电网到强电网获得的状态空间模型根轨迹曲线。从图5的全局图中可以看出:当SCR由1.16变化至4.62时,系统状态空间模型的特征值也发生变化,逐渐向右半平面偏移。这说明:随着电网性质由弱电网变为强电网,系统逐渐失稳。从图5的局部图中看出,显著特征值(主要引起稳定性变化的特征值)从蓝色加号(对应SCR=1.16时)移动至深红色菱形点(SCR=4.62时),其中,蓝色加号位于左半平面(此时系统处于稳定状态),特征值向右半平面偏移的过程中第一个进入右半平面的为绿色叉号(此时系统刚由稳定状态变为不稳定状态),深红色菱形点位于右半平面(此时系统处于不稳定状态)。以上分析说明了随着电网性质由弱电网变为强电网,系统状态空间模型的特征根值向右半平面移动,系统趋于不稳定状态。
令该系统特征值实部为0,经计算可得对应电抗值为23 mH,对应SCR为2.01,由前述理论可知,该系统临界短路比即为2.01。

图5 由弱电网到强电网的系统稳定性变化Fig.5 Influence of line impedance on system stability
在所建立的单个构网型并网逆变器中,各元件对系统谐波不稳定性的影响程度由对应的状态变量进行表征,因经大部分状态变量所表征的元件参与程度较低,故选取参与程度较高的元件(主要参与元件)进行分析,其与状态变量的表征存在如下的对应关系:表征电网性质由状态变量iload表征,功率控制环参与程度由状态变量xp表征,电压控制环参与程度由状态变量vo表征,时滞环节参与程度由状态变量xd表征。经过计算的各情况下参与因子(结果保留至小数点后两位)见表4~表7所示。
表4为未改变参数前原系统各状态变量计算得到的初始参与因子,表5~表7分别为改变短路比、改变下垂控制增益和改变电压环控制增益后系统各状态变量计算得到的参与因子。通过改变系统参数计算得到各状态变量的参与因子并与初始参与因子进行比较,可以得知改变系统参数后各状态变量对应计算的参与因子变化值,从而反映各状态变量表征的元件参与程度。

表4 原系统各状态变量初始参与因子
由表4可知,未改变系统参数前,通过状态变量iload计算得到的初始参与因子值为0.11,通过状态变量xp计算得到初始参与因子值为0.24,通过状态变量vo计算得到初始参与因子值为0.19,通过状态变量xd计算得到初始参与因子值为0.21。
由表5可知,改变短路比后,通过状态变量iload计算得到的参与因子值较初始参与因子值增大0.08,通过状态变量xp计算得到的参与因子值较初始参与因子值减小0.07,通过状态变量vo计算得到的参与因子值较初始参与因子值减小0.04,通过状态变量xd计算得到的参与因子值较初始参与因子值减小0.03,这表明改变短路比后,线路阻抗参与程度有所增加,功率控制环节、电压控制环节和时滞环节参与程度减小,其中iload参与因子变化量最大,参与因子值也最大,这说明改变短路比后,线路阻抗在系统的参与程度最多,即线路阻抗是电网由弱电网变为强电网过程中影响谐波不稳定性的主要元件。

表5 改变短路比后各状态变量参与因子
4 不同参数变化下系统稳定性分析
图6为改变下垂控制增益获得的状态空间模型的根轨迹曲线,其中下垂控制增益由m表示。从图6的全局图中可以看出:m从0.5到3.5的变化过程中,系统状态空间模型的特征值也发生变化,逐渐向右半平面偏移。这说明:随着m的增大,系统趋于不稳定状态。从图6的局部图中看出,显著特征值从蓝色加号(对应m=0.5时)移动至深红色菱形点(m=3.5),其中,蓝色加号位于左半平面(此时系统处于稳定状态),特征值向右半平面偏移的过程中第一个进入右半平面的为紫色点(此时系统刚由稳定状态变为不稳定状态),深红色菱形点位于右半平面(此时系统处于不稳定状态)。以上分析说明了随着m的增大,系统状态空间模型的特征根值向右半平面移动,系统逐渐失稳。
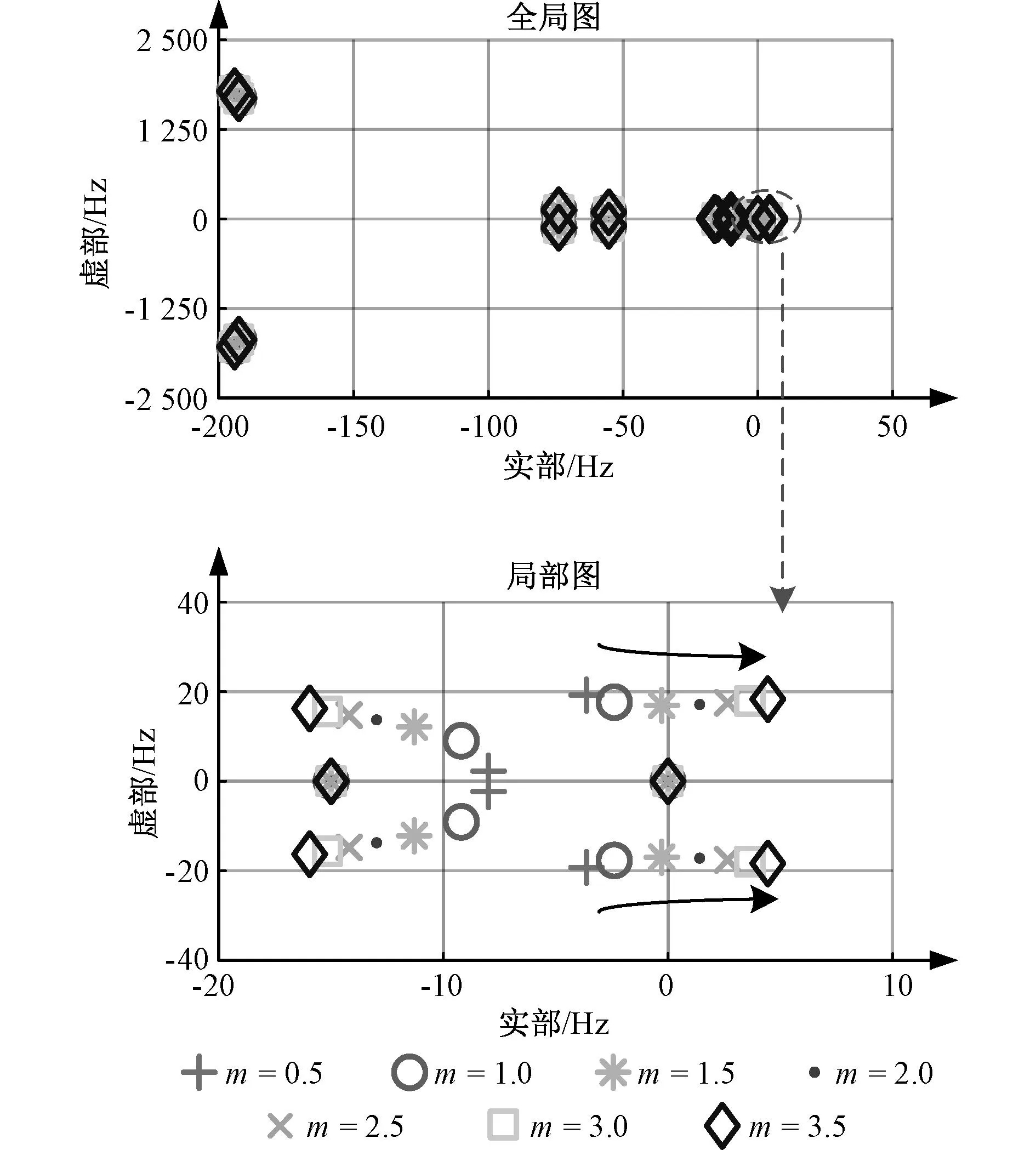
图6 下垂控制增益对系统稳定性影响Fig.6 Influence of droop control gain on system stability
由表6可知,改变功率控制环下垂控制增益后,通过状态变量iload计算得到的参与因子值较初始参与因子值减小0.02,通过状态变量xp计算得到的参与因子值较初始参与因子值增大0.07,通过状态变量vo计算得到的参与因子值较初始参与因子值减小0.07,通过状态变量xd计算得到的参与因子值较初始参与因子值减小0.02,这表明改变功率控制环下垂控制增益后,功率控制环参与程度有所增加,线路阻抗、电压控制环和时滞环节参与程度减小,其中xp参与因子变化量最大,参与因子值也最大,这说明改变下垂控制增益后,功率控制环在系统的参与程度最多,即功率控制环是影响谐波不稳定性最主要的元件。

表6 改变下垂控制增益后各状态变量参与因子
图7为改变电压环控制增益n获得的状态空间模型的根轨迹曲线。从图7的全局图中可以看出:当n由1.1变化至0.5时,系统状态空间模型的特征值也发生变化,逐渐向右半平面偏移。这说明:随着n的减小,系统逐渐失稳。从图7的局部图中可以看出,显著特征值从蓝色加号(对应n=1.1时)移动至深红色菱形点(对应n=0.5时),其中,蓝色加号位于左半平面(此时系统处于稳定状态),特征值向右半平面偏移的过程中第一个进入右半平面的为绿色叉号(此时系统刚由稳定状态变为不稳定状态),深红色菱形点位于右半平面(此时系统处于不稳定状态)。以上分析说明了随着电压环控制增益的减小,系统状态空间模型的特征根值向右半平面移动,系统趋于不稳定状态。

图7 电压环控制增益对系统稳定性影响Fig.7 Influence of voltage loop control gain on system stability
由表7可知,改变电压控制器电压环控制增益后,通过状态变量iload计算得到的参与因子值较初始参与因子值不变,通过状态变量xp计算得到的参与因子值较初始参与因子值减小0.03,通过状态变量vo计算得到的参与因子值较初始参与因子值增大0.09,通过状态变量xd计算得到的参与因子值较初始参与因子值减小0.03,这表明改变电压环控制增益后,电压控制器参与程度有所增加,线路阻抗、功率控制环节和时滞环节参与程度都有所减小,其中vo参与因子变化量最大,参与因子值也最大,这说明改变电压环控制增益后,电压控制环在系统的参与程度最多,即电压控制环是影响谐波不稳定性的主要元件。
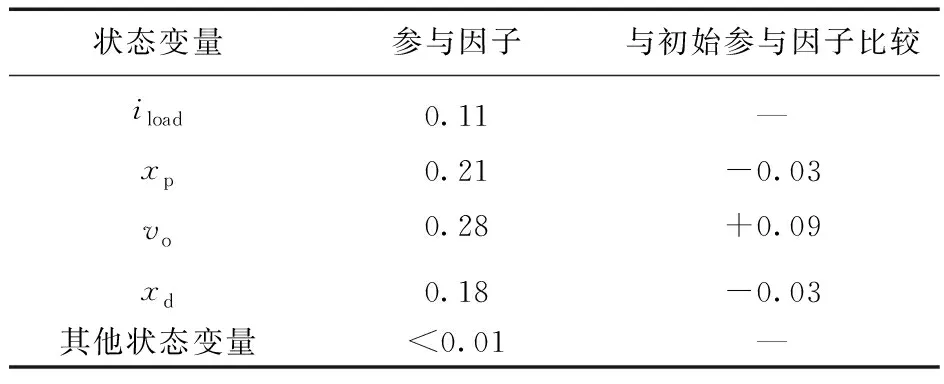
表7 改变电压环控制增益后各状态变量参与因子
5 实验结果分析
如图4所示,本文以改进型的IEEE 4节点三相平衡电网系统为算例,考虑逆变器阻抗、下垂控制增益和电压环控制增益,分析系统在不同参数下的稳定性。
5.1 实验平台概述
基于图4所示的并网逆变器系统,在Simulink中搭建并网逆变器实时仿真模型,其中模型具体参数如表1所示,模型初始稳态运行点如表2所示,仿真时间为3 s。上位机处理器参数为:2.5 GHz Intel Core i5。
5.2 实验结果分析
图8选取了SCR=1.16、SCR=2.31和SCR=4.62三种短路比情况下,系统由稳定状态转为不稳定状态的三个关键点,绘制了系统由弱电网变为强电网过程中不同稳定状态下的电压波形曲线。由图8(a)可知,当SCR=1.16时,系统输出的电压波形为标准的正弦波形,波动范围较小,这说明SCR=1.16时,系统处于稳定状态。由图8(b)可知,当SCR=2.31时,系统输出的电压波形不再是标准的正弦波形,而是没有固定周期的大幅波动波形,电压波形波动的最小幅值和最大幅值有较大的差值,在采样时间为1.12 s和1.22 s附近时,电压波形幅值有减小的过程,即系统试图达到稳定状态,但最终仍然走向不稳定状态,符合理论分析中SCR=2.31时系统刚刚失稳的特点。由图8(c)可知,当SCR=4.62时,系统输出的电压波形也不是标准的正弦波形,电压波形波动的最小幅值和最大幅值差值不大,对比SCR=2.31时的电压波形曲线,SCR=4.62时的电压波形波动起伏更大,且整个系统没有试图达到稳定状态的迹象,这说明,SCR=4.62时,系统彻底失稳。根据特征值分析获取到的三个显著特征值对应输出的电压波形可以得知,针对特征值做出的理论分析是正确的,即系统搭建模型也是正确的。
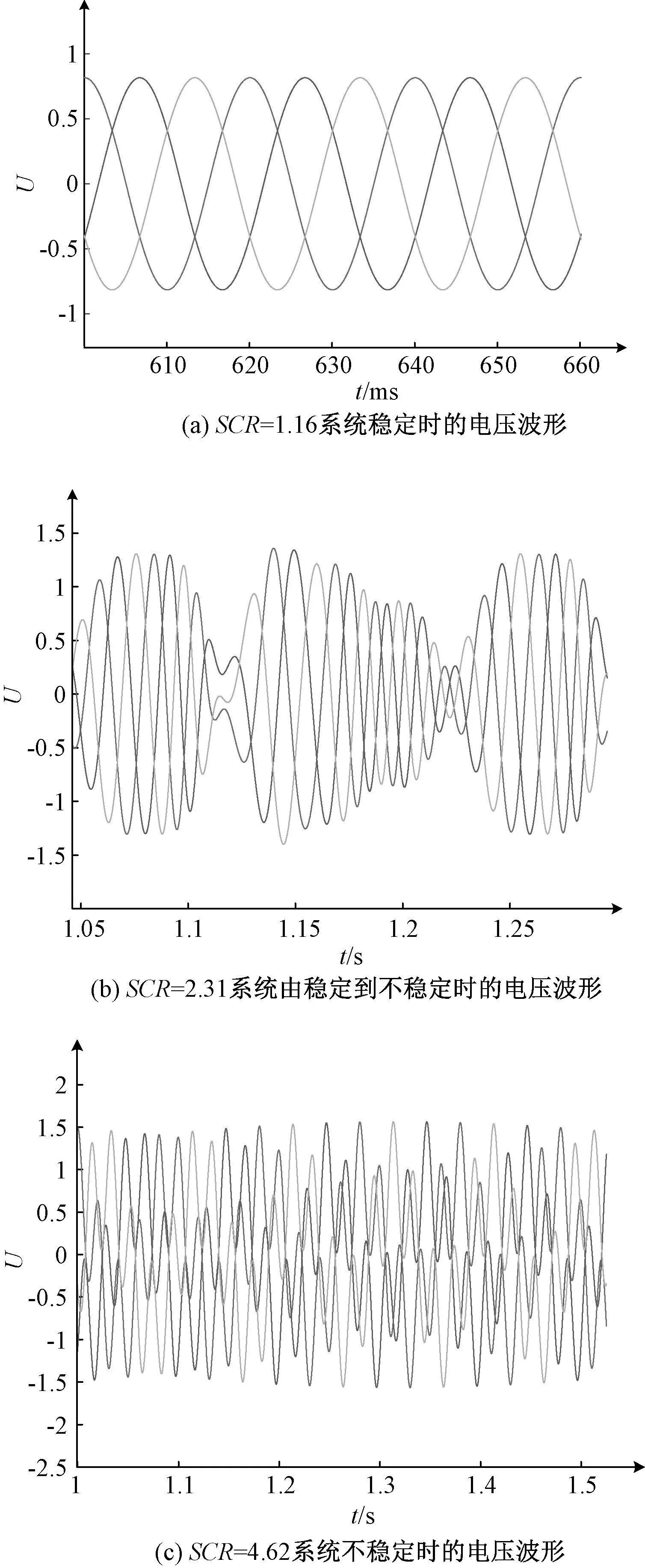
图8 改变短路比情况下系统不同稳定状态的电压波形Fig.8 Voltage waveforms of different steady states of system under condition of changing line impedance
图9选取了m=0.5、m=2.0和m=3.5三种下垂控制增益情况下,系统由稳定状态转为不稳定状态的三个关键点,绘制了系统不同稳定状态下的电压波形。由图9(a)可知,当m=0.5时,系统输出的电压波形为标准的正弦波形,波动范围较小,这说明m=0.5时,系统处于稳定状态。由图9(b)可知,当m=2.0时,系统输出的电压波形不再是标准的正弦波形,而是没有固定周期的波动波形,电压波形波动的最小幅值和最大幅值有较大的差值,在采样时间为1.5 s和1.56 s附近时,电压波形幅值有减小的过程,即系统试图达到稳定状态,但最终仍然走向不稳定状态,符合理论分析中m=2.0时系统刚刚失稳的特点。由图9(c)可知,当m=3.5时,系统输出的电压波形也不是标准的正弦波形,电压波形波动的最小幅值和最大幅值差值不大,对比m=2.0时的电压波形曲线,m=3.5时的电压波形波动起伏更大,且整个系统没有试图达到稳定状态的迹象,这说明,m=3.5时,系统彻底失稳。根据特征值分析获取到的三个显著特征值对应输出的电压波形可以得知,针对特征值做出的理论分析是正确的,即系统搭建模型也是正确的。

图9 改变下垂控制增益情况下系统不同稳定状态的电压波形Fig.9 Voltage waveforms of different steady states of system under condition of changing droop control gain
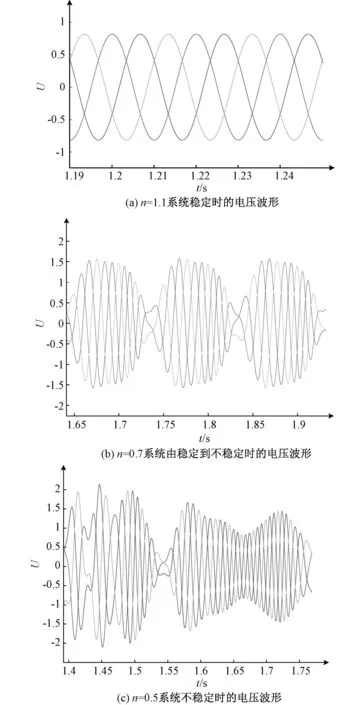
图10 改变电压环控制增益情况下系统不同稳定状态的电压波形Fig.10 Voltage waveforms in different steady states of system under condition of changing voltage loop control gain
图10选取了n=1.1、n=0.7和n=0.5三种电压环控制增益情况下,系统由稳定状态转为不稳定状态的三个关键点,绘制了系统不同稳定状态下的电压波形。由图10(a)可知,当n=1.1时,系统输出的电压波形为标准的正弦波形,波动范围较小,这说明n=1.1时,系统处于稳定状态。由图10(b)可知,当n=0.7时,系统输出的电压波形不再是标准的正弦波形,而是没有固定周期的波动波形,电压波形波动的最小幅值和最大幅值有较大的差值,在采样时间为1.74 s和1.84 s附近时,电压波形幅值有减小的过程,即系统试图达到稳定状态,但最终仍然走向不稳定状态,符合理论分析中n=0.7时系统刚刚失稳的特点。由图10(c)可知,当n=0.5时,系统输出的电压波形也不是标准的正弦波形,电压波形波动的最小幅值和最大幅值仍有不小的差值,对比n=1.1时的电压波形曲线,n=0.7时的电压波形波动起伏更大,这说明,n=0.5时,系统更加趋于不稳定状态,但仍未完全失稳,若继续减小电压环控制增益,则系统会彻底失稳。根据特征值分析获取到的三个显著特征值对应输出的电压波形可以得知,针对特征值做出的理论分析是正确的,即系统搭建模型也是正确的。
6 结 论
本文针对构网型并网逆变器状态空间模型的相关细节和基于状态空间模型的稳定性分析问题,建立了构网型并网逆变器的详细模型,复现了强电网下构网型并网逆变器的失稳现象并采用参与因子分析了不同参数下的失稳问题,利用改进型的IEEE 4节点三相平衡电网系统为算例并借助Matlab/Simulink进行仿真,通过实验得出以下结论。
(1)本文提出的构网型并网逆变器状态空间模型可以有效分析强电网下和控制器参数发生改变情况下系统的稳定性问题。
(2)构网型并网逆变器应用于强电网下会导致系统趋于不稳定状态,其临界短路比为2.01。
(3)增加下垂控制增益或减小电压环控制增益都不利于构网型并网逆变器系统的稳定。
