可再生能源富集区域计及条件风险价值的储能优化规划

朱 瑾， 程 瑜

(华北电力大学 电气与电子工程学院，北京 102206)

0 引 言

加快清洁能源替代,大力发展风电、光伏发电等可再生能源已成为国际社会应对气候变化、实现我国双碳目标的广泛共识[1]。但新能源发电具有随机波动性,给新型电力系统的运行和规划带来了一系列的新挑战[2,3]。尤其是由电网调峰容量不足[4]以及系统网架结构受限[5]所导致的新能源富集地区新能源弃能问题已成为新型电力系统建设关注的焦点。优化规划储能系统,实现储能与可再生能源发电、电网、负荷需求协调配合是新型电力系统建设的必由之路[6]。

目前,储能配置与可再生能源发电协调的研究主要集中在利用储能提高可再生能源可调度性[7],平抑其出力波动[8-10]、减小其预测误差[11]等方面。在大规模可再生能源汇集外送的背景下,优化储能与网架外送断面的协同能力是提升可再生能源消纳的关键策略[12,13],但源、荷双侧波动性也给储能规划带来了更大的风险。文献[12]利用储能提高新能源厂站汇集处的风电外送能力,但未计及网架结构的影响,默认储能与新能源厂站共址。文献[13]计及储能配置对分区外送断面的影响,并基于全年时序生产模拟进行储能规划,但由于涉及长时间尺度,模型求解易陷入维数灾难中,降低了模型的求解效率。文献[14-15]基于不确定性优化规划理论,分别采用场景分析法[14]及机会约束[15]的方式处理可再生能源出力的不确定性。

上述方法在储能规划模型中考虑了可再生能源不确定性的影响,但缺乏对不确定性下规划方案风险的直观量化度量。文献[16-17]分别在微电网及虚拟电厂的电源容量配置规划中引入CVaR (Conditional value-at-risk,CVaR)理论,度量电源规划过程中由于可再生能源出力、市场电价等不确定性因素影响所导致的风险损失。储能规划同样面临源、荷双侧随机因素引起的风险问题,有必要在储能规划中融入风险度量,以实现对规划决策时的风险偏好及风险损失的量化管理,以提高储能配置方案对规划期内的极端场景的适应性。

综上,本文针对可再生能源汇聚外送网络进行储能配置优化,通过CVaR度量可再生能源出力、负荷资源不确定性给储能规划及运行带来的风险,以系统净成本和风险成本最小为目标函数,构建考虑条件风险价值的储能优化配置模型。同时针对储能规划模型的求解效率问题,采用K-MILP聚类算法在储能规划典型场景缩减时保留极端场景,并基于场景法对模型中的CVaR度量项进行线性化,转化含CVaR的储能随机规划模型为混合整数线性规划(Mixed integer linear programming,MILP)模型,便于直接采用商用化的线性规划求解器进行求解。

1 储能投资的VaR和CVaR计算

规模化可再生能源接入后,源、荷双侧波动给电力系统的规划及运行带来了更多的不确定因素。在此背景下,亟需对储能规划过程中可再生能源出力、负荷带来的不确定性因素进行量化。为进一步对储能投资过程中由于不确定性带来的风险进行衡量,本文采用CVaR风险度量工具对可再生能源及负荷波动性给可再生能源富集地区的储能建设及运行带来的风险进行量化。

风险价值(Value-at-Risk,VaR)、条件风险价值是广泛应用于金融市场管理的风险度量工具。针对储能投资的VaR的含义是:在给定置信水平下,系统投资运行净成本最坏的预期损失,即系统投资运行净成本损失不超过VaR的概率为给定的置信水平[17]。VaR可以通过调整置信水平对风险进行调控,但其不满足齐次可加性,不属于一致性风险度量,因此它无法描述损失超过此值的尾部情况。CVaR是对VaR的一种改进,它可以有效克服VaR的上述缺陷,能够有效捕捉损失的尾部信息,比VaR 更能体现投资组合的潜在风险,是一种风险管理中更为合理有效的风险计量方法[17],将VaR和CVaR结合起来可以更好地进行风险度量。针对本文中储能投资的CVaR的含义是:在一定置信水平上,系统投资运行净成本超过VaR的条件均值。

传统意义上,VaR和CVaR是对于损失函数的一种风险度量,本文考虑可再生能源出力及负荷不确定给储能规划及运行带来的风险也是一种损失函数的风险度量,通过引入风险度量项,可以合理权衡电网投资配置储能过程中的风险和收益。

设f(x,y)为损失函数,本文中表示确定性优化模型的目标函数,即受储能投资影响的系统净成本;x为决策变量,即储能的配置布点、容量和功率;y为随机变量,如可再生能源出力和负荷,假设ρ(y)为y的可再生能源出力的概率密度函数,则风险度量函数f(x,y)不大于边界值α的分布函数为

(1)

对于给定的置信度β,VaR可由下式得到:

VVaRβ=min{α∈R:φ(x,a)≥β}

(2)

对于给定的置信度β,CVaR可由下式得到:

(3)

式中:VCVaRβ为置信度β下,储能建设及运行的CVaR值。

由于VVaRβ(x)解析式难以求出,因此推导出变换函数Fβ(x,α)以求得CVaR[17]:

(4)

式中:[f(x,y)-α]+表示max{f(x,y)-α,0}。

α即为VaR的值。由于ρ(y)解析式难以求出,本文采用场景分析法处理可再生能源出力及负荷的不确定性,为精细化分析系统应对尾部风险的能力,构建计及时空相关性且对稀疏离群点具有鲁棒性的不确定性集合w。变换函数Fβ(x,α)可用以下估计式来计算:

[f(x,ws)-α]+

(5)

2 基于K-MILP场景聚类筛选的含CVaR的储能优化规划模型

面向高比例可再生能源外送系统,储能规划将面临更大风险,为体现投资过程中的极端场景尾部风险,采用CVaR进行风险度量。规划过程中为了保证计算的可处理性,需要进行场景缩减,在有限的场景下解决规划问题,同时针对尾部风险的兼顾需求,提出K-MILP场景聚类算法,保留样本集群中最具代表性的典型场景以及较为极端的少数场景。基于K-MILP场景聚类筛选的含风险度量的储能优化规划模型的基本框架如图1所示。

图1 储能优化配置基本框架Fig. 1 Basic framework of energy storage optimization configuration

2.1 基于K-MILP算法的储能规划场景聚类筛选

针对可再生能源出力及负荷的不确定性带来的随机优化问题,场景分析是一种有效方法[18]。本文涉及从大规模可再生能源出力及负荷场景中较为准确地提取原始场景数据变化特征,为达到有效缩减场景数量的目的,考虑以可再生能源-负荷净出力曲线为聚类样本,采用改进的K-medoids算法[19]即K-MILP算法[20]进行场景聚类。K-MILP算法可以同时筛选典型场景和极端场景天数,相比于K-medoids算法,可以更好的保留场景的极端特性,有利于提高风险度量的精度。K-MILP算法从簇中选取一个点作为质心,以簇内各点到质心欧氏距离总和最小作为目标,如式(6):

(6)

式中:Nd为样本数目;ap,q为0-1变量,若样本q能用样本p进行表示,则ap,q=1,否则ap,q=0;dp,q代表样本p和样本q间的欧式距离,计算公式如式(7):

(7)

式中:Nc为样本包含的时段数;c为时间序号;xc,p、xc,q分别为样本p、样本q在时刻c的数值。

K- MILP聚类过程中需满足以下约束条件:

(8)

ap,q≤bp,∀p,q∈{1,…,Nd}

(9)

(10)

(11)

式中:bp为0-1变量,若样本p为簇的代表,则bp=1,否则bp=0;Nk为总聚类数目,即簇的数量;Next为极端样本数;约束条件(8)限制样本q至多有一个簇与之对应,相比于传统K-medoids算法进行了松弛,允许典型场景聚类过程中自动排除极端样本,不再要求每个样本都与一个典型的样本相关联;约束条件(9)限制当样本p不是簇的代表时ap,q恒为0;约束条件(10)保证了簇的数量为给定值Nk;约束条件(11)避免所有的样本都被归为极端样本。

上述聚类过程得到的是全系统净出力典型场景曲线,但规模化可再生能源汇聚外送地区涉及多个可再生能源机组与多个负荷如何组合以形成典型场景的问题。本文根据K-MILP聚类算法得到各类场景对应的日期,提取出该日期下各台可再生能源机组以及各个负荷的出力曲线,形成规划场景集w。

2.2 考虑CVaR的储能配置目标函数

考虑投资风险的储能容量优化配置的目标是在满足各种约束条件的前提下,提高含可再生能源系统的外送通道利用率,并充分利用可再生能源,使得储能投资影响的系统净成本及风险成本最小,其目标函数主要包括系统成本和风险度量项两部分,具体形式如下:

(12)

其中:

Foper=Coper+Cdeal+Closs-Cout

(13)

式中:目标函数第一部分为受储能投资影响的系统净成本,第二部分为风险成本,为FCVaR与L的乘积。xh为储能h是否建设的0-1决策变量,xh为1时表示储能h建设,为0时不建设;Eh、Ph分别为待建储能h的额定容量及额定功率;Fs为储能设备的总投资运维成本;Foper为系统的运行成本,包括常规机组发电费用Coper、常规机组发电产生的环境处理费用Cdeal、失负荷费用即损失的售电收益Closs及外送电收益Cout;FCVaR为CVaR的值,用来衡量可再生能源、负荷不确定性给系统净成本带来的风险;L为风险厌恶系数。目标函数中涉及的各成本项计算方法见式(14)～(21)。

(14)

(15)

(16)

(17)

(18)

(19)

(20)

zs=[f(x,y)-α]+=[(Fs+Foper)-α]+

(21)

2.3 考虑CVaR的储能配置约束条件

考虑投资风险的储能容量优化模型的约束条件包括系统运行约束、机组运行约束、负荷运行约束、储能运行约束和CVaR风险约束。对于所有规划场景s,模型均需满足约束条件式(22)～(34)。

2.3.1 系统运行约束

系统运行约束包括系统静态潮流方程约束式(22)～式(23)、支路潮流约束式(24)及功率平衡约束式(25)。

(22)

(23)

(24)

(25)

2.3.2 机组运行约束

机组运行约束包括常规机组运行约束式(26)～式(27)、可再生能源机组运行约束式(28)。

(26)

(27)

(28)

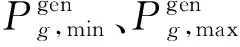
2.3.3 负荷运行约束

负荷约束包括向外部负荷供电的外送电约束式(29)及向内部负荷供电的本地负荷约束式(30)。

(29)

(30)

2.3.4 储能运行约束

储能运行约束主要包括储能的荷电状态约束式(31)、充放电功率上限约束式(32)以及充放电状态约束式(33)。

(31)

(32)

(33)

2.3.5 CVaR风险约束

为了便于计算,可将辅助变量zs松弛为以下两个不等式,从而将CVaR转化为线性问题进行优化求解:

(34)

上述基于K-MILP算法的场景聚类模型以及含风险度量的储能优化规划模型均为MILP模型,可调用MATLAB中的Gurobi求解器进行模型求解。

3 算例分析

3.1 系统参数

某风电富集区域的网架如图2所示,风电装机达到1 750 MW。区域内共有三个主要的风电汇集区:其中汇集区1连接5、19节点的风电;汇集区2连接8、9、10节点的风电;汇集区3连接14、15、16节点的风电;节点 5、8、14分别连接有三条外送通道;节点11、25有接入常规机组。各节点接入的电源装机容量见表1。储能配置的待选节点集合为{2、3、4、5、6、7、8、13、14、19,26}。算例地区风电、负荷年时序曲线见图3。

表1 电源装机容量数据

图2 算例地区网架结构图Fig. 2 Grid structure diagram of calculation example area

图3 风电、负荷年变化曲线Fig. 3 Annual variation curve of wind power and load

设定置信度水平β取90%,风险厌恶系数L取1,化石能源机组发电的环境治理费用为110元/MW·h,以外送通道受电地区的电价为标准,设外送电价为480元/MW·h,常规机组发电价格为372元/MW·h,电网分时电价见表2。储能设备主要考虑电池储能系统( Battery energy storage system,BESS) ,BESS的投资费用及其他运行维护参数如表3所示。外送通道输送容量如表4所示。

表2 电网分时电价

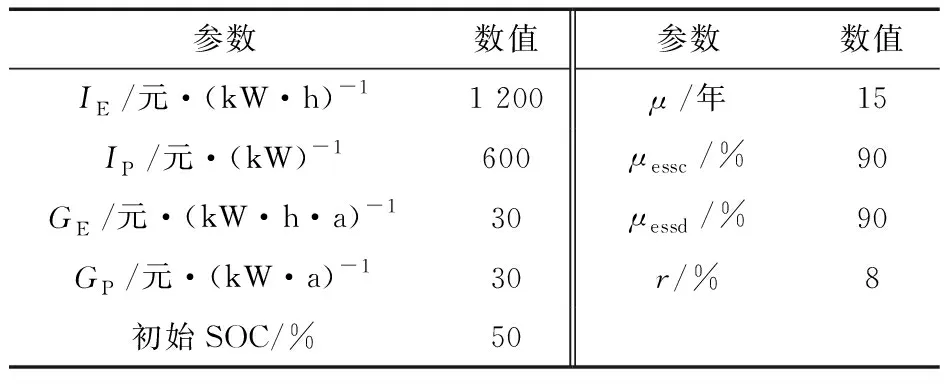
表3 BESS参数

表4 外送通道分布数据

3.2 算例结果与分析

3.2.1 场景聚类结果分析

根据图3中算例地区8 760 h风电出力、负荷数据形成净出力曲线样本,利用2.1节所述的K-MILP场景聚类方法最终聚类筛选出10类风、荷净出力的典型场景。典型场景风、荷净出力曲线见图4,各类场景出现概率见表5。

图4 典型场景风荷净出力曲线Fig. 4 Judgment index value

表5 典型场景概率

3.2.2 BESS规划结果分析

根据2.2节建立的考虑条件风险价值的储能优化规划模型,求解决策储能容量及功率配置结果如表6所示。通过分析表6可知,储能最终布点在了8,14,19节点,这三个节点分别位于3个汇集区内,对应缓解外送通道输送容量对可再生能源消纳水平的限制;其中外送通道2和3的输送容量相对较小,对应在节点8和14优化配置的储能容量相对较大。

将上述储能优化配置方案下的含储系统与不含储能的原始系统的各项经济指标折算到日进行对比,详见表7。可见,含储系统和原始系统的全场景加权后的系统净成本相当,含储系统中尽管系统增加了储能投资,但减少了常规机组的发电成本及环境处理费用,减少了系统失负荷成本,增加了系统外送电收益;同时,CVaR关注对极端场景的风险规避,投入储能后系统风险成本为720.57万元,相比于原始系统有所降低。含储系统中虽然增加了一定的储能投资费用,但带来了相应的运行效益及环境效益,并对风险成本进行了调控。

表7 不同情景下的经济指标

3.2.3 典型场景下的系统运行结果分析

为节省篇幅,集中分析配置储能后对于外送通道及弃风率的改善情况,选取出现概率较大的场景6作为典型日进行分析。其中,含储系统与原始场景在典型日下的风电外送总量情况如图5所示,典型日内含储系统相比于原始系统各项运行指标变化情况见表8。

图5 典型日内外送通道送出情况Fig. 5 Transmission channels delivery conditions of typical day

表8 典型日内不同情景下运行指标变化量

通过图5对典型日外送通道送出情况进行分析可知,配置储能后各条外送线路的外送电量相较于基础场景均有所提升,其中,外送通道2及外送通道3处由于布有储能,相较于外送通道1的外送电量提升较为显著,分别达到了2%及4.69%。引入BESS后,可以有效提高风电的消纳及风电外送水平。

通过分析表8可知,配置储能后,火电机组发电量减少,失负荷情况得到缓解,外送电量有所提高,但仍然存在弃风现象。该含储系统中整体储能配置容量为可再生能源装机容量的7.4%,占比不到10%。这说明虽然BESS可减少弃风、提高风电外送,但当前储能的投资造价较高,仅通过表8中运行指标提供的经济驱动力不足以配置足够的储能实现可再生能源全消纳,尤其是难以满足极端场景下的可再生能源消纳水平,盲目追求全场景的运行效益可能会丧失储能配置的经济性。因此有必要在规划模型中考虑一定置信度水平下运行效益的改善,经济提升可再生能源消纳水平。

3.2.4 不同置信度下尾部风险及储能配置结果的灵敏度分析

不同的投资主体具有不同的风险偏好程度,所选取的置信水平与决策者的风险厌恶水平密切相关。投资者可通过调整置信度来改变对于尾部风险的承受情况,置信度越高,风险厌恶水平越高,对于风险的规避性越强。表9反映了不同置信度水平时储能配置结果与极端场景下的尾部风险成本。

表9 储能配置点处的各项参数值

通过表9可知,当设置的置信水平较低时,系统的尾部风险成本较高。为增强系统应对风险的能力,需提升置信水平,此时投资者倾向于投入更多的储能设备成本以规避储能投资及运行过程中由于各种不确定性因素带来的风险,这是由于置信度水平上升,投资者对于风险的厌恶水平增加,考虑的不确定性因素越多,系统运行过程中的安全稳定性要求越高,所需的灵活性越大,此时尾部场景成本相应减少,系统投资运行过程中的尾部风险得到有效控制,但储能投资成本增加。进一步分析储能规划特点可发现,随着置信水平的提升,储能容量、功率均有所增加,并倾向于分散布点,故储能规划策略需协同储能容量及空间布点之间的关系,以尽可能少的投资降低系统的尾部风险。实际决策过程中,投资者应根据自身的需求,确定合适的置信水平,即可限制储能规划及运行过程中面临的投资风险。

4 结 论

本文考虑了大规模可再生能源接入电网以及负荷的不确定性给电网侧储能投资带来的风险,通过 K-MILP聚类筛选出保留风、荷极端特性的典型场景集,采用CVaR度量上述不确定性带来的风险,兼顾本地消纳及可再生能源外送,建立一种计及条件风险价值的储能配置优化模型,并探讨了储能投资规模与置信水平之间的关系。通过仿真分析得到结果如下:

(1)针对可再生能源汇聚外送区域,储能布点更倾向于可再生能源接入点以及外送通道连接节点,提高可再生能源通道利用率、改善由于线路阻塞导致的失负荷情况,即可再生能源汇集区、外送通道空间分布协同作用影响储能空间布点。

(2)在模型中计及风险度量,有利于规划过程中的风险管控。CVaR的引入能够有效衡量电网规划中面临的风险,系统储能投资成本与置信度水平呈正比,尾部风险与置信度水平呈反比。为提高规划方案应对风险的适应性,针对多通道外送可再生能源富集区域,储能规划策略可配合储能容量的提升及更加分散的空间布点协同作用,平衡经济性和鲁棒性,降低储能投资面临的尾部风险。

综上,本文面向可再生能源汇聚外送地区建立了含风险度量的储能优化模型,该模型考虑了一定置信度水平以外的尾部风险,反映规划过程中的随机性,有利于更好的权衡储能投资过程中的经济性与风险性。后续可在本模型基础上融合外送线路及火电机组扩建容量的决策进行协同规划,深入探讨不同设备的容量配比对于风险的适应能力。