指向高阶思维的初中数学深度教学

王雅娅

[摘 要] 在新课改的推动下，开展深度教学已成为初中数学教学发展的必然趋势.在实际教学中，学生的“学”不能局限于知识的理解和记忆，也要从应用、分析、综合、评价等层次上下功夫，重视揭示问题的本质，提炼数学思想方法，促进学生数学高阶思维的发展.

[关键词]深度教学；本质；高阶思维

基金项目：重庆市教育科学“十四五”规划2023年度一般课题“区域推进家校社合作育人的机制与路径研究”（S23YG1100031）.

深度学习是一种基于高阶思维发展的理性学习，具有一定的批判性、整合性，突出迁移应用和主动建构.浅层学习关注的是学习结果，强调知识的理解与记忆，是一种被动的学习方式，不利于学生长远发展.而深度学习关注的是学生的学习过程，侧重于知识的应用、分析、综合、评价，是主动思考、主动建构的过程.教师作为课堂教学的组织者，应将关注学习结果向关注学习过程及过程评价转变，在教学中强调自主探究和合作学习，重视学生批判性、发散性思维方式的培养，从而化被动为主动，让学生学会思考、学会学习.

培养高阶思维就需要教师改变传统的以讲授为主的教学方式，要提供时间和空间让学生主动参与到课堂学习中来，激发学生理解数学知识，探索问题本质的思维兴趣，让学生成为课堂的主体，促进学生高阶思维的发展.为了实现这一目标，教师在教学中可以设计一些阶梯型、体验型、反思型问题，以此在问题的探索中触发高阶思维，实现深度教学.

创设阶梯型问题，促进知识深化

若想让学生能够深刻地理解知识，并能灵活应用知识解决问题，教师应带领学生参与知识的探究过程，以此通过亲身经历获得真实的体验和感悟，促成深层次的理解.在实际教学中，教师应遵循学生的认知规律，通过创设阶梯型问题引导学生亲历知识发生、发展和应用等过程，让学生知道知识从哪里来，又将到哪里去，以此促进知识的深化，提高数学应用水平，发展综合素养.

案例1 “字母表示数”教学片段

为了让学生体验字母表示数的必要性和优越性，教师设计了如下问题.

（1）图1是由同样大小的小正方形拼成的正方形，说一说，图1各图中分别有几个正方形.

（2）前面一個图形比后面的图形少几个小正方形？如果按照这个方式继续拼下去，第4个图形有几个小正方形？它比前一个图形多几个小正方形？

（3）第2024个图形比第2023个图形多几个小正方形？

（4）结合以上研究经验，你能用数学方法表述其中的规律吗？

前面两个问题较为简单，学生通过“数一数”“拼一拼”就能轻松地给出答案.这样通过简单的、直观的问题的解决，让学生感知丰富.随着图形的增多，通过“数”“拼”等很难解决问题，由此诱发学生主动探寻蕴含其中的规律.重新观察图形不难发现，后一个图形比前一个图形增加了一行一列，如第1个图形是1行1列，第2个图形是2行2列，第3个图形是3行3列，可见增加的行、列刚好与序号一致，这样除去行与列交汇处重复的小正方形，可以轻松地判断第2024个图形比第2023个图形多（2×2024-1）个小正方形.这样通过经历问题（3）的深入探究，蕴含其中的规律已经显现，于是学生自然地联想用字母n代替序号，得到第n个图形比第（n-1）个图形多（2n-1）个小正方形.通过阶梯型问题的解决，学生的思维螺旋上升，这不仅帮助学生突破了字母仅表示实际问题中的未知数的局限，而且实现了一次从形到数的建模，促进学生高阶思维的发展.

评析 从简单的、熟悉的问题入手，逐渐引导学生挖掘蕴含其中的规律，让学生体会用字母替代文字来描述规律更加简洁明了，用字母表示数的优越性和必要性.这样从传授知识转化为自主探究知识，学生的思维在问题的解决中不知不觉地得到发展.

创设体验型问题，激发数学思维

由于体验式教学给学生提供了更广阔的空间，促进学生主体性的激发和基本活动经验的积累，因此其已成为初中数学教学方式之一.在教学中，教师可以结合教学实际设计一些体验型问题，让学生在动手实践中发现、提出、分析并解决问题，以此通过亲历探究过程活动真实地感知数学，帮助学生深刻地理解知识，获得持续发展的学习能力.

案例2 “角”的教学片段

为了让学生更好地体验“角”、感悟“角”，教师让学生以小组为单位，开展“拼图大作战”.

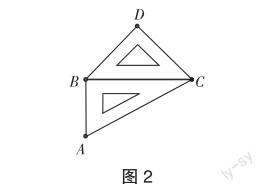
比赛规则：如图2，用一幅三角板拼出小于180°的角，如∠ACD=∠ACB+∠BCD=75°，每拼出一幅合格的图形得1分，重复图形不得分.

比赛时间：5分钟.

评价方式：小组互评，并计算各组总分.

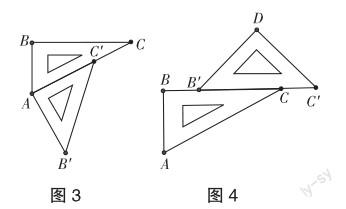
活动给出后，学生积极动手操作.学生边操作、边思考、边交流，最后达成共识：若想得到合格的图形，就需要将一幅三角板的边重合在一起.找到解决问题的根本后，学生拼出了多种符合条件的图形.通过动手拼让学生直观感知角是由一个顶点和两条边拼成的，这样不仅使角的概念变得更加直观、形象、具体，而且为后续角的计算打下了坚实的基础.活动中，教师创造机会让学生阐述自己的设计，让学生充分体验解决方法的多样性，拓宽学生的视野.通过有效的合作交流，学生给出了许多有创意的作品，如有的学生拼出图3所示的图形，然后提出计算∠BCC的度数；有的学生设计图4所示的图形，并提出计算∠BBD的度数，等等.以上设计打破了最初“角的顶点一定是两块三角板重合点”的局限.在有效的动手操作中，学生充分享受学习数学的乐趣.

評析 合作与竞争是当下新型人才应具有的一种基本素养.在教学中，教师以小组为单位，巧妙地设计竞争活动，既能调动学生参与活动的积极性，又能激发学生的合作意识，使课堂呈现别样精彩.实践证明，带有竞争性的体验式活动更能激发学生主动思考，使学生真正地做到“做中学”“学中思”，促成深度学习.活动中，教师预留充足的时间让学生去交流、去表达，以此让学生在“做数学”的过程中学会思考、学会表达，让学生的思维逐渐走向高阶.

创设合作性问题，提高合作能力

数学课堂不是教师的独角戏，也不是个别学优生的修炼场，而是师生共同合作与交流的舞台.新时代背景下，合作能力已成为学生应具备的适应时代发展的关键能力.在教学中，教师要充分发挥个体差异的优势，让学生通过合作各取所长.当然，为了确保合作学习顺利开展，教师要依据学生的认知水平、性格特征、组织能力等科学分组，并按照学情创设探究活动.在活动过程中，学生的实践能力及合作意识等多方面素养得到协调发展.

案例3 探索“余角”的概念

活动要求：请先阅读课本中有关余角的内容，然后以小组为单位完成问题1到问题3，并换位思考：如果你是老师，你想如何提醒学生正确地理解余角的概念.

分组情况：每个小组6人，每组分为A，B，C三级（C级表示能力相对较弱，B级表示能力一般，A级表示能力相对较强）.

问题1 （1）请测量图5中的∠α和∠β，并结合测量结果说一说∠α和∠β存在怎样的特殊关系.（精确到度）

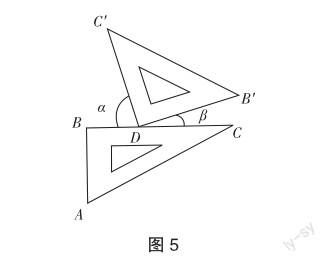
（2）若点D保持不动，转动△CDB，试猜想∠α与∠β之间的特殊关系是否依然成立.

（3）你能用已有知识证明（2）中的猜想吗？

问题2 如果 ，那么这两个角互为余角.

问题3 如果让你画两个互余的角，你会吗？

问题4 判断下列说法是否正确.若不正确，请说明理由.

（1）如图6，B是直线CD上一点，且∠ABD=90°，则∠ABE与∠EBD互为余角.

（2）如图7，∠AOC=∠BOD= 90°，则∠AOB与∠BOC，∠BOC与∠COD互为余角.

（3）如图8，∠1=25°，∠2=65°，则∠1与∠2互为余角.

在教学中，学生以小组为单位共同学习，教师巡视，当组内出现难以解决的问题时，教师及时进行启发和指导.下面呈现某小组合作学习过程.

组长：谁来说一说自己的测量结果？（组长点名让基础较弱的学生回答）

生1：∠α=20°，∠β=70°.

组长：大家的测量结果都一样吗？（学生点头表示一致）

组长：那你继续说一说，你发现了什么特殊的关系？转动后有何变化呢？

生1：两个角的度数加起来正好是90°，转动后该特殊关系应该是不变的，不过怎么证明我还没想好.

组长：不错，以上两个问题的答案都对.谁来说一说如何证明这一猜想？（组长将目光投向B级学生）

生2：因为∠α+∠β+CDB=180°，又∠CDB=90°，所以∠α+∠β= 90°.（生1恍然大悟）

组长：问题（2）比较简单，教材上就有，大家写的都没有问题，我们就不再讨论了，现在我们继续看问题（3）.请大家分别呈现自己的作品，我们一起观察、探讨一下.

组员分别呈现作品，然后进行组内评价，以此进一步深化对余角概念的理解.紧接着学生又主动探讨问题（4），各抒己见，气氛活跃.对于问题（1）和问题（2），学生很快形成了统一意见；对于问题（3），学生产生了分歧，在教师的启发和指导下形成正确的认识：两个角只要满足相加之和为90°即互为余角，它们不一定有公共顶点，也不一定在同一张图上.在教师的指导下，学生通过有效合作认清了两角互余的数学本质，发展了合作能力.

评析 小组合作并不是个别学生的独角戏，合作中组长要充分发挥其组织者的作用，根据问题的难易程度合理安排学生作答，要让每一个学生都能参与其中.这样通过合作，学生相互启发、相互理解、相互扶持，以此都能有所成长.当然，放手合作并不意味着教师撒手不管，而是在学生产生困惑时给予点拨，以此增强学生学习信心，培养学生乐学、善学的学习品质，发展学生的高阶思维.

创设反思型问题，引发高阶思维

在日常教学中，教师应重视引导学生自我反思，以此逐渐提升学生的反思意识和反思能力.在教学中，多数教师有这样的困惑：有些题明明重点讲解并练习过，但是考试时学生还是会出错.其实出现这种现象的主要原因之一就是师生忽视了解后反思.解题时，很多学生仅仅追求结果，并未对思想方法、解题能力、出错的原因进行有效反思，对题目的认识停留于表面，题目略加变动就犯错.因此，解题后，教师要提供时间给学生自我反思，并鼓励学生尝试从不同视角探究问题，以此弄清问题的来龙去脉，有效规避错误的再次发生.

总之，深度教学是课堂教学的必然趋势，而这里的“深”不是加深教学内容的难度，而是深化教学目标，引发深度思考，让学生掌握问题本质，发展高阶思维，培养核心素养.