探究性学习在初中数学教学中的应用研究

谷周波

[摘 要] 探究性学习是一种积极主动的思维活动，学生在探究过程中不仅能有效提高逻辑思维能力，还能不断积累探究经验，为形成终身可持续性发展的探究能力奠定基础.文章以“三角形的中位线”的教学为例，具体从“情境导入，初露端倪”“几何推理，步入正轨”“借助图形，引发思辨”“逐层深入，训练思维”四个方面谈谈如何科学合理地设计教学活动，帮助学生积累探究经验.

[关键词]探究；教学设计；中位线

基金项目：江苏省教育科学“十四五”规划2021年度初中专项课题“指向深度学习的初中数学单元整体教学实践研究”（Ec/2021/39）.

《义务教育数学课程标准（2022年版）》（简称“新课标”）提出要将数学探究经验的积累与建模活动作为课堂教学的主线，贯穿整个教学过程[1].这对教师的教学设计也提出了更高的要求.在实际教学中，探究活动经验的积累常常受诸多因素的影响，教材所配备的探究资源未必与学情相匹配，这就要求教师灵活整合教材资源与学情合理设计教学，提高学生探究经验积累的成效.

情境导入，初露端倪

初中阶段的学生已经有了一定的生活阅历，积累了一定的学习经验.在课堂导入时，教师可紧贴学生的认知水平，紧扣教学内容所传递的数学思想方法与内涵等，通过通俗易懂的方式实施情境导入，为一节课顺利进行做铺垫.

三角形的中位线是在学生对三角形与四边形有所了解后进行的教学，大部分教材都是以旋转、剪拼或重叠等方式来验证一些线段、角之间的关系.顺着教材的思路进行教学，操作简便，学生也容易理解，但在实际操作过程中，有学生提出以下几个问题：①沿着三角形两边中点连线进行剪切是怎么想到的呢？②这种剪切方法与之前所学的知识有什么关系？

为解开学生的疑惑，教师在教学设计时，特地设计了如下充满数学味的导入情境.

要求学生从认知储备中提取已知的关于三角形的线段，学生很快就整理出三角形的三条边、角平分线、高以及中线.在此基础上，教师提出以下问题，并引导学生回答.

问题1 如图1，在△ABC中，已知D为AB的中点，连接CD，可以获得什么结论？

生1：△ACD和△BCD的面积相等.

问题2 如图2，若E为AC的中点，连接ED又能获得什么结论呢？

生2：ED为△ACD的中线，因此△AED与△DEC的面积相等.

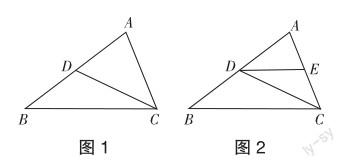
师：非常好！若将图2中的线段CD去掉，有什么发现？

生3：如图3，△AED的面积与四边形CEDB的面积之比为1∶3.

师：非常好！以上内容为本节课我们即将探索的主题“三角形的中位线”的基础.现在请大家来看三角形中位线的概念.（多媒体直接展示，要求学生分组合作讨论其可能存在的性质）

数学是一门系统性的学科，知识与知识之间有着一定的联系，旧知为新知的基础，新知又是旧知的延伸.因此，教师在导入新知时，应致力于将新知与学生原有的认知经验和结构建立一定的联系，通过一些铺垫性问题的设置为新知学习搭建“脚手架”，让学生顺利实现新旧知识的衔接，优化认知结构.

本节课的情境导入，教师以问题串的形式，带领学生从“三角形中线平分面积”这一知识点出发，揭露了三角形两边中点的连线可将原三角形分割成面积比为1∶3的两个图形.数学的思维自然而然地从三角形“中线”转化到“中位线”，不仅顺利完成了概念的导入，还为中位线性质的猜想奠定了基础.这种低起点、小步子、高观点的巧妙设计，符合学生的认知规律，让学生的探究活动有据可循、层次分明、初露端倪.

几何推理，步入正轨

定理是几何体系的基础与核心，也是学生认识与解决几何问题的依据.基于几何定理本身来说，所有定理都由严谨的推理论证而来，具有典型性与抽象性，且定理的求證过程也极具代表性，是积累探究经验的主要渠道[2].

例如本节课，对三角形中位线定理的证明，可从以下思路出发：

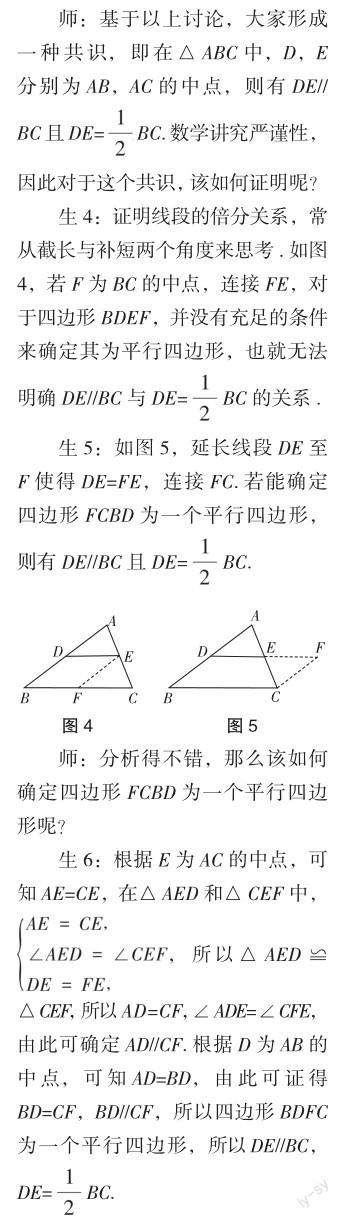
师：非常好！思路清晰、条理清楚，生6构造一对全等三角形作为思维的“切入点”，顺利推导出相应的结论.现在请大家分析一下，是否存在其他方法可以证明四边形FCBD为平行四边形呢？

师：这种跨越三角形全等的证明方法，优化了解题思路，让证明过程变得更加简便，值得推广.

初中数学教学中的问题探究是指带领学生基于数学的视角应用数学眼光思考与解决问题，形成解决问题的能力，积累探究经验，增强应用意识的过程.因此，教师在课堂中应给予学生充足的思考与探索时间，让学生有更多操作与实践的机会，为积累探究经验奠定基础.

中位线定理的探究主要从如下几点着手：①利用三角形全等来求证角度与线段分别相等，得到平行或倍分关系；②结合平行四边形的性质，证明平行与倍分关系.这两种方法作为几何论证最常用的方法，属于学生必备技能.因此，课堂探究活动需围绕这两种方法逐层深入地进行，以促进学生思考，帮助学生积累解决几何问题的基本活动经验.

借助图形，引发思辨

几何定理教学不仅要引导发现、理解并掌握定理，更要指导学生应用定理解决实际问题.当学生顺利完成定理的推导后，为了巩固学生对知识的掌握与应用，教师要通过相应的习题帮助学生厘清定理的应用过程，获得解题技巧，发展逻辑思维能力.事实证明，借助图形进行解题训练常能有效地揭示知识间的内在联系，让学生感知数学的整体性、条理性与系统性特征，为建构良好的知识脉络奠定基础.

例1 （1）如图7，在△ABC中，已知D，E分别为AB，AC的中点，连接DE，如果BC=4 cm，∠B=40°，求∠ADE的度数以及DE的长度.

（2）如图8，在△ABC中，已知D，E，F分别为AB，AC，BC的中点，分别连接DE，EF，如果△ABC的面积是8 cm2，那么四边形BDEF的面积是多少？

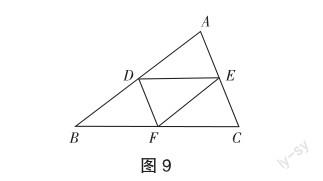
（3）如图9，在△ABC中，已知点D，E，F分别为AB，AC，BC的中点，分别连接DE，EF，DF，如果△ABC的周长是6，那么△DEF的周长是多少？

（学生独立思考并解题，教师巡视，展示学生的结论，此略）

当学生顺利完成解题任务后，教师挑选几个思路清晰、书写过程规范的解法投影（略），并提出以下几个问题：①在图7中，四边形CBDE是什么四边形？②在图8中，△AED与△ECF全等吗？四边形 FBDE是平行四边形吗？③在图9中，四个小三角形全等吗？

画图、读图与识图是几何学习的基础，图形传递出大量的信息是引发联想的关键.解题中，新图形的形成与应用，常能有效开阔学生的视野，优化学生的认知结构，促进学生创新意识的形成与发展.

教师针对以上三个图形所补充的问题，让学生对本节课的教学内容获得了进一步认识.随着对核心知识的提炼与梳理，学生自主将三角形中位线相关的知识罗列在一张网上，形成一个有序化、条理化的整体.乌申斯基认为：组织良好的知识体系是真正的智慧.在教师的引导下，学生将知识进行了纵横沟通，编织出一张层次分明、条理清晰的知识网络，积累了丰富的探究经验.

逐层深入，训练思维

知识的应用是外化的过程，概念的学习最终都要为解题服务，若想更深层次地训练学生的思维，实现学生探究经验的内化，教师要设计与知识相匹配的问题引导学生展开深入思考，让学生在概念的实际应用中进行比较、分析与推理，实现新旧知识的整合与联系.

例2 填空.

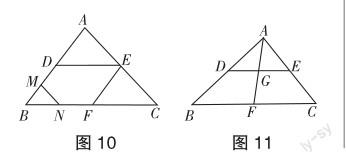
（1）如图10，在△ABC中，已知D，E，F分别为AB，AC，BC的中点，M，N分别是线段DB，BF的中点，若NM=a，则AC= .

（2）如图11，已知AF为△ABC的中线，DE为△ABC的中位线，线段DE与AF相交于点G，AF=5，GF= .

（学生解题，教师巡视，邀请几个学生简单地与大家分享解题方法）

生8：连接图10中的DF，则NM为△DBF的中位线，FD=2NM=2a.同理可知AC=2FD=4a.

师：通过解决这道题发现，适当地添加辅助线能为解题创造出有利条件，谁来分享下第（2）题的解法呢？

概念、定理、法则等的应用是将知识转化为能力的主要途径，经典例题能深化学生对知识的理解程度，形成解题技巧，在思维训练中完善思维品质[3].因此，教师在例题设计或选择时，应基于学生探究经验积累择优而行，让学生通过解题了解知识本质，感受数学学科的魅力，感知解题带来的成就感，让学生从真正意义上喜欢数学探究活动.

总之，探究性学习在数学教学中具有重要意义.在日常教学中，我们应将探究活动与最基础的概念、定理、法则等的学习自然地融合在一起，帮助学生積累探究经验，让学生感知数学学习的乐趣所在，为形成良好的学习能力奠定基础.

参考文献：

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.

[2] 沈木勇.“双减”背景下提升初中数学课堂教学效益的策略[J].中学数学，2022（02）：91-93.

[3] 俞宏毓，朱向阳，顾冷沅.探究教学的设计与改进——以“面积与周长的关系”教学为例[J].数学教育学报，2018，27（01）：68-71.